地鐵車站圍護結構地下連續墻作為橋梁樁基的豎向承載力分析

易瓊

（廣東省交通規劃設計研究院集團股份有限公司，廣州510507）

1 引言

近距離、小凈空、大深度已成為現階段城市地下工程避不開的施工關鍵詞。不斷涌現的高架橋下新建地下工程就是典型案例[1]。若是考慮合建形式將地下工程的圍護結構用作之后的高架橋樁，不僅可以提高工程集約度，還可以減小后續施工難度。其中，地下連續墻豎向承載力大、整體性好，用以代替橋梁樁基具有較高的可行性和工程經濟價值。蔣建平等[2]指出，單片地下連續墻可看成矩形混凝土樁，而相同體積下矩形樁的側面積比圓形樁大，受到的側摩阻力更大，豎向承載力也更大。

然而，地下連續墻在設計時并未從豎向承載力角度進行考慮，要用作高架橋的樁基需要進行另外的計算分析。雖然國際上有一些采用地下連續墻作為建構筑物承重基礎的案例[3]，但國內將地下連續墻作為基礎的工程還比較少，且大多數研究多集中在數值模擬和試驗方面，如張波等[4]和宋章等[5]采用數值方法研究了考慮土芯后的閉合型地下連續墻基礎豎向承載性能，而焦瑩[6]和霍少磊等[7]則結合試驗，探討了單片地下連續墻的豎向承載性狀及承載力。但目前仍缺乏對地下連續墻基礎承重模式和計算方法的研究，故有必要從理論角度分析地下連續墻作為高架橋樁時的受力特點及性能。

因此，本文提出一種計算地下連續墻豎向承載能力的方法，用以分析作為橋梁樁基的地下連續墻受力性能，從而為今后類似工程提供一定參考。

2 工程概況

廣州某地鐵車站擬建于一交叉路口，該路口已有一跨線高架橋規劃中，同時高架橋一側地下已有建成的綜合管廊，在有限空間下地鐵車站布局難以展開。為充分利用路口下方的地下空間，提出將地鐵車站圍護地連墻兼作高架橋樁基的合建方案。

本工程中高架橋樁均設計為端承樁，合建形式采用地下連續墻對單側橋樁的替換。圍護地連墻厚1 m，單幅長6 m；高架橋單個承臺下設4 根樁，每側2 根，樁徑1.6 m。車站圍護結構地下連續墻和高架橋的相互關系見圖1。

圖1 地鐵車站及高架橋相對位置關系圖

替代地連墻及原高架橋樁設計長約35 m，端承樁，樁端嵌入微風化灰巖。周邊地層自上而下分別為：<1-2> 素填土、<4N-2>粉質黏土、<3-2>中粗砂、<5C-1B>粉質黏土、<5C-2>粉質黏土、<9C-2>微風化灰巖。各土層物理力學參數見表1。

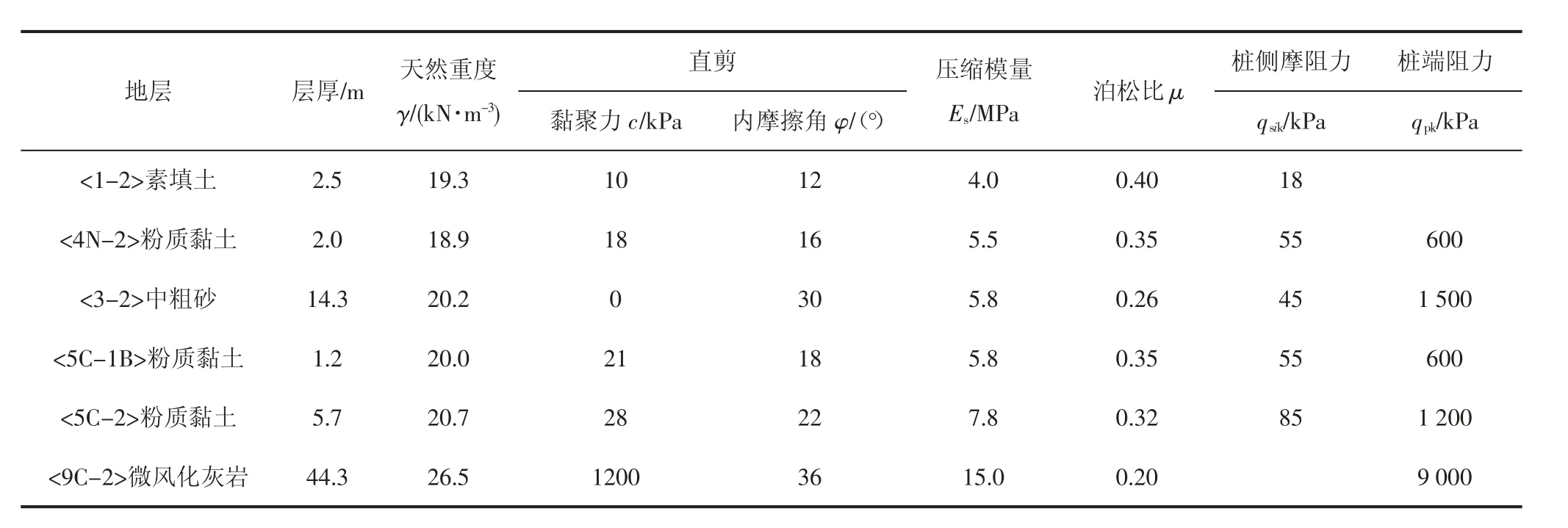
表1 土層的主要物理力學參數

3 理論計算分析

3.1 地下連續墻豎向承載力求解

蔣建平等指出采用俞式增長模型來近似地下連續墻的荷載-沉降曲線的效果較好。針對地下連續墻的荷載-沉降曲線（Q-s 曲線），俞式方程為：

式中，Q 為墻頂豎向荷載，kN；p1為墻頂漸近極限豎向荷載，kN，乘上折減系數0.8[5]可得豎向極限承載力；p2、p3為參數；s 為墻頂沉降，mm。

JGJ 94—2008《建筑樁基技術規范》5.3.9 中規定嵌巖樁的單樁豎向極限承載力Quk如下：

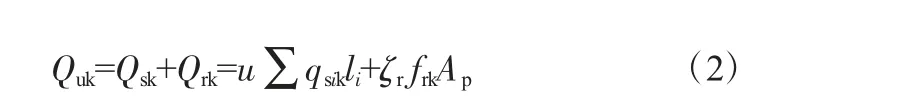
式中，Qsk為土的總極限側阻力，kN；Qrk為嵌巖段總極限阻力，kN；u 為地連墻橫截面周長，m；qsik為樁周第i 層土極限側阻力，kPa；li為樁周第i 層土層高，m；frk為巖石飽和單軸抗壓強度標準值，可用巖層樁端阻力qpk代替；ζr為嵌巖段側阻和端阻綜合系數；Ap為地連墻端部面積，m2。

本工程<9C-2>微風化灰巖frk為20～35 MPa，地連墻嵌巖深徑比hr/d 約為4.5，查表得ζr最高取為1.04。將單幅地連墻尺寸和土層參數代入式（2）得到豎向極限承載力為Quk=74 262 kN。則墻頂漸近極限豎向荷載為p1=Quk/0.8=74 262/0.8=92 827.5 kN。

而根據蔣建平等所總結的6 個工程案例，p2、p3加權平均后分別為1.09 275 和0.677 27，代入式（1）計算得到本工程地連墻的荷載-沉降曲線方程為：

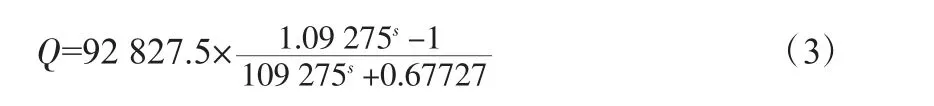
得到本工程的地連墻荷載-沉降（Q-s）曲線如圖2 所示。

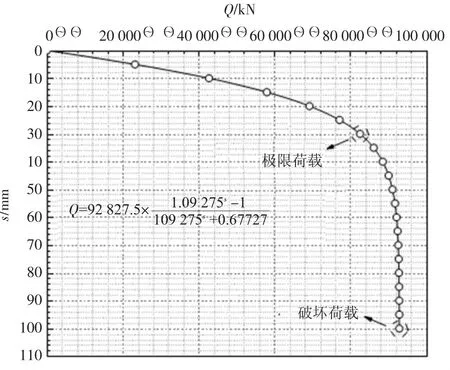
圖2 理論計算所得地下連續墻Q-s 曲線

一般來說，Q-s 曲線明顯向下彎曲的前一級荷載為極限荷載，即極限承載力。故從圖2 中可知，對于該地連墻，豎向極限承載力約為82 500 kN，對應的豎向沉降約為30 mm，考慮折減系數K=2，可取41 250 kN 作為該地連墻的豎向承載力特征值。

3.2 不同初始變形下的地下連續墻豎向承載力

通常對于嵌巖端承時的地連墻，可假定到達豎向承載力極限值時墻端正應力相等。故考慮地連墻初始水平變形，按墻端正應力σ 相等進行替換，可得：

式中，Q 為標準情況下的地連墻頂豎向荷載，kN；Q1為考慮水平變形后的地連墻頂豎向荷載，kN；e 為地連墻發生的水平變形距中軸線的距離，m；Wp為地連墻截面抗彎模量，m3。

式中，L 為地連墻長度，m；t 為地連墻厚度，m。

將式（5）代入式（3）得到：

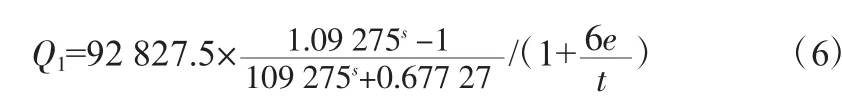
本工程地連墻的厚度為1 m，分別取e=0、0.01 m、0.02 m、0.03 m、0.04 m、0.05 m，代入式（6）得到不同水平變形下的地連墻荷載-沉降曲線如圖3 所示。

從圖3 中可知，對于該地連墻，對應初始水平變形e=0、0.01 m、0.02 m、0.03 m、0.04 m、0.05 m，豎向極限承載力分別約為82 500 kN、81 600 kN、80 800 kN、80 100 kN、79 300 kN、78 500 kN，考慮折減系數K=2 后，豎向承載力特征值分別為41 250 kN、40 800 kN、40 400 kN、40 050 kN、39 650 kN、39 250 kN。

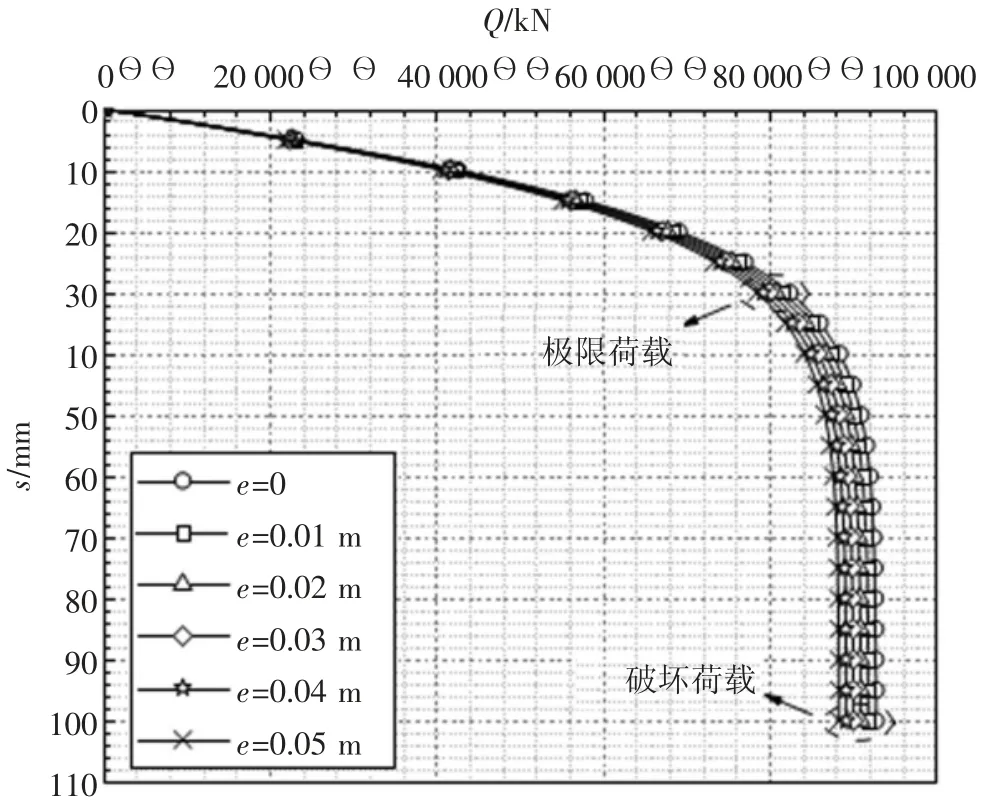
圖3 理論計算所得不同初始水平變形時的地下連續墻Q-s 曲線

可見，即使初始水平變形達到50 mm，豎向承載力特征值也僅減小了約4.8%，幾乎可忽略不計。

4 有限元分析驗證

采用MIDAS/GTS 有限元軟件建立地下連續墻替換單側橋樁后的高架橋墩及樁基豎向加載的數值模型，如圖4 所示。地下連續墻和高架橋的相對位置關系見圖1。整個模型長80 m、寬50 m、高70 m，其中地下連續墻和原橋樁的長度均取為35 m。

圖4 地下連續墻豎向加載數值模型

4.1 地下連續墻豎向承載力對比分析

采用位移法來模擬加載過程，即對地下連續墻施加位移邊界條件，然后求得發生對應位移時的墻頂反力。根據結果繪制地下連續墻的荷載-沉降曲線如圖5 所示，并與理論計算結果進行對比。

圖5 數值模擬所得地下連續墻Q-s 曲線

由圖5 可知，在加載前期，數值與理論曲線變化趨勢基本一致。但在加載后期理論曲線到達陡降點荷載不再繼續增大后，數值曲線的荷載卻還在不斷增大。這是由于基于連續介質力學的有限元無法考慮土體極限破壞后的承載能力下降，因此沉降增加的過程中荷載一直增大，曲線陡降點非常靠后。

于是假定到達極限荷載時對應的沉降以理論計算為準，取為30 mm。此時數值模擬得到的豎向極限承載力為82 500 kN，與理論結果十分接近。

4.2 初始水平變形對地下連續墻豎向承載力影響

在數值模型中依次改變地下連續墻的初始水平變形，然后進行計算，得到不同初始水平變形下的地下連續墻荷載-沉降曲線如圖6 所示。

圖6 數值模擬所得不同初始水平變形時的地下連續墻Q-s 曲線

由圖6 可知，若取豎向沉降30 mm 時對應的荷載作為豎向極限承載力，則數值模擬中對應初始水平變形e=0、0.01 m、0.02 m、0.03 m、0.04 m、0.05 m 的地連墻豎向極限承載力分別約為85 615 kN、85 325 kN、85 536 kN、85 711 kN、85 872 kN、85 991 kN，之間最大僅相差0.78%，其影響幾乎可以忽略不計。

5 結論

本文以某地鐵車站圍護結構與高架橋的合建工程為背景，通過理論和數值手段對替換高架橋樁的地連墻豎向承載力進行研究，得到如下結論。

1）地連墻比同體積的圓形樁剛度大、整體性好、豎向極限承載力大，適合作為豎向承載基礎。

2）基于俞式方程推導出了標準情況下的地下連續墻荷載-沉降方程，求得其豎向極限承載力。

3）推導得到考慮初始水平變形后的地連墻荷載-沉降方程及其豎向極限承載力，更符合地連墻的圍護結構這一特征，便于在實際中應用。

4）經分析，實際允許產生的水平變形對地連墻豎向承載力的影響可以忽略，表明圍護地連墻完全可以作為橋梁樁基繼續發揮豎向承載作用。