融合退化過程和譜分析的接觸網檢修模式優化研究

張鵬強

0 引言

接觸網系統作為高速鐵路牽引供電系統的關鍵設備，具有無備用、結構復雜、易受沖擊等特點，檢修維護工作對保障高鐵系統的安全與效率至關重要[1]。隨著我國高速鐵路建設的快速發展，以周期修為主的維修模式未充分考慮高鐵接觸網系統的結構特點和服役條件，存在耗時長、效率低、工作量大、成本高昂等不足，已不能滿足高鐵接觸網運營維護的需求[2，3]。

依托快速發展的接觸網檢測監測技術，將被動式的周期修改善為主動式的狀態修，對于接觸網系統維護具有重要意義。目前，接觸網檢修優化的研究主要以設備可靠性或設備狀態為中心。前者基本目標是以最小資源消耗保持接觸網設備的可靠性，在一定程度上增強了接觸網系統維修作業的針對性[4，5]。后者將PHM 思想引入接觸網運維領域，根據6C 檢測數據對設備狀態進行預測性診斷，并據此制定維修計劃[6]。但以上思路的研究對象是單一類型的接觸網設備，未能實現對維修資源的全面優化。

本文全面考量影響接觸網系統運行狀態的各類因素并分析其影響程度，建立合理的高速鐵路接觸網系統運行狀態評價體系與退化模型，基于接觸網系統運行狀態制定主動維修策略，并結合譜分析優化計劃修周期，使接觸網系統維修作業更加科學與高效。

1 高速鐵路接觸網系統運行狀態評價模型

1.1 接觸網系統運行狀態評價體系的構建

高速鐵路接觸網狀態評價的目的是將接觸網系統不同層級的多項指標加以綜合得到其穩定度，然后對穩定度進行分析運算，從而對接觸網系統進行整體性評價，確定接觸網運行狀態等級。接觸網系統運行狀態框架主要由3 個層面構成：決策目標是接觸網運行狀態，直接相關的一級指標為可靠性指標、可用性指標和可維修性指標，各一級指標下設相應的二級指標。接觸網運行狀態評價體系如圖1 所示。

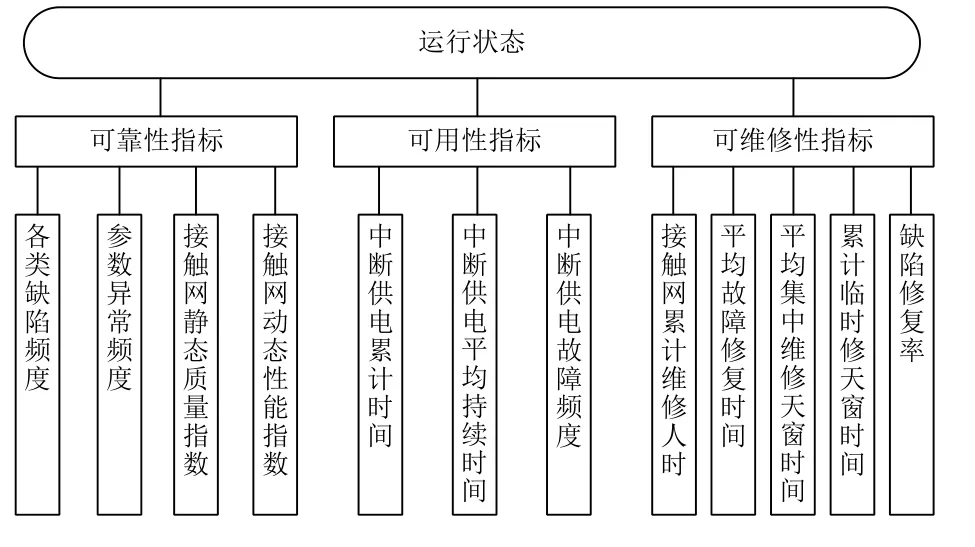
圖1 接觸網運行狀態評價體系

可靠性指標指在給定的條件下和給定的時間區間內，接觸網系統內各零部件及設備能完成要求的機械荷重、允許溫升、載流量、規定電氣作用等工作能力。主要考察接觸網幾何參數指標（如導高、拉出值）、平順性指標（如硬點）、弓網受流性能指標（如弓網接觸力、燃弧時間）以及接觸網零部件失效情況。其下屬二級指標包括各類缺陷頻度、參數異常頻度、接觸網靜態質量指數、接觸網動態性能指數。

可用性指標指接觸網系統在所要求的維修、管理等外部資源得到提供的情況下，在規定工況條件下，在給定的時間區間內可執行持續供電的能力。其下屬二級指標包括中斷供電累計時間、中斷供電平均持續時間和中斷供電故障頻度。

可維修性指標是指使用規定的程序和資源進行接觸網維修時，在給定的使用條件下，保持或恢復接觸網系統或零部件能完成要求的狀態的能力。其下屬二級指標包括接觸網累計維修人時、平均故障修復時間、平均集中修維修天窗時間、累計臨時修天窗時間和缺陷修復率。

1.2 接觸網運行狀態評價步驟

接觸網運行狀態的具體評價步驟如圖2 所示。

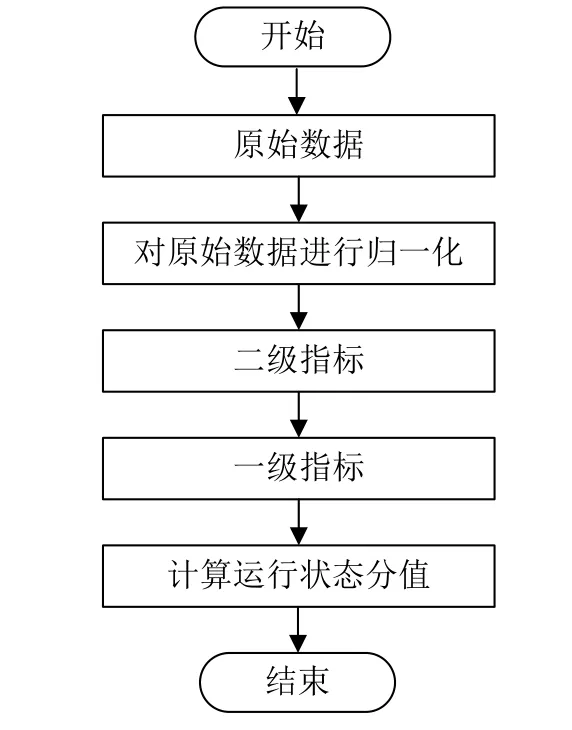
圖2 接觸網運行狀態評價步驟

采用min-max 歸一化法對各項原始數據進行同質化轉換，具體計算方法如式（1）所示。

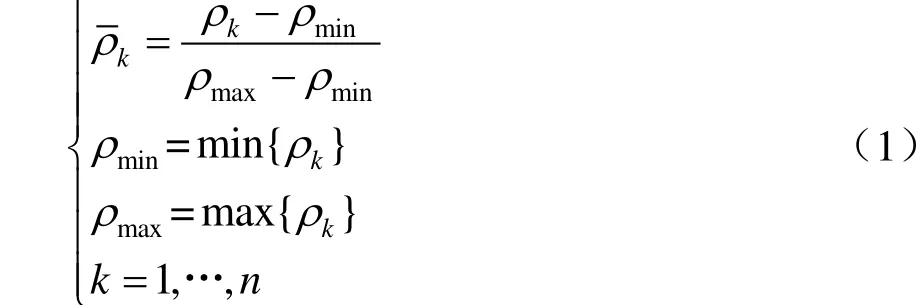
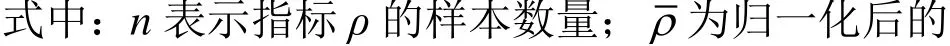
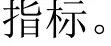
二級指標的權重由熵權法確定，即根據該指標的變異性的大小來分配權重[7]。一般來說，若某一指標的信息熵越小，表明該指標值變異程度越大，提供的信息量越多，在綜合評價中所能起到的作用也越大，反之亦然。設m為該二級指標ρk的取值個數，T為該一級指標下的二級指標總數。定義ρk的信息熵為

式中：ρfir為一級指標，W為權重值，ρsec為二級指標。

令ρre、ρse、ρma分別表示可靠性指數、可用性指數和可維修性指數，α、β、γ分別為對應的權重系數，且α+β+γ=1。一級指標的權重采用專家法確定，則接觸網系統的運行狀態由式（6）計算：

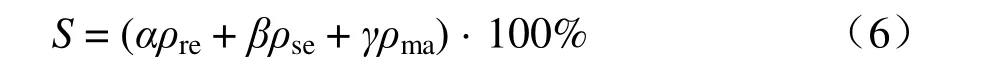
2 接觸網狀態退化過程

2.1 接觸網系統狀態退化模型

高速鐵路接觸網系統本身具有不對稱結構，使得接觸網系統受到頻繁的負荷沖擊，該類負荷具有典型的時間隨機性和空間隨機性，故相較一般電力系統，接觸網系統中設備的衰退更為快速和顯著。

Gamma 過程可以同時描述連續的微小沖擊導致的緩慢變化和劇烈沖擊引發的狀態突變，這正是接觸網運行狀態的典型退化特征[8]。故本文采用Gamma 隨機過程的方法對高速鐵路接觸網系統狀態在實行檢修維護等人工干預手段之前的退化過程進行建模，刻畫該過程中時空隨機性造成的影響。

設X(t)為接觸網系統狀態退化量，用于描述接觸網系統狀態在t時刻的衰退水平。則X(t)具有以下特征：（1）X(t)是一個單調遞增變量，即在兩次周期修作業期間，接觸網系統退化量會隨時間逐漸增加；（2）假設接觸網系統周期修后狀態與初始狀態一致，則有X(0) = 0；（3）接觸網系統在給定時間間隔Δt內，ΔX服從參數為a和b的Gamma 分布，即具有如下形式的概率密度函數：

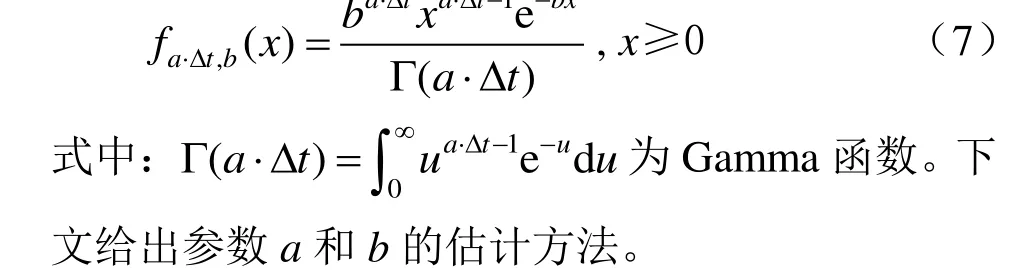
2.2 接觸網系統狀態退化模型參數估計

Gamma 函數的參數a和b被稱為形狀參數與尺度參數，具有明確的統計意義，即Gamma 過程的平均退化量（期望）為a/b，偏離平均退化量的不確定程度（方差）為1/b2。

在一個維修周期內每間隔兩天計算一次接觸網系統狀態分值，得到接觸網系統狀態分值序列Sn。則接觸網系統退化量序列計算式為

求解式（9），可得接觸網系統狀態退化過程參數。

3 接觸網維修計劃調整方案

3.1 主動維修策略

接觸網系統主動維修決策過程是保持接觸網系統具備良好運行狀態的同時，將系統維護成本控制在較低的水平，進而達到系統運行狀態和經濟性的最佳平衡。假設連續兩次周期修期間接觸網系統的退化模式未發生顯著改變，即相鄰兩次接觸網維修周期的退化參數具有一致性。通過上一維修周期內接觸網狀態變化特征，預測本周期內接觸網運行狀態發展趨勢，制定合理的臨時修計劃。

從系統安全性角度出發，高速鐵路接觸網系統大部分故障隱患是隱性的，出于成本和可靠性等方面的考慮，目前實際投入接觸網系統運維的在線檢測設備數量是有限的[2]，不利于發現接觸網系統早期故障。但從接觸網系統退化模型出發（圖3），當退化量曲線X(t)出現峰值，表征接觸網系統發生影響其運行狀態的故障隱患，判定條件為

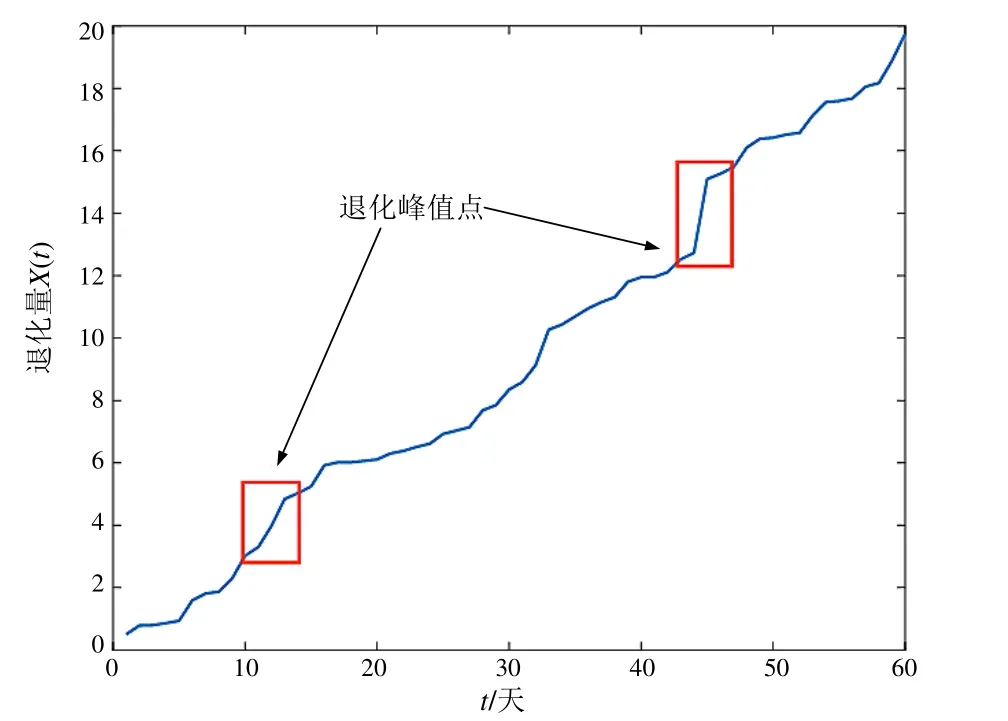
圖3 接觸網運行狀態退化曲線

式中：η表示退化閾值，根據線路狀況確定。

根據接觸網系統運行狀態評價模型，逆向查找引發運行狀態得分下降的因素，并安排針對性的巡視檢修計劃。

另一方面，接觸網系統維修策略的制定原則是在保障接觸網系統安全可用的同時降低維護成本。為了對維修策略的性能進行定量評價，提出評價指標—性能退化成本率CR，其定義式為

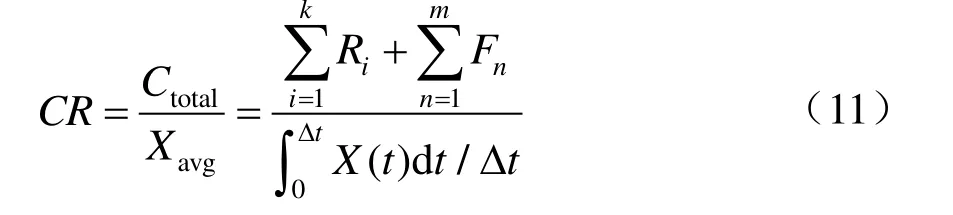
式中：Xavg為單個維修周期內接觸網系統平均退化量，Ctotal為維修周期內合計維修成本，Ri為第i次臨時修成本，Fn為第n次故障引發的損失。

性能退化成本率CR的物理意義是衡量鐵路運營部門抵消接觸網系統性能退化的影響所付出的成本。由于退化量和成本計算的復雜性，可采用蒙特卡洛方法求得接觸網狀態突變判定閾值與最優維修計劃[9]。

3.2 計劃修周期調整

高速鐵路接觸網系統的動態性能特征與整體性能的退化趨勢具有一致性[10]。常用的傅里葉變換雖然能夠準確提取信號的頻譜，但無法將信號的頻率與時間關聯。當接觸網動態檢測參數出現異常時，往往需要分析其發生突變的時間，時頻關系的確定則尤為重要。對接觸網動態幾何參數的時頻特征進行分析，為掌握接觸網運行狀態提供了有效參考。

將接觸網幾何參數動態檢測視為一個非平穩信號，采用Hilbert-Huang 變換可以提取其時頻信息。具體步驟如下：

（1）采用經驗模態分解（EMD）對該信號進行平穩化處理，自適應地將接觸網幾何參數動態檢測信號Y(t)分解為多個窄帶寬的內涵模態分量（IMF）[11]：

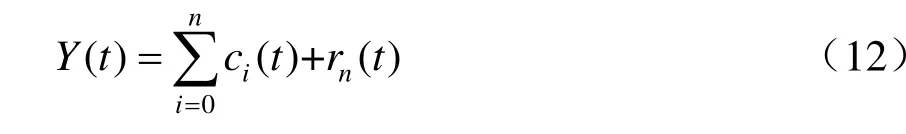
式中：ci(t)表示第i階內涵模態分量；rn(t)表示殘余分量。

（2）將EMD 分解得到的IMF分量進行Hilbert變換得到信號的瞬時頻率及能量，對IMF 各個分量進行Hilbert 變換：

以時間為橫坐標、頻率為縱坐標建立平面坐標系，將幅度表示為瞬時頻率和時間的函數，繪制的圖譜即Hilbert 譜：

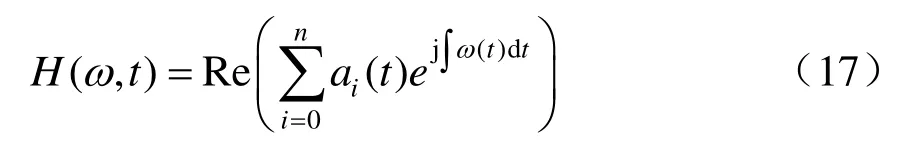
對單趟接觸網動態檢測數據的Hilbert 譜求和，可以得到當前接觸網動態幾何參數的能量和。當線路狀態良好時，動態幾何參數較為平順，能量和小；線路狀態退化時，動態幾何參數波動劇烈，高頻分量幅值增大，能量和較大。

如圖4 所示，當能量和一旦超出臨界值時，能量和呈陡增狀態，經過維修處理后，接觸網性能得到改善，能量和明顯下降。

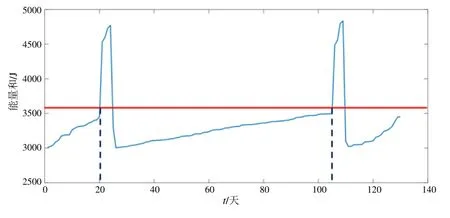
圖4 接觸網動態檢測參數能量和趨勢

對于某線路的檢測數據，通過關聯其歷史數據，找到能量和變化臨界值及變化周期，將計劃修周期制定為兩次超限值發生日期的時間間隔。

4 線路驗證分析

4.1 接觸網系統狀態評價體系指標權重的計算

選取我國東部某高速鐵路動車段7 區間8個站點在2021 年7 月—2021 年9 月的檢修數據、動靜態檢測數據、缺陷記錄、故障記錄，驗證本文提出的接觸網系統狀態體系的有效性。

根據專家法可得各一級指標權重向量為[α,β,γ]= [0.4,0.5,0.1]，計算各個一級指標下二級指標的熵值，得到各個二級指標權重如表1 所示。

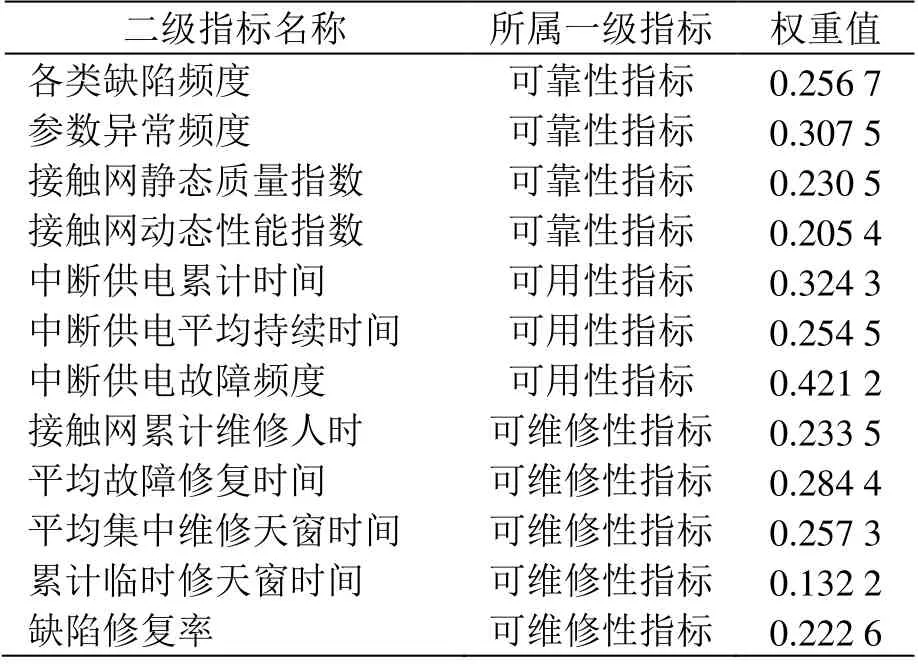
表1 二級指標權重

4.2 確定接觸網系統狀態退化過程特征

計算2021 年第3 季度該線路接觸網運行狀態的趨勢，每間隔2 天計算1次線路運行狀態值序列，得到Sn= {99.9，99.4，95.7，94.9，94.0，93.3，91.2，88.8，87.0，86.8，85.0，84.6，84.6，83.7，81.9，81.6，81.5，81.0，80.5，79.8，79.4，78.6，78.4，77.5，77.2，76.8，75.6，72.5，71.4}。

繪制接觸網系統狀態值曲線如圖5 所示。可以看出，接觸網運行狀態分值在單一維修周期內呈單調下降趨勢，符合Gamma 過程的基本假設。

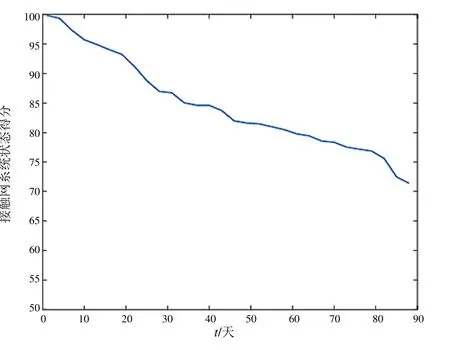
圖5 接觸網系統運行狀態分值曲線

根據式（8）計算接觸網系統退化值序列Xn，得到Xn={0.1，0.6，2.6，4.3，5.1，6.0，6.7，8.8，11.2，13.0，13.2，15.0，15.4，15.4，16.3，18.1，18.4，18.5，19.0，19.5，20.2，20.6，21.4，21.6，22.5，22.8，23.2，24.4，27.5，28.6}。進而求得退化序列的均值為15.33，方差為63.11，代入式（9）可求得接觸網退化模型參數：a=121.78，b=7.94。

4.3 接觸網系統主動維修計劃建議

根據序列Xn計算線路接觸網系統運行狀態退化量的差分量并繪制其累計分布函數（CDF）如圖6 所示。

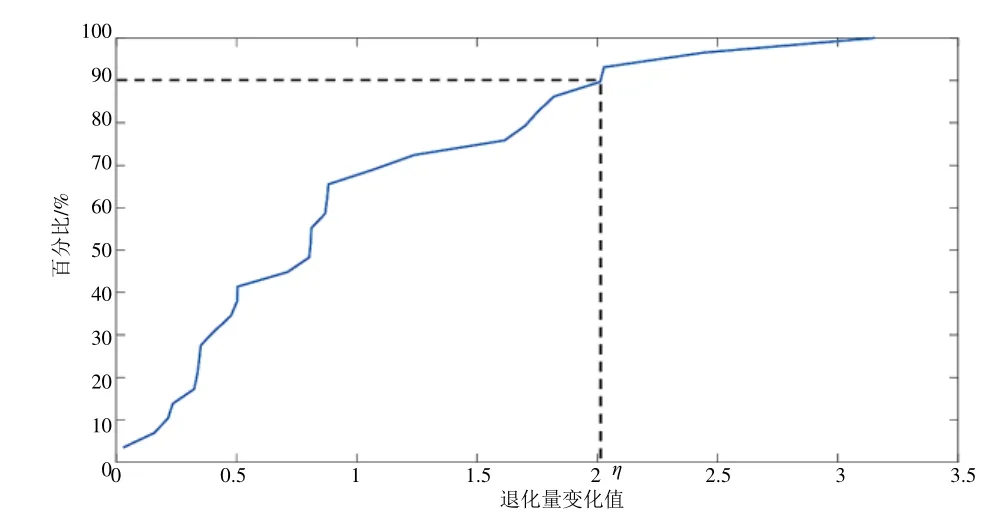
圖6 接觸網系統運行狀態退化量變化值的累積分布函數

認為接觸網系統在90%的時間處于低風險狀態，10%概率出現故障隱患，即式（10）中觸發臨時修的閾值η對應為CDF 曲線值為0.9 時的退化量變化值，故η=2.02。

采用蒙特卡洛算法計算得到單次維修派遣人數和維修工時，如表2 所示。

表2 單次維修詳情

該季度內臨時修共計85 人·時，較2020 年3季度—2021 年2 季度的平均值(103 人·時)下降17.48%。且該季度內僅因雷擊造成跳閘故障2 次，較2020 年3 季度—2021 年2 季度的平均值（3.7次）下降45.95%，大幅減少因線路故障引發的經濟損失，按式（11）計算綜合成本下降24%。由此，可證實所提主動維修策略的有效性，既能保證線路處于低故障風險，又可實現最低維修成本。

4.4 線路計劃修周期建議

選取接觸線高度為目標幾何參量，每隔兩天對線路動態接觸線高度檢測結果進行抽樣，選取5 條動態檢測數據文件分別進行HHT 分解，計算其能量和的均值作為當日線路能量和。2021 年第3 季度內線路動態接觸線高度能量和趨勢見圖7。

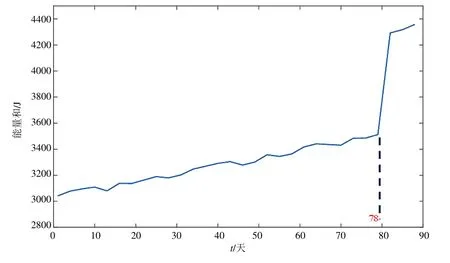
圖7 動態接觸線高度能量和趨勢

從圖中可以得出以下結論：

（1）動態接觸線高度能量和在一個維修周期內總體呈上升趨勢，但受到檢測設備誤差與外部環境因素的影響，導致部分時間點接觸線高度能量和出現振蕩。

（2）本季度第78 天能量和為3 512 J，此后能量和劇增，可以推斷動態接觸線高度能量和臨界值約3 500 J，建議調整計劃修周期縮短至80 天。

（3）第81 天能量和劇增時，接觸網系統運行狀態出現退化峰值點，映證兩者對接觸網系統運行狀態的刻畫具有一致性。

5 結語

本文綜合考量影響接觸網運行狀態的因素，建立高速鐵路接觸網系統運行狀態評價體系，推導基于Gamma 過程的接觸網系統狀態退化模型。在此基礎上結合HHT 時頻分析方法提出主動維修建議和最佳接觸網維修周期。結合某高鐵實際運營數據表明：接觸網狀態評價體系與退化模型可準確全面地描述接觸網狀態發展趨勢；主動維修策略和維修周期建議在消除接觸網系統故障隱患的同時能更合理地統籌維修資源，綜合維修成本下降約24%。綜上，本文所述方案切合接觸網系統運營需求，具有一定的實際應用價值。