三軸壓縮條件下單裂隙巖樣裂隙擴展研究

陳祥， 肖桃李， 折海成

(長江大學城市建設學院， 荊州 434023)

頁巖儲層脆性大，天然裂縫和水平層理發育，壓裂過程中容易發生剪切滑移和張性破壞[1]，導致在頁巖氣儲層鉆井過程中，井壁坍塌失穩等事故頻發。大量工程實踐表明，裂隙巖石的失穩破壞，通常是受到巖石內部裂隙萌生、擴展、貫通的影響。同時，圍壓與巖石內部裂隙的長度對巖石內部裂紋的萌生與擴展起著不可或缺的作用。因此，研究巖石中裂隙起裂、擴展、貫通和破壞等缺陷擴展演化特性，對分析油氣開采過程中巖體內部裂紋的擴展具有重大意義。

Shen等[2]和Wong等[3]對類巖樣材料進行單軸試驗分析不同裂隙深度、裂隙傾角及材料性質對預制裂隙巖樣的貫通機制。張志婷等[4]對含不同巖橋長度的花崗巖試件進行三軸加載試驗，采用紅外熱成像與聲發射技術對巖石試件破壞前兆進行分析。莊賢鵬等[5]對含預制裂隙砂巖巖樣進行單軸循環加卸載試驗，發現在加卸載作用下，砂巖巖樣峰值強度與彈性模量呈現出顯著的強化現象。李術才等[6-7]和李延春等[8]對預制單裂隙類巖樣材料進行三軸試驗，同時均采用CT掃描技術進行研究，分析單裂隙巖樣的微觀損傷機理以及巖樣內部裂隙的發育過程與擴展機制。文獻[9-11]對錦屏深部大理巖進行單軸加、卸載以及三軸壓縮和高應力條件下的峰前、峰后卸圍壓等4種不同應力路徑力學試驗；以及得到錦屏大理巖在加、卸載應力路徑下存在力學特性差異的結論。劉曉燕等[12]對錦屏二級水電站深部大理巖的三軸壓縮試驗研究表明: 錦屏深部大理巖在低圍壓下，沒有明顯的擴容現象，隨著圍壓的增加，巖體的峰值強度、殘余強度增加，巖體由脆性向延塑性轉化。肖桃李等[13-14]對大理巖及類巖樣材料進行室內三軸試驗，提出了普遍存在的三種裂紋即I型裂紋(拉伸裂紋)、Ⅱ型裂紋(滑移型裂紋)、Ⅲ型裂紋(撕開型裂紋)，同時發現巖樣在低圍壓時，以剪切-拉伸復合破壞為主；中圍壓時，為宏觀的X型剪切破壞；高圍壓時，則表現為沿預制裂隙面的剪切破壞模式。Nasseri等[15]、Niandou等[16]開展頁巖的三軸壓縮試驗，分析了頁巖傾角、圍壓與強度的關系，進一步探討裂隙傾角和圍壓對各力學參數的影響，發現巖樣有3種不同的破壞形式，同時發現頁巖層理面傾角和圍壓是影響試件按不同形式破壞的主要因素。文獻[17-20]通過對類巖石材料進行室內三軸試驗并結合顆粒流數值模擬，發現試驗中巖樣各力學參數隨圍壓的增大而增大；低圍壓時表現為單一斜剪破壞，中等圍壓時表現為類似X型(翼裂紋從原生裂隙兩端起裂)的剪切破壞，高圍壓時則表現出沿結構面的滑動剪切破壞的結論。鄭晨等[21]通過有限元軟件模擬分析了隧道開挖過程中裂隙巖體的變形破壞特點以及并討論了Barton-Bandis準則中節理粗糙程度 的取值對圍巖穩定性的影響。還有些學者[22-23]通過有限元法或離散元法對巖樣三軸試驗進行模擬，發現隨著裂隙長度的增加，巖樣的強度和變形參數均呈降低趨勢同時發現圍壓對巖石峰值強度有強化作用，但圍壓卻無法改變巖石的峰值強度隨裂隙傾角增大而減小的變化規律。

從諸多學者的研究中不難發現，在室內單軸、三軸試驗基礎上結合數值模擬，對研究巖樣力學特性與裂紋擴展規律提供更加準確的依據。但從微細觀角度對巖樣內部裂紋的萌生、發育、擴展及貫通規律的研究較少。因此，現基于錦屏深部大理巖的室內試驗參數，人工制備含不同裂隙長度的類巖石巖樣，在不同圍壓條件下進行三軸試驗，同時采用PFC2D數值模擬軟件從巖樣的宏觀與微細觀角度對巖樣各力學參數、破壞模式、裂紋擴展與微裂紋數量進行分析。

1 單裂隙大理巖常規三軸試驗

1.1 試驗設置

在油氣開采過程中，壓裂的巖體內部存在著大量的孔隙、節理與空洞等。試驗時為了減小誤差，會對部分巖石進行篩選，然而現場取樣難以找到相似的巖樣進行實驗。本文根據錦屏大理巖巖樣參數，通過室內人工制備巖樣來獲取大量相似的試驗巖樣，采用室內制備的相似巖樣進行試驗。試驗特制的高強硅粉砂漿材料的配比為425#普通硅酸鹽水泥∶微硅粉∶石英砂∶鐵粉∶高效減水劑∶水=1∶0.13∶0.8∶0.25∶0.02∶0.325(質量比)。為了提高模型巖樣與巖石原樣的一致性，同時提高混凝土巖樣的致密性及減小材料的孔隙率，通過在模型材料的配合比設計中添加鐵粉增加巖樣密度，添加超細硅粉降低巖樣孔隙率。巖樣標準尺寸為φ50 mm×100 mm，制備出的模型巖樣如圖1所示。為研究裂隙長度及圍壓對巖樣力學特性及裂紋擴展規律的影響，因此設計不同的裂隙長度與圍壓進行實驗，各工況試驗方案如表1所示。

1.2 PFC2D模型的建立

在顆粒流數值模擬軟件(particle flow code，PFC)建模中，通過PFC2D中內置的Fish語言按照巖樣尺寸為50 mm×100 mm生成模型，然后自動生成球體填充，通過刪除預制裂隙位置的顆粒形成預制裂隙，使用頂部和底部墻壁的相對運動速率模擬應變控制，給側墻賦予剛度模擬圍壓進行三軸壓縮試驗。圖2中A模型裂隙長度為13 mm，裂隙傾角為60°。

L為預制裂隙長度；α為預制裂隙傾角圖1 單裂隙巖樣裂隙分布與模型巖樣圖Fig.1 Single crack sample distribution and model sample figure

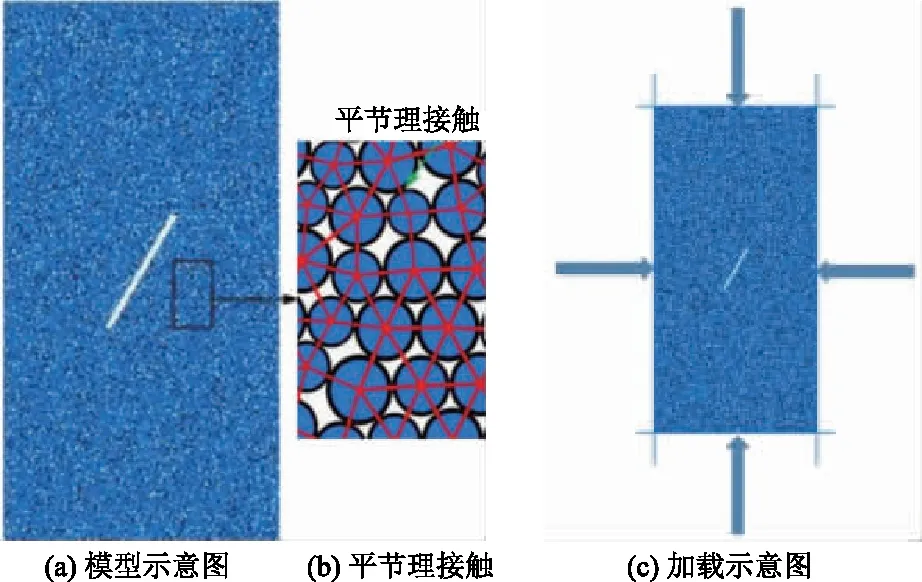
圖2 A模型及模型加載示意圖Fig.2 A model and model loading diagram

通過室內試驗獲取的巖樣參數，基于陳鵬宇等[24]的研究，采取調整之后的試錯法，調節模型細觀參數，使通過數值模擬得到的應力-應變曲線與試驗曲線基本吻合。通過施加0.04 m/s的軸向荷載來模擬單軸壓縮試驗。模型中，模型巖樣顆粒數共計26 308個，顆粒間相互接觸點有50 716個。此時所確定的模型巖樣的物理力學參數，如表2所示，數值模擬與試驗所得到的完整樣應力應變曲線如圖3所示。

表2 數值模擬參數設置Table 2 Numerical simulation parameter setting

由圖3可知，在壓縮過程中，室內試驗的應力-應變曲線中有一段向下凹的壓密過程，與數值模擬的應力-應變曲線壓密階段存在差異。這是因為在數值模擬中，采用的是刪除顆粒法，所得到的模型中顆粒之間的接觸都已經相對密實了，但室內試驗中的巖樣都存在一些空隙與微裂紋。數值模擬所得到的單軸抗壓強度為70.12 MPa，室內試驗得到的單軸抗壓強度為70.65 MPa，偏差在0.75%；數值模擬與室內試驗得到的彈性模量均為14.19 GPa，說明通過PFC得到的力學參數與室內試驗得到的相近。圖3中給出了數值模擬與室內試驗的巖樣最終破壞模式圖，兩者均表現為剪切破壞，所得破壞模式較為匹配，因此采用PFC數值模擬與室內試驗所得的力學參數與破壞模式是相符的，可以采用PFC代表室內試驗。

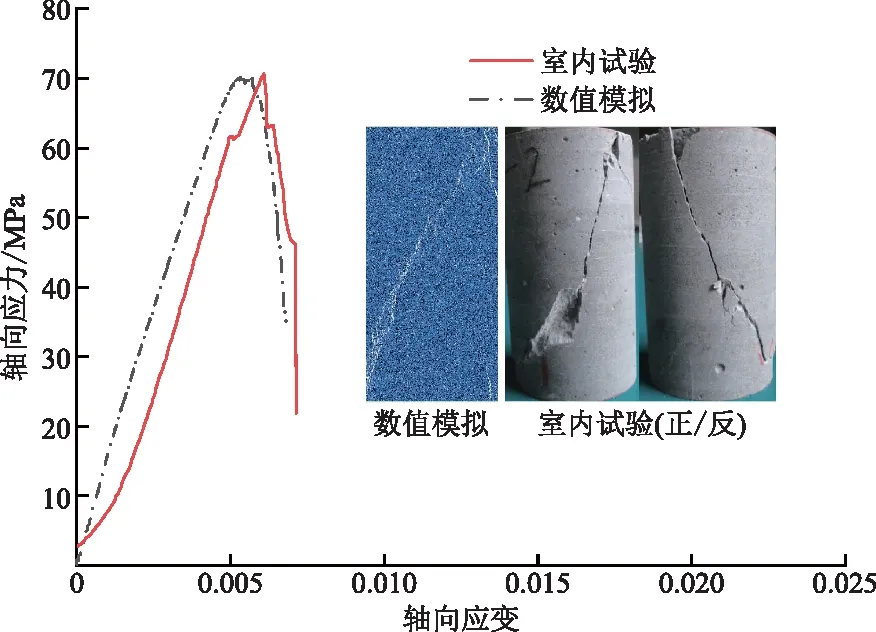
圖3 三軸壓縮條件下室內試驗與數值模擬應力應變曲線Fig.3 Laboratory test and numerical simulation of stress-strain curves under triaxial compression

2 單裂隙巖樣與數值模擬破壞模式及力學特性分析

2.1 單裂隙巖樣與數值模擬破壞模式分析

將室內三軸壓縮試驗和PFC數值模擬得到的巖樣破壞模式進行對比分析，如圖4～圖6所示。破壞模式圖是以不同顏色線條來區分不同方式的擴展裂紋，用深藍色粗線代表預制裂隙所在部位、用紅色線條編號①代表共面裂紋，于預制裂紋尖端開始發育，在三軸試驗中與預制裂紋面走向大體一致，是預制裂隙自相似擴展的產物；用藍色線條②代表反翼裂紋，它既可能萌生于預制裂紋尖端或中部，也可能從新裂紋某處開始，在三軸試驗中與預制裂紋面走向相反；用綠色線條③代表數值模擬實驗中預制裂隙位置；用紫色裂紋④代表支裂紋，它的起裂點可能位于預制裂紋中部，也可能至預制裂紋中部一段距離開始的支裂紋。

由圖4可知，當L=13 mm、α=60°時，裂紋沿著預制裂隙的角度進行發展，一直延伸到端部發生剪切破壞。當裂隙長度一定時，隨著圍壓的增加，巖樣的破壞程度越大，且巖樣均以單一剪切破壞為主，與模擬結果較為吻合。

圖4 A巖樣軸壓縮試驗和數值模擬的破壞模式對比圖Fig.4 Comparison of failure modes between axial compression test and numerical simulation of rock sample A

由圖5可知，當L=39 mm、α=60°時，裂紋沿著預制裂隙方向發展并在預制裂隙下端部產生翼裂紋，并同時向巖樣端部延伸，到達端部發生破壞且大部分以Y型破壞為主。隨著圍壓的增加，拉伸裂紋與翼裂紋夾角逐漸增加且巖樣破壞程度也隨著增大。

圖5 B巖樣軸壓縮試驗和數值模擬的破壞模式對比圖Fig.5 Comparison of failure modes between axial compression test and numerical simulation of rock sample B

圖6 C巖樣軸壓縮試驗和數值模擬的破壞模式對比圖Fig.6 Comparison of failure modes between axial compression test and numerical simulation of rock sample C

由圖6可知，當α=90°、σ3=14 MPa時，L由13 mm增大到26 mm最后增大到39 mm，裂紋擴展規模逐漸增大，巖樣大部分以X型破壞為主。

由圖4～圖6可知，通過PFC2D模擬出的巖樣破壞模式與室內三軸壓縮試驗所得到的破壞模式十分接近，因此可以使用PFC2D模擬出的巖樣破壞過程代表室內試驗的破壞過程。由于只能從室內三軸壓縮試驗所得的巖樣破壞圖中獲取到宏觀裂紋的分布和擴展痕跡，無法從微細觀角度來分析巖樣在實驗過程中的起裂、擴展及破壞規律，因此十分有必要采用PFC數值模擬來做進一步研究分析，進而揭示含單裂隙巖石在三軸壓縮作用下裂紋萌生、起裂、擴展、貫通直至破壞整個過程的機理。

2.2 單裂隙巖樣與數值模擬力學特性分析

通過數值模擬所得應力應變曲線可得到不同圍壓，不同裂隙長度下的峰值強度、彈性模量等力學參數，各參數對比圖如圖7和圖8所示。

圖7 不同圍壓、不同裂隙長度下的峰值強度Fig.7 Peak strength under different confining pressures and different crack lengths

由圖7可知，當α=60°，當圍壓一定時，隨著裂隙長度的增加，巖樣的峰值強度逐漸減少，且各圍壓條件下，峰值強度隨裂隙長度增大而下降的趨勢不受影響。當裂隙長度一定時，巖樣的峰值強度隨圍壓呈線性增長，這表明圍壓條件下裂隙對巖體的峰值強度影響更為明顯。這主要是因為圍壓的存在使巖樣內部微孔隙閉合，在巖樣發生破壞時限制了側向位移，提高巖樣的抗壓強度，從而使得巖樣在裂隙尺寸相同的條件下，圍壓越大，峰值強度越大，且圍壓對巖樣峰值強度的影響獨立于裂隙尺寸對巖樣峰值強度的影響。

由圖8可知，當σ3=14 MPa時，峰值強度隨裂隙長度增加呈現先增大后減小的倒V形趨勢，在L=26 mm處取最大值，說明當圍壓一定時，巖樣在某一長度峰值強度取最大值且與裂隙長度的變化無關。相比圍壓的影響而言，峰值強度受裂隙長度的影響幾乎可以忽略不計。

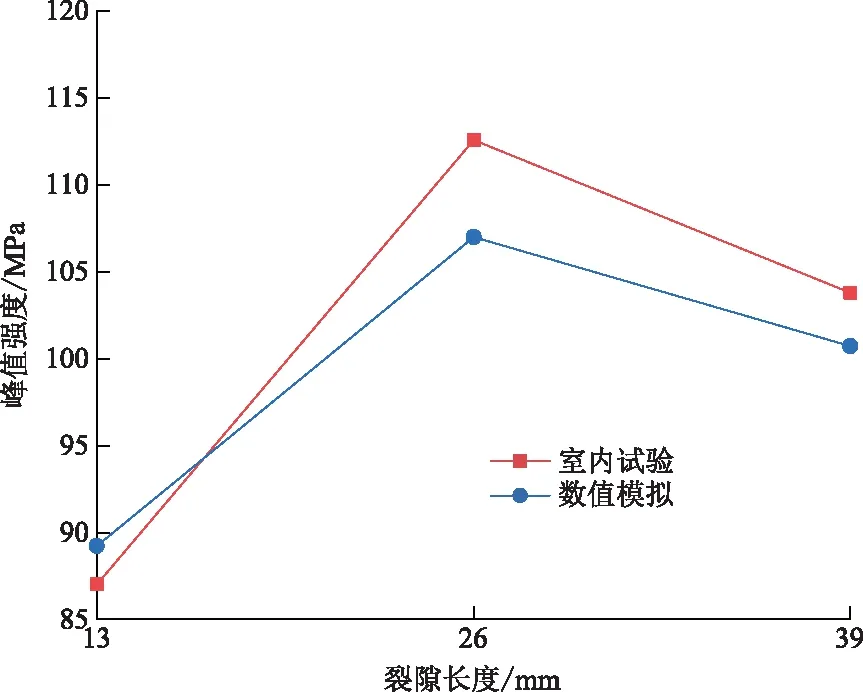
圖8 圍壓為14 MPa時，不同裂隙長度下的峰值強度Fig.8 Peak strength under different crack lengths at 14 MPa confining pressure

在巖石變形破壞過程中，裂紋經歷了壓密、起裂、擴展、貫通4個擴展階段[25]，每個階段劃分都對應著特定的應力閾值，即與裂紋起裂、擴展和貫通相關的特征應力有起裂壓力、損傷壓力和峰值應力。三軸壓縮試驗中，巖樣裂紋的擴展受到巖石力學性質、裂隙長度和圍壓等因素的影響，同時這些因素也會決定著裂紋的起裂應力與損傷應力的大小。

本文選擇α=60°分析裂隙長度與圍壓對起裂應力(σci)與損傷應力(σcd)的影響。根據劉泉聲等[26]基于Griffith理論修正之后的起裂應力預測經驗計算方法，同時采用側向應變差法 (LSR)[27]將模擬過程中測得的軸向應力-軸向應變曲線、軸向應力-側向應變曲線和軸向應力-體積應變曲線進行處理，得到三軸壓縮條件下含單裂隙巖樣的起裂應力與損傷應力大小，如圖9所示。

由圖9可知，裂隙長度一定時，起裂應力與損傷應力均隨圍壓增大而增大，說明隨著圍壓的增大，巖樣的強度特性逐漸提高。同時當圍壓一定時，起裂應力與損傷應力隨著裂隙長度增大逐漸減小，說明隨裂隙長度增大，減小了含裂隙段巖樣橫截面積的有效面積，裂隙長度越長，起裂應力與損傷應力越小，更為容易的萌生新生裂紋以及發生破壞，巖樣強度特性降低。

圖9 不同圍壓條件下起裂應力與損傷應力變化規律圖Fig.9 Diagram of crack initiation stress and damage stress variation under different confining pressures

由圖10可知，當裂隙長度一定時，隨著圍壓增加，巖樣彈性模量呈上升趨勢。這是因為圍壓越大，巖石微裂紋閉合程度越大，致密性增加，彈性模量越大。當圍壓一定時，裂隙長度增大，減小了含裂隙段巖樣橫截面積的有效面積，裂隙長度越長，起裂應力與損傷應力越小，更為容易的萌生新生裂紋以及發生破壞，巖樣強度特性降低。

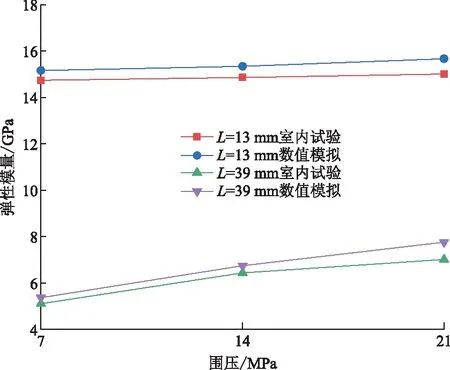
圖10 不同圍壓、不同裂隙長度下的彈性模量Fig.10 Elastic modulus under different confining pressure and different crack length

3 含單裂隙巖石裂紋起裂與擴展規律

由巖石斷裂力學中的微裂紋成核理論可知，巖石的破壞并非一下從原始狀態就突然發生的，其要經歷微裂紋的萌生、發育、集結(成核)等一系列演化過程。巖石微裂紋成核理論認為，在微裂紋萌生初期，由于密度不高，其相互作用可以忽略，每個微裂紋的行為可以當成孤立的，但當微裂紋的密度達到一定閾值的時候，其相互作用不可忽略。在離散元軟件中，對顆粒與顆粒之間進行研究，顆粒與顆粒之間的平行黏結破壞機理如圖11所示。

圖11 PFC2D中平行黏結破壞機理Fig.11 Failure mechanism of parallel bonding in PFC2D

采用PFC顆粒流軟件進行模擬并分析巖樣加載過程中的總裂紋數量、剪切裂紋數量和張拉裂紋數量3個因變量與軸向應變之間關系，從微細觀角度研究巖樣微裂紋的萌生與擴展。

由圖12和表3可知，剪切裂紋在整個模擬加載過程中占主導地位且數量始終占比較大。隨著圍壓的增加，L=13 mm時，拉裂紋占比從12.58%增長到23.06%，圖中剪切裂紋曲線逐漸變得較為平緩，拉伸裂紋曲線逐漸變陡。

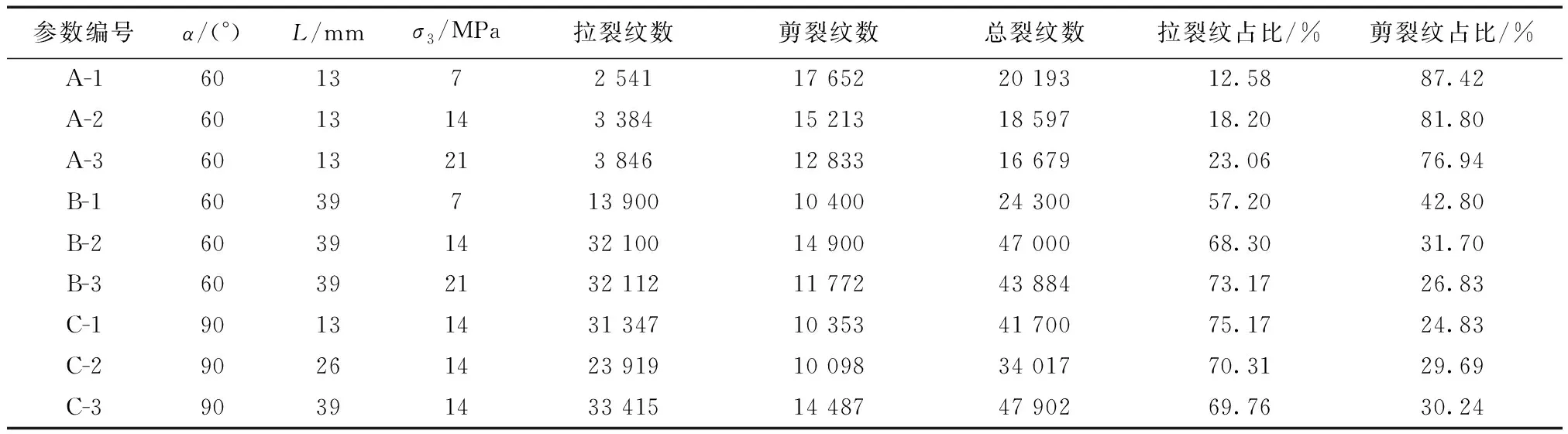
表3 數值模擬所得巖樣裂紋數量表Table 3 Number of cracks in rock samples obtained by numerical simulation

由圖13和表3可知，L=39 mm時，拉裂紋占比從57.202%增長到73.175%，圖中軸向應變較小時，剪切裂紋占比大于張拉裂紋，隨著軸向應變的增加，拉裂紋逐步發育超過剪裂紋，并在之后的加載過程中占據主導地位，且隨著圍壓的增加拉伸裂紋曲線有明顯的大幅度增加，21 MPa時拉裂紋數量為剪裂紋數量的2.73倍。

由圖14和表3可知，當圍壓一定時，隨著裂隙長度的增加，拉裂紋占比從75.173%逐步減少到69.757%，圖中拉裂紋曲線也逐步變平緩。

由圖12～圖14與表3可知，巖樣加載初期裂紋較少，巖樣處于彈性階段；隨著軸向應變的增加，裂紋數量逐漸增多，巖樣進入塑性階段；當軸向應變超過峰值應變時，裂紋急速生長并產生貫通，巖樣發生破壞；進入殘余階段之后裂紋的數量基本保持不變。

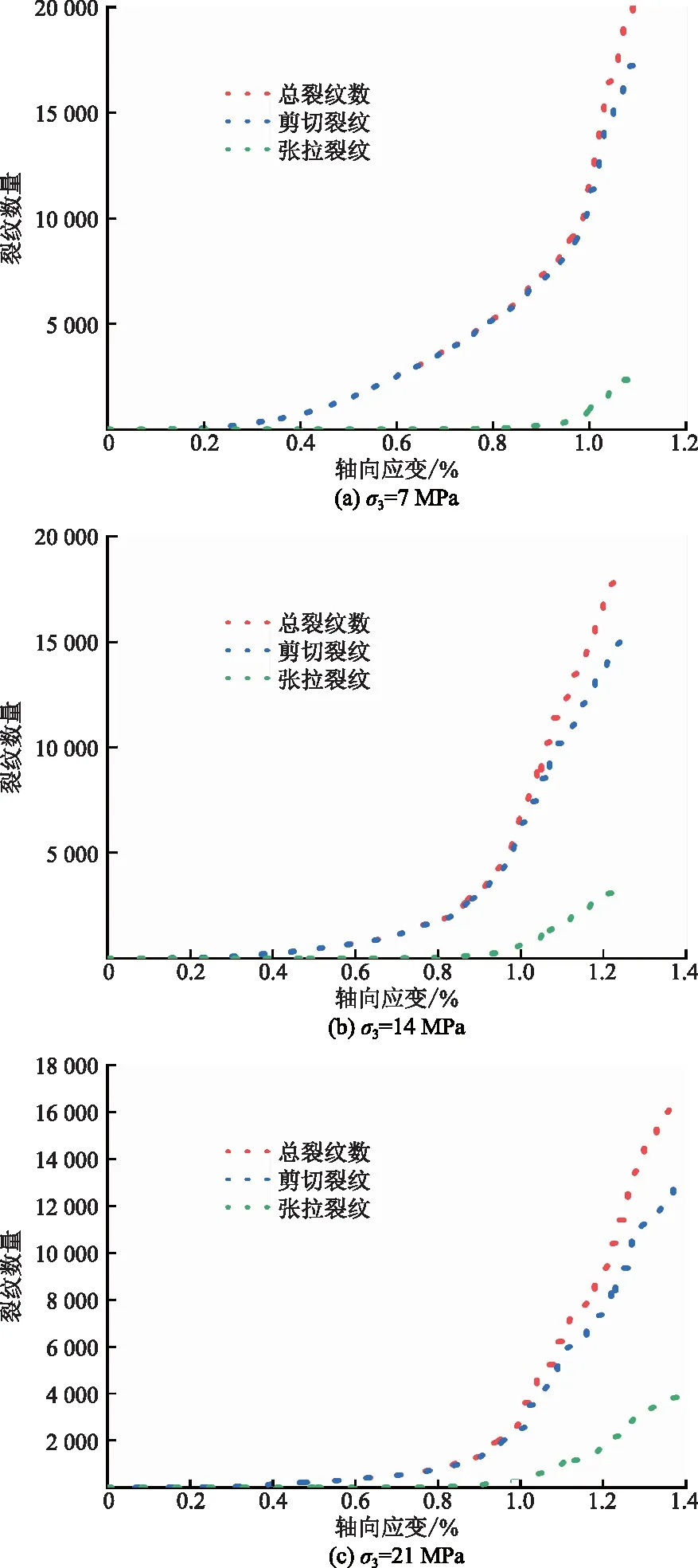
圖12 A巖樣數值模擬過程中裂紋數量變化圖Fig.12 Variation of crack number in rock sample A during numerical simulation

圖14 C巖樣數值模擬過程中裂紋數量變化圖Fig.14 Variation of crack number in rock sample C during numerical simulation

圍壓較小時，剪裂紋在巖樣加載整個過程中占據主導地位，隨著軸向應變的逐漸增加，拉裂紋迅速生長，但剪切裂紋仍舊高于張拉裂紋。隨著圍壓的增加，張拉裂紋數量急劇增加，隨著軸向應變的增大逐步超越剪切裂紋并占據主導地位，這是因為顆粒間平行黏結的抗剪強度符合莫爾庫倫準則(圖11)， 隨著圍壓升高，平行黏結的抗剪強度增加、抗拉強度不變，因此顆粒間發生剪切破壞的難度也逐漸變大。

為了進一步研究裂隙長度與圍壓對裂紋擴展的影響，選擇A與C系列模型巖樣進行分析，對其數值模擬所得裂紋進行標記與研究。其中黑色裂紋代表預制裂隙，紅色代表剪切裂紋，黃色代表拉伸裂紋，得到圖15與圖16。

由圖15與圖16可知，隨著圍壓的增加，拉裂紋逐步出現且占比逐步增大。且破裂帶隨著圍壓的增加而增大，巖樣隨著圍壓的增加破壞程度逐漸增大。隨著裂隙長度的增加，拉裂紋破裂帶逐步減少，總破裂帶反而逐漸增加。隨著圍壓的增加，拉裂紋逐步增加；破裂帶范圍也增大，但裂隙長度對破裂帶的發育影響更為迅速。

圖15 A系列式樣不同圍壓條件下數值模擬裂紋破裂帶分布示意圖Fig.15 A series patterns under different surrounding pressure conditions numerical simulation crack crack band distribution schematic

圖16 C系列式樣不同裂隙長度數值模擬裂紋破裂帶分布示意圖Fig.16 The C-Series pattern numerically simulates the distribution of crack crack bands for different crack lengths

4 結論

通過對含單裂隙巖樣進行三軸壓縮試驗，并采用PFC2D軟件對微裂紋數量與剪切帶進行分析，得到以下結論。

(1)當圍壓為7 MPa時，巖樣以剪切-拉伸復合破壞模式為主；當圍壓為14 MPa時，巖樣以Y型剪切破壞、單一斜剪破壞模式為主；當圍壓為21 MPa時，巖樣以X型剪切破壞模式為主。圍壓是巖樣宏觀破壞模式的主要影響因素，預制裂隙的長度主要影響裂紋的擴展規模，即翼裂紋與反翼裂紋、拉伸裂紋的發育軌跡。

(2)隨著圍壓的增大，巖樣的峰值強度、起裂應力、損傷應力與彈性模量均呈增長趨勢；隨著裂隙長度的增加，各力學參數均逐漸下降。

(3)隨著圍壓的增加，拉裂紋占比逐步增加，剪切裂紋占比減少；當裂隙長度為39 mm，圍壓為21 MPa時拉裂紋數量為剪裂紋數量的2.73倍。圍壓與裂隙長度增加，破裂帶均增大，但裂隙長度對破裂帶的發育影響更為迅速。