基于在線參數辨識的變體飛行器控制

王子健,張書宇,侯明哲

(哈爾濱工業大學， 哈爾濱 150001)

1 引言

大多數飛行器具有固定的氣動外形，這種固定氣動外形的飛行器往往只能適應單一或少數幾種飛行任務，但是變體飛行器能夠在不同的飛行環境下，通過改變自身的外形從而提升飛行性能以滿足不同的飛行任務需求，所以變體飛行器的控制問題是當前航空航天領域的熱點問題之一。常見的變形方式可以按照變形尺寸概括為三類：小尺寸變形，如局部鼓包等方式改變飛行器的氣動性能；中尺寸變形，如改變機翼的厚度等；大尺寸變形，如改變機翼翼展、后掠角等方式。其中大尺寸變形對飛行器的氣動性能影響最大，所以相關研究也大多集中在這一領域。

目前大部分研究都集中于變體飛行器的變形-飛行協調控制問題，即飛行器變形過程中的穩定飛行控制或跟蹤控制問題。文獻[4]提出了一種抗飽和平滑切換控制策略，以解決飛行器變形過程中的姿態穩定控制問題。文獻[5]針對可變后掠角飛行器建立了切換模型，研究了飛行器外形變化下的跟蹤控制問題。文獻[6-7]針對可變翼展與后掠角的變體飛行器建立了線性變形參數模型，設計了魯棒增益調度控制策略保證了變形過程中的穩定性問題。

另一個研究方向則是將飛行器外形變化視作額外的控制輸入，輔助傳統的控制方式，最大程度的發揮變體飛行器的優勢。文獻[8]針對一種可變翼展高超聲速導彈的變形輔助機動控制進行了研究，驗證了將外形變化視作額外控制輸入的優勢。文獻[9]將翼展視為額外控制輸入，并將其解耦為速度、姿態、高度3個回路設計了滑模控制策略，提升了飛行器的機動性能與抗干擾性能。

變形輔助機動控制相比于變形-飛行協調控制能夠在飛行器飛行過程中自主的調節外形以保證最優的氣動外形，所以變形輔助機動控制的問題具有更大的意義。但是由于引入了變形輔助機動，飛行器將變成一個高度耦合的強非線性系統，而飛行器外形變化的方式也直接影響了飛行器模型的復雜程度。所以我們看到目前大部分研究僅關注外形單一變化飛行器的變形-飛行協調控制問題與變形輔助機動控制問題，而更為復雜的外形復合變化變體飛行器的變形輔助機動控制問題則鮮有涉及。

本文中以可對稱改變翼展和后掠角的飛行器為研究對象，研討了基于在線參數辨識的變體飛行器變形輔助機動控制問題。首先給出了可對稱改變翼展和后掠角飛行器的動力學模型，接著基于此給出了變體飛行器的變形輔助機動控制模型。為簡化控制器設計，將模型分為速度回路與姿態回路，設計了固定時間收斂的狀態反饋控制策略。設計了一種在線時變參數辨識算法以針對外形變化導致的氣動系數不確定性以及外界擾動對飛行器的影響進行辨識。然后通過控制分配保證得到的控制指令能夠合理的分配給控制輸入。最后通過仿真驗證了本文中提出方案的有效性。

2 面向控制的變體飛行器變形輔助機動控制模型

本文中采用Navion L-17飛機為飛行器本體，兩側翼展與后掠角能夠對稱變化的變體飛行器為研究對象。定義機翼翼展的變化范圍是原翼展到2倍翼展，機翼后掠角的變化范圍為0～40°。

變翼展變后掠角飛行器面向控制的縱向模型可以表述為如下形式：

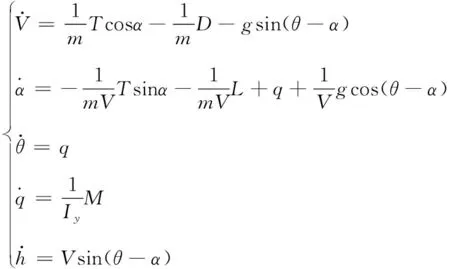
(1)

式中：為速度；為俯仰角；為俯仰角速度；為飛行器質量；為飛行器繞軸轉動慣量；為高度；為油門開度；為推力且推力可表述為下式 ：

=

(2)

式中：=413 N/%為推力系數；為油門開度。

升力，阻力以及俯仰力矩滿足如下關系：

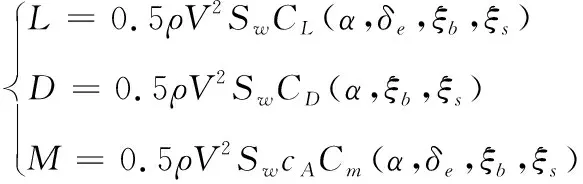
(3)

式中：、、分別為空氣動力產生的升力、阻力以及俯仰力矩；為空氣密度；為機翼參考面積；為平均幾何弦長；為翼展變形率；后掠角變形率分別定義如下：

(4)

式中，為翼展；和分別為飛行器無形變時的翼展以及最大形變時的翼展,且∈[0,1]；為后掠角；和分別為飛行器無形變時的后掠角以及最大形變時的后掠角,且∈[0,1]。升力系數，阻力系數，俯仰力矩系數函數關系定義如下：

(5)

式中：為迎角；為升降舵偏角；=0320 9，=-1019 9，其余氣動導數與零迎角時的氣動系數整理成如下矩陣形式：

[=0=0=0]=[1]

(6)

其中，矩陣系數為：

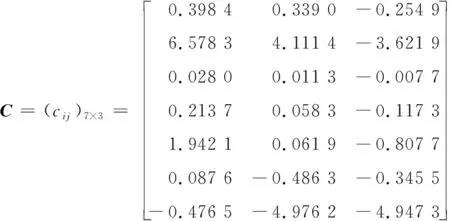
(7)

將翼展變形率，后掠角變形率視為額外的控制輸入，得到如下模型：

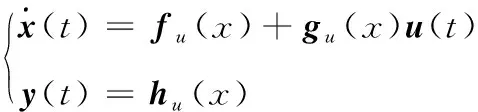
(8)

式中：()=[]為狀態向量；()=[]為輸入向量；()=()=[]為輸出向量。

系統函數()定義如下：

()=[1()2()3()4()5()]

(9)

系統函數()定義如下：

()=[()],=1,2,3,4

()=[()],=1,2,3,4,5

(10)

其中

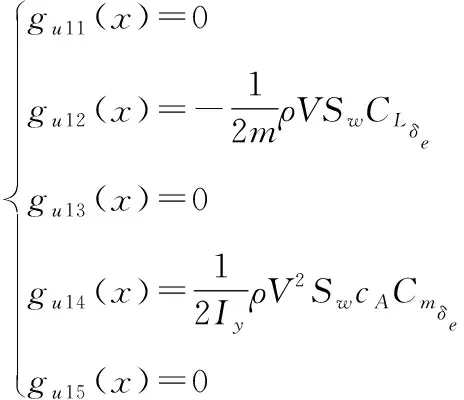
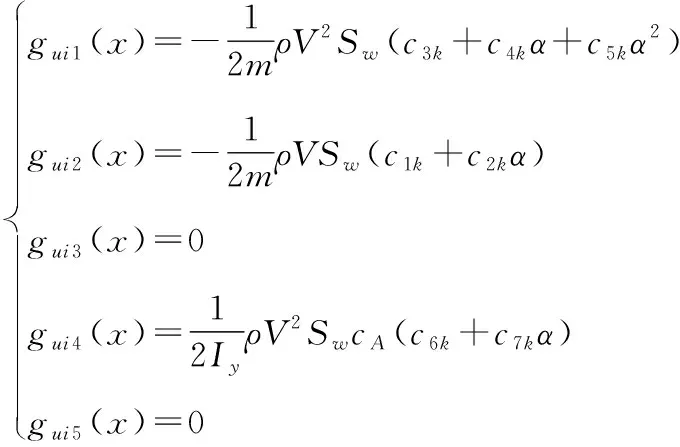
=-1,=3,4

此時可變翼展和后掠角的變體飛行器的變形輔助機動控制模型簡化為一個仿射非線性模型，考慮外形變化導致的氣動系數不確定性和外界擾動對模型的影響將上述模型分為速度回路和姿態回路并給出相對應的含有待辨識參數的形式。速度回路由下式給出：

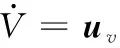
(11)

其中，=1+[1]+Δ1Δ31+Δ41,=1,2,3,4, Δ1、 Δ31、 Δ41為待辨識參數。

飛行器的高度由飛行器的姿態通過跟蹤PID算法得到的進行控制，飛行器的姿態回路由下式給出：

(12)

其中,=4+[4]+Δ4Δ34+Δ44,=1,2,3,4,Δ4、 Δ34、 Δ44為待辨識參數。

3 變體飛行器的變形輔助機動控制

3.1 控制器設計

為了保證飛行器的跟蹤性能，這里我們選用一類固定時間收斂的狀態反饋控制器，控制器的具體設計方案可見文獻[10]，得到速度回路與姿態回路的控制器如下：

(13)

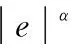
3.2 在線時變參數辨識算法設計

為了得到待辨識參數，以姿態回路為例，首先構造帶有時變參數的非線性系統：

(14)

其中，=[]是狀態向量；()=[Δ4Δ34Δ44]為待辨識參數；()為外界的噪聲以及干擾。已知非線性函數(,)和已知回歸矩陣(,)如下所示：

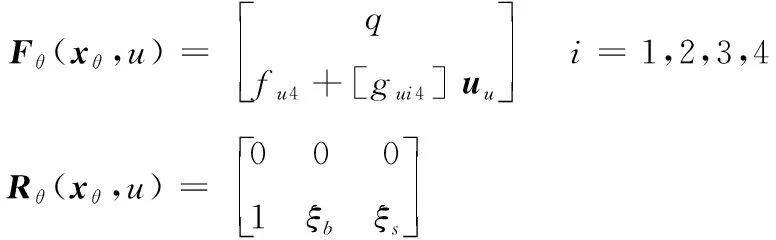
(15)

假設狀態，輸入，未知擾動()，未知參數向量()的導數均有界，(,)與(,)均為和的連續有界函數。

為了得到未知參數向量()與可測或已知變量之間的關系，構造如下濾波器：

(16)

其中，是濾波系數，由上述假設可知，有界并設<,>0。

通過式(16)提出的濾波器作用于系統(14)有：

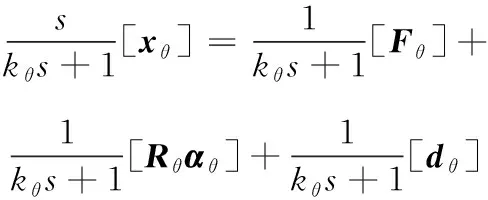
(17)

結合式(16)和(17)并針對(1+1)[]應用交換引理，可以得到：

+-

(18)

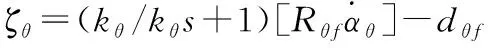
于是我們得到了未知參數向量()與已知變量、、、之間的關系，為了基于這個關系設計自適應律，首先給出如下中間回歸矩陣以及中間向量：

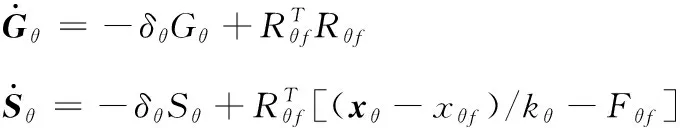
(19)

其中，(0)=0,(0)=0,為大于0的常數，矩陣為正定矩陣。

定義輔助向量1、2如下：

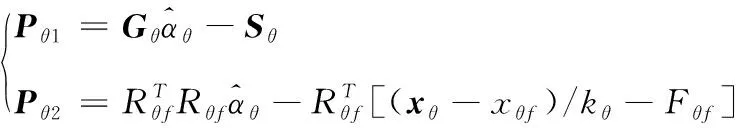
(20)

將式(19)中的中間回歸矩陣與中間向量代入到式(20)中的輔助向量中，能夠得到下式：

(21)

設計估計參數自適應律如下：

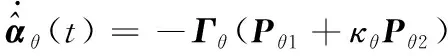
(22)

其中，>0為定常對角學習增益矩陣；>0為正常數，用來平衡快速辨識參數的能力和算法的魯棒性，自適應律的收斂性在文獻[]給出了說明。

3.3 控制分配

為了合理地將得到的控制信號[]分配到控制輸入()=[]中去，需要滿足

=

(23)

其中，

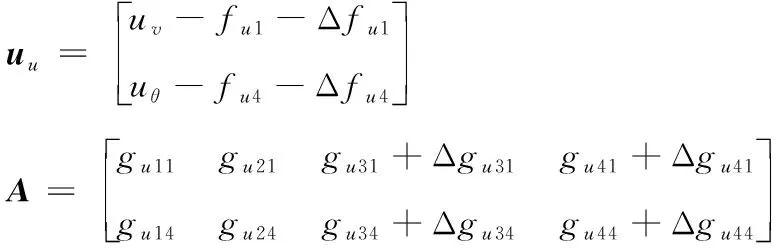
(24)

在進行控制分配的時候我們希望控制輸入在工作點附近變化幅度盡可能小，同時也希望執行器對執行器變化速率進行優化，于是將控制分配問題描述為如下形式：

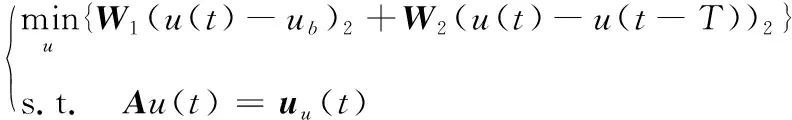
(25)

其中：、為正定的對角權值矩陣；是飛行器平穩飛行的工作點；為數字控制系統的采樣時間。

控制分配式(25)的解為：

=+

(26)

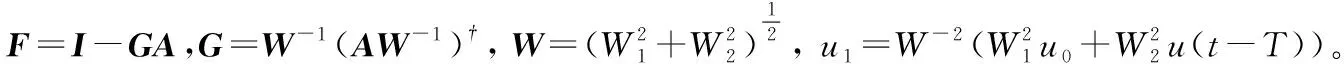
4 仿真驗證

設定飛行指令如下：初始時，飛行器在5 000 m高度以50 m/s的速度勻速飛行，從20 s開始，開始改變飛行的速度與高度；在第50 s時，飛行速度達到60 m/s后保持；第70 s時，飛行器開始減速；80 s時，飛行器達到最低高度4 900 m并保持；第90 s時，飛行器減速到50 m/s并保持現有速度與高度繼續飛行。

在飛行過程中，對飛行器施加20%的氣動系數不確定性以及1 000 N·m的俯仰力矩干擾，其周期均為60 s。變體飛行器的物理參數為：=1 247 kg;=17.1 m;=1.737 m;=4 067.45 kg·m;=1.055 5 kg/m。

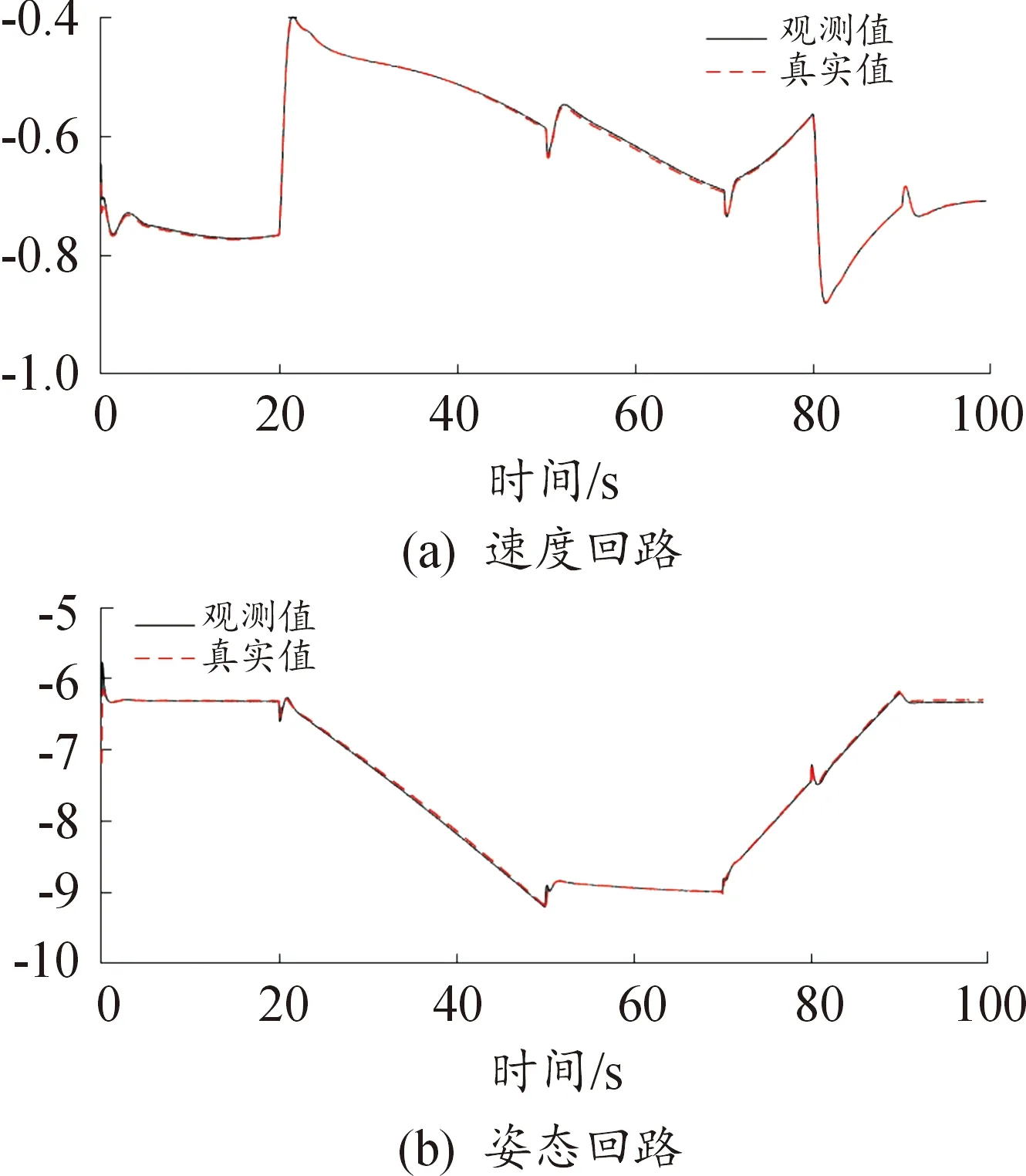
圖1 參數辨識結果曲線

仿真結果如圖2所示。

從仿真結果我們可以看出，本文中提出的在線時變參數辨識在具有外形變化、氣動系數不確定性和外界擾動的情況下很好的辨識出了真值，并結合控制器與控制分配策略達到了預期的控制效果。

圖2 仿真結果曲線

5 結論

本文中以可變翼展變后掠角的變體飛行器為對象，建立了變體飛行器變形輔助機動控制模型。設計了基于交換引理的在線參數辨識自適應律、固定時間收斂的狀態反饋控制器和基于在線參數辨識的控制分配算法。仿真結果表明，在線時變參數辨識可以精確辨識出氣動系數不確定性以及外界干擾對飛行器模型的影響，基于此設計的控制器和控制分配方案達到了預期的控制效果。