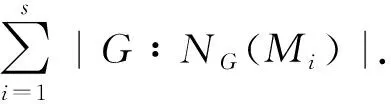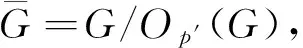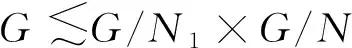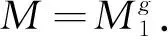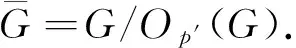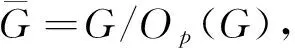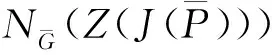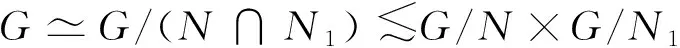有限群的SS-半置換p-子群與p-冪零性①

李彬彬， 鐘祥貴， 張博儒， 盧家寬

廣西師范大學 數學與統計學院， 廣西 桂林 541006

本文所涉及的群都是有限群． 在有限群論中， 利用具有某些性質的子群來研究有限群的結構是人們感興趣的課題[1-4]． 而素數冪階子群相對于其他子群而言， 結構簡單、可控性強， 于是許多學者通過對p-子群的研究， 給出了有限群的p-冪零性的判別條件[5-9]， 例如Frobenius定理[10]． 從Frobenius定理出發， 人們希望運用較少的p-子群給出有限群的p-冪零性的判別條件， 例如Glauberman-Thompson定理[10]．

為了方便起見， 我們給出一些概念． 設H為群G的子群， 如果H與G的每個Sylow子群置換， 則稱子群H為群G的S-置換子群[11]． 文獻[11]引入S-置換的概念之后， 文獻[12]進一步推廣了S-置換性， 提出了SS-置換的概念： 設H為群G的子群， 如果G中存在子群B使得G=HB，H與B的每個Sylow子群都置換， 則稱子群H在群G中SS-置換． 在此基礎上， 文獻[13]提出了SS-半置換的概念： 設H為群G的子群， 如果G中存在子群B使得G=HB，H與B的所有Sylowp-子群置換， 其中素數p滿足(p， |H|)=1， 則稱H是SS-半置換的． 本文主要通過研究較少的素數冪階子群的SS-半置換性對有限群的結構的影響， 給出了有限群G是p-冪零群的兩個充分條件．

引理1[13]設H是群G的SS-半置換子群， 則：

(i) 如果H≤K≤G， 則H是K的SS-半置換子群；

(ii) 如果N是G的正規子群，H是p-子群， 則HN/N是G/N的SS-半置換子群．

引理2[14]設有限群G是π-可分的． 如果Oπ′(G)=1， 則CG(Oπ(G))?Oπ(G)．

引理3[6]設A，B是有限群G的真子群． 如果G=AB， 則G=ABx，G≠AAx對任意x∈G成立．

引理4設N是G的初等交換正規p-子群． 如果N中存在一個子群D， 1<|D|<|N|， 使得N的所有|D|階子群在N中SS-半置換， 則N中存在一個極大子群正規于G．

證令{M1，M2， …，Ms}是N在G中互不共軛的極大子群的集合． 由于N是初等交換p-群， 則Mi是N中一些|D|階子群的乘積． 因為N的|D|階子群都在G中SS-半置換， 則Mi在G中SS-半置換， 即存在B， 使得

G=MiBMiQ=QMi

其中Q是B的任一Sylowq-子群，q≠p． 由Mi是p-子群知Q∈Sylq(G)． 又由Mi

Mi=Op(G)∩MiQ

存在t∈{1， 2， …，s}使得ft=0． 從而Mt?_G．

定理1設G是有限群，P是G的Sylowp-子群，p是奇素數． 如果P的每個極大子群P1在G中都是SS-半置換群， 且NG(P1)是p-冪零的， 則G是p-冪零的．

證假設G是極小階反例， 則G是非p-冪零的．

步驟1Op′(G)=1．

步驟2如果P≤T

根據引理1(i)和NT(P1)≤NG(P1)， 我們容易看到T滿足定理假設， 因此根據G的極小性知T是p-冪零的．

步驟3G/Op(G)是p-冪零的， 且CG(Op(G))≤Op(G)． 實際上，G是p-可解的．

設J(P)是P的Thompson子群， 容易看到P≤NG(Z(J(P)))．

如果NG(Z(J(P)))

進一步， 我們可知Op(G)≠1． 假設N為G的極小正規p-子群． 注意到N≤Op(G)≤P． 如果N=P， 則G/Op(G)=G/P是p-冪零的． 因此可設N

進一步我們假設|P∶N|≥p2， 根據引理1(ii)可知G/N滿足定理假設條件， 再由G的極小性可知G/N是p-冪零的， 從而G/Op(G)是p-冪零的． 進一步可知，G是p-可解的． 再根據Op′(G)=1和引理2可知CG(Op(G))≤Op(G)．

步驟4G=PQ，Q∈Sylq(G)，p≠q．

設q≠p是|G|的素因子． 由于G是p-可解的， 因此根據文獻[15]的定理6.3.5可知， 存在Q∈Sylq(G)使得PQ≤G． 如果PQ

Op(G)Q=Op(G)×Q

再根據步驟3可知

Q≤CG(Op(G))≤Op(G)

矛盾． 因此G=PQ．

步驟5G有唯一的極小正規子群N， 并且Φ(G)=1． 實際上，N=Op(G)．

如果Φ(G)≠1， 則N≤Φ(G)． 然而G/N是p-冪零的， 所以G/Φ(G)是p-冪零的． 進一步可知，G是p-冪零的， 矛盾． 因此Φ(G)=1． 再根據文獻[16]的定理4.5可知Op(G)=N．

步驟6|N|=p， 且存在G的極大子群M， 使得P∩M是P的極大子群．

因為Φ(G)=1， 所以存在G的極大子群M1， 使得NM1． 故G=NM1． 設M′p為M1的Sylowp-子群， 則NM′p是G的Sylowp-子群． 根據Sylow定理可知， 存在g∈G使得

(NM′p)g=N(M′p)g=P

M=〈Mq|Mq∈Sylq(M)，q∈π(M)〉

由于P1是P的極大子群， 所以P1是SS-半置換的． 再根據SS-半置換的定義可知，P1Mq=MqP1對任意的素數q≠p成立． 因為Mp≤P， 所以P1M=MP1． 由M的極大性， 我們可知P1M=G或者P1≤M． 若P1M=G， 則

P=P∩P1M=P1(P∩M)=P1

矛盾． 故P1≤M． 因此我們可以得到|N|=p．

步驟7最后的矛盾．

因為G是p-可解的， 并且Op′(G)=1， 所以根據引理2及N的極小性可知

CG(Op(G))=Op(G)

又由于N=Op(G)是交換群， 因此N=CG(N)． 再根據文獻[16]的定理5.7可得

又因為N是p階循環群， 因此Aut(N)也是循環群． 進一步， 我們可知M也是循環群． 故

M≤NG(P∩M)

因為P∩M是P的極大子群， 所以

P∩M?_PN≤NG(P∩M)

進一步， 根據題設可以得到G=NM≤NG(P∩M)是p-冪零的， 矛盾．

定理2設G是有限群，P是G的Sylowp-子群，p是奇素數． 如果P存在一子群D， 1<|D|<|P|， 使得P中所有|D|階的子群H在P中SS-半置換， 且NG(H)是p-冪零的， 則G是p-冪零的．

證假設定理2不成立， 設G是極小階反例．

步驟1Op′(G)=1．

步驟2P≤T

由于NT(H)≤NG(H)， 且NG(H)是p-冪零的， 因此NT(H)也是p-冪零的． 再根據引理1(i)可知T滿足定理中的假設條件， 故由G的極小性可知T是p-冪零的．

步驟3G/Op(G)是p-冪零的， 且CG(Op(G))≤Op(G)．

步驟4G=PQ，Q∈Sylq(G)，p≠q．

設q≠p，q∈π(G)． 由于G是p-可解的， 因此根據文獻[15]的定理6.3.5可知， 存在Q∈Sylq(G)使得PQ≤G． 如果PQ

Op(G)Q=Op(G)×Q

再根據步驟3可知

Q≤CG(Op(G))≤Op(G)

矛盾． 因此G=PQ．

步驟5G中存在唯一的極小正規子群N， 且G/N是p-冪零的． 實際上，Φ(G)=1，N=Op(G)．

因為G是p-可解的， 且Op′(G)=1， 所以N是初等交換p-群．

首先我們斷言|N|<|D|． 如果|N|=|D|， 則根據定理假設可知G=NG(N)是p-冪零的， 與題設矛盾．

現在我們假設|N|>|D|， 則N的所有|D|階子群在G中SS-半置換． 再根據引理4可知，N中存在的極大子群N2正規于G， 與N的極小性矛盾． 因此|N|<|D|．

如果|P∶D|=p， 則D是P的極大子群． 進一步根據定理1可得G是p-冪零的， 與題設矛盾． 因此|D|>p． 容易驗證G/N滿足定理假設， 則根據G的極小性可得G/N是p-冪零的．

步驟6最后的矛盾．

根據步驟4和Burnsidepaqb定理可得G可解． 進一步根據文獻[16]Ⅲ的定理1.7可得，G中存在極大子群M， 使得M?_G， 且|G∶M|是素數． 如果|G∶M|=q， 則P≤M． 再根據步驟2可知M是p-冪零的． 設M的正規p-補為K， 則KcharM?_G， 由步驟1，K≤Op′(G)=1， 從而

P=M?_GN=Op(G)=P

進一步， 根據引理4可得N中存在G的極大子群N2正規于G， 與N的極小性矛盾． 因此|G∶M|=p． 由于M?_G， 那么根據文獻[16]Ⅱ的命題2.3(6)可得P∩M∈Sylp(M)． 進一步可得P∩M是P的極大子群． 再根據引理1(i)可知P∩M的每個|D|階子群H1在M中SS-半置換，NM(H1)≤NG(H1)是p-冪零的， 從而M滿足定理假設， 由G的極小性知M是p-冪零的，M=(P∩M)×Op(M)， 其中

Op(M) charMM?_G

從而Op(M)?_G． 于是

G=PM=P(P∩M)Op(M)=POp(M)

故G是p-冪零的， 矛盾．