動態步長FOA的PID參數整定方法研究
李 猛,王 垚,劉 義,朱元培
(中國平煤神馬集團尼龍科技有限公司,河南 平頂山 467000)
0 引言
在工業過程控制中, 比例積分微分(proportional integral differential,PID)控制被廣泛應用于各個領域。PID參數整定具有非常重要的作用,關乎整個生產的安全性和產品質量的穩定性。關于PID控制的參數整定和自適應一直是重要的研究方向。傳統的PID控制器參數整定需要豐富的經驗和熟練的技巧,而且無法利用科學的性能準則,不易保證控制效果[1]。隨著人工智能技術的發展,針對PID參數整定逐步發展出一類新型智能優化算法,如蟻群算法、遺傳算法、粒子群算法等將自適應控制、最優控制和預測控制等智能策略引入傳統PID控制,得到許多學者和專家的廣泛關注[2]。果蠅優化算法(fruit fly optimization algorithm,FOA)相比于粒子群算法、蟻群算法和遺傳算法等智能算法,具有參數少、結構簡單且易于實現等優點。在解決實際的工業過程控制問題上,FOA具有廣闊的應用前景。 由于傳統FOA具有早熟和易陷入局部極值等不足,本文將Logistic(t)的變換函數lgt(t)引入FOA中,對該算法改進并用于PID參數整定。仿真結果表明,改進后的算法具有合理性及有效性。
1 PID控制參數的設計
PID控制器包括比例環節、積分環節和微分環節。PID控制系統如圖1所示。

圖1 PID控制系統示意圖
圖1中,ΔKp、ΔKi、ΔKd分別為比例、積分與微分量的加權。
PID控制系統通過輸入值與輸出值的偏差來調節這3個參數,從而達到控制的目的。其控制傳遞函數可表示為[3]:
(1)
式中:Kp為比例系數;Ki為積分時間常數;Kd為微分時間常數。
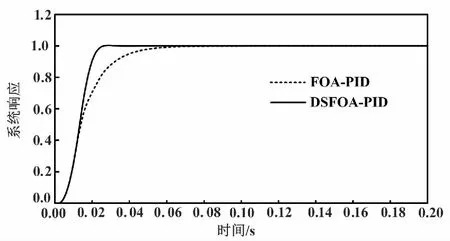
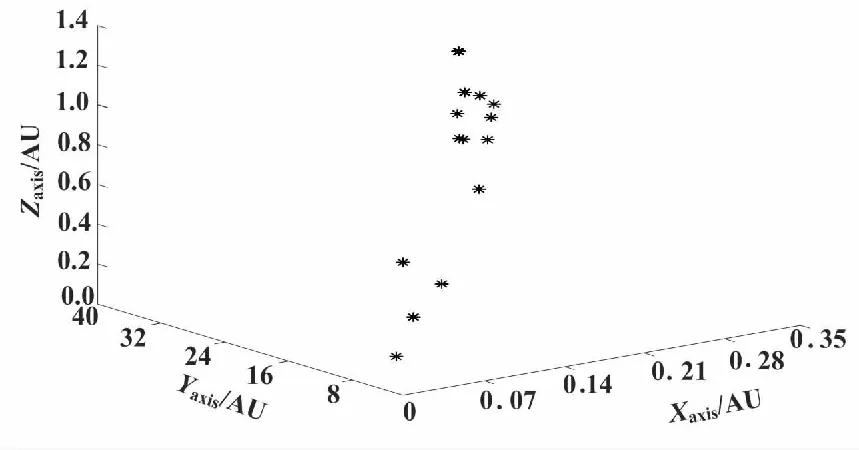
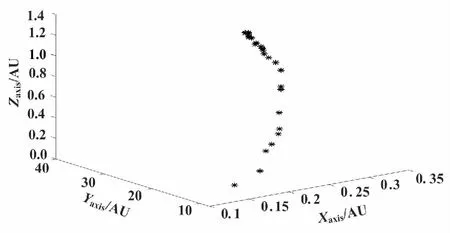
各系數的取值范圍為0 采用FOA[4]對PID控制器參數整定,需要適應度函數綜合評價各項性能指標,選取系統性能評價函數: (2) 式中:w1和w2為權值常數,取值范圍為[0,1];w3為權值,且w3遠大于w1,一般情況下w1=0.999、w2=0.001、w3=100;e(t)為系統誤差,根據迭代過程的動態特性,取其絕對值;u(t)為控制器輸出信號,在適應度函數中引入控制值的目的是防止控制振幅過大;w3|e(t)|被加入目標函數以防止超調[5]。 控制器通過加權可以計算出控制信號,驅動被控對象。一般而言,初始值是在實際應用的取值范圍內隨機生成的。選取被控對象為: (3) 從優化PID控制器參數整定的角度來看,需通過某種算法求出ΔKp、ΔKi、ΔKd這3個參數中最合理的一組值,使得系統表現為最優的性能,輸出良好的階躍響應曲線。 FOA是1種仿生學全局優化演進算法,由潘文超于2011年提出。FOA是利用果蠅在覓食過程中,首先通過嗅覺器官發現食物,然后飛向該區域,再通過視覺尋找食物和伙伴聚集的位置,進而確定最終的食物位置[6]。該算法具有尋優能力強、收斂速度快、可移植性好和可調參數少等優勢。FOA的具體內容主要由隨機初始化、味道濃度判定和迭代尋優這3部分組成[7]。 基本FOA實現流程如下。 ①初始化算法的相關參數。相關參數包括種群規模(即果蠅個體的數量)Spop、最大迭代次數Maxgen以及隨機初始化果蠅群體中心位置Xaxis、Yaxis。 ②果蠅個體在種群中心位置的基礎上隨機選擇方向和距離進行搜索。其中,LValue為果蠅搜索距離和方向的隨機值。 (4) ③計算個體到原點的距離Dj,并將距離的倒數設為個體味道濃度判定值Tj。 (5) (6) ④將Tj代入適應度函數,即可求解出果蠅個體味道濃度值Sj。 Sj=Function(Tj) (7) ⑤找到果蠅群體在本次迭代中味道濃度最優個體的位置,并記錄該個體的濃度值和坐標值(這里以最差個體濃度值為例)。 [bsmell,bindex]=min(Sj) (8) ⑥記錄每次迭代中最佳個體位置,并作為新的果蠅群體位置。其余個體向最佳個體所在位置聚集,并更新最優的濃度值。 (9) ⑦進入迭代尋優,重復執行步驟②~步驟⑤,并判斷味道濃度是否優于前一迭代味道濃度。若是,則執行步驟⑥,直至達到最大迭代次數Maxgen。 根據FOA尋優過程的基本步驟,每次迭代完成后保留最優濃度值和相應坐標作為新的迭代起點。種群中的其他果蠅個體利用視覺向該位置聚集,而后按照搜索步長LValue進行位置的更新[8]。果蠅種群在新位置附近尋優時沒有系統函數對飛行距離和方向進行控制[9]。若步長設置較大,在搜索前期能夠加快全局勘探速率,有利于全局尋優。但在搜索后期,隨著搜索范圍的減小,果蠅十分接近目標源。這時,太大的步長使局部尋優性能下降,需要減少步長進行局部搜索[10]。步長設置太小在搜索前期會使搜索效率下降。因此,固定步長搜索很難平衡全局尋優和局部尋優的精度和收斂速率。 動態步長果蠅優化算法(dynamic step fruit fly optimization algorithm,DSFOA)對PID參數整定的方法,是針對固定步長FOA存在的不足而提出的。DSFOA在搜索初期,先進行全局搜索,在搜索后期隨著迭代次數的增加,搜索范圍逐步減小,進行局部搜索。這樣可以根據尋優的不同階段,使搜索步長隨迭代次數作自適應調整[11]。與FOA相比,DSFOA的改進主要由兩部分構成[8]。 ①確定搜尋動態步長。該步驟是通過將Logistic(t)變換后的函數lgt(t)引入新算法實現的。 (10) 將果蠅搜尋方向和距離的隨機值LValue修正為動態變化的,則: (11) 式中:Gen為當前迭代次數;Maxgen為最大迭代次數。 L′Value可視化結果如圖2所示。 圖2 L′Value可視化結果 圖2中,L′Value呈倒S型。由此可知,迭代前期,以較大的步長進行全局性搜索,加快收斂速度;迭代后期,以較小的步長進行局部性的搜索,從而提高搜索的精度,使得步長可以自適應變化。 ②種群個體坐標更新。種群個體按照式(12)更新,即用式(12)取代式(4)。 (12) 基于DSFOA的PID整定流程如圖3所示。 圖3 基于DSFOA的PID整定流程圖 ①初始化參數包括群體規模Spop、最大迭代數Maxgen和隨機初始化果蠅群體位置Xaxis。其中,每個果蠅的位置由比例、積分、微分這3個控制參數組成Xaxis=[KpKiKd]。在實際的工程應用中,由于果蠅種群的多樣性,設定Kp、Ki、Kd的初始化位置坐標是在相應取值范圍內隨機生成的[12]。 由于Kp的取值范圍為[0,100],Ki、Kd的取值范圍為[0,1],所以設定搜索半徑ωp=1、ωi=ωd=0.1,rand()服從均勻分布,其值在[0,1]之間。 ③根據式(11),隨著迭代次數的增加,保證搜索范圍越來越小。 ④通過目標函數J對解進行評價,并更新局部和全局最優解信息。 按式(9)記錄并保留最佳味道濃度值bSmell與最優果蠅個體位置。 ⑤進入迭代尋優,重復執行步驟②~步驟⑤。若本次迭代的最佳味道濃度值優于上次最佳味道濃度值,將更新、記錄,并判斷當前迭代次數是否大于最大迭代次數。 ⑥通過執行程序,輸出最優個體氣味濃度適應值Sbest以及PID最優參數Xbest(Kp,Ki,Kd)。 在MATLAB 2018a環境下選取二階系統(3)作為控制對象進行仿真,設果蠅種群大小為30、最大迭代次數為100次,輸入為階躍響應信號rin(k)=1.0,采樣時間間隔為0.001 s,對仿真結果進行比較。 系統階躍響應如圖4所示。 圖4 系統階躍響應 由圖4可知,控制系統在輸入單位階躍信號的情況下,DSFOA-PID系統響應的上升時間和調整時間都優于FOA-PID,輸出信號響應速度快,并且在控制過程中系統超調量非常小,有較明顯的控制品質優勢。 氣味濃度適應度函數曲線如圖5所示。 圖5 氣味濃度適應度函數曲線 圖5中,J為根據果蠅群體每輪迭代選定的最優個體與食物源之間的距離,按一定算法得出的數據。由圖5可知,根據lg(t)函數的動態特征,在尋優過程前期DSFOA較FOA搜索范圍更廣,產生誤差較大,適應度函數值更大。隨著迭代次數的增加,搜索范圍迅速減小,適應度函數值相應快速收斂,優化速度超過FOA ,并且在FOA幾乎早熟收斂時DSFOA仍在不停地尋優。這說明DSFOA對防止尋優過程容易過早陷入局部極值的情況具有一定的作用,優化精度優于FOA。 FOA的果蠅群體尋優路徑如圖6所示。 圖6 FOA的果蠅群體尋優路徑 DSFOA的果蠅群體尋優路徑如圖7所示。 圖7 DSFOA的果蠅群體尋優路徑 圖6和圖7中:Xaxis、Yaxis、Zaxis分別對應PID控制器的3個參數Kp、Ki、Kd;軌跡表示每次優化迭代計算出的最優解。隨著迭代次數的增加,預測結果逐漸趨近于目標值。FOA果蠅群體的尋優路徑比較分散。DSFOA的尋優路徑更加集中,有更高的果蠅群體密集度,使解的空間更大,且解的質量得到進一步改善。這有利于平衡局部搜索策略的改良和空間探索能力的提升。由此表明,DSFOA相比于FOA探索質量更高,提升了全局搜索的能力,對解空間探索與開發的能力更強。 2種算法的PID優化參數對比如表1所示。 表1 2種算法的PID優化參數對比 由表1可知,采用DSFOA優化PID控制器,系統的上升時間、調節時間和穩態誤差等參數指標均明顯優于FOA,控制效果更好。由此表明,DSFOA具有更優的控制精度和魯棒性。 為了進一步提高FOA對PID參數整定的控制精度及尋優效率,本文引入Logistic變換后的lgt(t)函數,設計了1種DSFOA對PID參數整定方法,并以二階系統為控制對象進行仿真。仿真結果表明,相比于基本FOA,基于DSFOA的PID控制器參數整定的超調量、調節時間、穩態誤差和上升時間等指標更優,能夠使系統有更好的響應性能和魯棒性。因此,基于DSFOA的PID參數整定為工業控制提供了參考。后續研究將進一步優化該算法的求解性能,使其在實際的工程中得到更合理的應用。
2 FOA及其改進
2.1 基本FOA
2.2 動態步長果蠅算法

3 基于DSFOA的PID參數整定步驟
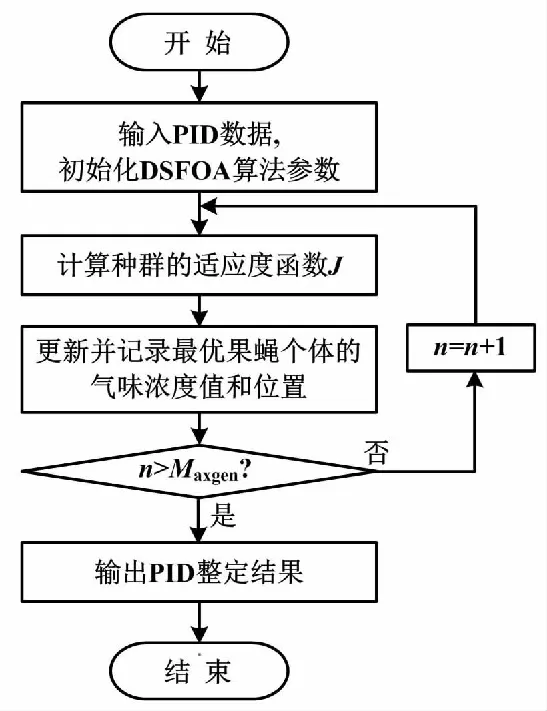
4 仿真試驗與結果分析


5 結論

