行星齒輪機電耦合動力學及其電參數影響機理研究

肖正明， 劉佳偉， 譚加林， 鄭勝予

(昆明理工大學 機電工程學院，昆明 650500)

以電機為動力源拖動齒輪傳動系統，是一種典型的機電耦合系統，被廣泛應用于電動汽車、風力發電機、數控車床等多種機械裝備。隨著電機拖動齒輪系統向大功率、集成化、高功率密度等方向發展，機電耦合作用引起的機械振動問題越發明顯，傳統只關注于電機或機械傳動系統的動力學模型，無法對此狀況下的系統動態響應進行精準預測。因此，有必要考慮機電耦合關系，建立電機-齒輪機電耦合系統才能得出更為真實的系統動態特性，對于電機-齒輪系統動力學設計及狀態監測具有重要意義。

目前針對電機-齒輪系統機電耦合動力學問題，已有廣泛的研究。Khabou等[1]考慮了電機扭矩變化對齒輪激勵，用Newmark法計算了定軸齒輪動力學響應。Girsang等[2]在不同的風和電網條件下進行風力發電機與行星齒輪減速器動力學仿真，得出了系統的瞬態響應。Chen等[3]根據機電系統扭振響應提出了對電機控制策略的改進，從而減小電機的振動。Bai等[4]研究表明機電耦合效應會加劇齒輪的振動。劉長釗等[5]提出了一種可用于分析變速過程的“電機-齒輪傳動系統-滾筒”的純扭轉動力學模型。霍軍周等[6]分析了電機轉矩主從控制和轉速跟隨控制兩種控制方式，對齒輪傳動系統振動響應的影響。于蓬等[7]將減速器和電機整體考慮，基于Maxwell電磁理論得出電磁轉矩激勵，能更好地反映機電耦合系統的振動噪聲特性，并通過試驗驗證了該模型。易園園等[8]面向電機啟動、沖擊載荷等非穩態工況，揭示了電機-多級齒輪系統的扭振信號與定子電流信號的關系。趙心穎等[9]將電氣振蕩轉化為作用在機械系統的動態激勵，得出了電氣控制參數對傳動系統振動的影響關系。朱海燕等[10]對比有、無電磁力矩諧波分量激勵的齒輪箱動力學響應，研究齒輪箱體和電機的振動特性。

綜上所述，大多數研究將電機-齒輪系統動力學模型簡化為純扭轉模型，忽略了時變軸承剛度激勵影響，并且主要關注于電氣系統對傳動系統的激勵作用，較少關注傳動系統振動如何影響電機系統電氣參數變化。本文從動力學角度出發，將時變嚙合、軸承剛度激勵轉化為關于轉角的函數，建立了可適用于不同轉速工況的電機-齒輪機電耦合動力學模型。通過分析系統振動響應及電機定子電流的頻譜對應關系，揭示了傳動系統齒輪、軸承剛度激勵對電機定子電流的調制規律。為進一步電機-齒輪機電耦合系統的動力學設計及狀態監測提供了理論基礎。

1 電機-齒輪系統機電耦合動力學模型

1.1 行星齒輪傳動系統集中參數模型

行星齒輪傳動系統平移-扭轉集中參數模型，如圖1所示。在圖1中，設置有三種類型坐標系用于描述行星齒輪系統：大地坐標系OXY，固定在行星架上并隨其轉動的動坐標系oxy，固定在行星輪上的動坐標系opnxpnypn，n=1,2,…,N，N為行星輪個數，其中opnxpnypn坐標軸軸線與oxy坐標軸軸線相平行。每個元件有x，y，θ三個方向自由度，θc為行星架在大地坐標系OXY中的轉角，θs及θr分別為太陽輪、內齒圈在動系oxy中的轉角，θpn為行星輪在動系opnxpnypn中的轉角。Ts為作用在太陽輪的驅動力矩，Tc為作用在行星架上的負載力矩。φn為第n個行星輪在oxy中的位置角，φn=2π (n-1)/N。

在動坐標系oxy中行星輪系可視為定軸輪系，由此可確定齒輪嚙合變形δspn及δrpn

(1)

式中，espn(θpn)及erpn(θpn)分別為太陽輪-行星輪、行星輪-內齒圈之間的齒輪綜合嚙合誤差，可寫為以行星輪轉角為自變量的正弦函數，其幅值由齒輪加工精度決定。

進一步，考慮時變嚙合剛度影響，并將嚙合阻尼視為定值[11]，可計算出動態嚙合力為

(2)

考慮構件切向加速度引起影響，應用非慣性系的牛頓定律[12]建立行星齒輪傳動平移-扭轉動力學方程。太陽輪、內齒圈、第n個行星輪(n=1,2,3)及行星架的運動微分方程依次如式(3)～式(6)所示

(3)

(4)

(5)

(6)

式中，δpnx，δpny，δpnt分別為行星輪與行星架在x，y及切向方向的相對位移，可由坐標系oxy與坐標系opnxpnypn的位置關系計算得出

(7)

1.2 電機-齒輪系統機電耦合模型

在dq坐標系中建立異步電機動態模型：使用Park變換將電機定子三相電壓轉化到兩相旋轉dq坐標系中，異步電機電氣參數也折算到dq軸等效電路模型中，對應的Park變換公式、電壓方程、磁鏈方程和電磁力矩方程如式(8)～式(11)所示[13]

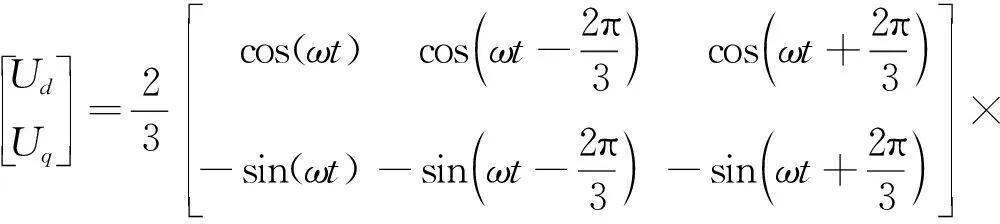
(8)

(9)

(10)

Te=1.5ne(ΨdsIqs-ΨqsIds)

(11)

式中：下標d，q分別為d，q軸上分量； 下標s，r分別為電機定子、轉子；U，I，R，L，Ψ分別為電壓、電流、電阻、自感、漏感及磁鏈；Lm為定轉子互感；ne為電機磁極對數；ω為dq坐標系角速度；ωr為電機電角速度，ωr=neωM，ωM為電機轉子角速度。

如圖2所示，電機轉子軸與太陽輪相連，行星架軸與負載轉子相連。在大地坐標系OXY中太陽輪轉角為(θc+θs)，由此電機轉子及負載端動力學方程為

(12)

以電機與行星齒輪系統的力學關系，建立機械系統與電氣系統的聯系，結合式(3)～式(12)可建立電機-齒輪系統機電耦合動力學方程為

(13)

式中：X為廣義自由度；M，C，G，K，Kt，Ka，T，E分別為廣義質量矩陣、總體阻尼矩陣、陀螺矩陣、總體剛度矩陣、向心剛度矩陣、切向剛度矩陣、外部激勵力矩向量及嚙合誤差激勵向量；U，R，I，Ψ，ω，L分別為電壓向量、電阻矩陣、電流向量、磁鏈向量、角速度矩陣及電感矩陣。

建立了包含力-電-磁三種物理方程的動力學模型，如式(13)所示。第一個方程是多自由度受迫振動的力學方程，其在內部受齒輪時變嚙合剛度與嚙合誤差激勵，在外部受由電磁力矩Te及負載TL激勵；第二個方程代表電機等效電路模型，其由電機電氣控制系統及轉子轉速共同決定；第三個方程用于計算動態磁鏈；第四個方程用于計算動態電磁力矩。由此建立了電機-齒輪系統機電耦合模型。

2 時變剛度求解

2.1 時變嚙合剛度求解

本文使用文獻[14]提出的改進能量法計算時變嚙合剛度，該方法考慮了較為真實的過渡曲線方程，提高了嚙合剛度的計算精度。行星齒輪系統主要參數如表1所示。

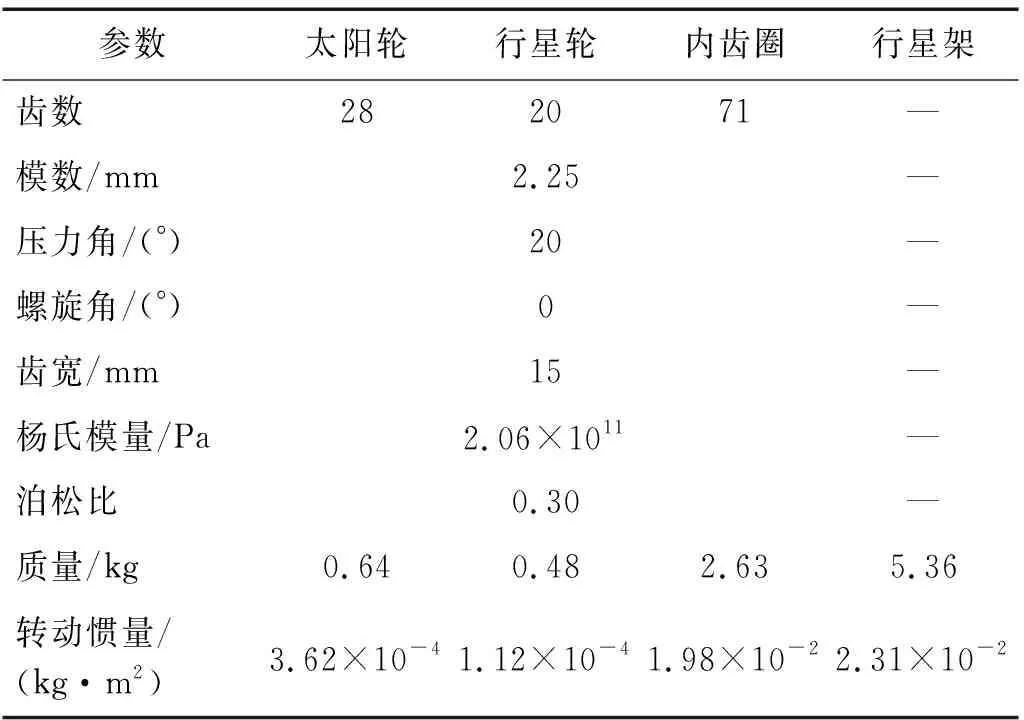
表1 行星齒輪傳動系統主要參數Tab.1 The main parameters of the planetary gear

受電氣控制系統影響，傳動系統轉速具有時變性，使用角度表示時變嚙合剛度，比時間表示更具優勢。采用角度表示時變剛度之后，不需要系統轉速信息，使得模型在不同轉速工況或非穩態工況也具有適用性。進一步，將時變嚙合剛度展開傅里葉級數形式，如式(14)所示

(14)

式中：a，b為傅里葉級數各項系數；l為諧波次數；γn為嚙合初相位；γr為內嚙合相位差，其取值與行星輪齒數有關，齒數為奇數時取為0，齒數為偶數時取為π。

在保證計算精度的情況下為減少計算量，使用8階傅里葉級數擬合由改進能量法得出的時變嚙合剛度。太陽輪-行星齒輪1時變嚙合剛度kspl計算結果及級數擬合對比如圖3所示。8階傅里葉級數各項系數如表2所示。

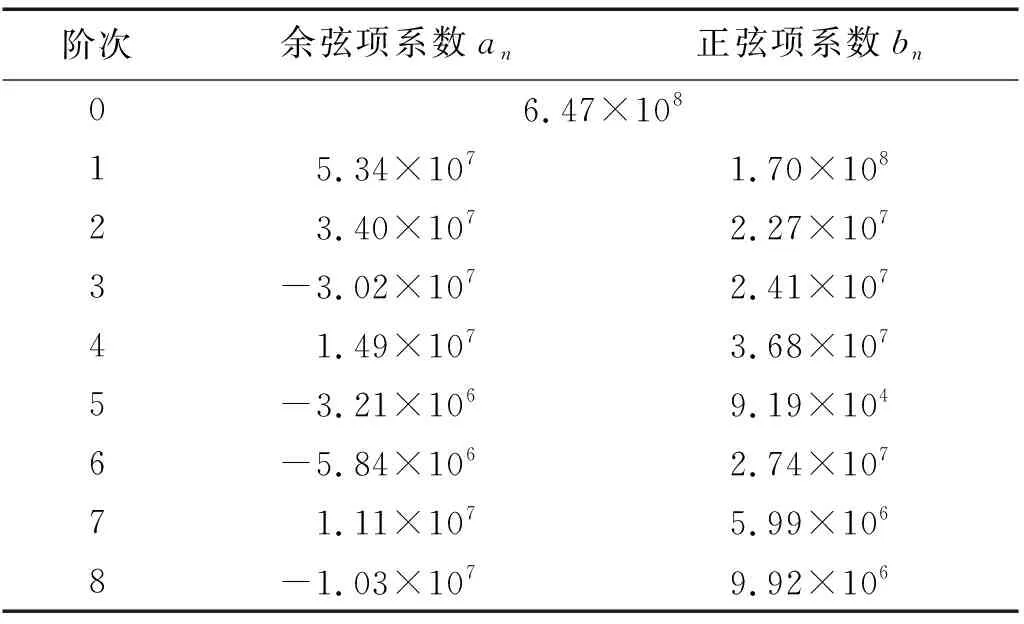
表2 傅里葉級數各項系數Tab.2 The Fourier series coefficients

2.2 太陽輪處時變軸承剛度求解

基于赫茲接觸理論建立軸承分析模型計算時變軸承支承剛度[15]，軸承分析模型如圖4所示。為簡化計算，模型假設軸與內圈無相對滑動，外圈與箱體剛性連接，滾子與滾道之間不發生相對滑動，不計軸與內圈之間的游隙，在運動期間滾子始終為等距排列，滾子只在受到壓縮時才產生變形。在該假設下，軸承的變形主要由滾子與軸承內外圈之間的接觸變形組成。

第i個滾子的接觸變形可以表示為

(15)

式中：xb，yb分別為軸承內圈圓心在x，y向的位移，即為內圈與外圈在的相對位移；φi為軸承滾子位置角；Nb為軸承滾子個數；θz為軸承內圈的轉角。

滾子形狀為球形，根據赫茲接觸理論，由接觸變形產生的動態軸承力為

(16)

式中：Kc為赫茲接觸剛度，由軸承材料、接觸形狀決定；H(δbi)為海維賽德函數用于判斷滾子i是否發生接觸變形，當δbi為正時為1，否則為0。

為充分考慮振動響應對動態軸承力的影響，并與行星齒輪動力學模型直接地聯系起來，將軸承力轉化為軸承剛度計算，軸承支承剛度定義為

(17)

通常支承剛度矩陣主對角元素遠遠大于非對角元素，可將非對角元素忽略[16]，軸承在xb，yb方向上的支承剛度可表示為

(18)

在穩定工況下，振動位移對軸承滾子接觸變形影響較小，xb，yb取為定值，太陽輪軸承內外圈的直徑分別為40 mm和80 mm，滾子數目9，滾子赫茲接觸剛度Kc為4.2×108N/m，利用式(18)可計算出其時變軸承剛度。在穩定工況下太陽輪x方向軸承支承剛度變化如圖5所示。

3 傳動系統振動-電機電流作用關系

在式(12)中電機軸變形產生的力為作用在電機轉子上的負載記為Td。受齒輪系統以及負載波動等動態激勵，假設Td波動頻率為fd，受Td激勵下電機轉子角速度、電磁力矩動態響應可寫為

(19)

在dq坐標系中，定義d軸與轉子磁鏈Ψr方向一致，這樣dq坐標系旋轉速度與磁場旋轉速度相同，電機內部磁場相對位置固定。此時，ABC三相電流在dq坐標系中分解為沿d軸方向的勵磁電流分量Ids及沿q軸方向的轉矩電流分量Iqs，兩分量相互獨立，由此電磁力矩可簡化為[17]

(20)

在式(20)中，轉子磁鏈Ψr由勵磁電流分量Ids與電機參數決定，與定子轉矩電流分量Iqs無關，當電氣參數為常數時Te與Iqs成正比，此時若Te波動則Iqs也會以同頻率進行波動。Park變換屬于線性變換，Iqs波動時三相電流也發生對應頻率的波動，導致Ids與Iqs同頻率波動。由此Td以fd為頻率波動時，dq坐標系中電流分量可表示為

(21)

在異步電機中磁場旋轉速度等于電機定子電流變化速度，由此dq坐標坐標系轉速ω=2πfe，fe為電機定子電源頻率。電流Park逆變換公式可寫為

(22)

將式(21)代入式(22)中，可求出定子電流，并使用三角函數積化和差公式進行整理，可得定子A相電流如下

(23)

由式(23)可以看出，在Td激勵下定子電流特征頻率除了電源頻率fe之外，還出現了fe-fd，fe+fd與激勵頻率有關的頻率成分。在實際中激勵頻率fd常常大于電流頻率fe，由于余弦函數為偶函數，進一步地邊頻成分可表示為|fe±fd|。傳動系統振動給電機轉子帶來動態激勵，造成電機軸負載的波動，從而電流頻率會受到機械部分頻率調制作用，產生相應邊頻。

4 電機-齒輪系統機電耦合仿真模型

4.1 機電耦合仿真模型搭建

使用MATLAB/Simulink求解機電耦合模型：首先，使用Simulink模塊搭建異步電機及其電流滯環控制模型；其次，使用S-Function函數建立電機-齒輪系統動力學方程，電磁力矩等外部激勵作為輸入系統；最后，異步電機輸出電磁力矩作用于動力學系統，由動力學系統計算出電機軸轉速而后輸入電機系統，完成機電耦合模型的建立。Simulink仿真模型搭建如圖6所示。行星齒輪主要參數如表1所示，電機主要參數如表3所示。

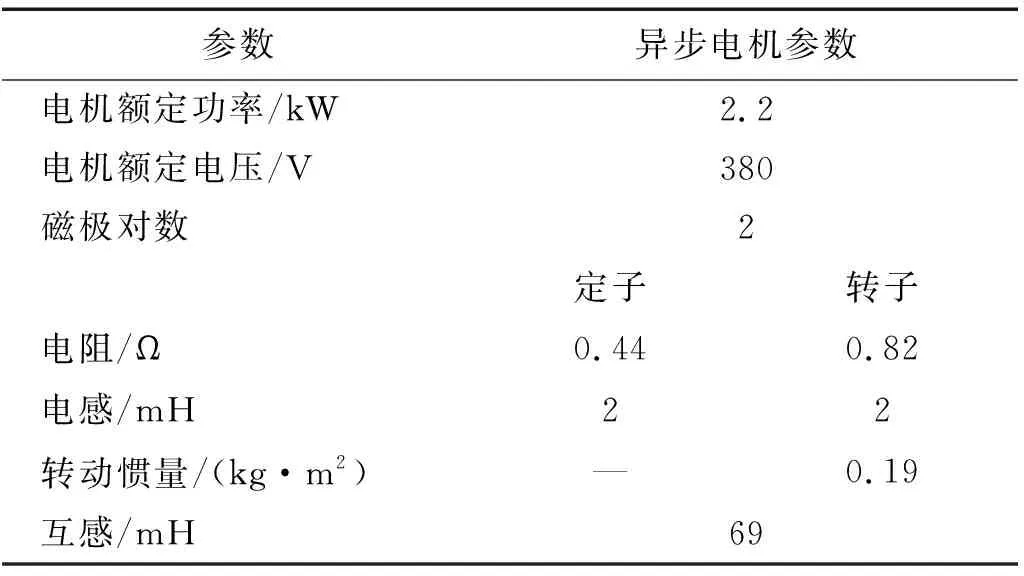
參數異步電機參數電機額定功率/kW2.2電機額定電壓/V380磁極對數2定子轉子電阻/Ω0.440.82電感/mH22轉動慣量/(kg·m2)—0.19互感/mH69

4.2 動力學仿真結果與驗證

在仿真中設置電機目標轉速為1 000 r/min，負載轉子處添加恒定負載為30 N·m，選用ode4龍格庫塔固定步長算法對電機-齒輪系統進行求解。在該工況下，仿真得出的太陽輪x，y向振動加速度，并投影到大地坐標系Y向，其時頻響應如圖7所示。

本文行星齒輪模型參數與文獻[18]相同，且在相同工況下，仿真得出的振動加速度響應的時域幅值，特征頻率分布與曹金鑫的試驗結果相符，驗證了本文動力學模型的有效性，為后續定子電流響應分析提供了可靠的動力學模型。

5 傳動系統對定子電流響應影響分析

5.1 齒輪時變嚙合剛度對定子電流響應的影響

為研究齒輪時變嚙合剛度對定子電流響應的影響，同時為時變軸承剛度作用下的仿真結果提供對照，將行星齒輪系統中的軸承剛度取為常數。電機目標轉速設置為600 r/min，負載轉子處添加恒定負載為30 N·m，系統響應穩定時，對應電流頻率fe1為21.2 Hz，行星齒輪系統嚙合頻率fm1=Zpωp為202.1 Hz。

電機軸扭振速度頻譜如圖8(a)所示，電磁力矩頻譜如圖8(b)所示，電機定子A相電流頻譜如圖8(c)所示。動態嚙合力作用在齒輪的轉動上，是電機軸扭振的主要激勵源，所以在電機軸扭振速度頻譜圖8(a)中，其主要峰值由嚙合頻率fm1及其倍頻組成；電機軸的扭振直接作用于電機轉子，其作用關系如式(12)所示，扭振產生的力矩引起電磁力矩的同頻率響應。同受電流影響，在圖8(b)中還出現了由電源頻率及PWM發生器產生的電流頻率；在定子電流頻譜圖8(c)中，其峰值主要為電流頻率，同時也包含與機械振動頻率相調制頻率為|fe1±nfm1|的峰值。由于電機轉子相對較大的轉動慣量及電機定子繞組產生的電感，使得電機系統對高頻激勵不敏感，具有低通濾波的性質，導致從電機軸扭振到電磁力矩再到定子電流，高頻部分幅值逐級衰減。

5.2 太陽輪處時變軸承剛度對定子電流響應的影響

為研究太陽輪處時變軸承剛度對定子電流響應的影響，在引入太陽輪處的時變軸承剛度激勵影響，并進行仿真。仿真工況設置與5.1節相同，該條件下時變軸承剛度頻率fb1=Nbωs為90.6 Hz。

電機軸扭振速度頻譜如圖9(a)所示，電磁力矩頻譜如圖9(b)所示，電機定子A相電流頻譜如圖9(c)所示，電機定子A相電流頻譜0～500 Hz局部放大如圖9(d)所示。引入時變軸承剛度后，齒輪x，y方向的振動響應受其激勵包含了時變軸承剛度頻率，在計算動態嚙合力時，齒輪時變嚙合剛度與該振動響應相乘，出現了齒輪嚙合頻率與時變軸承剛度頻率在頻域上的卷積，所以與圖8(a)相比，圖9(a)中出現|n1fm1±n2fb1|的頻率調制，n1，n2分別為嚙合剛度、軸承剛度的諧波次數；同時也可以看出相對于嚙合剛度，時變軸承剛度引起的激勵較小。|n1fm1±n2fb1|以與4.1節中所述相同的方式傳遞到電機系統如圖9(b)及圖9(c)所示。在定子電流頻譜中，|n1fm1±n2fb1|進一步與電源頻率fe1產生調制，出現|fe1±(n1fm1±n2fb1)|的頻率成分。由于軸承剛度引起的激勵本身幅值較小，并且電機系統帶有低通濾波的效果，所以軸承剛度引起的頻率成分在高頻部分難以觀測，忽略高次諧波成分重點觀察0～500 Hz低頻部分響應如圖9(d)所示，電流上體現出了軸承剛度頻率而且低頻部分的幅值更明顯。

5.3 不同轉速下定子電流響應

為研究不同轉速下的電流響應，設置電機目標轉速為1 000 r/min，其他仿真條件設置與5.2節相同，在此對系統進行仿真。該工況下，電流頻率fe2為35.2 Hz，齒輪系統嚙合頻率fm2為336.6 Hz，時變軸承剛度頻率fb2為150.6 Hz。

對比600 r/min及1 000 r/min時電機系統動態響應，在不同轉速下，電機軸扭振速度頻譜如圖10(a)所示，電機定子A相電流頻譜如圖10(b)所示。由于負載不變，在不同轉速下行星齒輪傳動系統動態嚙合力頻率不同，而幅值大致相同，動態嚙合力激勵作用于扭振，所以在圖10(a)中，不同轉速下的嚙合頻率nfm1與nfm2所對應的峰值大致相同；在轉速為1 000 r/min時，轉速較高齒輪水平及豎直方向振動響應較大，所以軸承引起的邊頻具有更大的幅值。轉速變化導致特征頻率偏移也反應在了定子電流頻譜中，與扭振頻譜不同的是，由于負載不變轉速升高系統功率升高，所以fe2的峰值大于的fe1的峰值，其次電機系統帶有低通濾波的性質，|fe2±fm2|頻率較高其幅值小于|fe1±fm1|處幅值。轉速不同時，引起電源頻率、嚙合頻率及軸承頻率的變化，造成對應特征頻率在定子電流頻譜上的偏移，由此可通過定子電流頻率響應監測行星齒輪傳動系統及其齒輪、軸承部件的運行工況。

6 結 論

本文建立了包含控制系統、電機系統、及行星齒輪傳動系統的機電耦合動力學模型，并對動力學模型進行了數值仿真求解綜合分析得出以下結論：

(1) 受機械振動激勵，定子電流頻率與機械振動激勵頻率在頻域上產生卷積，產生與機械振動頻率有關的邊頻成分。

(2) 齒輪時變嚙合剛度引起的時變嚙合力直接激勵扭振，所以其在定子電流頻譜上體現為電源頻率與嚙合頻率的頻率調制。

(3) 時變軸承剛度通過作用于齒輪水平與橫向振動，從而影響動態嚙合力的計算，間接地作用在扭振上，所以在定子電流頻譜中，時變軸承剛度頻率首先與嚙合頻率產生頻率調制作用于扭振，再與電源頻率相卷積作用于電流上。

(4) 在不同轉速工況下，電源頻率、嚙合頻率及軸承頻率的變化，引起定子電流頻譜中對應的特征頻率偏移，為監測系統運行狀態提供了依據。