應用變分模態分解和隨機森林特征選擇算法的揚聲器異常聲分類

周靜雷， 周 智， 崔 琳

(西安工程大學 電子信息學院，西安 710600)

揚聲器被廣泛的應用在手機、耳機、智能音箱、家庭影院、筆記本電腦等設備上，其品質的好壞直接決定人們的音效體驗。因此無論在揚聲器的研發、制樣及生產環節，都需要對揚聲器進行異常聲檢測。有無異常聲已是揚聲器的關鍵必檢特性之一。而檢測的準確性、時效性和自動化，對于揚聲器生產而言，具有重要意義[1]。

揚聲器異常聲檢測一般由激勵及響應捕捉、響應信號的特征提取、特征選擇以及分類構成。由于揚聲器的異常聲信號是非線性非平穩信號[2]。對于此類信號，一般采用時頻域分析的方法，以提取最佳的信號特征[3]。特征提取的方法主要有高階諧波失真(high-order harmonic distor-tion)[4]、短時傅里葉變換(short-time Fourier transform，STFT)[5]、小波包分解(wavelet packet decomposition，WPD)[6]、經驗模態分解(empirical mode decomposition，EMD)[7]。高階諧波失真提取法需要有經驗的工程師設置合理的門限；STFT分辨率單一，依賴選擇的窗函數，缺乏自適應性[8]；WPD雖然可以同時分解低頻與高頻信號，但是其受小波函數、信號采樣頻率等影響，存在能量泄露問題[9]；EMD分解具有良好的自適應性，但是易出現模態混疊和端點效應[10]。VMD分解[11]相比EMD，有更好的抗模態混疊和降噪性能[12]。VMD分解被廣泛的應用在機械故障診斷[13]以及心音信號[14]處理，本論文在文獻[15]的研究基礎上，著重討論特征選擇及不同分類方法在異常聲檢測中的應用。

特征選擇[16]是為了篩選出最有效的特征、降低特征空間維數以達到最高的分類精度。依據評價方式，可分為過濾式(Filter)和封裝式(Wrapper)[17]兩種。Filter式采用某種評價準則或搜索策略進行特征子集選擇，計算效率比較高[18]，但不能與具體的分類器結合，特征子集的冗余較高、分類效果較差；Wrapper式則直接以分類性能的好壞作為特征子集的評價標準，在合理的學習算法中得到的較好的特征子集和分類性能[19]。隨機森林(random forest，RF)是一種典型的Wrapper式特征選擇算法，其內置了特征重要性評價機制，在高效特征選擇的同時，還能保持著較好的選擇效果。為了選取最優的特征選擇效果，提出了基于隨機森林結合遞歸特征消除[20](random forest and recursive feature elimination,RF-RFE)的特征選擇算法。

揚聲器異常聲檢測中，通常采用特征距離公式、BP神經網絡[21]、支持向量機(support vector machine，SVM)[22]等方法對異常聲進行分類。但是特征距離公式通常只能檢測出是否有異常聲，不能判斷異常聲的類別；SVM雖然可以進行多分類，但其依賴選擇的核函數，消耗時間較長。RF是一種集成模型，相比SVM有著更強的魯棒性和分類效果，適用于多分類問題，本文選用RF作為分類器。

為了更好提取揚聲器異常聲最佳的信號特征、有效提高診斷系統分類性能，本文提出了基于VMD與RF-RFE的揚聲器異常聲分類方法。首先，對揚聲器單元的聲響應信號進行VMD預分解，根據中心頻率相近法確定VMD分解后的模態K的個數，之后以確定的K值對揚聲器單元聲響應信號進行VMD分解，提取每個模態的時、頻域特征構成原始特征數據集；其次使用RF-RFE模型對原始特征集進行特征選擇，確定最優特征個數以及最優特征子集；最后將得到的最優特征子集輸入至RF算法中進行判斷，輸出分類結果。試驗表明本文提出的方法能夠有效地診斷揚聲器的故障類型。

1 基于VMD的特征提取

1.1 VMD基本原理

VMD以各模態帶寬最小和原則，采用非遞歸方式搜尋變分模型最優解。其實質為如式(1)所示的變分約束問題的求解

(1)

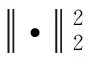
其具體求解步驟為：

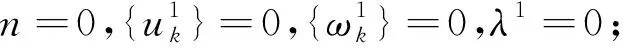
步驟2更新迭代次數n=n+1；

步驟3fork=1∶K

(2)

(3)

步驟4采用對偶上升法，更新

(4)

式中:n+1為迭代次數；τ為噪聲容限，一般情況下τ=0。

步驟5重復步驟1～步驟4,直到滿足收斂條件

(5)

式中，ε為收斂精度，大小通常為10-6。

1.2 特征提取

VMD分解之后，分別求得各模態波形因子(Es)(X1)、波峰因子(Ec)(X2)、脈沖因子(Ed)(X3)、最大值(X4)、平均值(X5)、標準差(X6)、均方根值(X7)、方差(X8)、最小值(X9)、峰峰值(X10)、均方幅值(X11)、平均幅值(X12)、峭度(Eku)(X13)、偏度(Esk)(X14)、能量熵(Eentropy)(X15)、排列熵[23](X16)、過零點數(X17)、VMD分解中心頻率(X18)以及VMD-Hilbert時頻熵(Et)(X19)構成原始的特征向量。對長度為N的模態分量ui，部分特征的計算公式為

(6)

(7)

(8)

(9)

(10)

(11)

(12)

2 基于隨機森林的特征選擇算法

2.1 隨機森林基本原理

隨機森林是一種集成算法，由多顆子樹構成，每一顆子樹均通過Bootstrap抽樣方法產生，每一顆子樹的分布相同且獨立，最后由分類樹投票的多少決定新數據的分類。隨機森林算法不僅具有模型簡單、分類效果好的特點，同時其魯棒性強，不易過擬合，因此被廣泛的應用在各種分類、預測以及特征選擇等相關問題當中[24]。

2.2 隨機森林特征選擇算法

利用RF-RFE進行特征選擇包含特征重要性計算和遞歸特征消除兩個部分。特征重要性計算是RF內嵌的功能，以袋外(out-of-bag，OOB)數據分類準確率的變量為評價準則。

假設有bootstrap樣本k=1,2,…，K,K表示訓練樣本的個數，每個樣本有N個特征，特征重要性排序的計算步驟如下：

步驟1初始化k=1，創建決策樹Tk;

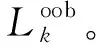
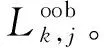
步驟4對于k=2,3,…,K重復步驟1～步驟3。

步驟5特征Xj的重要性度量Pj通過式(13)計算

(13)

步驟6對Pj降序排列，得到特征重要性排序。

將排序好的特征輸入至遞歸特征消除算法中，反復構建模型，選出得分最高的特征放到最優特征子集中，之后剩余的特征重復上述過程，直到遍歷所有特征后停止，最終得到最佳的特征數量和最優的特征子集。

3 揚聲器異常聲分類

本文提出的分類方法分為 VMD信號分解及特征提取、基于 RF-RFE的特征選擇和基于RF的分類 3個階段，如圖1所示。

第一階段，對采集到的揚聲器響應信號進行VMD分解，得到K個模態分量，分別提取每個模態的時域及頻域特征，構成原始的特征數據集；

第二階段，將原始的特征數據集輸入至RF中，得到特征重要性排序，再通過RFE得到最佳的特征數量和最優的特征子集，將特征子集劃分為訓練樣本和測試樣本；

第三階段，使用訓練樣本集訓練RF分類器，之后使用測試樣本集對訓練所得的RF模型進行測試，最后輸出分類結果。

4 試驗分析

4.1 試驗數據采集

試驗采用諧振頻率為180 Hz的3580-3型彩電揚聲器單元，阻抗為6 Ω，額定功率為10 W，該型號揚聲器異常聲多發于低頻段，揚聲器單元在其諧振頻率的附近振幅將達到最大，更容易激發出潛在的異常聲。在進行揚聲器單元測量時，使用高頻到低頻的掃描方式可以有效減少其穩定時間[25]。因此，本次試驗采用1 800～20 Hz的連續對數掃頻信號，其時域圖如圖2所示，由高頻到低頻的掃描方式激勵被測揚聲器單元，激勵時長為1 s，激勵電壓為1 V。本次試驗所采用的平臺如圖3所示。

本次試驗共測試了良品、異物、缺膠、碰圈、脫盆架、音小、紙盆聲7種狀態下的揚聲器單元，每種狀態下的揚聲器單元各14個。其中異物指揚聲器單元中存在鐵屑等松散顆粒，缺膠指防塵帽或壓邊缺膠，碰圈指音圈變形或支架不平導致與磁體發生碰撞，脫盆架指盆架安裝松動，音小指支片沾有膠水或者磁鋼未充磁，紙盆聲指紙盆破裂變形等。對上述七種揚聲器單元狀態，分別貼標簽為1、2、3、4、5、6、7。對每個揚聲器單元進行5次測試，減小隨機信號對數據影響的同時也增加了樣本的數量。

4.2 VMD分解

本試驗中所用消聲箱體積較小，在低頻段，箱內聲場接近壓力場，如圖4、圖5分別為合格揚聲器在自由場和消音箱條件下聲響應信號的頻域圖，采樣時間為1 s，采樣頻率為44.1 kHz。對揚聲器信號進行VMD分解前需要確定模態數K。本文采用觀察中心頻率法來確定K值，不同K值的中心頻率如表1所示。

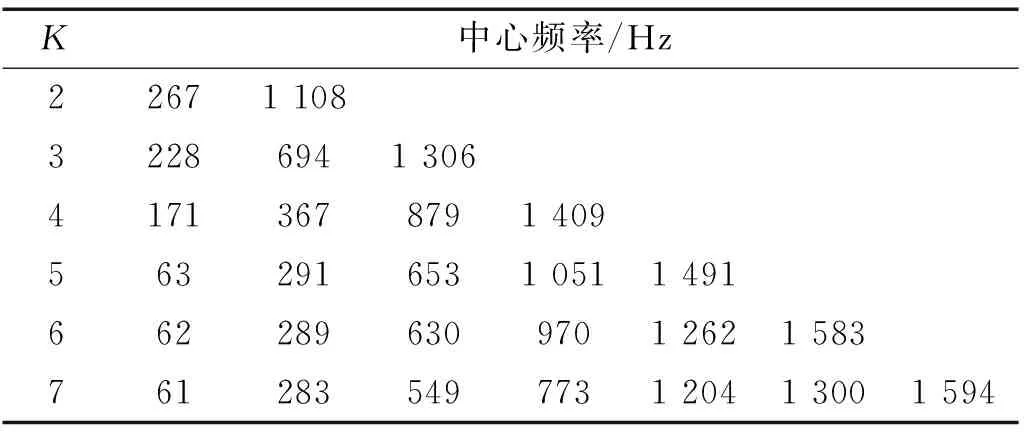
表1 不同K值對應的中心頻率Tab.1 Center frequency corresponding to different K values

當K=7時，出現中心頻率為1 204 Hz和1 300 Hz兩個模態，認為其中心頻率較近，出現過分解。因此選擇K=6，同時α設定為2 000，此時可以取得理想的分解效果。如圖6、圖7分別為VMD分解所得的揚聲器在不同狀態中各模態的時域和頻域圖。

由圖6、圖7可以看出， VMD分解不僅能將合格揚聲器單元的聲響應信號分解到各個頻帶中，同時也能將各種異常揚聲器單元的聲響應信號分解到各個頻帶中，每一個頻帶對應著一個模態分量，并且各頻帶的頻率中心未出現交叉和過分解，且不存在混疊現象，充分體現出VMD分解的優勢。

4.3 特征選擇

針對上述7種揚聲器聲響應信號，將其分解為6個模態分量，分別提取每個模態的X1-X18特征，以及VMD-Hilbert變換后的X19特征。由此得到109維原始特征向量，維數較高，可能存在冗余特征，影響后續分類結果，因此利用RF-RFE模型對其進行特征選擇，篩選出具有較高鑒別力的特征。由于RF中受決策樹數量(T)、樹的最大深度(D)、每棵樹每個節點分裂所需最小樣本數(S)影響較大，因此首先使用隨機搜索策略[26]對其進行尋優，尋優范圍及結果如表2所示。

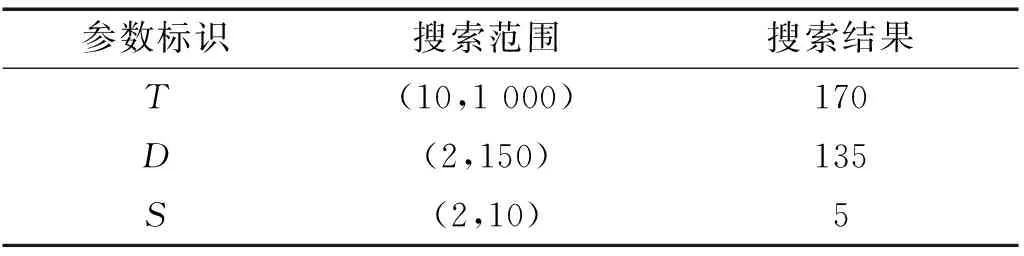
表2 隨機森林參數優化Tab.2 Random forest parameter optimization

將原始特征向量輸入至調參后的RF-RFE模型中，采用十折交叉驗證法，從當前的109個特征中修剪最不重要的特征。在修剪的集合上遞歸地重復該過程，直到最終到達所需特征的數量，在交叉驗證中得到最佳特征的數量如圖8所示，最優特征子集重要性排序如圖9所示。

由圖8可得出最佳的特征數量為22個，相比較原始特征集減少了87個特征，得到最優特征子集重要性排序如圖9所示，其中u6X15表示模態u6的特征X15。由圖9可得，所篩選出的22個特征重要性之和為0.554(所有特征重要性和為1)，說明此特征選擇的方法不僅極大程度減少了特征數量、去除了冗余特征，同時所篩選出的特征鑒別能力也較強。

4.4 分類試驗

將選擇好的最優特征數據集輸入至RF算法中進行分類識別。在分類試驗中，將最優特征數據集隨機分為5i(1≤i≤5)份，其中第i份為測試集，其余4份為訓練集，將5次結果取平均值作為最后測試結果，結果如表3～表5所示。這樣可以有效減少測試集、訓練集選取不同樣本帶來的誤差，使得結果更為真實有效。

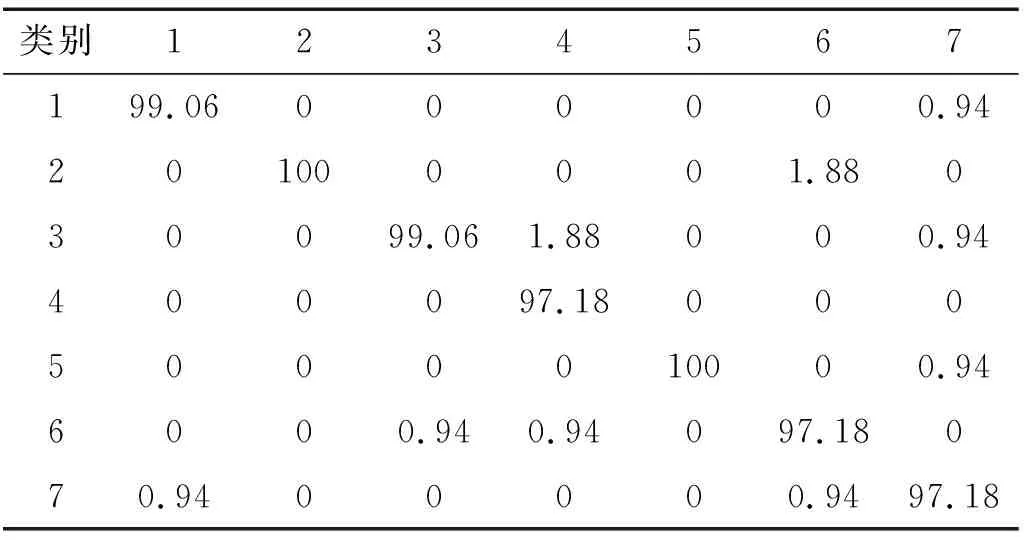
表3 隨機森林分類混淆矩陣Tab.3 Random forest classification confusion matrix

混淆矩陣[27]描繪了各測試樣本數據的真實屬性和預測結果之間的關系，可以用于評價分類算法的性能，如表3為隨機森林分類準確率的混淆矩陣，其第一行為實際類別，第一列為預測類別。由表看出異物與脫盆架的識別率達到100%，良品識別率為99.06%，同時可以計算出平均識別率為98.61%，說明該方法分類效果好，同時具有更好的特征區分度。

同時為了說明本文方法的優勢，進行了對比試驗。對7種揚聲器單元進行WPD分解；分解之后對每個子帶提取特征后進行特征選擇；最后使用RF、Adaboost及SVM進行分類試驗，分類結果如表4所示。

表4 不同分解方法及不同分類器結果對比Tab.4 Comparison of different decomposition methods and results of different classifiers

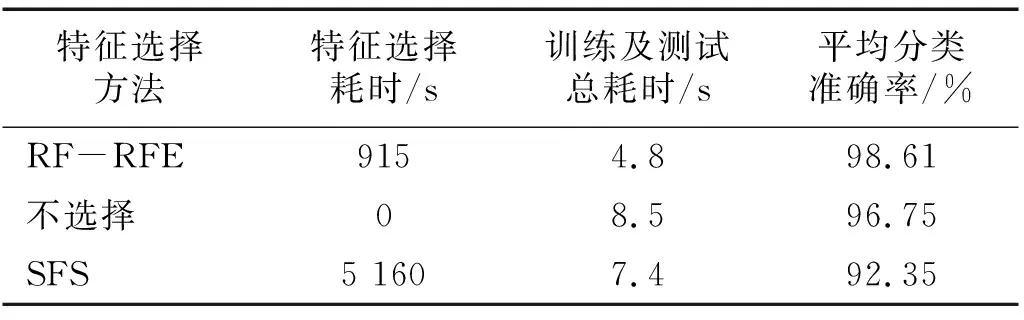
表5 特征選擇方法對比Tab.5 Comparison of feature selection methods

由3個分類器的平均分類準確率可以看出，經VMD分解后，分類效果要優于WPD，說明VMD分解算法能將非平穩的復雜信號較好地分離開，避免了能量泄露和端點效應。在分類器方面，RF分類效果要優于Adaboost和SVM，說明了RF分類效果好，抗噪能力強。

RF-RFE與序列前項選擇(sequential forward selection, SFS)在耗時和選擇效果上進行了對比，信號分解方法為VMD，分類器為RF。表5給出了不同特征選擇方法下的結果對比，其中的耗時是全部數據的總處理時間。可以看到未經過特征選擇算法由于存在冗余特征導致分類準確率降低，同時RF-RFE在特征選擇和耗時上比 SFS 更好，RF-RFE在耗時和選擇效果上取得了較好的平衡。充分表明了本文所提方法在揚聲器異常聲分類中的具有更好的效果。

5 結 論

論文提出了一種結合VMD和隨機森林特征選擇的揚聲器異常聲分類的方法，分別提取各模態的時頻域特征，并利用RF-RFE算法篩選出最優特征子集，輸入隨機森林中進行分類識別。通過對采集到的揚聲器響應信號進行分析和試驗，結論如下：

(1)針對論文中7種揚聲器單元狀態，利用VMD分解可以將揚聲器聲響應信號較好的分離為各個模態，具有更好的自適應性和能量聚焦性，其分解效果優于WPD分解。

(2)結合隨機森林特征重要性排序和遞歸特征消除算法，能更加有效的從多維特征中選擇出鑒別能力較好的特征，在特征選擇速度和分類精度上均優于SFS。

(3)提出的基于隨機森林的分類方法在平均準確率上均高于SVM和Adaboost。表明了本文所提分類方法在揚聲器異常聲分類中有著更好的分類準確度和泛化能力。

揚聲器單元故障類型繁多，本文只選擇了7種進行分類，未來還需對多種不同的故障種類進行診斷，同時還需分析何種激勵信號能更好的激發揚聲器異常聲。