高中學生數學運算能力的培養策略高中學生數學運算能力的培養策略

◎王佳榮

(青海省西寧果洛中學，青海 西寧 810000)

前 言

高中學生只有具備良好的運算能力，才能順利解答相關問題高考對學生的運算能力提出了較高的要求，運算能力也反映了學生的學習水平高中學生正處于能力培養的關鍵階段，數學教師必須重視其運算能力的培養因此，在教學的過程中，教師要根據學生的學情和心理狀態，應用創新性教學策略，全面提升學生的運算能力

一、以反思促使學生重視數學運算

教學經驗表明，反思對于提升學生運算能力而言，有著重要的作用反思心理是一種個性化心理，個性化心理又被稱為非智力心理，它是學生學習成功的根本在教學過程中，如果教師忽視對學生全方位發展的關注，那么就無法保證運算能力的培養效果，甚至會形成一個惡性循環因此，在教學中，教師應當抓住教學契機促使學生進行反思，并基于數學運算律對運算過程進行全面審查，進而使學生及時改正錯誤但這往往容易被教師所忽略因此，教師必須要在教學中著重關注學生對運算進行的反思以及對具體運算過程、細節的檢驗，尤其要檢驗數學問題中涉及的知識點和隱含條件，防止出現遺漏如題目：直線的方程為=2+3，直線,關于直線：=-對稱，求直線的斜率這道題目隱藏條件為：直線，，過同一點，因此只要再求出直線上的一點坐標，就能求出直線的方程，進而求出其斜率

除此之外，教師要對學生的邏輯思維和數形結合思維進行培養，使學生能夠在計算時書寫正確、步驟清晰，進而提升準確率并且，教師要深化學生在檢驗反思時所使用的數學思維，鍛煉其邏輯推理能力，使其達到更高層次的運算水平必要的時候，教師要鼓勵學生制作錯題集，將錯題收錄到固定本中并進行分析這樣既能幫助學生更深層次地理解知識，也能幫助學生改掉馬虎的壞習慣，從根本上提升學生的運算能力

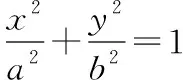
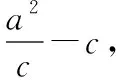
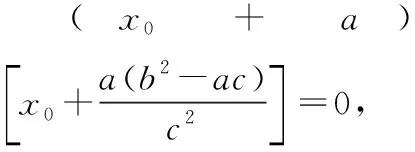
二、完善學生的認知體系，強化學生的運算能力

認知體系是學生解題的基礎，決定著學生運算能力的水平在教學中，教師應引導學生對基本數學問題進行關注，使他們積累必要的基本模型例如，在講解關于“圓上動點”的問題時，為了降低學生對題目的恐懼感，增加教學的趣味性，教師可以引入生活實例，如抻面館的師傅拉面、計算機感染了病毒、生物中的細胞分裂等，以此激發學生的學習興趣結合學生的實際情況選擇習題進行有針對性的訓練，不僅滿足了學生向深層次發展的需求，而且優化了學生的學習情緒

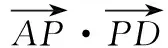
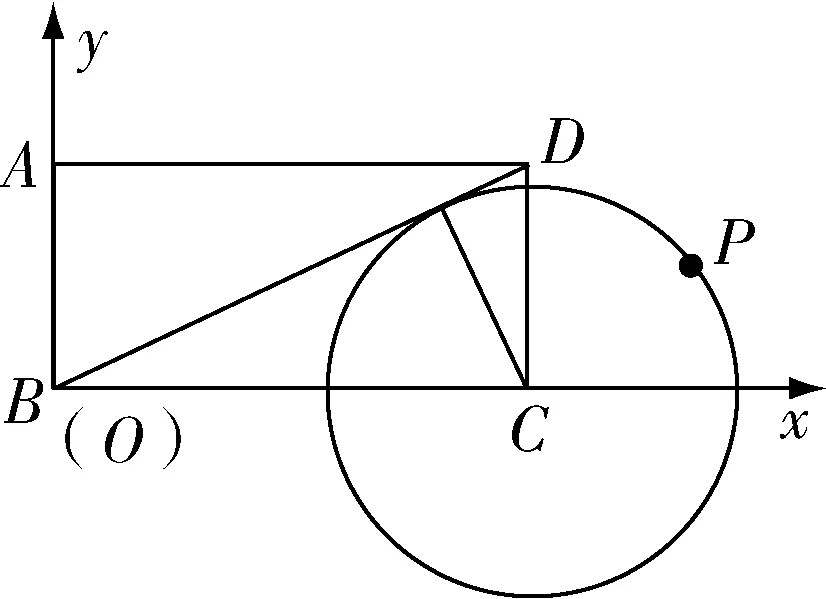
圖1

要提高學生的運算能力，除了上面的要求之外，教師還要重視學生對運算過程的理解程度例如，在應用復合函數的同增異減原理時，由于學生對這個原理了解較少，通常只是奉行“拿來主義”進行強制性記憶，因此應用效果較差為了解決這個問題，教師必須重視引導學生關注運算原理的推理過程，讓學生在感悟中強化自身的應用能力

問題：三角形中，=2，=，求此三角形的最大面積

對于本題，教師應引導學生先進行審題，找出已知條件及隱藏信息，再在理解的基礎上找出解題思路，借此構建解答幾何問題的“三步驟”：第一，構建平面直角坐標系；第二，分析動點的運動軌跡；第三，求最值對于其中涉及的運算問題，教師需要對學生掌握的知識有所了解例如，部分學生對于復合函數中“同增異減”問題涉及的算理理解不透，在解題時強行套入公式進行計算，這必然會導致運算的過程雜亂無章，不能體現運算應有的邏輯性再如，部分學生對問題的理解不完整，對運算的認知混淆，因此只對數學符號進行計算面對這些現象，教師不僅要引導學生加強對運算相關知識的理解，特別是定理與定義生成的過程，還要引導學生利用適合運算的思維方法，去確定正確的運算流程，進而提升解題的效率

三、以現代教學手段培養學生的運算思維

數學思想的引導將真實世界中的數量關系與空間關系融為一體數學思想反映了人們對數學本質的深刻認知在數學教學中，對學生數學思維的培養，實際上也是以數學基本思想為基礎的學生進入高中之后，剛剛接觸的指數函數、冪函數、對數函數等都會用到些思想對于具體的題目而言，其中經常包含隱藏條件，學生若不深入挖掘，就會給解題過程帶來很大挑戰此時，教師可以借助幾何畫板，將問題以更加直觀的方式展示給學生，并幫助學生找到其中的隱藏信息，將抽象轉化為形象，這樣可使數形結合思想的體現更加完整

問題1：鏡面可以將直射過來的光反射出去一道光線射到鏡面上后，其上有一點，坐標為(-2，3)，反射出去的光線與圓(-3)+(-2)=1相切，求反射光線的方程

此問題從字面上理解較難，但若按照條件繪制出圖形，并將所有條件都標注其中，學生理解起來思路就會更加清晰因此，教師可以先利用幾何畫板，將可能出現的情況繪制出來，然后引導學生一一分析如圖2，設射入光線為，反射光線為，根據反射光線與圓相切，可以計算出入射光線的斜率為-076或-133，反射光線的斜率為076或133，即反射光線與入射光線關于平行于軸的直線對稱，則基于不同的切點，得到兩個答案

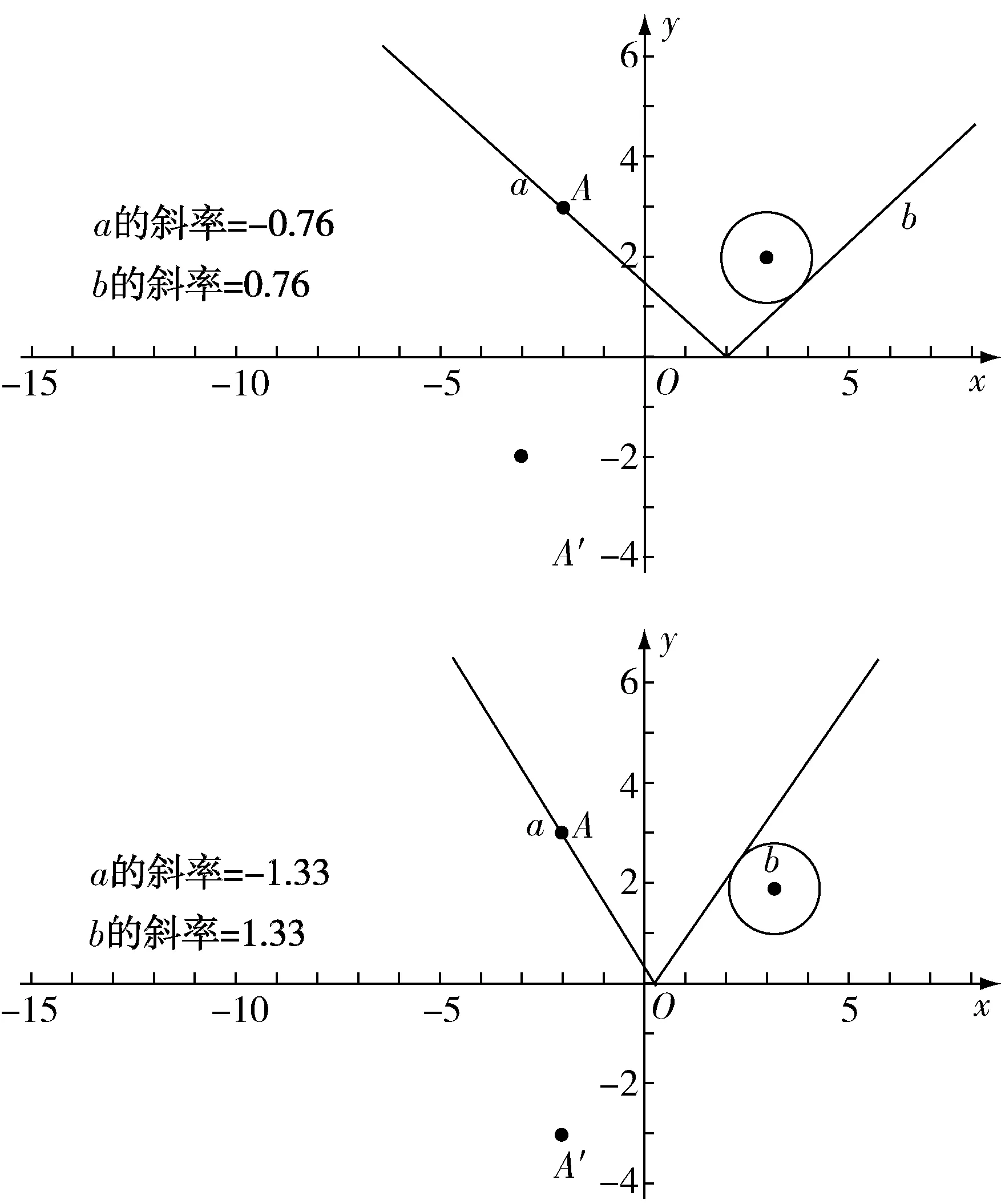
圖2

問題2：已知方程+(+4)=4，求(+1)+(+1)的最值

該問題看似簡單，但剛接觸的學生會覺得摸不著頭腦，此時幾何畫板就可以發揮作用，即將代數問題轉化為幾何圖像如圖3，題中最值的幾何意義實際上就變為點(，)到點(-1，-1)的距離，而幾何畫板本身就有度量的功能，因此可以通過測量線段的長度在實際操作中，發現只有,,三點共線的時候，才有最值這也就意味著學生觀看幾何畫板后可以自主解答

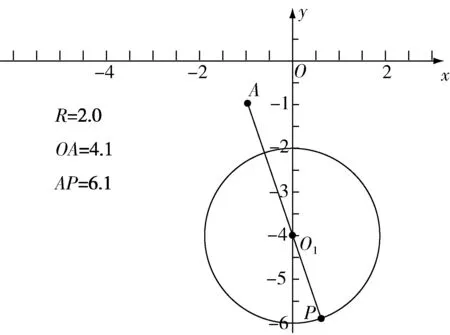
圖3

問題3：已知(0,2),(2,0),(-1，1)，若過點的直線與線段相交，求直線斜率的取值范圍

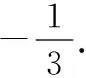
以上幾道題目是高中階段常見的幾類題型，因為其具有一定的復雜性，所以很多學生在運算過程中會感覺摸不著頭腦教師結合幾何畫板帶領學生分析，讓學生在頭腦中建立運算問題的動態表象，進而加強學生的直觀感受，強化其運算思維

四、溫故知新、培養學生運算能力

高中數學教師應重視對學生“雙基”的有效落實，要讓學生更加熟練地掌握數學概念以及法則，只有這樣，學生才能進一步理解相關計算原理，從而將這些知識全面掌握此外，高中數學教師應有意識地引導學生對一些比較容易出現錯誤的知識點進行分析，使學生通過對比去發現知識點與知識點之間的區別與聯系

在實際教學中，教師可以幫助學生鞏固舊知識，也可以引進多樣化的教學方法，讓學生在課堂中進行變式思考，對自己不會的練習題進行全面分析如此一來，學生能夠在思考的過程中鞏固之前所學習的知識，并能夠讓自身的運算能力得到有效提高

例如，很多學生在解決與通分相關的問題時，比較常見的錯誤就是學生并不了解通分，他們會將其與去分母的方法混淆對于這種情況，數學教師可以讓學生進行反思：自己究竟錯在什么地方？怎樣才能夠改正這些錯誤？學生通過對問題的思考，能更加全面地理解什么時候去分母、什么時候通分，這對于學生運算能力的提升起到了非常大的作用

五、查缺補漏，解決學生遇到的數學問題

在初中數學教學時，教師對于運算要求并不高，并且在進行解題時，也不注重方法以及技巧這種情況導致很多學生在進行轉換、恒等變形方面的運算能力不高

目前，初中教材中刪除了乘法公式中的立方差以及立方和等公式但是學生在高中階段需要在解題時靈活應用這些技巧，這就導致學生在解題過程中遇到了困難初中數學教學內容都是由淺至深、循序漸進的，但是高中階段的數學教學內容覆蓋的區域比較廣闊在這種變化下，學生的學習難度增加因此，高中數學教師應該將初中教材進行全面的了解，查缺補漏，更加全面地掌握知識以及解題的有效技巧，讓學生在學習數學知識的過程中能夠更加輕松，進而減輕學生的學習壓力，提高學生的學習效率，為學生日后的學習奠定良好的基礎

六、重視習題訓練，提高學生的運算能力

提升學生的運算能力并不是一朝一夕就能夠完成的，這是一項非常艱苦且長期的任務事實證明，只有讓學生反復練習，其運算能力才能夠得到提高對運算能力提高與否的判斷，可以以學生對計算方法能否熟練掌握，學生在計算過程中的速度以及準確性，學生在學習以及思考的過程中得出的計算技巧等為指標，如果這些方面都能得到突破，那就說明學生的運算能力得到了顯著提高

例如，在進行“數列求和”中的“錯位相減法”的教學時，教師發現很多學生在做完大量的練習題之后，能夠發現錯位的概念，進而對知識點有相對全面的了解，但其又要經歷較長時間，才能對其他一些相關知識進行整合，這樣的效率顯然偏低在這樣的背景下，高中數學教師可以適當地為學生進行拓展訓練訓練時，教師要通過題目的選擇，讓學生在練習的過程中更加有層次感，從而讓學生更加全面地掌握知識教師教授學生數學知識時所運用的技巧，也能夠對學生運算能力的提升起到積極作用值得一提的是，訓練必須要有量的保證，只有這樣，學生才能夠在解決數學問題的過程中熟能生巧，從而保證運算策略選擇與運用的合理性及準確性

例如，在教學“不等式的基本性質”的過程中，會出現運用函數思想處理不等式的問題，這類問題能夠開拓學生的思維具體來說，函數作為體現兩個變量之間關系的一種模型，其對于處理不等式問題具有很好的工具性作用在實際解題中，學生對不同形式的基本函數較為熟悉，此時若學生可以充分借助函數知識來解題，就能夠縮短解決問題時間，提高學習成績

問題：已知實數(0≤≤4)，若不等式++3>4+恒成立，求的取值范圍

在解決本題時，若圍繞自變量構建函數模型，即=+(-4)+3-，把問題轉變為在0≤≤4的情況下，>0恒成立的問題，則在具體的計算中要借助二次方程實根分布的特點進行處理，這一解題過程相對煩瑣如果引進函數思想，把不等式問題進行簡化處理，即設()=(-1)+(-4+3)，針對0≤≤4的情況，()>0恒成立，那么(0)>0與(4)>0必須同時滿足條件，進而得到的取值范圍是{|<-1或>3}

綜上所述，在高中數學教學中培養學生的運算能力是教學的重點運算能力的培養對學生的計算能力、推理能力和邏輯思維能力的要求較高，需要較長的培養時間才能夠獲得理想效果在具體的教學過程中，教師必須摒棄傳統的教學理念，從學生的角度出發，完善學生的知識體系，加強學生的反思過程，只有這樣，才能培養出運算能力強的學生