Fusionable and fissionable waves of(2+1)-dimensional shallow water wave equation

Jing Wang(王靜) Xue-Li Ding(丁學(xué)利) and Biao Li(李彪)

1Basic Teaching Department,Fuyang Institute of Technology,Fuyang 236000,China

2School of Mathematics and Statistics,Ningbo University,Ningbo 315211,China

Keywords: fissionable wave,fusionable wave,breather wave,higher-order lump

1. Introduction

The interaction solutions of nonlinear partial differential equations are a topic of general interest in nonlinear systems.[1–4]Among them, shallow water wave equation has been one of the hottest issues in recent years,[5–11]such as marine engineering,hydrodynamics,mathematical physics in other fields. Because its exact solution is a special solution existing stably in space,[12]it has very important practical significance for many complex physical phenomena[13]and some nonlinear engineering problems. So far, the phenomena of soliton fission wave and fusion wave[14]and the interaction solutions of(2+1)-dimensional shallow water wave equation(SWW)have been studied in a small amount.

The main purpose of this article is to study the fusion and fission waves and some interaction solutions of the (2+1)-dimensional SWW equation,[5]which is usually written as

this equation has been used with tsunamis,atmospheric circulation, river transport, virtual reality, and other issues widely.Many authors obtained various forms of solutions to Eq. (2)by using the Hriota bilinear method, Darboux transformation method,etc.[6–11]Equation(1)can be transformed into the following form by using the Hriota bilinear method:

Recently, some scholars have paid continuous attention to the phenonmena of fission and fusion.[14–16]Wanget al.took the Burgers equation and the Sharma–Tasso–Olver equation as two concrete examples to show the fission and fusion of the solitary wave and the soliton solutions respectively which are studied by means of the Hirota’s direct method and the B¨acklund transformation.[17]Later,from the Levi spectral problem, two basic Darboux transformations of the Sharma–Tasso–Olver equation have been obtained. Then from the trivial seed solution, the authors set the multi-kink solutions and soliton fission and fusion solutions into the following form:[18]

However, this approach is too special to get the interactions between fissionable or fusionable waves and other types of waves. In order to generate the hybrid solutions mentioned before,Chenet al.changedN-solton solutions into the following form:

whereξj,Aijhave been given in Ref.[19].Taking this method,some hybird solutions are obtained,such as an interaction between a first-order lump wave andN-fissionable waves. On the basis of Eq.(1), no matter how constrained it is, a hybrid of fissionable waves and fusionable waves cannot be obtained.The reason is that equation(1)has fewer terms than the classicN-soliton solutions.

Based on the classicN-soliton solutions, we introduce a new constraint to get a variety of hybrid solutions containing fission and waves in this paper. In order to illustrate our ideas clearly,we will consider a specific example: the(2+1)-dimensional shallow water wave equation.

2. Fissionable and fusionable waves

TheN-soliton solutions of Eq.(3)can be easily found by using bilinear method:

where

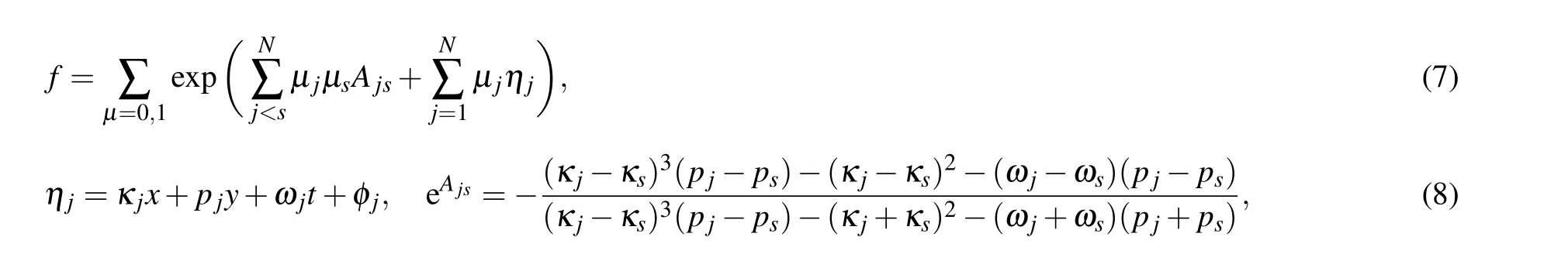
with

In order to obtain the fissionable and fusionable waves,we add the exp(x)range to remove some items in Eq.(7). The exp(x)=0 is true if and only ifx=ln(0).The exp(x+ln(0))=0exp(x)=0,if allAjs=ln(0),then equation(7)can be converted into Eq.(4). IfAjs=ln(0),3≤j ＜s ≤N,then equation (7) converts into Eq. (5). This leads to the following interesting conclusion.

Based on theN-soliton solutions,theM-fissionable waves andL-fusionable waves can be derived through the following constraints:

It is noted that theM-fissionable waves do not simply refer to the fissionable phenomenon, but rather to fissionable or fusionable phenomenon produced byMlinear waves.Mfissionable waves are described for ease of writing only.Equation (11) has two cases: one case corresponds to fissionable phenomenon and other to fusionable phenomenon.

WhenM= 1,L= 1, the one-fissionable or fusionable wave can be obtained

The form in Fig.1(a)shows one-fusionable wave,as can be seen from panels (b) and (c), the solitons gradually converge to form the fusion wave.Panel(d)shows one-fissionable wave,with the change of time from panels(e)and(f),the soliton gradually breaks up with time.

WithM= 2,L= 2, an interaction between twofissionable or fusionable waves can be described by the following expression:

The relevant parametersAjs,Psare given in Eqs.(10)and(11)respectively. With appropriate constraints, equation(17)can be described as three basic types of interaction between fissionable waves and fusionable waves: the interaction between two-fusionable waves, the hybrid of one-fissionable wave and one-fusionable wave, and the nonlinear superposition between 2-fissionable waves. The specific parameters are given as follows:

Case I

an interaction between one-fusionable wave and onefissionable wave can be got by substituting Eq. (21) into Eq.(17).

IfL=0,theN-soliton solutions can only be simplified to anN-fissionable wave. Most studies have only obtained pure fusion or fission waves. By selecting the following parameters,an interaction between fission prior and the fusion waves can be obtained:

an interaction wave between fusion first and then fission can be obtained by substituting Eq.(22)into Eq.(17).

The four pictures in Fig.2 vividly and intuitively illustrate the interaction of these four types of fusionable or fissionable phenomenon. The interaction between line waves is elastic,so it is reasonable to hold the view that the interaction waves obtained from theN-soliton solutions shown in Fig. 2 is also elastic.

Fig.1.(a)–(c)The one-fusionable wave can be obtained by substituting Eq.(15)into Eq.(13);(d)–(f)the one-fissionable wave can be obtained by substituting Eq.(15)into Eq.(13).

Fig. 2. (a) Two-fusionable waves, (b) two-fissionable, (c) an interaction between one-fusionable wave and one-fissionable wave, (d) an interaction wave between fission first and then fusion.

3. Interactions between fusionable or fissionable waves and line wave molecule or higher-order breather waves

we can obtain the interactions between one-fusionable wave and one-order breather wave.

4. Interactions between fusionable or fissionable waves and higher-order lump waves

A nonlinear superposition between anM-fusionable or fissionable waves andL-order lump waves can be derived if the following constraint is applied to theN-soliton solution:

among them, the lump wave is controlled by the parametersK2m,P2m,K2m-1,P2m-1. Through reasonable parameter constraints and long wave limit method, the interaction betweenM-fusionable or fissionable waves andL-lumps can be obtained.

In particular, ifM=1,L=1, we can derive the expression for a hybrid of one-fusionable wave and one-order lump wave:

through the method of long wave limit, the hybrid of onefusionable wave and two-order lump waves can be acquired.

5. Conclusion

Fig. 3. (a) An interaction between one-fissionable wave and a line wave molecule, (b) an interaction between one-fusionable wave and one-order breather wave.

Fig. 4. (a) An interaction between the hybrid of one-fusionable wave and one-order lump wave,(b)an interaction between the hybrid of one-fusionable wave and two-order lump waves.

In this paper, the fissionable waves, fusionable waves,breather waves,lump waves,and hybrid waves of the(2+1)-dimensional shallow water wave (SWW) equation are studied by Hirota’s bilinear method and long wave limit method.Based on theN-soliton solutions and reasonable constraint parameters, the fusionable waves, fissionable waves, and higher-order breather waves of the SWW equation have been obtained. WhenM= 1,L= 1, one-fissionable and onefusionable wave can be obtained by a series of special parameter constraints,the dynamic image is shown in Fig.1. WhenL= 2,M= 2, we can get two-fissionable, two-fusionable waves,and some mixed waves,which are exhibited by threedimensional Figs.2 and 3. The corresponding long wave limit method is used to construct high-order lump waves. At the same time, we have obtained the dynamic graphs of the hybrid of the fusionable or fissionable waves,one-order and twoorder lumps displayed by Fig. 4. In addition, the method of deriving fissionable or fusionable waves proposed in this paper can be extended to other (2+1)-dimensional integrable equations. In the near future, based on this method, we will discuss the moving path of lump in hybrid solutions, including different types of combinations in lump wave, line wave,and other types of waves.

Acknowledgments

Project supported by the Excellent Talents Project of Colleges and Universities in Anhui Province of China (Grant No. gxyqZD2020077), the School-level Scientific Research Projects(Grant No.2021KYXM08),the National Natural Science Foundation of China (Grant No. 11775121), and K. C.Wong Magna Fund in Ningbo University.