Molecule opacity study on low-lying states of CS

Rui Li(李瑞) Jiqun Sang(桑紀(jì)群) Xiaohe Lin(林曉賀) Jianjun Li(李建軍)Guiying Liang(梁桂穎) and Yong Wu(吳勇)

1Department of Physics,College of Science,Qiqihar University,Qiqihar 161006,China

2National Key Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

3Faculty of Foundation,Space Engineering University,Beijing 101416,China

4School of Data Science and Artificial Intelligence,Jilin Engineering Normal University,Changchun 130052,China

5HEDPS,Center for Applied Physics and Technology,Peking University,Beijing 100084,China

Keywords: CS,transition dipole moment,opacity,excited state

1. Introduction

The CS molecule is of great interest since it plays a key role in atmospheric and astrophysical circumstances, which draws great attention from researchers.[1–5]The molecule has been detected in the diffuse clouds, dense clouds, molecular clouds, interstellar clouds, comets, carbon-rich stars and other galaxies. In the atmospheric and astrophysical investigations, the opacity between low-lying states are used to determine species,isotopic abundances and number densities in the environment.Thereby,spectroscopic properties of CS provide worthwhile information to an extensive understanding for the intermediate processes occurred in the upper atmosphere.CS molecule and sulfur-containing molecules in the stratosphere are also related to formation of sulfate aerosols,which may lead to acid rain effect and global climate change.[6]Hence,electronic structure and transition properties of the CS molecule have been continually arising interest in the past several decades.

The large numbers of astronomical detections of CS and the key role in the Earth’s atmosphere have motivated a great deal of experimental studies. In experiment, the wavelength region of CS ranges from the microwave to ultraviolet (UV).In 1934,the pioneer work of main A1Π–X1Σ+transition was performed by Crawfordet al.[7]Later,the rotational spectrum of CS was firstly detected by Mockler and Bird.[8]The rotational spectrum of CS was also photographed by Lovas and Krupenie, and dipole moments and rotational constants were fitted by experimental results.[9]The experimental spectrum in the millimeter region was observed by Bogeyet al.,[10,11]and the spectroscopic constants of the X1Σ+state were obtained.More recently, the investigation in the wide wavelength region was extensively studied by Kimet al.[12]and Gottliebet al.,[13]and the accurate frequencies of rotational transitions were provided in their studies.

The first work in the infra-red wavelengths was carried out by Todd,[14]who detected theν=2–0 vibration–rotation band of the X1Σ+state of CS.Subsequently,the investigation of the infra-red region was extended by Winkelet al.[15]and Burkholderet al.,[16]and high resolution of theν=1–0 absorption band and theν=1–0“hot”band for the X1Σ+state were measured. On the basis of vibration–rotation and pure rotation spectrum in preceding experimental data, Conxon and Hajigeorgiou determined accurate spectroscopic potential energy curve (PEC). Then, the spectroscopic constant of the X1Σ+state was improved by Ramet al.,[17]who determined the spectroscopic constant from Δν=1 vibration–rotation bands up toν= 9–8. Recently, Ueharaet al.[2]measured Δν= 1 transitions of the X1Σ+state withν ≤7 to a better precision than Ramet al.Pauloseet al.[1]used the spectroscopically-determined PEC and dipole moment to present vibration–rotation line lists.

A series of UV band (A1Π–X1Σ+, A′1Σ+–X1Σ+, a3Π–X1Σ+, and so on) were extensively studied by different research groups. Bergeman and Cossart[18,19]observed a number of spin-allowed (A1Π–X1Σ+) and spin-forbidden (a3Π–X1Σ+,d3Δ–X1Σ+,and e3Σ-–X1Σ+)transition bands,and the interaction between those low-lying excited states were discussed in detail. The A1Π–X1Σ+band system was recorded by Mahonet al.,[20]and electronic transition moment of the A1Π–X1Σ+transition were estimated by the corresponding experimental result. The emission spectrum of A′1Σ+–X1Σ+was photographed by Dornh¨oferet al.[21]employing timeresolved fluorescence technique,and the transition property of A′1Σ+–X1Σ+was analyzed.

On the theoretical side, the electronic structure and transition properties of CS have been investigated by different theoretical method. Robbe and Schamps[22]used SCF-CI approach to calculated electronic structure, wavefunction and dipole moment of valence state of CS.Later,the PEC of X1Σ+state were determined by Wilson[23]by using diagrammatic many-body perturbation theory. Ornellas[24]determined accurate PECs of X1Σ+and A1Π states by utilizing MRCI method,and the transition dipole moment of the A1Π–X1Σ+transition were evaluated. The structures for triplet states (a3Π, d3Δ,a′3Σ+and e3Σ-)were studied by Hochlaf using CASSCF and MRCI method.[25]

As discussed above, the CS molecule has been studied widely by different research group. However, the existing computations of CS molecule are dominantly concentrated on structures of several electronic states.Regarding the large state density and interaction of low-lying states,the accurate calculations of electronic structure and spectroscopic properties of CS still remain sparse. As far as we know,the only spectrum simulation is the vibration–rotation line lists computations of the X1Σ+state of CS by Pauloseet al.[1]In this work,we carry out high-level MRCI study on the low-lying states of CS.The PECs,dipole moments and transition dipole moments are evaluated at the MRCI level of theory,and then vibration–rotation line between low-lying states are calculated at different temperature conditions.

2. Theoretical method

In the present work,the MOLPRO package[26]is used to calculate the PECs of singlet and triplet states correlated with the lowest dissociation limit of CS molecule. All the calculations are done in theC2vgroup, which is subgroup ofC∞vpoint group for CS molecule. The corresponding relationship for the irreducible representations ofC2vandC∞vgroup are Σ+to A1,Σ-to A2,Π to B1+B2and Δ to A1+A2. For the C and S atoms,the contracted augmented correlation-consistent polarized quintuple zeta aug-cc-pwCV5Z-DK basis sets[27–29]is adopted. Within the internuclear distance range of 0.975–6.0 ?A,the molecular orbitals of the X1Σ+state are computed by the Hartree–Fock approach. In order to balance molecular orbitals applied in the subsequent calculations of electronic correlation, we utilize the state-averaged complete active space self-consistent field (SA-CASSCF)[30,31]approach to optimize the preceding Hartree–Fock molecular orbitals. In the SA-CASSCF calculations, all the 12 singlet and triplet Λ–S states, which are two1Σ+, one1Σ-, two1Π, one1Δ,two3Σ+, one3Σ-, two3Π and one3Δ, are taken into account simultaneously. The active space in the SA-CASSCF calculations is constructed by 8 molecular orbitals, which associates with C 2s2p and S 3s3p atomic orbitals. In theC2vgroup, the active space is denoted as (4,2,2,0), in which ten electrons are spread across 8 molecular orbitals. Subsequently, by employing the calculated CASSCF energies as reference values, the energies of the 12Λ–S states are determined by internally contracted multireference configuration interaction method[32,33](MRCI+Q) (including Davison size-extensivity correction).[34]The scalar relativistic effect is taken into account through third-order Douglas–Kroll and Hess integrals.[35,36]The PECs are presented by linking the energy points of Λ–S states via taking into account the noncrossing rule.

Under the Born–Oppenheimer approximation condition,the electronic Schr¨odinger equation of diatomic molecules can be written as

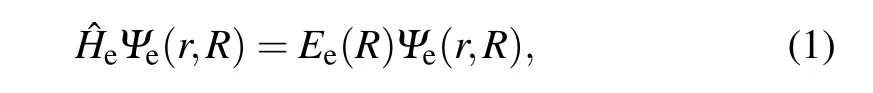
in which ?Heis Hamiltonian of theNelectrons of diatomic molecules,Ψe(r,R) andEe(R) are the eigen-function and eigen-energy,respectively.

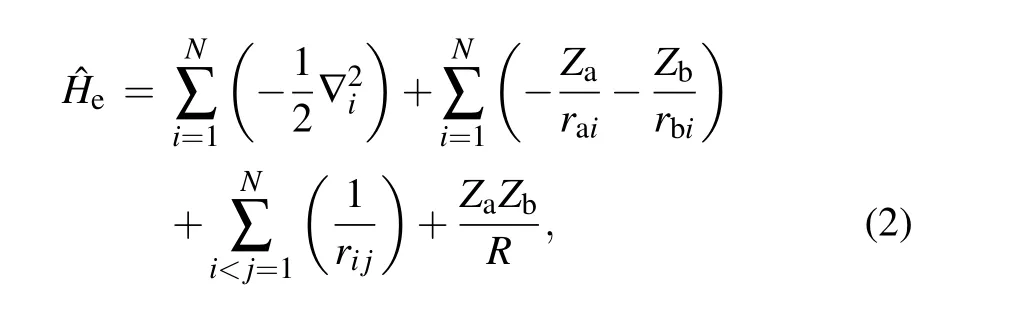
whereZaandZbare the charge number of nucleus A and B.

On the basis of calculated energies of electronic states,the eigenvalues and wave functions of vibration–rotation states can be obtained by solution of radical nuclear Schr¨odinger equation

whereν′andJ′are vibrational and rotational quantum numbers,αis fine-structure constant,ωυ′j′,υ′′j′′is transition frequency between different vibration–rotation levels,SJ′J′′is the line strength,D(R)is the transition dipole moment,andφJ(rèn)′,J′′is H¨onl–London factor. The H¨onl–London factorφJ(rèn)′J′′is defined as

The expressions of formulas(1–6)can be found in Ref.[36].

Molecular opacity is computed with integrated line strengths,[37]which is given by

in which Einstein’s coefficientsAis obtained from Eq. (4),ΔE′′is the energy gap of the correlated two states,his the Plank constant,cis the speed of light in vacuum,kis the Boltzmann constant,EV′J′,00is the excitation energy of the lower state in cm-1,and the total internal partition functionQ(T)is defined by summing up concerned electronic state weighed by the Boltzmann factor utilizing

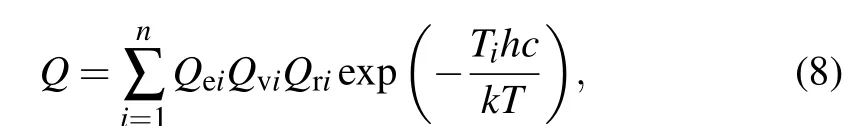
whereTis temperature in environment andTiis the excitation energy of electronic stateiand become zero for the ground state(i=1).

3. Result and discussion

3.1. Potential energy curves, spectroscopic constants and vibrational levels

The 12Λ–S states associated with the lowest dissociation limit(C(3P)+S(3P))of CS are evaluated at aug-cc-pwCV5ZDK/MRCI+Qlevel of theory. The PECs of the 12Λ–S states are presented in Fig.1. For the sake of visual clarity,we display the singlet Λ–S states and triplet Λ–S states in panels(a)and (b), respectively. And then, we use numerical method to calculate nuclear Schr¨odinger equations to determine spectroscopic constants. For the convenience of comparison, our calculated spectroscopic constants,including transition energyTe,vibrational frequencies(ωeandωexe),equilibrium distanceReand dissociation energyDe,are listed in Table 1,along with the data of previous experimental and theoretical investigations. The spectroscopic constants of electronic states can be served as an effective method to check the precision of electronic structure computation.

As displayed in Fig.1,the Λ–S states 21Π,23Π and 33Σ+are qusibound states,and the A′1Σ+state has shallow potential well with a depth of 0.33 eV.The other 8 Λ–S states are typical bound states, which have potential well deeper than 2.40 eV.In Table 1, one can clearly see that our calculated spectroscopic constants of bound states are generally in good agreement with existing experimental results, as well as the previously available theoretical data. For the X1Σ+state, theωe,ωexe,BeandReare computed to be 1284.2 cm-1,6.35 cm-1,0.8179 cm-1and 1.5369 ?A, which differ from the latest experimental data by only 1 cm-1, 0.152 cm-1, 0.0021 cm-1and 0.0019 ?A.Our calculated dissociation energy of the X1Σ+state is 7.42 eV,which is only 0.01 eV smaller than experimental value of 7.43 eV.[36]Our calculated spectroscopic constant of the X1Σ+state has higher accuracy compared with the previously available theoretical results.[24,25]For the first excited state a3Π, our calculations present a deep well depthDeof 3.92 eV located at theReof 1.5724 ?A. The calculated value ofRe(1.5724 ?A) is more close to the experimental value of 1.5691 ?A, as compared with previous theoretical data. Our calculatedTeof a3Π (28328 cm-1) agrees well with existing theoretical work of 28173 cm-1,and our calculatedTeof a3Π differs by 1298 cm-1(5%) from previously available experimental data.[18]

Fig.1. MRCI+Q potential energy curves for singlet and triplet states of CS along with internuclear distance R.

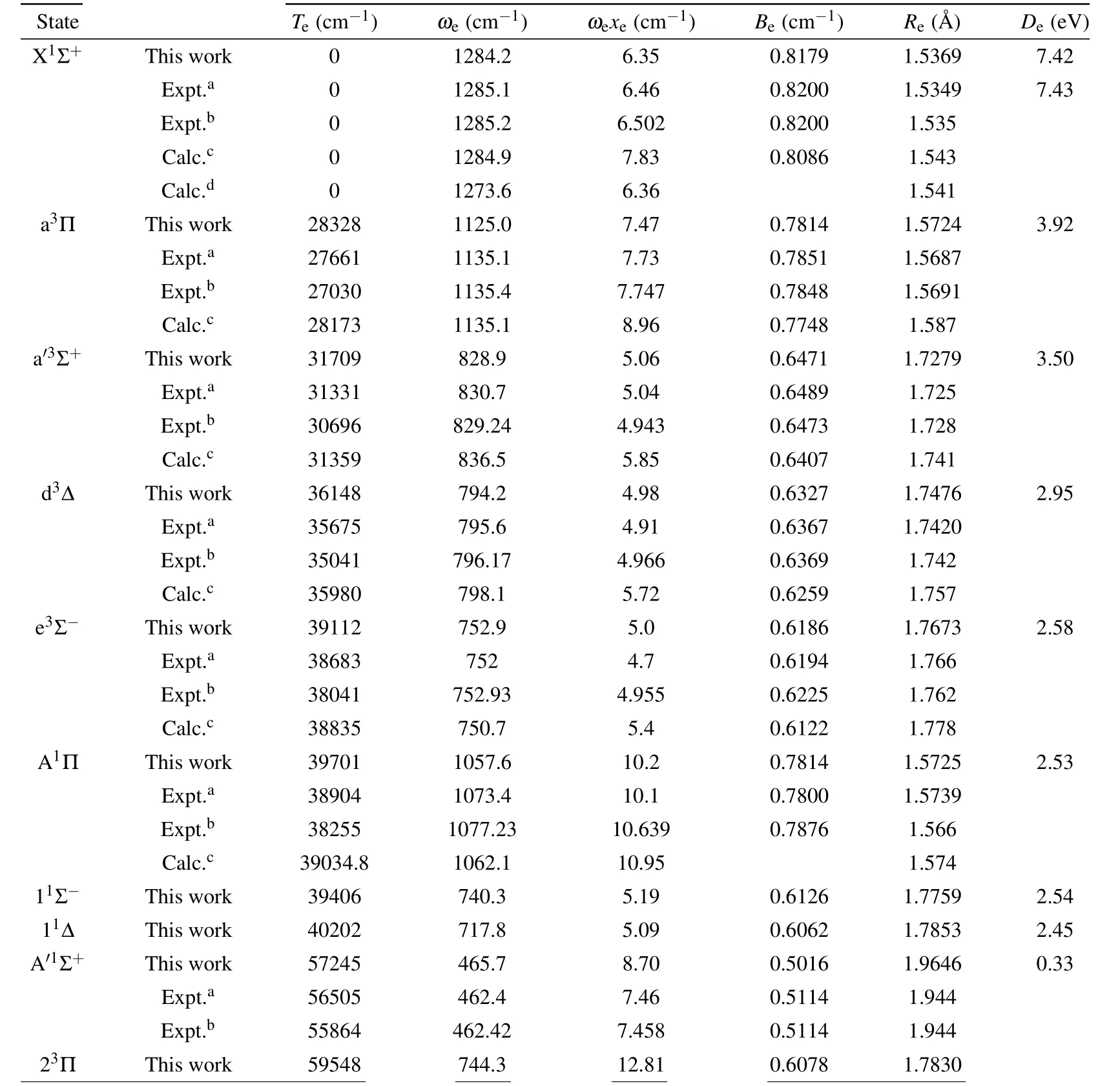
Table 1. Spectroscopic constants of bound Λ–S states of CS.

In addition,the previous experimental results in Refs.[18,36] exhibit a relative large difference (～600 cm-1), which may be caused by the experimental error originated from the perturbation of the nearby excited states (d3Δ, a′3Σ+and e3Σ-). Similar situations are found in excited states located at the excited energy range of 28000–40000 cm-1,which can also be explained by perturbation caused by a very high density of the excited states. Hence,more accurate spectral studies should be carried out to investigate the perturbations of the excited states. For the first singlet excited state A1Π,the dissociation energyDeis estimated to be 2.53 eV,which can hold 26 vibrational levels. Theωe,ωexeandBeare computed to be 1057.6 cm-1,10.2 cm-1and 0.7814 cm-1,which are in good accordance with the latest experimental data of 1077.23 cm-1,10.639 cm-1, and 0.7876 cm-1. TheReis evaluated to be 1.5725 ?A,which is more close to the latest experimental value of 1.566 ?A.[18]Our calculatedTediffer by less than 800 cm-1(2%)from the latest measurements.[18]For the second singlet excited state A′1Σ+,the well depth is computed to be 0.33 eV,which can only support 5 vibrational states. Good agreements are achieved for theωe,BeandRe. In our work, the calculated spectroscopic constants of A′1Σ+areωe=465.7 cm-1,Be=0.5016 cm-1andRe=1.9646 ?A, and the ones determined by Ref.[18]areωe=462.42 cm-1,Be=0.5114 cm-1andRe=1.944 ?A.Our MRCI+QcalculatedTeis 57245 cm-1,which differs by 1381 cm-1(2%) from most recent experimental value of 55864 cm-1.[18]Theωexeis calculated to be 8.70 cm-1,which is 1.242 cm-1larger than the experimental result of 7.458 cm-1.

In the process of determining spectroscopic constants,the vibrational levels of the ground state and exited states are also obtained. In Tables 2 and 3, the vibrational energy gap between Δν=1 are presented for X1Σ+and A1Π/A′1Σ+states along with previously available theoretical and experimental data. For the the X1Σ+state, our calculated vibration levels gap forν ≤20 agree very well with the most recent experimental data,[2]the absolute differences are less than 2 cm-1(0.2%). In comparison with existing theoretical data,[38]our calculated accuracy of vibrational levels has obviously improvement,especially for theν ≥2 vibrational levels. For the A1Π state,the vibration levels gap forν ≤4 are computed to be 1037.6 cm-1, 1016.4 cm-1, 995.9 cm-1and 975.6 cm-1,which is only about～15 cm-1(2%) smaller than the latest experimental results.[20]In addition, our calculated vibration levels gap of A1Π state are closer to experimental data.

Table 2. The vibrational energy gap(Eν-Eν-1)(in cm-1)for the X1Σ+ state of CS.

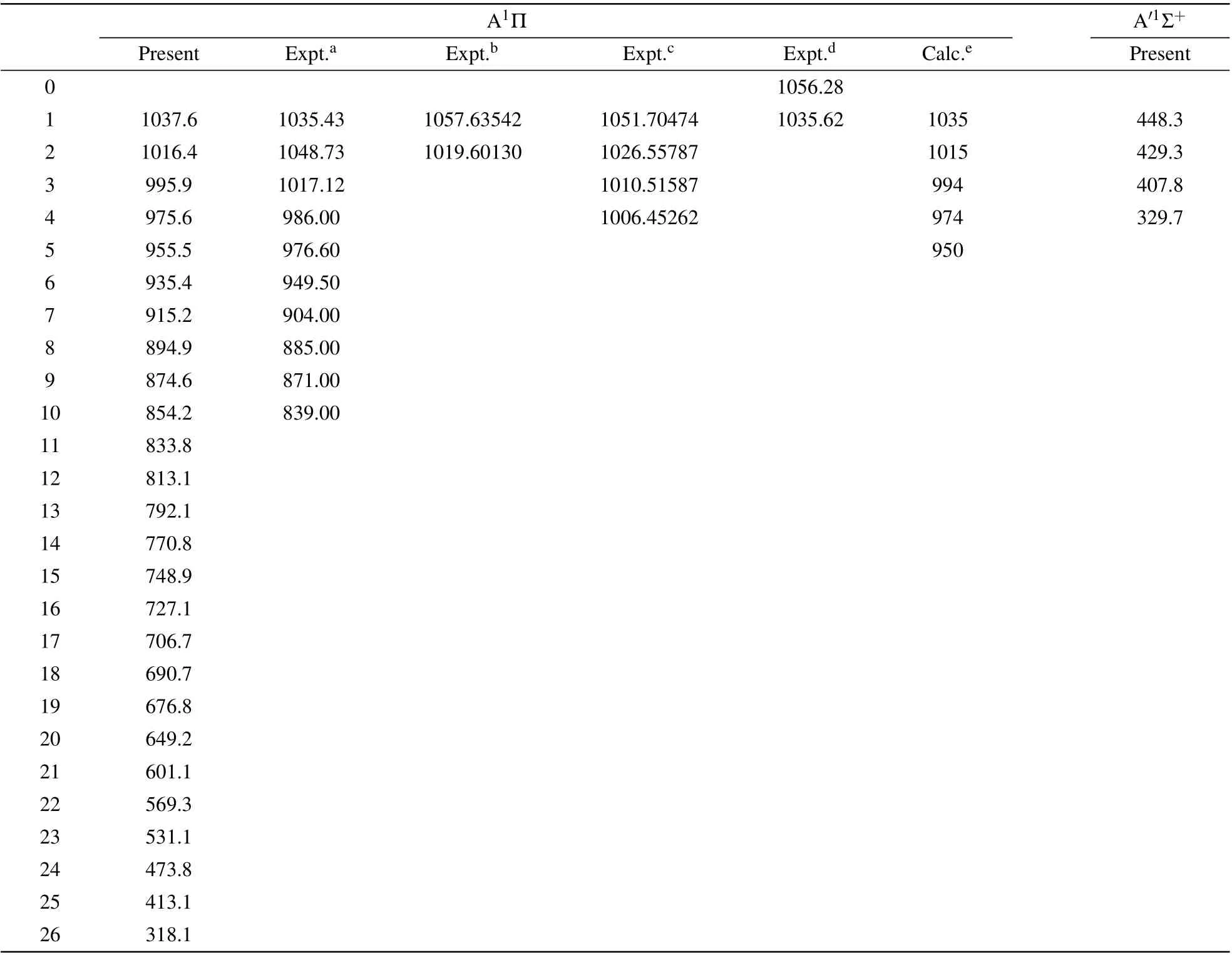
Table 3. The vibrational energy gap(Eν-Eν-1)(in cm-1)for the A1Π state of CS.

4. Dipole moments and transition dipole moments

The dipole moments and transition dipole moments of low-lying Λ–S states are computed by employing MRCI wave functions. The dipole moments curves for the singlet Λ–S states and triplet Λ–S states are presented in Figs. 2(a) and 2(b), respectively. As is well known, the vibration of dipole moment reflects the change of electronic configuration for Λ–S state. As displayed in Fig. 2, the extent of variation of dipole moments for A′1Σ+,21Π,33Σ+and 23Π are obviously large than that of other 8 Λ–S states. This phenomenon could be explained by the sharp vibration of electronic configuration of A′1Σ+, 21Π, 33Σ+and 23Π. As shown in Fig. 1, the A′1Σ+,21Π,33Σ+and 23Π are located at high excitation energy range of≥5700 cm-1, which form crossing point with high excited states. The crossing point of A′1Σ+, 21Π, 33Σ+and 23Π cause the sharp change for electronic configurations of those states, hence, the dipole moment curves of A′1Σ+,21Π, 33Σ+and 23Π change dramatically as compared with that of the other 8 Λ–S states. At the equilibrium distance(Re=1.5369 ?A)of the X1Σ+,the dipole moment is computed to be 0.77 a.u., which agree very well with available experimental data of 0.7704 a.u.[42]Both theoretical and experimental studied indicate the Cδ-Sδ+polarity of the CS molecule.At the equilibrium distanceRe=1.5725 ?A,the dipole moment of A1Π is estimated to be 0.29 a.u. As shown in Fig. 2, the dipole moments of all the Λ–S states approach to zero at large internuclear distance, indicating the dissociation products are neutral C and S atoms.

The transition dipole moments (TDMs) of spin-allowed singlet-singlet transition are given in Fig.3. For convenient of comparing, the previous TDM of A1Π–X1Σ+[24]determined by cc-PVQZ/MRSDCI level of theory are also displayed. As can be seen in Fig.3,the position of peak of TDM for A1Π–X1Σ+transition in our work and Ref.[24]are well consistent,which are both located atR=1.39 ?A.The peak value of TDM of A1Π–X1Σ+transition is 0.304 a.u., which is 0.028 a.u.larger than that in Ref.[24]. The maximum value(0.599 a.u.)of TDM of A′1Σ+–X1Σ+is located at 1.80 ?A.

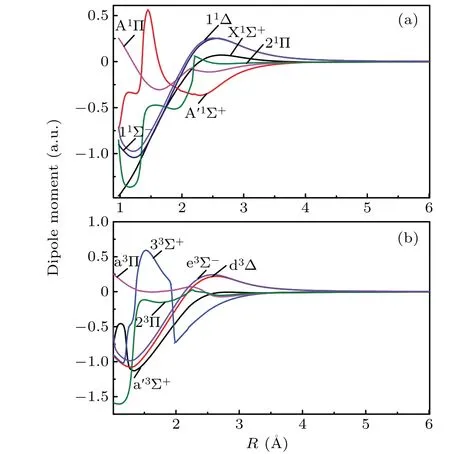
Fig.2. Dipole moment curves for singlet and triplet states of CS.

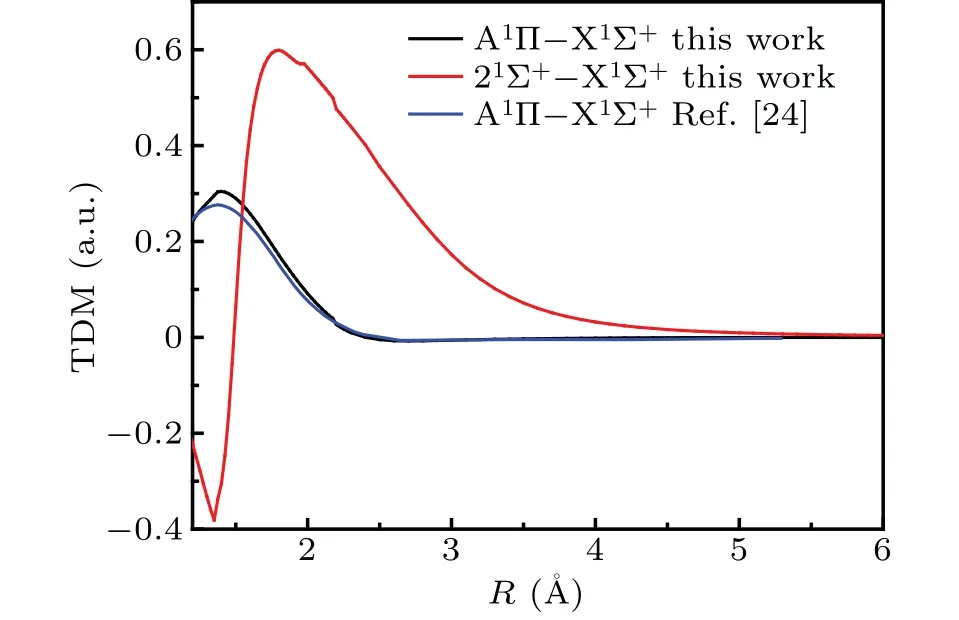
Fig.3. Transition dipole moment curves of spin-allowed transition of CS.

4.1. Opacity

Fig.4. The total internal partition functions of CS along with the temperature T (in Kelvin).

With the information of partition functions and vibration–rotation states,the molecular opacities for the X1Σ+,A1Π and A′1Σ+states are obtained from formula (7) at pressure of 100 atms for different temperatures. With the increasing of temperature and growing of density,the dissociation probability of molecule will be raised. However, the dissociation energy of X1Σ+(7.42 eV)is very large,so the dissociation probability of CS caused by thermal motion inT=4500 K is very small. In addition, the previous investigations also indicate that opacity and absorption spectrum in astrophysical field are mainly originated from molecule.[1,2]The calculated molecular opacities of X1Σ+, A1Π and A′1Σ+states of CS for the temperatures of 300 K,1000 K,1800 K,and 4500 K are displayed in Figs.5(a)–5(d),respectively. As presented in Fig.5,the spectra lie in a wide area of wavelengths,which range from UV to far-infrared. In the simulation of spectra, the spectral line is profiled utilizing a Lorentzian function with a width contributed from impact-broadening. As can be observed in Fig.5(a),there are three electronic bands attributed from three singlet states considered in this work, which associate with A′1Σ+–X1Σ+, A1Π–X1Σ+and X1Σ+–X1Σ+transitions from left to right,respectively.At low temperature of 300 K/1000 K and a pressure of 100 atms(see Figs.5(a)and 5(b)),different band systems are distinctly divided from each other. The band systems contributed from A′1Σ+–X1Σ+and A1Π–X1Σ+transitions appear at nearby 180 nm and 250 nm,which are located in wavelength range of short-wave UV.As for band system of X1Σ+–X1Σ+,there are two typical bands(fundamental vibrational transition and pure rotation transition), and the fundamental vibrational bands of Δν=1, 2 and 3 appear around 6.6 μm, 3.4 μm and 2.3 μm, while the pure rotation band of Δν=0 locates in wavelength of≥40 μm. It can be seen that the molecular opacities are very small in the 300–1500 nm wavelength range, which form a window area in the visible light(VIS)and near infrared(NIR)region. When the temperature increase(see Figs.5(c)and 5(d)),the cross section in the

Fig.5. Opacity of CS generated by vibration–rotation transitions for a pressure of 100 atm and temperatures of T =300 K,1000 K,1800 K,and 4500 K.

VIS and NIR window area is growing gradually,and the separation between different fundamental vibrational bands and different electronic bands become blurred, which are originated from the raised population on vibrational excited states and electronic excited state at high temperature. On the other hand, the cross section contributed from pure rotational transition decrease evidently because of the reduced populations on the X1Σ+, while the cross section originated from highly vibrational excited states are enhanced significantly.

5. Conclusions

In this work, accurate PECs of singlet and triplet states correlated with the lowest dissociation limit of CS molecule are computed with high-precision MRCI+Qlevel of theory.Based on calculated PECs, the spectroscopic constants and vibrational levels are evaluated by using accurate numerical method, which agree with the previous measurement. The opacities for the lowest three singlet states of CS are evaluated at a pressure of 100 atms for the temperatures of 300 K,1000 K,1800 K,and 4500 K.At the low temperatures of 300 K and 1000 K, the spectra contributed from electronic transitions (A′1Σ+–X1Σ+and A1Π–X1Σ+) are separated into distinct bands,and different vibrational bands caused by Δν=0,1, 2 and 3 of X1Σ+–X1Σ+transition are also found. With the increasing of the temperature, the populations on excited states are increased,which cause the superposition of different band transitions. Hence,the band boundaries of cross sections become blurred. This work provides accurate electronic structure and molecular opacity of CS.The present study will shed more light on the calculations of the high-precision molecular structures and opacity.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.11934004 and 12203106),Fundamental Research Funds in Heilongjiang Province Universities,China (Grant No. 145109127), and the Scientific Research Plan Projects of Heilongjiang Education Department, China(Grant Nos.WNCGQJKF202103 and DWCGQKF202104).