一種CPP- RPP- PRR 解耦并聯(lián)機(jī)構(gòu)的位置反解分析

戰(zhàn)麗娜,趙 楠*,肖淑斌

（湖南水利水電職業(yè)技術(shù)學(xué)院,湖南 長(zhǎng)沙 410131）

機(jī)構(gòu)的位置分析指的是求解機(jī)構(gòu)的輸入與輸出構(gòu)件之間的位置關(guān)系的過程。當(dāng)已知機(jī)構(gòu)輸入件的位置和姿態(tài),求解機(jī)構(gòu)輸出件的位置和姿態(tài)時(shí)稱為機(jī)構(gòu)位置分析的正解；當(dāng)已知機(jī)構(gòu)輸出件的位置和姿態(tài),求解機(jī)構(gòu)輸入件的位置和姿態(tài)時(shí)稱為機(jī)構(gòu)位置分析的反解[1-7]。本研究運(yùn)用螺旋理論[7],對(duì)CPP-RPP-PRR解耦并聯(lián)機(jī)構(gòu)的位置反解進(jìn)行了分析。

1 CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)結(jié)構(gòu)概述

CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)主要由動(dòng)平臺(tái)、靜平臺(tái)和分別固連在兩平臺(tái)之間的三個(gè)分支組成。分支一包括一個(gè)圓柱副C1和兩個(gè)移動(dòng)方向相互垂直的移動(dòng)副P1、P2,其中圓柱副C1在靜平臺(tái)上,其移動(dòng)方向是靜平臺(tái)的豎直方向,且與移動(dòng)副P1的移動(dòng)方向相互垂直；分支二包括一個(gè)轉(zhuǎn)動(dòng)副R1和兩個(gè)移動(dòng)方向相互垂直的移動(dòng)副P3、P4,其中轉(zhuǎn)動(dòng)副R1在靜平臺(tái)上,其回轉(zhuǎn)軸線是靜平臺(tái)的豎直方向,且與移動(dòng)副P3的移動(dòng)方向相互垂直；分支三包括一個(gè)移動(dòng)副P5和兩個(gè)回轉(zhuǎn)軸線相互平行的轉(zhuǎn)動(dòng)副R2、R3,其中移動(dòng)副P5在靜平臺(tái)上,其移動(dòng)方向是靜平臺(tái)的水平方向,且分別與轉(zhuǎn)動(dòng)副R2的回轉(zhuǎn)軸線和轉(zhuǎn)動(dòng)副R3的回轉(zhuǎn)軸線相互垂直。因此,從總體上看,圓柱副C1的回轉(zhuǎn)軸線與轉(zhuǎn)動(dòng)副R1的回轉(zhuǎn)軸線、轉(zhuǎn)動(dòng)副R2的回轉(zhuǎn)軸線和轉(zhuǎn)動(dòng)副R3的回轉(zhuǎn)軸線均兩兩相互平行,且都與移動(dòng)副P5的移動(dòng)方向相互垂直,其結(jié)構(gòu)簡(jiǎn)圖見圖1。

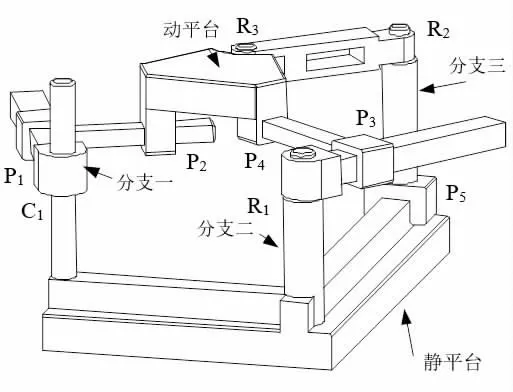
圖1 CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)結(jié)構(gòu)簡(jiǎn)圖

2 螺旋理論

對(duì)CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)進(jìn)行位置反解分析,須以螺旋理論為基礎(chǔ)。螺旋又稱旋量,線矢量是旋量的特殊形式,可以表示空間矢量的方向和位置,每個(gè)螺旋都含有6 個(gè)標(biāo)量。若把空間的兩點(diǎn)A 和B 用有向直線連接,就能決定這條空間直線AB 的方向和位置。在直角坐標(biāo)系中這條有向直線AB 的矢量可用S 表示,則直線AB 的方向可由其方向余弦確定,直線AB 的位置可通過直線上任意一點(diǎn)的矢量確定。因此,用螺旋來表示直線AB 就為=（S；S0）,其中,S0=r×S,S·S0=0。若S·S0≠0,則表示的就為旋量[7]。

在并聯(lián)機(jī)構(gòu)中,剛體的轉(zhuǎn)動(dòng)副可以用剛體的角速度的大小與一個(gè)表示旋轉(zhuǎn)軸作用線的單位線矢之積來表示,由于線矢之積與標(biāo)量表示同一線矢,故轉(zhuǎn)動(dòng)副可用螺旋表示為：

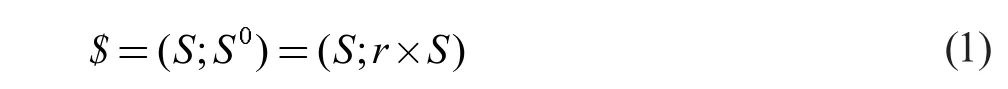
剛體的移動(dòng)副也可看成是一個(gè)瞬時(shí)轉(zhuǎn)動(dòng),轉(zhuǎn)動(dòng)軸線與S 正交,且位于距S 無窮遠(yuǎn)的平面內(nèi),則移動(dòng)副可用螺旋表示為：

其中,0 是一個(gè)1×3 的零矢量。

而圓柱副(C)則可看作共軸的一個(gè)轉(zhuǎn)動(dòng)副和一個(gè)移動(dòng)副的組合。

3 CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)位置反解分析

CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)求解位置反解,即當(dāng)給定機(jī)構(gòu)的尺寸參數(shù),已知?jiǎng)悠脚_(tái)的未知參數(shù)（x,y,）及姿態(tài)角c,求三個(gè)驅(qū)動(dòng)的輸入：分支一的轉(zhuǎn)動(dòng)角度a、分支二的移動(dòng)e、分支三的轉(zhuǎn)動(dòng)角度b。

由于該機(jī)構(gòu)只能完成動(dòng)平臺(tái)在XY 平面的移動(dòng)和繞Z 軸的轉(zhuǎn)動(dòng),所以只需考慮XY 平面的運(yùn)動(dòng)即可求解位置反解。

在XY 平面內(nèi),如圖2 機(jī)構(gòu)平面簡(jiǎn)圖所示,設(shè)靜平臺(tái)的桿長(zhǎng)分別為L(zhǎng)、g,分支一的桿長(zhǎng)分別為l、d,分支二的桿長(zhǎng)分別為e、f,分支三的桿長(zhǎng)為H,動(dòng)平臺(tái)正多邊形的內(nèi)切圓半徑為R,分支一與靜平臺(tái)之間的夾角為u,分支一與分支二之間的夾角為v,分支三與靜平臺(tái)之間的夾角為w,分支二與動(dòng)平臺(tái)之間的夾角為z,則L、H、R 三個(gè)桿長(zhǎng)為定值,u、v、w、z 四個(gè)夾角也為定值,都不會(huì)隨著機(jī)構(gòu)的運(yùn)動(dòng)而改變,但是d、f、g、l 的長(zhǎng)度會(huì)隨著輸入的改變而變化。設(shè)基坐標(biāo)建立在分支三的圓柱面圓心A 點(diǎn),動(dòng)坐標(biāo)建立在動(dòng)平臺(tái)中心,其余各個(gè)坐標(biāo)建立見圖3。

圖2 CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)平面簡(jiǎn)圖

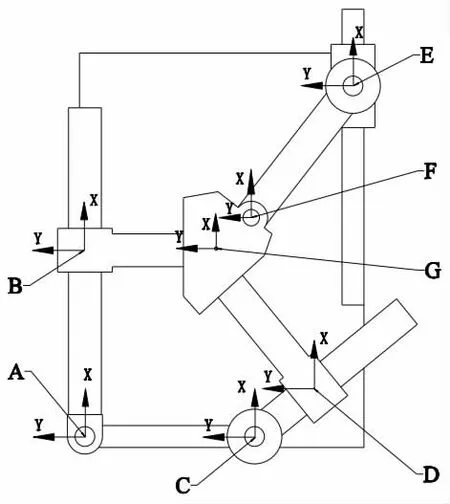
圖3 CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)坐標(biāo)系示意圖

由圖3 可知,動(dòng)坐標(biāo)位姿可以通過三條路線給定,路線一為A-B-G；路線二為A-C-D-G；路線三為A-E-F-G[6]。

根據(jù)螺旋理論,對(duì)路線一進(jìn)行計(jì)算,得矩陣如下

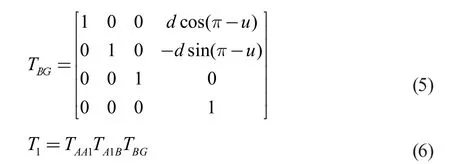
對(duì)T1進(jìn)行化簡(jiǎn),得

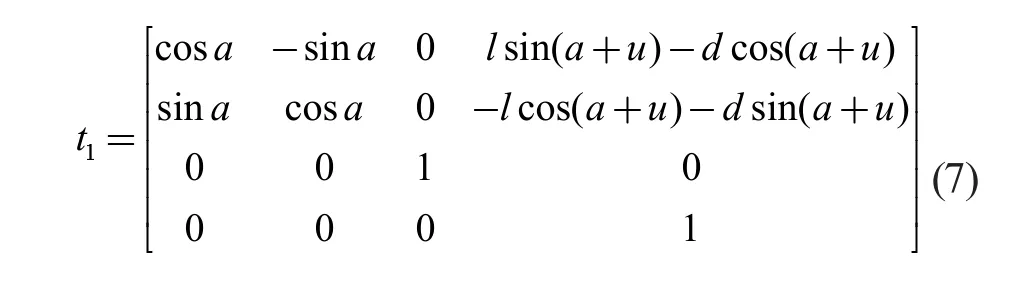
根據(jù)螺旋理論,對(duì)路線二進(jìn)行計(jì)算,得矩陣如下

對(duì)T2進(jìn)行化簡(jiǎn),得

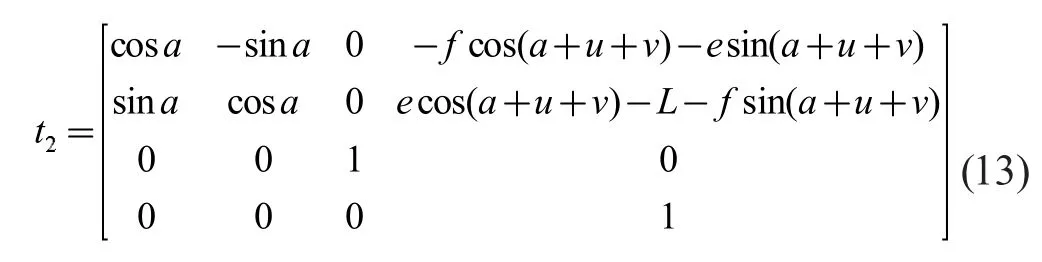
根據(jù)螺旋理論,對(duì)路線三進(jìn)行計(jì)算,得矩陣如下

對(duì)T3進(jìn)行化簡(jiǎn),得

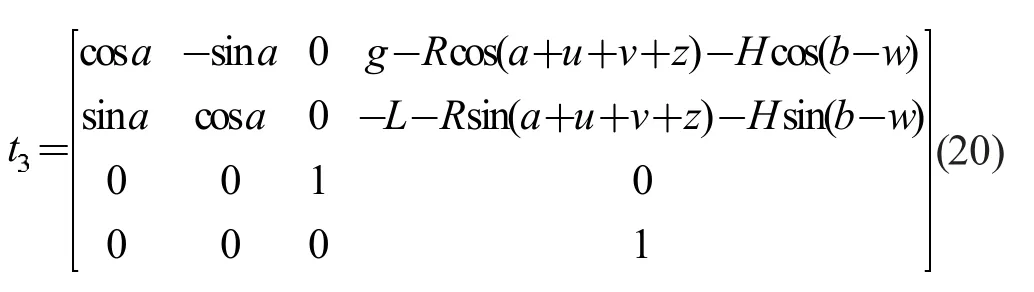
由結(jié)果可知,分支一的輸入角度a 就是動(dòng)平臺(tái)的轉(zhuǎn)動(dòng)角度c 的值。再將式(7)、(13)、(20)三個(gè)矩陣的第四列分別相等,可列出六個(gè)方程如下

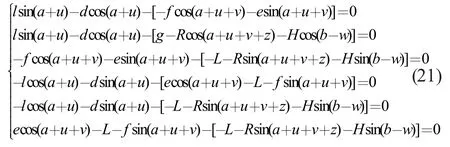
解出各分支的桿長(zhǎng)l、d、e、f、g 和分支三的輸入角度b 如下

4 驗(yàn)證CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)位置反解的正確性

CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)處于特殊位置,將其分別代入式(3)、(4)、(5)、(6)、(8)、(9)、(10)、(11)、(12)、(14)、(15)、(16)、(17)、(18)和(19)中,得

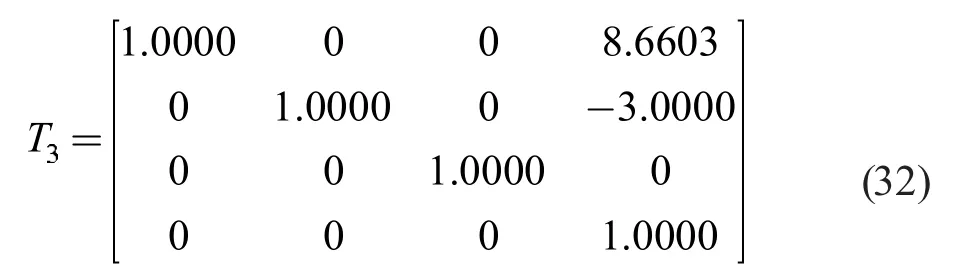
因此,機(jī)構(gòu)的位置反解正確,即式 (29)為CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)的位置反解。

將該機(jī)構(gòu)在ADAMS 軟件中進(jìn)行仿真分析驗(yàn)證,驗(yàn)證了該機(jī)構(gòu)確實(shí)具有三個(gè)自由度,并得處分支三的運(yùn)動(dòng)軌跡曲線和計(jì)算一直,自由度驗(yàn)證結(jié)果見圖4,分支三的運(yùn)動(dòng)軌跡曲線見圖5。

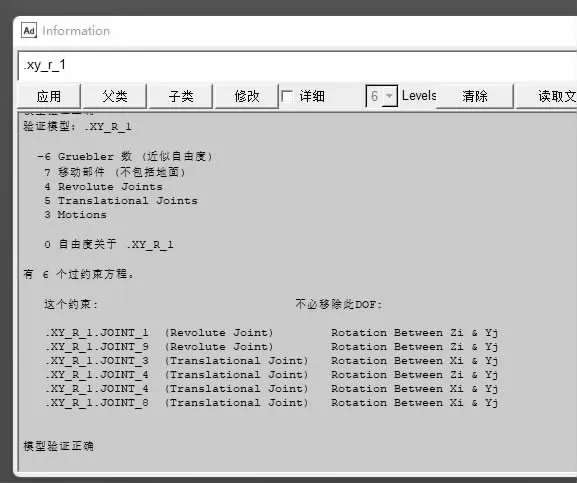
圖4 自由度驗(yàn)證結(jié)果

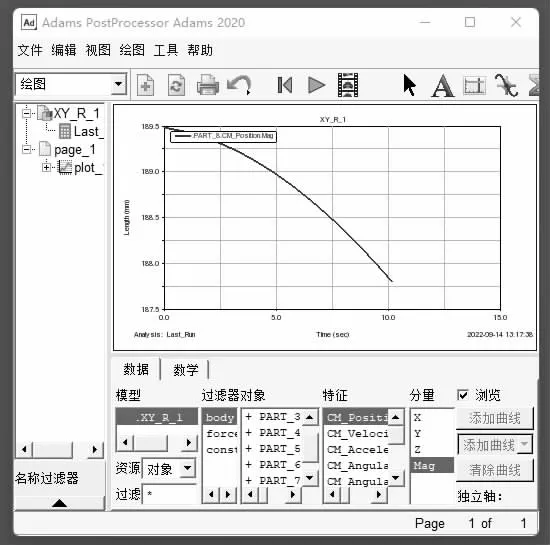
圖5 分支三運(yùn)動(dòng)軌跡曲線

5 結(jié)論

（1）分析CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)的結(jié)構(gòu),應(yīng)用螺旋理論,給出該機(jī)構(gòu)位置反解的整個(gè)推導(dǎo)過程。

（2）得出CPP-RPP-PRR 解耦并聯(lián)機(jī)構(gòu)的位置反解求解公式,并進(jìn)行特殊位置驗(yàn)證,為該機(jī)構(gòu)進(jìn)一步的速度分析、加速度分析、受力分析、誤差分析、工作空間分析、動(dòng)力學(xué)分析和機(jī)構(gòu)綜合等奠定了理論基礎(chǔ)。