無線傳感網移動數據采集效果提升方法*

楊倩倩，王 龍

(晉中信息學院大數據學院，山西 太谷 030800)

大數據技術的發(fā)展與進步提高了數據處理的效率[1]，增加了人們在日常生活和工作中的認知盈余，開拓了眼界，拓寬了視野。 但隨著大數據網絡時代信息的不斷發(fā)展[2]，數據積攢越來越多，造成可使用數據被海量冗余數據覆蓋，長此以往將會導致諸多不良影響，因此需智能采集移動數據，以提高數據采集效果。

史兵麗等[3]設計了基于ZigBee 無線網絡的應變數據采集系統，并結合調制協調器和FPGA 陣列完成數據采集。 Karthikeyan A 等[4]指出由于信號覆蓋的環(huán)形范圍導致三維無線傳感器網絡數據重復，為此，制定了三維分散分組(3D-SG)方案，根據該方案實現了數據采集與評估。 陳琪等[5]將所有節(jié)點均勻劃分成簇，然后在簇內采用節(jié)點分級的思想進行數據的多跳傳輸，最后使用移動采集器沿著最短路徑訪問簇頭節(jié)點完成數據采集。 上述三種方法雖然都實現了數據采集，但是由于移動節(jié)點具有較高的隨機性，因此在采集過程中無法對其進行較為準確的對比，導致數據采集效果有待進一步提升。

在上述分析的基礎上，本文在利用已有的LEACH 分簇算法完成移動數據節(jié)點分類采集的基礎上，利用最小生成樹方法分配移動數據采集時隙，以降低無線傳感網中的節(jié)點能量消耗，提升移動數據采集效果。

1 無線傳感網絡數據采集

1.1 信息熵權重計算

首先，將未完成聚類[7]的節(jié)點數據對象的數目設為N，且所有未完成聚類對象的屬性采用G+P維來表示，結合變化不定的數據信息，構建如下信息數據集U:

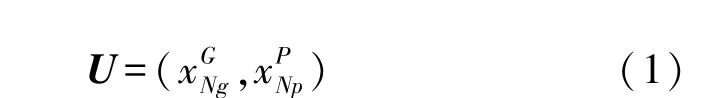
由于量綱的不同，WSN 中節(jié)點數據信息具有一定的隨機性，因此無法對其進行較為準確的對比。要使不同量綱的數據對象能夠相互比較，就必須采用正規(guī)的無量綱化預處理方法，具體為先使用無量綱化法對節(jié)點數據進行處理，再將處理結果投影到[0，1]區(qū)間內，計算方法如下式:

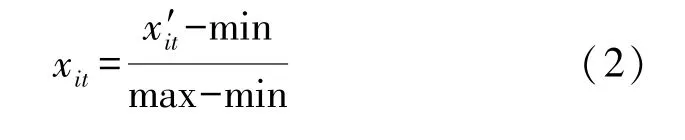
式中:xit代表在處理前的某維屬性，而x′it則代表處理后的某維屬性，min 代表這一維屬性數據中的最小值極限，max 代表這一維屬性數據中的最大值極限。

式中:Ht代表在所有維的屬性中節(jié)點數據的熵值。如果xit相對于預先指定的t的值完全相等，則有

1.2 繪制等勢線

1.2.1 計算勢值

當WSN 是由雙重屬性數據對象組成時，任意一個WSN 中節(jié)點xi對于節(jié)點xj處所產生的勢值可表示為:

1.2.2 查找空勢心

一般空間位勢中心位于同一類簇的中心，類簇的空間中心是該類節(jié)點數據對數據空間中某一概念的附屬中心，也是該概念特征的節(jié)點數據聚集中心。此外，在無線傳感網絡數據場中，空間勢心是一種用物體來表示的客觀實體節(jié)點數據，即由傳感器節(jié)點在物理空間的位置屬性和感知屬性構成。

采用LEACH 分簇算法將整個無線傳感器網絡節(jié)點劃分為K個聚類范圍，作為聚類核心的LEACH分簇算法實現了移動Sink 數據采集方案[9]的空間分布均衡。

以確定的無線傳感網絡節(jié)點的物理位置質心坐標為基礎，依據質心點之間的最小歐氏距離原理和剩余能量不低于平均能量原則，確定各個聚類中移動數據采集點。

勢能函數[10]是指在整個力場中，勢能依賴于位置和距離的函數。 在一個由雙重屬性數據對象組成的WSN中，決定在節(jié)點數據空間U中進行聚類，劃分為K個類{Π1，Π2，…，Πk}，此簇內所有對象的勢能相加之和與該簇內對象總數量之間的比值就是劃分簇的平均位值ˉφ(K)，以上述確定的空勢心為基礎，將ˉφ(K)表示為:

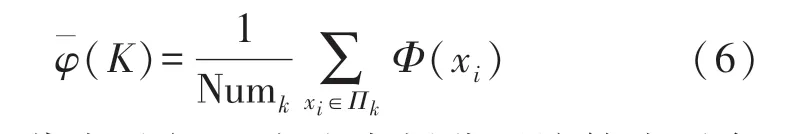
式中:NumK代表進行K個聚類劃分后該簇內對象總數量，Φ(xi)代表任意一個WSN 在xi處的位值和其他WSN 節(jié)點在xi處產生的位值的乘積。

WSN 數據場中的等勢線被認為是空間勢心所環(huán)繞。 即在疊加過程中點數較大的節(jié)點數據形成的勢心是一種接近目標數值的節(jié)點數據，而節(jié)點的數據在疊加時比疊加之前較小數值的節(jié)點數據起到了更大的作用。 因此根據上述計算結果繪制等勢線，為無線傳感網絡數據采集奠定了良好基礎。

1.3 完成數據采集

使用LEACH 分簇算法[11]劃分無線傳感網絡區(qū)間后，網絡中所有傳感器節(jié)點的聚集節(jié)點即為聚類中的數據采集點，因此本文選取二維Dubins 曲線[12]實現所有采集點的連線。

其中，RSL 型Dubins 曲線主要包括三段，即:

式中:φ0代表聚類區(qū)間的切線內夾角，φ1代表聚類區(qū)間的切線外夾角，d代表各個聚類區(qū)間之間的距離，sinφ0代表聚類區(qū)間的切線內夾角的正弦值，cosφ0代表聚類區(qū)間的切線內夾角的余弦值，sinφ1代表聚類區(qū)間的切線外夾角的正弦值，cosφ1代表聚類區(qū)間的切線外夾角的余弦值，arctan 代表反正切函數，mod 代表求余函數，｜L｜、｜S｜和｜R｜分別表示RSL 的三段曲線長度，相加可獲得完整的Dubins曲線的長度，即:∮LRS=｜L｜+｜S｜+｜R｜。

在分簇數據的基礎上采用Sink 數據對節(jié)點再進行細分，其細分后節(jié)點構成了Dubins 曲線，從而有序快速地采集數據。

綜合上述分析，本文移動數據采集流程如圖1所示。

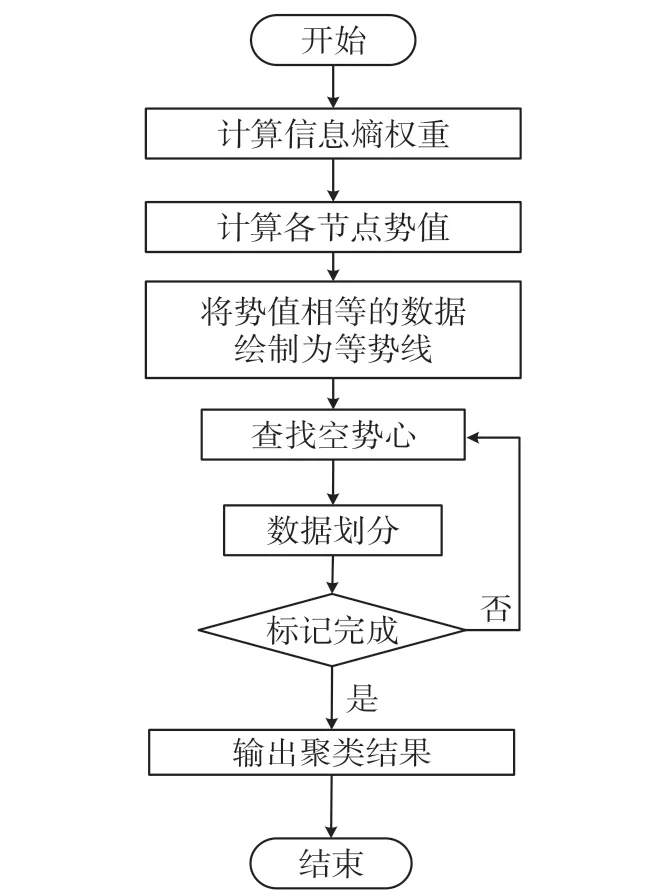
圖1 無線傳感網移動數據采集流程圖

至此完成無線傳感網絡移動數據采集。

2 數據采集效果提升方法

2.1 基于節(jié)點剩余能量的最小生成樹

為了進一步優(yōu)化無線傳感網數據效果，本文利用節(jié)點剩余能量作為邊權重，再利用克魯斯卡爾(Kruskal)算法構建最小生成樹[13-14]。

假設無線傳感網數據連通網N=(V，E)，將N中的邊按權值從小到大的順序排列:

①初始狀態(tài)為只有n個頂點而無邊的非連通圖T=(V，{})，圖中每個頂點自成一個連通分量。

②在節(jié)點能量E中選擇權值最小的邊，若該邊依附的頂點落在T中不同的連通分量上(即不形成回路)，則將此邊將入到T中，否則舍去此邊而選擇下一條權值最小的邊。

③重復步驟②，直到T中所有的頂點都在同一連通分量上為止。 由此得到最小生成樹示意圖，如圖2 所示。

圖2 最小生成樹示意圖

圖2 中數字為節(jié)點剩余能量。 如節(jié)點2 的剩余能量為30。 依據節(jié)點剩余能量計算邊權重，每條邊權重等于邊的兩端節(jié)點剩余能量之和。 如由節(jié)點5和節(jié)點2 構成的邊，其邊權重為20 與30 的和，即50。

2.2 分配時隙的流程

先利用Kruskal 算法構成生成樹，然后給樹中的每個節(jié)點分配時隙，分配過程的偽代碼如下:

①把原圖中所有邊按權值排序

②初始化最小生成樹為空，以及初始化連通分量

③for(intn=?；n＜N；n++)

④if(E[n]?T=(V，{ }){

⑤把邊E[n]加入最小生成樹

⑥合并E[n]所在的連通分量

⑦}

至此完成無線傳感網移動數據采集效果提升。

3 仿真與結果

為了驗證無線傳感網移動數據采集效果提升方法的整體有效性。 分別用本文方法、文獻[3]方法和文獻[4]方法進行如下測試。

3.1 仿真準備

使用MATLAB 軟件建立仿真平臺。 考慮200個無線傳感網絡節(jié)點隨機分布于500 m×500 m 區(qū)域。 每個節(jié)點的通信半徑為50 m。 200 個節(jié)點內只有部分節(jié)點在每輪產生數據包，即產生數據包的概率從0～1 變化。 具體參數設置如表1 所示。每當移動節(jié)點移動到終點并返回起點時，稱其完成一“輪”移動。 根據移動節(jié)點的通信范圍，可以將全部區(qū)域劃分為直接通信區(qū)域和多跳通信區(qū)域。

表1 仿真參數設置

圖3 中，L1 和L2 兩條曲線之間的區(qū)域即為直接通信區(qū)域，該區(qū)域內的節(jié)點距離軌道較近，因而能夠向移動節(jié)點直接傳送數據。 而無線傳感網中的其他節(jié)點需要采用多跳中繼方式將數據傳送給區(qū)域內節(jié)點。

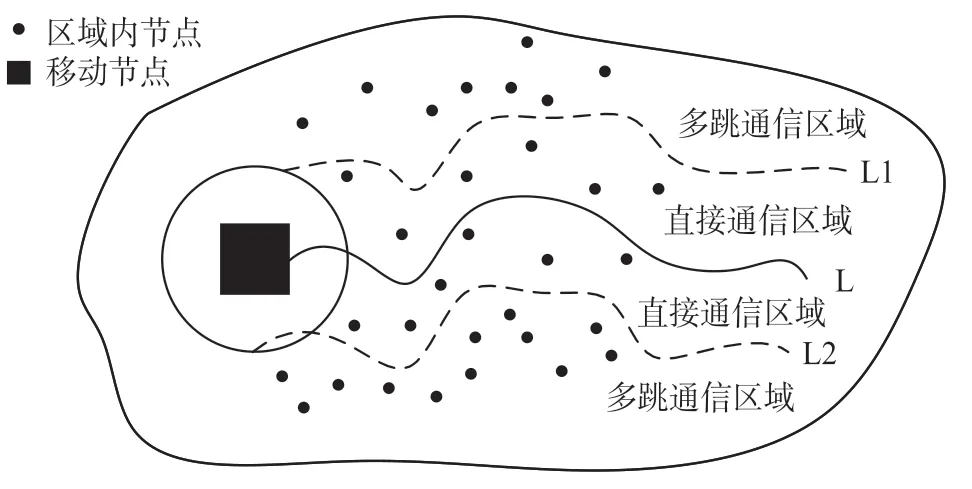
圖3 應用場景示例圖

3.2 仿真結果與分析

3.2.1 質心坐標查找準確性測試

根據上述參數設定，考慮到不同方法適用場景不同，因此利用式(3)計算信息熵權重，并以0.85 作為固定值，設置移動節(jié)點坐標為(118，89)，測試三種方法查找節(jié)點的物理位置質心坐標的準確性。 其測試結果如圖4 所示。

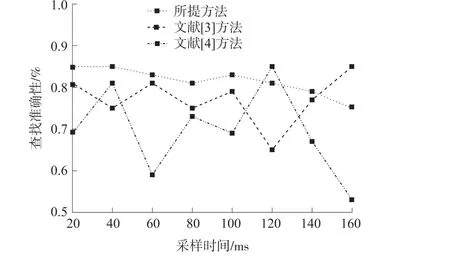
圖4 不同方法質心坐標查找準確性對比

由圖4 可知，采用所提方法、文獻[3]方法和文獻[4]方法的質心坐標查找準確性相差均較小，所提方法和文獻[3]方法最高差值均為0.10%，文獻[4]方法最高差值為0.16%。 整體來看，所提方法整體質心坐標查找準確性曲線波動幅度較小，表明所提方法的質心坐標查找誤差是三種方法中最低的。 這是因為所提方法結合了信息熵權重，使用勢能函數對節(jié)點數據對象進行分簇，提高了方法的質心坐標查找準確性。

3.2.2 能耗測試

假設本文所研究的無線傳感網中節(jié)點的初始能量設置為30 J，結合Kruskal 最小生成樹算法流程，構建能耗模型如下:

由圖5 可知，在相同的有效測試次數下，所提方法的能耗量均在0.06 ～0.07 的最佳區(qū)間內，且隨著測試次數的增多，數據采集的能耗量也在隨之下降。雖然文獻[3]方法的數據采集能耗量和文獻[4]方法的數據采集能耗量也在隨之下降，但能耗區(qū)間與所提方法的最佳能耗區(qū)間相比過高，這是因為所提方法利用Kruskal 算法構成最小生成樹，然后給樹中的每個節(jié)點分配時隙，促使每個節(jié)點得到的實時能耗量最低，較低的能耗量進一步增強了采集的穩(wěn)定性，這充分驗證了所提方法的有效性。

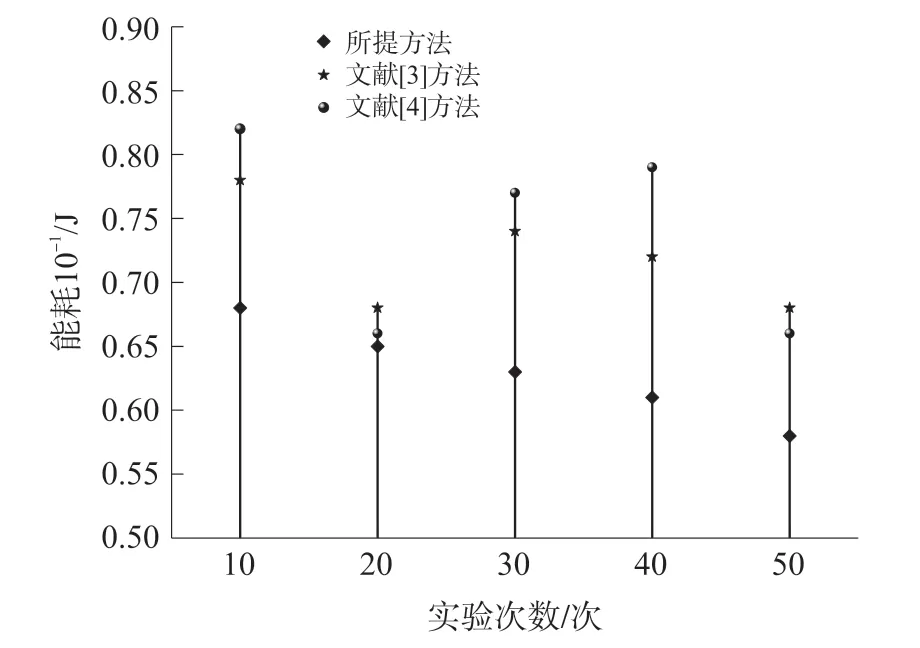
圖5 不同方法數據采集能耗量對比

3.2.3 延時率測試

對比三種方法在發(fā)送采集移動數據時產生的延時率，延時率等于數據幀長度和發(fā)送速率的比值，延時率越低，數據采集后的傳輸效果越好。 對比結果如表2 所示。

表2 不同方法數據采集的延時率

由表2 可知，在多次有效測試后，所提方法的延時率均在20%以下，而文獻[3]方法和文獻[4]方法的延時率都在25%以上，這是因為所提方法首先對無線傳感網絡數據進行聚類處理，將需要采集的數據提前聚類，提高了采集效率，降低了延時率。 通過上述對比，驗證了所提方法的有效性。

4 結束語

近年來，由于可循環(huán)有效數據資料的流失對日常生活造成了許多不便，因此需要對聚類移動數據進行智能采集。 目前無線傳感網數據采集方法的采集效果有待進一步提升，所以提出無線傳感網移動數據采集效果提升方法。 利用無線傳感網絡構成勢值等勢線，采用LEACH 算法聚類，然后將聚類后的節(jié)點數據構成Dubins 曲線完成數據采集，最后通過構建最小生成樹分配數據收集時隙。 由仿真結果可知，所提方法解決了數據采集誤差大、數據采集效率低、數據采集所用能耗大、數據采集的延時率高的問題，為將來數據智能化采集奠定了基礎。