裝配應力對六維力傳感器性能的影響研究

屈震龍，相立峰，李晨，王周義，戴振東

(1. 南京航空航天大學 機電學院，江蘇 南京 210016； 2. 南京神源生智能科技有限公司，江蘇 南京 211215)

0 引言

信息的精準、快速感知是智能化工業發展的重要保障[1]。接觸過程在加工、制造、生產等行為中普遍存在。因此，利用多維力傳感器來實現接觸作用力的精準、快速測量在智能制造、國防工業和前沿科學等領域具有重要意義[2]。

在基于不同原理的多維力傳感器中，電阻應變式的多維力傳感器因兼具較好的靜、動態性能和成本等優勢而受到研究人員的廣泛關注[3]。電阻應變式力傳感器的技術核心是測量結構彈性應變來獲得載荷(力或力矩)。因此，電阻應變式力傳感器在使用過程中應盡可能地降低非待測載荷導致的應變來保障測量可靠性。

然而，由于受加工誤差、安裝定位偏差等因素影響，力傳感器彈性體在與其他結構連接、裝配過程中不可避免地會產生裝配應力。此外，為避免使用過程中意外損害傳感器內部結構和電路，通常需要對傳感器彈性體進行封裝。封裝過程也不可避免地會導致裝配應力。這些裝配應力屬于典型的非待測載荷，輕則引起傳感器彈性體初始變形，導致其靜、動態性能變化；重則導致結構破壞，造成傳感器永久損傷。因此，裝配應力的影響是力傳感器使用過程中必須考慮的問題。

本團隊在前期研究中研發了一種圓柱形電阻應變式六維力傳感器，實現了三維力和三維力矩的高精度低耦合測量，并為該六維力傳感器設計了專門的結構，一方面對傳感器進行封裝，另一方面起到力傳遞作用。本文通過仿真和實驗分析的方法對該封裝裝配過程進行了研究，力圖明確裝配應力對其性能的影響規律，找到合適的裝配方法，保證六維力傳感器的性能，并為其他類型六維力傳感器的研制和使用提供參考。

1 六維力傳感器及其封裝設計

用于本文研究的六維力傳感器彈性體如圖1(a)所示[4]。設計量程為Fx=Fy=±300 N，Fz=±600 N，Mx=My=Mz=±25 Nm，應變片貼片及組橋如圖1(b)、圖1(c)所示。根據理論設計計算：各方向空載時電橋讀數應變為0，滿載時讀數應變分別為εFx=εFy=1073.4 με，εFz=1022.6 με，εMx=εMy=2125.4 με，εMz=1204.3 με。

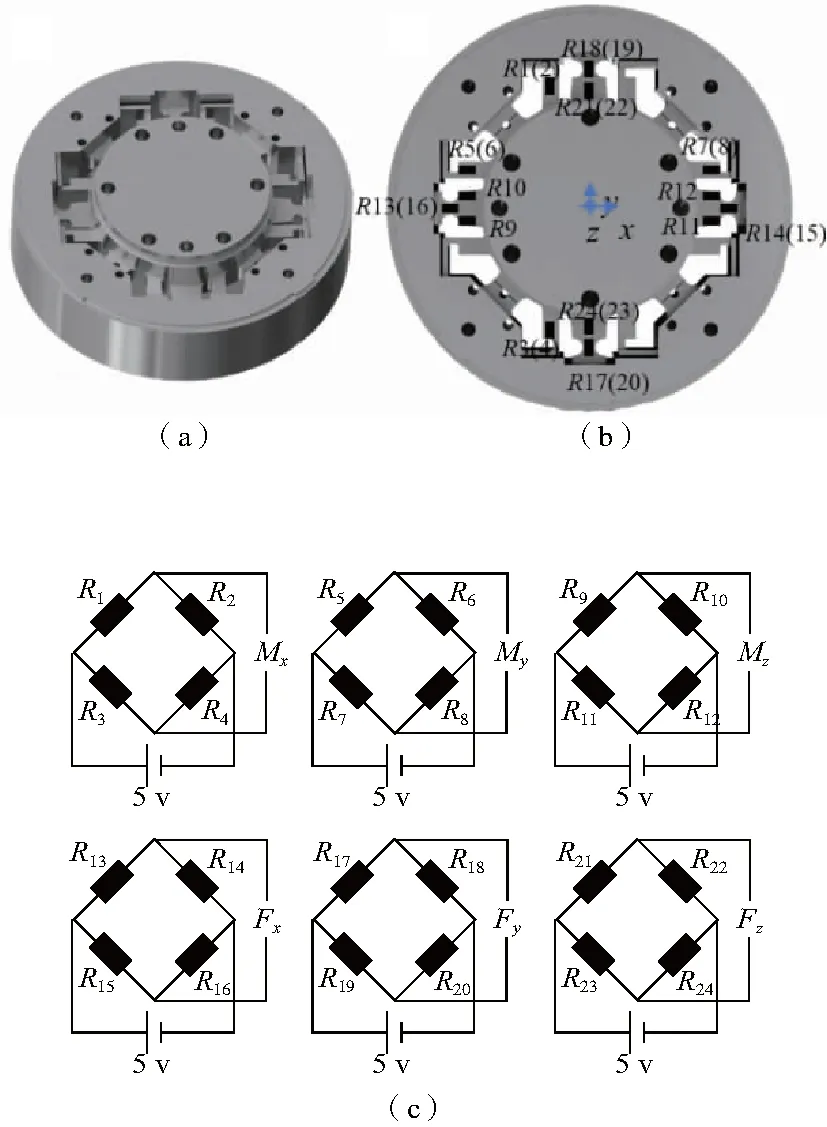
圖1 六維力傳感器結構、貼片及組橋示意圖

六維力傳感器設計的封裝結構如圖2(a)所示。下蓋板(圖2(b))不僅起到封裝作用，還起到連接彈性體與基座的作用。與彈性體之間的連接必須緊固可靠，實際操作中通過8枚M5的螺栓來聯接。為了保證裝配定位，設計了兩枚φ4的定位銷。首先依次施加2.5 Nm的預緊轉矩來預緊螺栓，然后依次施加5 Nm的擰緊轉矩來緊固螺栓。

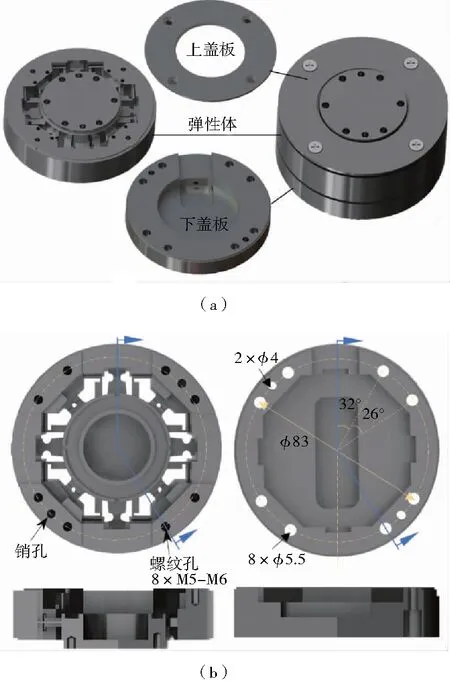
圖2 六維力傳感器封裝設計

2 裝配過程仿真分析及測試

2.1 有限元模擬

本文首先利用有限元法(Abaqus 6.14)模擬下蓋板與彈性體的裝配過程。分析中螺紋連接過程直接簡化為力和力矩作用。螺紋夾緊力F可以用經驗公式(1)來計算[4]：

(1)

式中：T是總轉矩；k是轉矩系數，本文選取0.2；D是螺紋公稱直徑。

參照機械設計手冊[4]，假定下蓋板與螺栓端面接觸區域承受總轉矩的50%，彈性體螺紋部分承受總轉矩的40%，二者之間承受一對擠壓力。螺紋連接的載荷可以等效為表1所示的情形。

表1 有限元分析的載荷情況

彈性體和下蓋板的材料均為鈦合金，彈性模量E=107.8 GPa、泊松比v=0.34、密度為ρ=4510 kg/m3、屈服強度≥895 MPa。

螺紋連接的裝配過程中，裝配順序的影響是工程人員關心的重點之一。本文考慮了3種裝配加載順序：1)從銷附近的螺紋孔開始，先順時針預緊所有螺紋，然后反向擰緊所有螺紋，文中體現為2—3—4—5—6—7—8—1(預緊)/1—8—7—6—5—4—3—2(擰緊)；2)從遠離銷孔螺紋開始，按照對角方式預緊和擰緊螺紋，文中體現為4—8—2—6—3—7—5—1(預緊)/4—8—2—6—3—7—5—1(擰緊)；3)從銷孔附近螺紋開始，按照對角順序預緊和擰緊螺紋，文中體現為7—3—4—8—5—1—2—6(預緊)/5—1—2—6—4—8—3—7(擰緊)。有限元模型中將每一個螺紋孔的載荷設定為一個分析步。

此外，本文通過兩種方式進一步探索摩擦力對裝配應力的影響：①將下蓋板與彈性體之間的摩擦系數設定為變量(0.1、0.2、0.3)；②改變名義接觸區域的大小。

2.2 實驗測試

參照有限元分析結果，本文對實際傳感器進行了測試。采用自研的信號調理采集系統記錄按照不同順序擰緊螺栓時六維力傳感器各個方向的輸出變化，以探究裝配過程的影響。

3 結果及討論

圖3示意了按照7—3—4—8—5—1—2—6(預緊)/5—1—2—6—4—8—3—7(擰緊)順序模擬裝配加載時測量Mx的電橋中各應變片(R1-R4)貼片區域及附近的應變變化規律，摩擦系數設定為0.2。圖中紫色區域示意了名義接觸面。灰色條示意了貼片位置(本刊黑白印刷，相關疑問請咨詢作者)。根據電阻應變片的工作原理，可以認為電阻應變片測量的結果是敏感柵所在區域內應變的平均值[5]。為此，可以計算整個模擬過程中各個方向測量電橋中各個應變片的平均應變及各個電橋的讀數應變，以進一步量化裝配過程的影響。

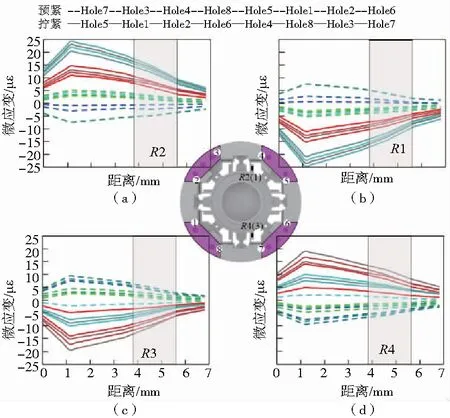
圖3 一組典型的有限元分析結果

3.1 螺紋加載順序的影響

從圖4的結果可以看出，對于同一種加載順序，不同端面摩擦系數條件下各個方向零漂的變化規律相似。此處以端面摩擦系數為0.2為例，討論裝配加載順序的影響，端面摩擦系數的影響將在下一節中討論。

采用第1)種加載順序加載時傳感器彈性體各方向的零漂如圖4藍線所示。預緊階段Fx方向零漂先增加然后減小，然后又再次增加。擰緊階段的變化過程與預警階段相類似，最終為-44.9 με(圖4(a))。Fy方向的零漂預緊階段先增大后減小，而擰緊階段先減小后增大。最終的讀數應變零漂為理論滿量程值的-0.2%(圖4(b))。Fz方向零漂在整個加載過程中幾乎持續增加，最終的零漂占滿量程值的4.2%(圖4(c))。Mx方向零漂也總體呈現出增加的趨勢，加載完成后的應變零漂為13.7 με(圖4(d))。My方向零漂總體上保持不變，最終結果為理論滿量程值的-0.2%(圖4(e))。Mz方向零漂在加載過程中波動較大，但最終結果僅為理論滿量程值的0.3%(圖4(f))。

采用第2)種方式加載時彈性體各方向零漂與載荷步的關系如圖4橙紅色線所示。Fx方向應變零漂在預緊和擰緊階段均先增大后減小，最終為-53.8 με(圖4(a))。Fy方向的應變零漂總體上幾乎保持不變，僅有理論滿量程值的0.5%(圖4(b))。Fz方向的應變零漂隨著載荷步的進行而增加到31.9 με(圖4(c))。Mx方向應變零漂在預緊和擰緊階段均先減小后增加，最終回復到理論滿量程值的0.4%(圖4(d))。My方向應變零漂變化規律與Mx方向相反，最終結果為理論滿量程值的-0.2%(圖4(e))。Mz方向應變零漂值在預緊階段和擰緊階段均表現為小幅增加—減小—增加。載荷步結束后的結果僅為設計滿量程值的-0.1%(圖4(f))。

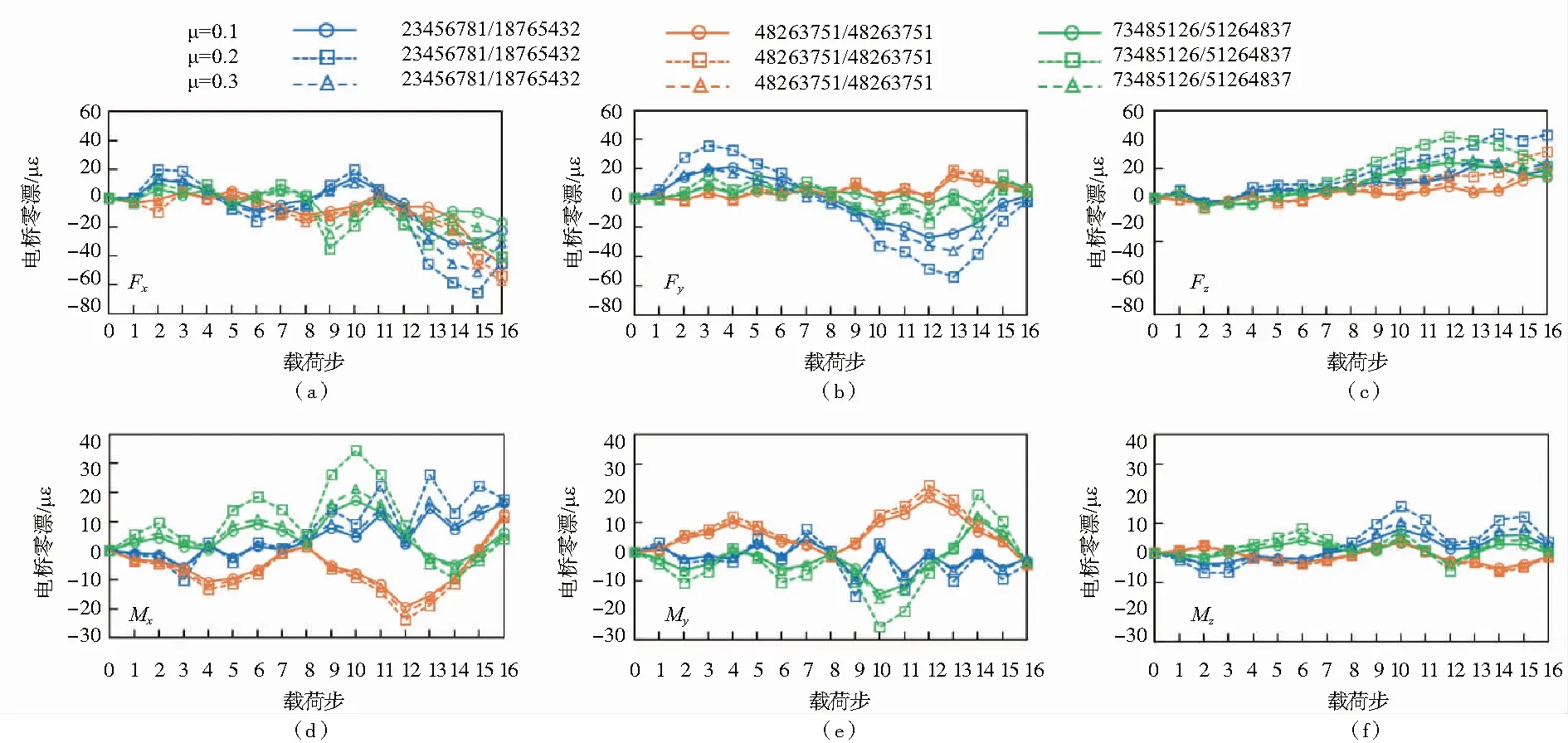
圖4 不同摩擦系數條件下不同加載順序裝配有限元分析結果

采用第3)種加載順序加載時傳感器各方向讀數應變的零漂變化結果如圖4綠線所示。Fx方向應變零漂變化在預緊階段和擰緊階段具有一定的相似性，經歷了“增大—減小—再增大—再減小”的變化過程，最終結果為-40.4 με(圖4(a))。Fy方向應變零漂值在預警階段總體上先增加后減小，而在擰緊階段則先減小后增加，最終結果僅為設計滿量程應變的0.4%(圖4(b))。Fz方向應變零漂變化與Fy相反，最終結果為21.8 με(圖4(c))。Mx方向應變零漂在預緊階段前4個載荷步和后4個載荷步均先增加后減小，但在擰緊階段前4個載荷步先增大后減小而后4個載荷步先減小后增大(圖4(d))。My方向應變零漂的變化規律與Mx方向相反，最終的結果為-3.7 με(圖4(e))。Mz方向應變零漂最終結果幾乎可以忽略(0.8 με)。

上述有限元分析結果與實測結果(圖6中實線)具有高度相似性。但從數值上看，實際測量的結果要比理論分析的結果略小。可能的原因包括：①有限元模型中各部分的尺寸都是理想的，而加工件可能存在一定加工誤差；②加工件接觸面的摩擦系數與分析中的設定值有所差異。

3種不同加載方式在載荷步進行過程中均會導致傳感器各方向的零漂。但總體來說，第3)種裝配加載順序的零漂最小，第2)種次之，第1)種最大。

3.2 觸端面摩擦系數的影響

圖4中的實線和虛線還分別展示3種接觸端面摩擦系數(0.1、0.2和0.3)條件下的分析結果。從圖4的結果來看，當接觸端面的摩擦系數發生變化時，各個方向的零漂變化規律相似。

在研究開始之前，曾猜測摩擦系數越大，裝配應力的影響越大。然而，有限元分析的結果表明，摩擦系數為0.1時裝配應力對傳感器零漂的影響最小(圖4實線，圓形記號)；當端面的摩擦系數增加至0.2時，3種裝配順序下裝配應力導致的零漂均增加(圖4虛線，方形記號)；然后，當端面摩擦系數繼續增加至0.3時，裝配應力導致的零漂并未繼續增大，反而減小(圖4，虛線，三角形記號)，但比摩擦系數為0.1時略大。這可能是由于傳感器彈性體內部特殊的結構導致的。該過程涉及復雜的力學行為，還需要進一步深入研究。同時，這也啟示了在實際過程中應該充分考慮裝配體之間摩擦系數的影響。

3.3 接觸端面大小的影響

本文還按照前述3種加載方式分別模擬了接觸端面全接觸和部分接觸時裝配情形，結果如圖5所示。在此分析中，接觸面的摩擦系數設定為0.2。分析結果表明，在同一種加載方式下，接觸端面面積不同時傳感器彈性體電橋的輸出應變(零漂)理論值的變化規律相似，但總體上看，接觸端面面積較小時裝配應力導致的電橋零漂較低(圖4虛線)。

為了驗證上述理論分析結果，利用同種工藝條件和加工手段加工了兩種Ti合金彈性體和蓋板并進行了裝配測試，結果如圖6所示。測試結果表明：接觸端面面積增大，零漂增大。圖4和圖5的結果比較發現，實際測試中傳感器零漂的變化規律與有限元分析的結果具有一定的相似性，但又不完全吻合。

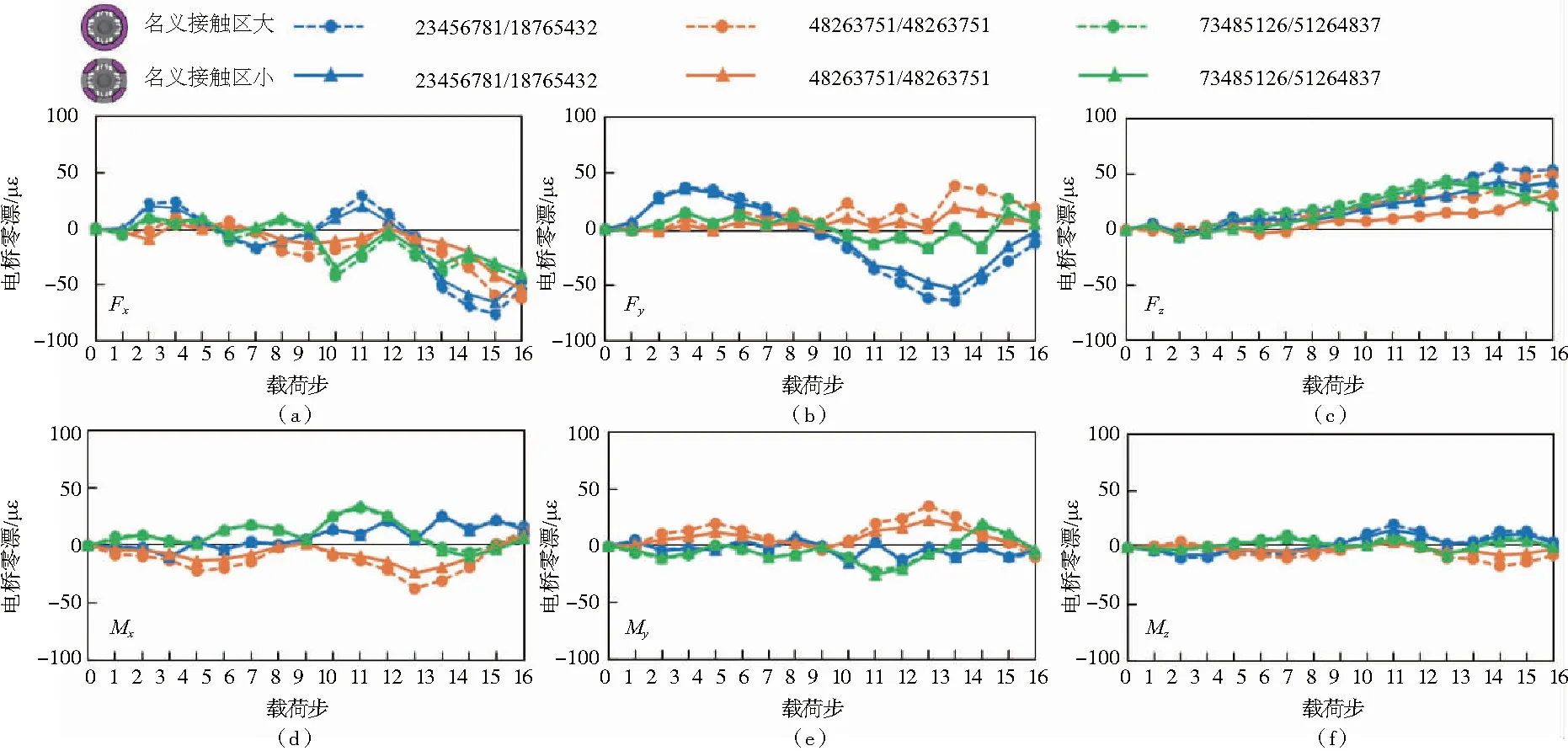
圖5 不同接觸端面大小模型裝配過程有限元分析結果

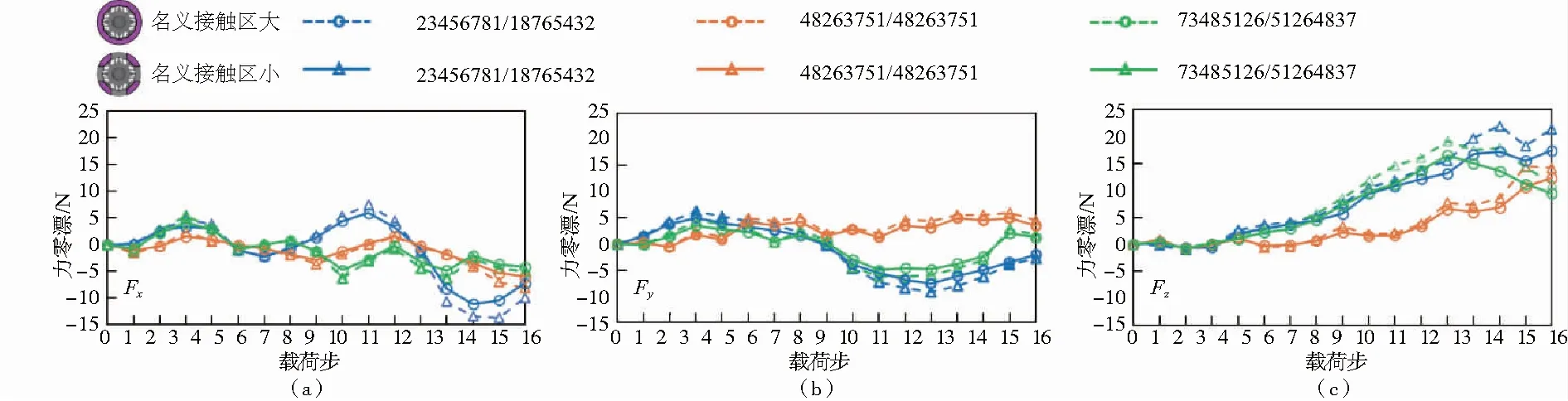
圖6 不同接觸端面大小模型裝配過程實際測試結果

仿真結果表明接觸端面大時，3種方式加載裝配過程導致的零漂最大可達5.8%F.S.(Full Scale)；而接觸端面小時，3種方式加載裝配過程導致的零漂最大為5% F.S.。而實測的結果表明，接觸端面大時3種方式加載裝配過程導致的零漂最大可達3.6%F.S.，而接觸端面小時3種方式加載裝配過程導致的零漂最大為2.9% F.S.。

在剛體研究中，摩擦力與接觸面積無關。然而，本文中研究的模型材料并非是完全剛性的材料。因此，摩擦力可能會受到接觸面積(接觸變形)的影響。此外，本文的裝配應力是由于彈性體和蓋板的變形不一致導致的。在二者接觸過程中，接觸面會產生摩擦力，而摩擦力在一定程度上也可以看作是驅使二者變形的載荷。因此，減少接觸區能夠減少摩擦力的作用區。與有摩擦力時相比，這些區域上的變形會產生一定變化，最終影響傳感器的輸出零漂。

理論分析結果和實際測量結果的相似性表明：對于本文的多維力傳感器，減小與蓋板接觸面的面積能在一定程度上減小裝配應力的影響。

4 結語

本文通過有限元模擬和實際測試研究了裝配過程對一種螺紋連接的圓柱型六維力傳感器零漂輸出的影響。研究發現，為了盡量降低裝配應力導致的零點漂移，在裝配時應該考慮如下因素：

1)有銷存在時，應該盡可能地從銷附近的螺紋開始加載，并按照對角原則選擇加載螺紋；

2)應該充分考慮接觸區域摩擦系數的影響；

3)可以通過減小接觸面的方式減小裝配應力的影響。