H-VAWT翼型的拋物線翼型理論及氣動特性研究

張照煌，胡德鵬，高 迪

（華北電力大學 能源動力與機械工程學院，北京 102206）

0 引言

由于受到各種因素的影響，我國陸地與近海可規劃的風資源日趨緊張，高空和遠海將成為未來風電的主戰場[1]。風力發電機是利用風資源的主要裝置，從外觀與來流的位置可以將風力發電機分為水平軸風力機（HAWT）與垂直軸風力機（VAWT）。相 比 于HAWT，VAWT具 有 適 應 各 種 風向、結構簡單、安裝與維修方便且噪聲低、不需設置偏航機構以及對湍流適應性好等優點[2]。許多人認為，VAWT比HAWT度電成本高，無法商業化，但文獻[3]的研究表明，在大型海上風電場中，與HAWT相比，VAWT的風能利用率更高，風機排布更緊密，從而提高發電效率，降低度電成本。

葉片作為風力機捕獲風能的執行元件，是由展向不同位置的翼型積迭而成，葉片的氣動與結構特性由翼型直接決定，因此對于翼型的選擇和設計顯得至關重要。風力機專用翼型的設計多是針對HAWT設計出一系列氣動特性優良的帶彎度翼型[4]。但VAWT與HAWT有著不同的運行特點，在工作狀態下，VAWT的攻角變化范圍大，且葉片迎風面為吸力面和壓力面交替變換，故針對HAWT設計的翼型不能直接用于VAWT中。由此，對于VAWT翼型的設計顯得至關重要。目前，VAWT翼型的設計方法主要有正向設計法與反向設計法兩種[5]。李錦義[6]基于Joukowshi變形法和Trefftz構圖法結合弦線迎合運動軌跡的思想，提出了一種翼型設計的新方法。曲建俊[7]根據復合形式方法優化了氣翼，并獲得了幾個相對較好的氣翼。M Baghdadi[8]基于CFD優化技術，采用基于伯恩斯坦多項式的優化方法對葉片翼型進行了優化。陳曉田[9]提出了類函數與B樣條函數相結合的方法來表征翼型型線，結合粒子群優化算法并耦合翼型氣動性能預測RFOIL軟件對翼型氣動外形進行優化設計。

現有翼型的設計與優化均未從流動空氣與風電葉片相互作用機理的角度設計翼型。因此，本文提出一種針對H型垂直軸風力機 （H-VAWT）所用對稱翼型的新理論。基于風對葉片迎風面的作用機理使得空氣重量比擬壓差建立一種新的HVAWT翼型理論，即拋物線翼型理論。利用Matlab將拋物線可視化表達后旋轉取點形成翼型DAT格式文件，將文件導入內置XFOIL軟件的QBlade中數值模擬，并與H-VAWT常用的NACA4系列對稱翼型進行對比研究。

1 H-VAWT拋物線翼型理論的建立

流動的空氣微段ds吹向H-VAWT葉片迎風面，以理想狀態下H-VAWT葉片在45°為例（圖1），當其觸碰到葉片相應處的翼型線時，該微段空氣將沿此翼型線的切線方向向風電葉片尾緣運動。圖中，u為葉片線速度，v為風速。由于HVAWT中葉片攻角α頻繁變化且變化角度大，所以流動的ds的空氣壓差難以精確測量，但總存在某個大于0的常數C，使該流動的微段空氣壓差等于或近似等于該ds空氣的重量 Δmg與常數C的乘積。Δm為該微段空氣的質量，g為重力加速度。忽略空氣與風電葉片間的摩擦，則可將此微段空氣的流動看成是真空條件下在其前后壓差CΔmg作用下沿相應翼型線的運動，此流動過程中，該微段空氣的前后壓差所做的功轉化為其動能的增加量。

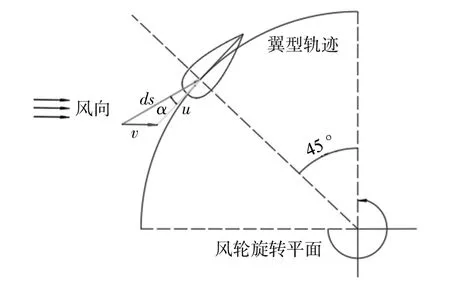
圖1 H-VAWT葉片受力分析圖Fig.1 H-VAWT blade force analysis diagram

設沿葉片表面流動的該微段空氣作用在其前后的壓差所做的功為Es，則：

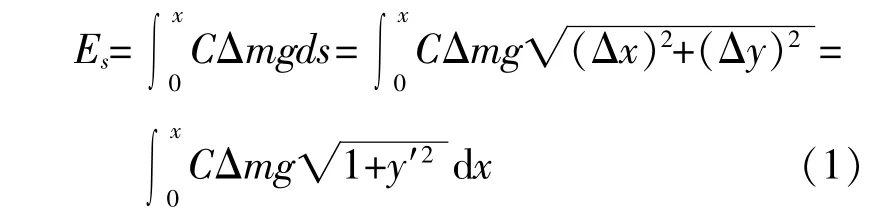
再設該微段空氣流過x橫坐標時，其動能的增加量為EE。

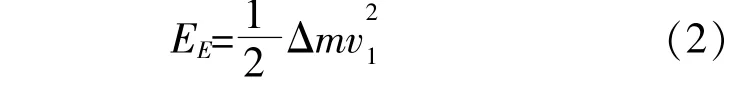
式中：v1為流動空氣微段在坐標x處時沿翼型線切線流動的速度。

根據上述分析，有：

將 式（1），（2）代 入 式（3），得：

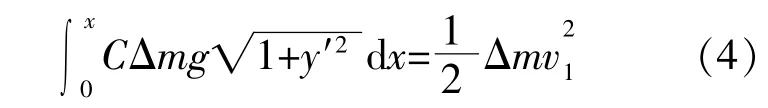
即：

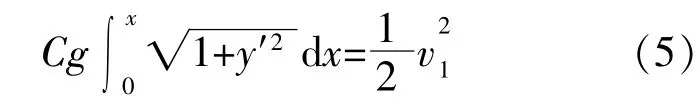
兩邊同時對x求導，得：

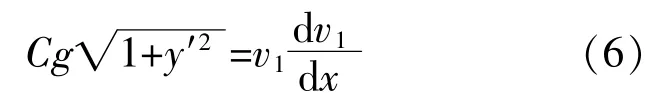
其中：

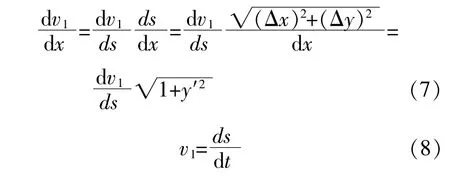
將 式（7）代 入 式（6），得：

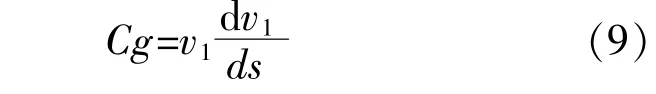
將 式（8）代 入 式（9），得：

在不考慮粘度的情況下，H-VAWT葉片翼型線上流動的空氣為以常數C倍的重力加速度為加速度做勻加速運動。流動空氣微段剛接觸或尚未接觸H-VAWT葉片的瞬時，由于其流動的速度方向正在發生變化，此時，從翼型線前緣沿該翼型線流動的初始風速應為0，則其運動規律可表示為

式中：s為空氣微段運動方程；t為空氣微段從翼型線前緣流動到后緣的時間。

圖2所示為空氣微段從翼型線前緣流動到后緣示意圖。

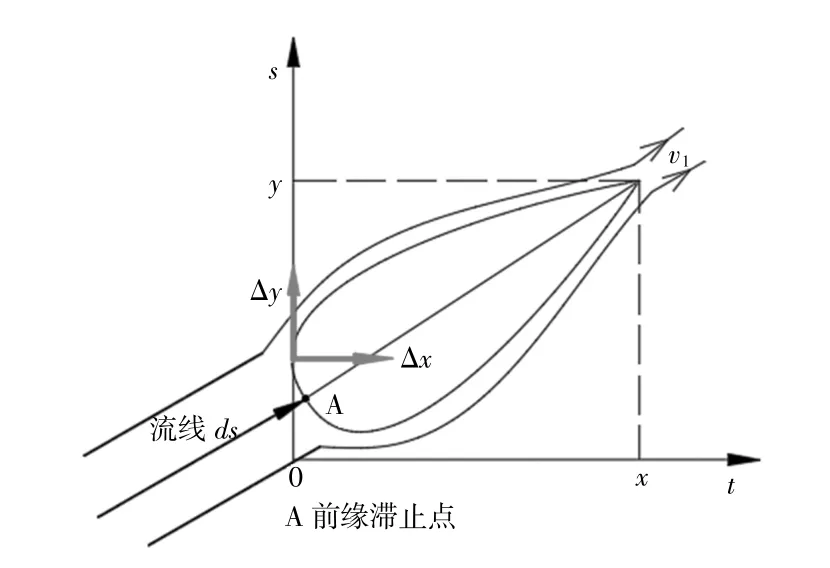
圖2 空氣微段從翼型線前緣流動到后緣Fig.2 Air flows from the leading edge to the trailing edge of the airfoil

流動空氣從H-VAWT葉片翼型前緣流動至其后緣，在時間t、路程s平面坐標系內的軌跡曲線為拋物線，以此曲線為H-VAWT葉片翼型線。該翼型線符合流動空氣在H-VAWT葉片表面的運動規律，可降低流動空氣的能量損失，從而提高H-VAWT葉片的風能捕獲能力。因此，可將以此種方法得到的翼型設計理論稱為H-VAWT對稱翼型的拋物線設計理論。

2 拋物線翼型母線的變化規律

H-VAWT的拋物線翼型理論是以流動空氣在風電葉片表面的流動規律為基礎建立的，以葉片旋轉到H-VAWT風輪的0°為例（葉片與風向平行）建立翼型。已知在拋物線函數中，C越大，函數變化越快，拋物線開口越小。為便于與HVAWT常用對稱翼型的氣動性能進行對比，本文采取以任意C值對應的拋物線為例，截取關于Y軸對稱且弦長為1的兩端拋物線圓弧[圖3（a）]，將兩端圓弧旋轉至X軸[圖3（b）]。鈍尾緣厚度與NACA4系列對稱翼型相似，取兩倍的0.01%t/c。將旋轉后的圖像稱為拋物線對稱翼型。

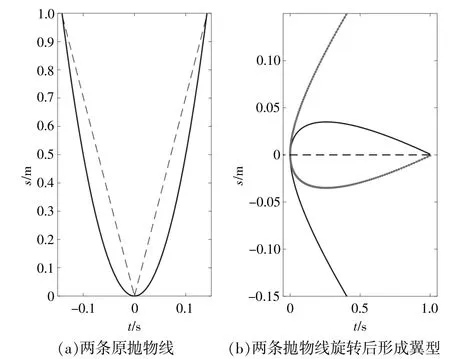
圖3 原拋物線及拋物線旋轉后形成翼型Fig.3 Parabola and parabolic airfoil

在此翼型上取點坐標后形成DAT格式文件，導入QBlade軟件中得到以不同常數C為母線的拋物線翼型。為避免翼型數據點個數差異對翼型氣動性能產生影響，出現的所有翼型數據點個數均一致。利用Matlab表達出不同常數C對應的拋物線翼型與其相對厚度間的關系（圖4）。

由圖4可知，由H-VAWT拋物線翼型理論得到的拋物線翼型母線的相對厚度隨常數C的增大先迅速增大到25%后逐漸收斂，最小相對厚度無限趨于0。這表明當兩點間的空氣壓差足夠大時，其流動規律趨于直線，符合實際情況。不同常數C的取值與其最大厚度位置間的關系如圖5所示。

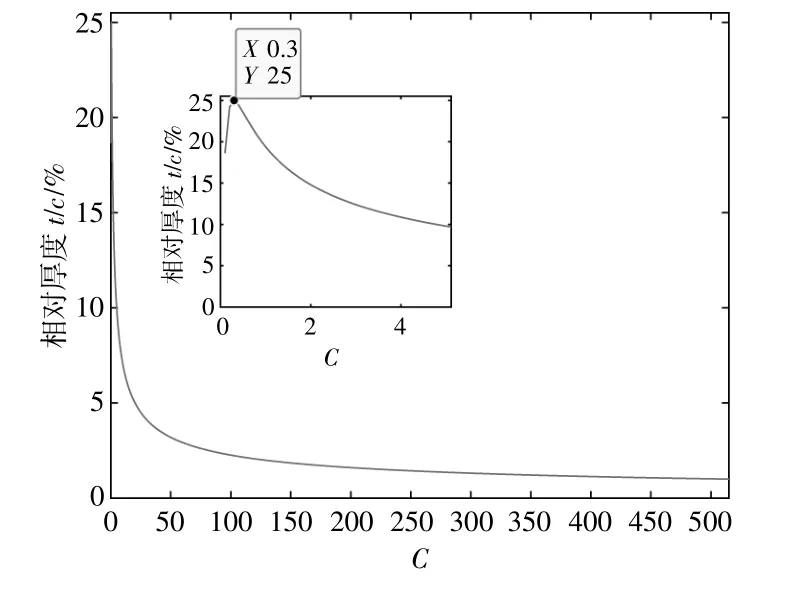
圖4 常數C與拋物線母線相對厚度間的關系Fig.4 The relationship between the constant C and the relative thickness of the parabolic bus

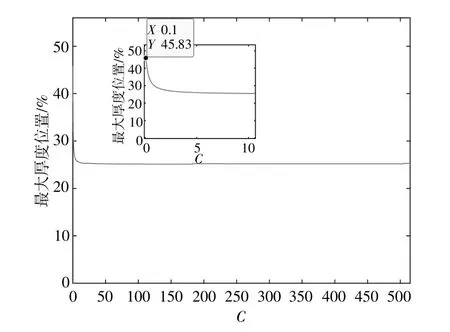
圖5 常數C與拋物線母線最大厚度位置間的關系Fig.5 The relationship between the constant C and the position of the maximum thickness of the parabolic bus

由圖5可知，隨著C的增大，拋物線翼型母線的最大厚度位置逐漸靠近前緣，最大厚度位于45.8%弦長處，最小厚度無限趨近于26%弦長處。

表1為選取的翼型母線相對厚度及最大厚度位置。隨著C值變化量越大，拋物線母線的相對厚度與最大厚度位置變化量越小，故規定C最大值 為515.07。

表1 選取的翼型母線相對厚度及最大厚度位置Table1 The relative thickness and maximum thickness position of the selected airfoil bus

續表1

3 拋物線翼型與NACA4 系列對稱翼型氣動特性對比

H-VAWT通常使用NACA4系列對稱的航空翼 型（特 別 是NACA0012，NACA0015和NACA 0018）。由于NACA0015翼型兼具優良的氣動與結構特性，故既可用于小型H-VAWT，又可用于大型H-VAWT。因此，以t/c=15%為例對兩種對稱翼型進行氣動性能的對比分析具有較為廣泛的實際意義。

拋物線翼型母線命名為PWX00xxMX，其命名規則與NACA4系列對稱翼型相似，其中PWX為拋物線首字母，MX為母線首字母，如：PWX0001MX-15表示相對厚度為1%，彎度為0在0%弦長處的拋物線翼型母線等比為相對厚度為15%的翼型。

文獻[10]表明了XFOIL可以真實地將風洞中的風環境狀態進行仿真和模擬。文獻[11]表明XFOIL對于翼型失速前區域已經有非常豐富的翼型理論和數據積累，因此翼型在附著流區域計算結果與實驗結果基本一致，當翼型進入失速發展區時，XFOIL計算結果與風洞實驗結果有較大偏差。

本文在確定參數前提下進行對比的所有翼型其失速攻角均在19°附近。氣動特性分析的攻角為0～20°，因此產生的計算誤差影響較小，可以忽略。利用Qblade軟件內置的XFOIL功能對表1中所選取的拋物線翼型母線等比成t/c=15%的翼型與NACA0015進行比較。在雷諾數Re=2000000，馬赫數Mach=0的有粘條件下，Ncrit=9的潔凈風洞條件下，對升力系數、阻力系數、最大升阻比在攻角為0～20°，步進為0.5°的條件下進行對比分析，所有翼型上下型線均取49個數據點，鈍尾緣厚度均一致。

圖6為t/c=15%時，PWX與NACA的升力系數對比曲線。

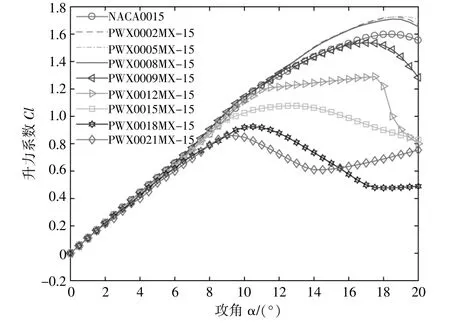
圖6 t/c=15%時，PWX與NACA的升力系數對比Fig.6 Comparison of lift coefficient between PWX and NACA when t/c=15%

由圖6可知：當拋物線母線的相對厚度小于9%時，所得到的拋物線翼型等比為t/c=15%時的最大升力系數均優于NACA0015，失速攻角均在19°附近且兩款翼型的升力系數隨攻角變化的趨勢一致；當攻角為0～10°時，兩款翼型的升力系數基本一致并均滿足線性關系；當攻角大于10°時，相對厚度小于9%的拋物線母線等比后的升力系數高于NACA0015。

圖7為t/c=15%時，PWX與NACA的阻力系數對比曲線。

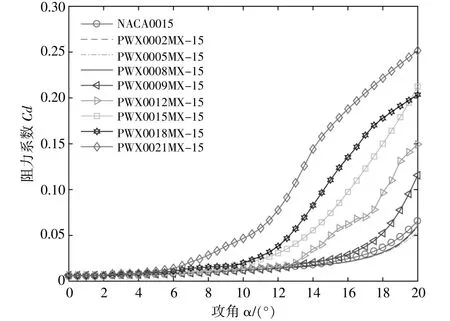
圖7 t/c=15%時，PWX與NACA的阻力系數對比Fig.7 Comparison of resistance coefficient between PWX and NACA at t/c=15%

由圖7可知：當拋物線母線的相對厚度小于9%時，所得到的拋物線翼型等比為t/c=15%時的阻力系數在較小攻角下與NACA0015基本一致；隨著攻角 α的增大，其阻力系數小于NACA0015；當拋物線母線的相對厚度大于9%時，等比后得到的翼型阻力系數小于NACA0015。

圖8為t/c=15%時，PWX與NACA的升阻比對比曲線。

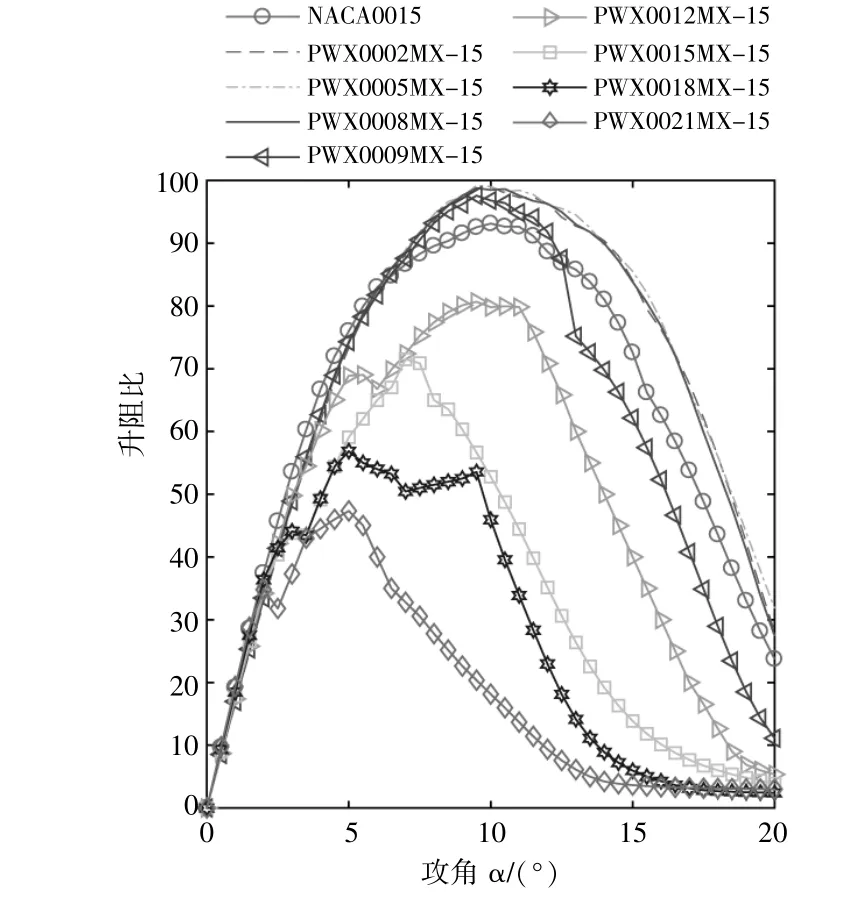
圖8 t/c=15%時，PWX與NACA的升阻比對比Fig.8 Comparison of lift-to-drag ratio between PWX and NACA at t/c=15%

由圖8可知：當拋物線母線的相對厚度小于9%時，所得到的拋物線翼型等比為t/c=15%時的最大升阻比均高于NACA0015，可提高變槳距HVAWT的氣動性能；與NACA0015相比，相對厚度小于9%的拋物線翼型有著較寬的高升阻比范圍，這對定槳距H-VAWT十分有利。

由圖6～8可以看出，當拋物線母線的相對厚度大于9%時，其氣動性能不如NACA0015翼型。這是由于隨著拋物線中常數C值的增大，拋物線母線型線與其所對應的前緣半徑逐漸增大所致。

圖9為PWX翼型母線相對厚度與其前緣半徑間的關系曲線。

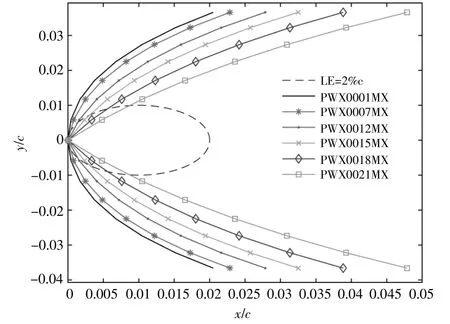
圖9 PWX翼型母線相對厚度與其前緣半徑間的關系Fig.9 The relationship between the relative thickness of the PWX airfoil bus and its leading edge radius

由以上結論可將相對厚度小于9%的拋物線翼型母線等比為t/c=9%，t/c=12%，t/c=18%，t/c=21%的翼型，與相對厚度對應的NACA4系列對稱翼型的氣動特性對比結果如表2，3所示。

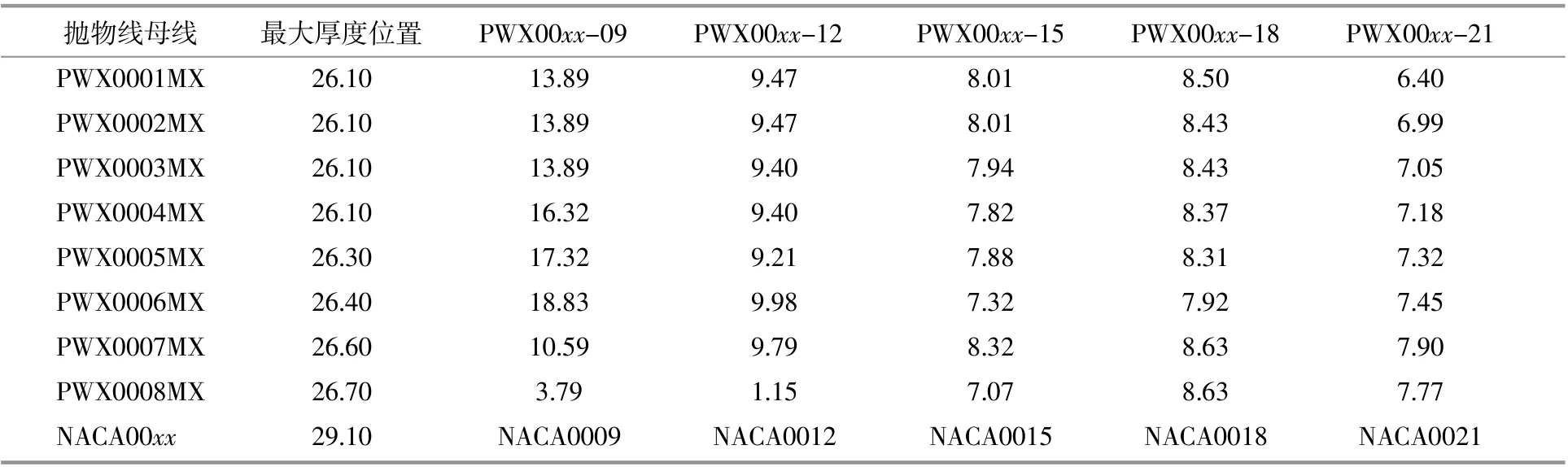
表2 拋物線翼型最大升力系數比NACA4系列對稱翼型提高百分比Table2 The maximum lift coefficient of parabolic airfoil is increased by percentage compared with NACA4 series symmetrical airfoil %

表3 拋物線翼型最大升阻比比NACA4系列對稱翼型提高百分比Table3 The maximum lift-to-drag ratio of the parabolic airfoil is higher than that of the NACA4series symmetrical airfoil%

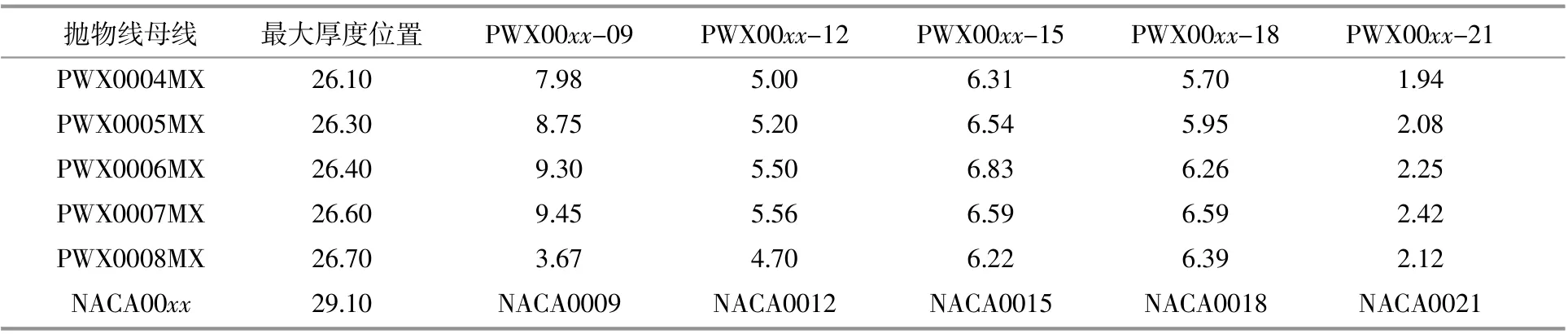
續表3

由表1～3可以看出，當C≥7.74所對應的拋物線母線相對厚度≤8%時，以這些翼型為母線等比后的拋物線翼型氣動性能均優于同等相對厚度的NACA4系列對稱翼型，在薄翼型中表現的尤為明顯。并且在拋物線翼型中，當相對厚度相同時，隨著最大厚度位置越靠近后緣，其翼型的最大升力系數與最大升阻比先增加后減小，在26.6%弦長處所對應的PWX0007MX翼型氣動性能最優。以t/c=15%為例，對最優拋物線PWX0007MXxx系列翼型型線進行對比（圖10）。

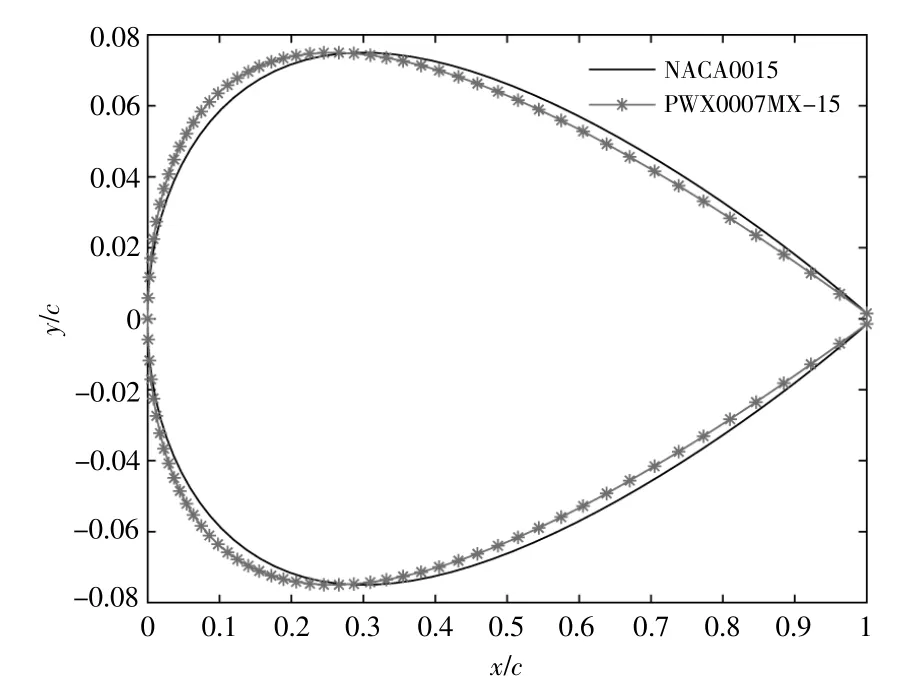
圖10 PWX0007MX-15與NACA0015型線Fig.10 PWX0007MX-15and NACA0015type line

由圖10可以看出，兩種翼型型線在0.27c附近相交，在0～0.25c處，PWX0007MX-15厚度大于NACA0015，在0.27～c處，PWX0007MX-15厚度小于NACA0015。

4 結論

①拋物線翼型中常數C的取值越大，拋物線翼型母線的前緣半徑越大，相對厚度越小，最大厚度位置越靠近前緣；當C≥7.74時，得到的所有拋物線對稱翼型母線等比后均優于NACA4系列對稱翼型，薄翼表現的更明顯。

②當C=10.21時，所得到的PWX0007MX-xx系列翼型最優，其中分別等比為t/c=9%，t/c=12%，t/c=15%，t/c=18%和t/c=21%時，相較于H-VAWT常用NACA00XX系列同厚度翼型，最大升阻比分別 提 高9.45%，5.56%，6.59%，6.59%和2.42%，最大升力系數分別提高10.59%，9.79%，8.32%，8.65%和7.90%。

③相對厚度相等的拋物線翼型，隨著最大厚度位置靠近后緣，其氣動性能先增加后減小，在26.6%弦長處最高；最大厚度位置相同的拋物線翼型隨著相對厚度增加，其氣動性能先增加后減小，在t/c=15%時最高。