2-CPR/UPU三平移并聯(lián)機構(gòu)運動學(xué)分析與優(yōu)化設(shè)計

李麗紅 張發(fā)海 朱 磊

（1 江蘇安全技術(shù)職業(yè)學(xué)院 機械工程學(xué)院， 江蘇 徐州 221000）

（2 中國礦業(yè)大學(xué) 材料與物理學(xué)院， 江蘇 徐州 221116）

0 引言

空間三平移并聯(lián)機器人機構(gòu)具有結(jié)構(gòu)剛度大、控制精度高、承載能力強等優(yōu)點而被廣泛應(yīng)用于工業(yè)包裝、航空航天、3D 打印等領(lǐng)域[1]。Vischer 等[2]最早提出三平移DELTA 機構(gòu)；Tsai等[3]提出一種空間三平移并聯(lián)機構(gòu)，其支鏈由平行四邊形機構(gòu)、移動副構(gòu)成。此外，還有一些學(xué)者研究了通過DELTA 機構(gòu)衍生出的三平移并聯(lián)機構(gòu)[4]。以上機構(gòu)都有耦合度大于等于1 的特點，這也使得機構(gòu)不具有運動解耦特性，直接導(dǎo)致三平移機構(gòu)動力學(xué)分析、運動規(guī)劃與控制分析過程十分復(fù)雜。

目前，解耦空間三平移并聯(lián)機器人機構(gòu)的設(shè)計與研究成為國內(nèi)外學(xué)者關(guān)注和研究的熱點[5]。毛璽等[6]設(shè)計了一種支鏈完全對稱分布且零耦合度的三維純平移并聯(lián)機器人機構(gòu)，并根據(jù)螺旋理論方法對運動輸出特性進行了計算；建立運動學(xué)方程并得到機構(gòu)的位置解、速度、加速度等運動學(xué)分析；通過Matlab 和SolidWorks 聯(lián)合仿真得到樣機的位移、速度、加速度等參數(shù)所對應(yīng)的運動規(guī)律曲線圖；在此基礎(chǔ)上，研究得到位置工作空間及其奇異性特征。季曄[7]設(shè)計了一種弱耦合且無奇異的三平移并聯(lián)機構(gòu)，通過螺旋理論和Kutzbach-Grubler 公式推導(dǎo)驗證了機構(gòu)運動性質(zhì)；建立約束方程并得到運動學(xué)位置方程解析式，根據(jù)雅可比矩陣分析得到機構(gòu)無奇異位置特征；根據(jù)五次多項式對機構(gòu)動平臺參考點進行了軌跡規(guī)劃。程剛等[8]根據(jù)方位特征集拓?fù)浣Y(jié)構(gòu)設(shè)計理論，闡述了并聯(lián)機構(gòu)解耦特性分析過程，提出一種零耦合度的三平移并聯(lián)機構(gòu)；該機構(gòu)具有結(jié)構(gòu)簡單、位置正逆解分析容易等特點，為該并聯(lián)機構(gòu)實現(xiàn)高精度位置控制提供了可能。沈惠平等[9]針對三平移并聯(lián)機構(gòu)運動控制及軌跡規(guī)劃等較為復(fù)雜的問題，提出了一種具有解析式位置正解的三平移并聯(lián)機構(gòu)；計算出方位特征集為三平移、耦合度為0、自由度為3；推導(dǎo)了運動學(xué)方程位置解的符號解析式，分析操作空間和奇異性特征的性能；最后通過仿真分析運動規(guī)律，驗證得到與理論計算一致的結(jié)果。曾達幸等[10]針對三平移并聯(lián)機構(gòu)的綜合問題，通過螺旋理論闡述了移動副存在的條件，利用支鏈輸入副的選擇原則得到支鏈的運動副配置，綜合出全局各向同性的三維移動解耦并聯(lián)機構(gòu)；并對該機構(gòu)進行數(shù)學(xué)建模并完成了運動學(xué)位置分析；建立靈活性的目標(biāo)函數(shù)完成位形優(yōu)化，并進行了樣機研制。朱偉等[11]提出了一種弱耦合且對稱的三平移并聯(lián)機構(gòu)，其中，2條支鏈結(jié)構(gòu)為RRPaR，另外一條支鏈結(jié)構(gòu)為PPaP；計算了幾種重要的拓?fù)浣Y(jié)構(gòu)特征，完成了數(shù)學(xué)方程模型的建立，并得到位置解（正解和逆解）的符號解析式。

考慮到強耦合三平移并聯(lián)機構(gòu)輸出強耦合所引起的實時控制問題，本文中根據(jù)拓?fù)浣Y(jié)構(gòu)綜合理論，提出一種耦合度為0 的新型2CPR/UPU 三平移并聯(lián)機構(gòu)，并對其進行了運動學(xué)分析和參數(shù)優(yōu)化。

1 并聯(lián)機構(gòu)結(jié)構(gòu)分析

1.1 機構(gòu)設(shè)計

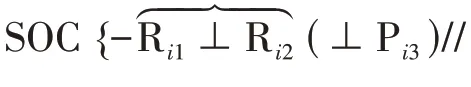
圖1 2CUP-UPU并聯(lián)機構(gòu)結(jié)構(gòu)簡圖Fig.1 Structural diagram of parallel mechanism of 2CUP/UPU

1.2 拓?fù)涮匦苑治?/h3>

并聯(lián)機構(gòu)自由度計算公式根據(jù)方位特征集拓?fù)浣Y(jié)構(gòu)綜合理論進行計算[12]，具體定義為

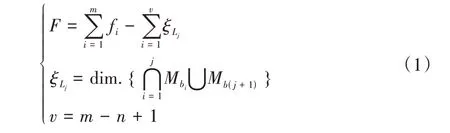
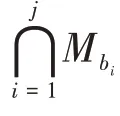
作為衡量并聯(lián)機構(gòu)復(fù)雜程度的耦合度指標(biāo)，基本運動鏈的耦合度κ為

式中，mj為第j個SOCj的運動副數(shù)；Ij為第j個SOCj的驅(qū)動副數(shù)。

圖2 2CPR/UPU并聯(lián)機構(gòu)三維模型Fig.2 3D model of 2CPR/UPU parallel mechanism

（1）根據(jù)機構(gòu)結(jié)構(gòu)簡圖和三維模型圖，根據(jù)支鏈各運動副之間的布置特點，分析出支鏈對應(yīng)的POC集Mbj分別為

式中，Mbj為支鏈j的方位特征集；t為移動特征；r為轉(zhuǎn)動特征。

②支鏈2、支鏈3 的單開鏈為SOC{-Ci⊥Pi2//Ri3}，（i=2，3）計算得到支鏈的Mbj為

（2）分析第一條獨立回路的位移方程，以第2支鏈、第3 支鏈構(gòu)成第一個獨立運動回路，根據(jù)

式（1），則回路1的位移方程ξLj為

①計算第2支鏈、第3支鏈構(gòu)成的子并聯(lián)機構(gòu)的POC集為

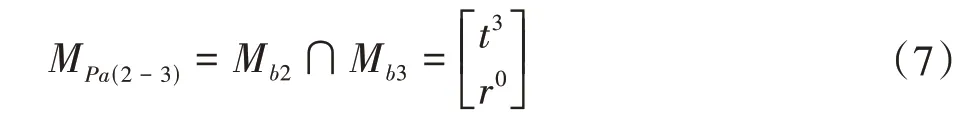
②將參數(shù)代入式（1），得到由支鏈2、支鏈3 組成的子并聯(lián)機構(gòu)的自由度F2-3為

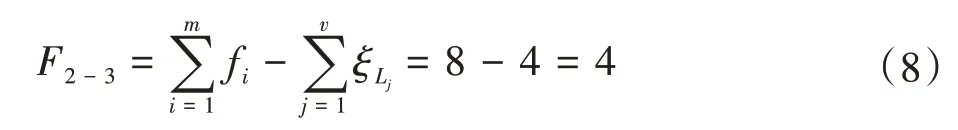
（3）分析第二條獨立回路的位移方程拓?fù)涮匦裕曰芈? 與支鏈1 組成第二回路，將相關(guān)參數(shù)代入式（1），得到回路2的位移方程數(shù)ξL2，有

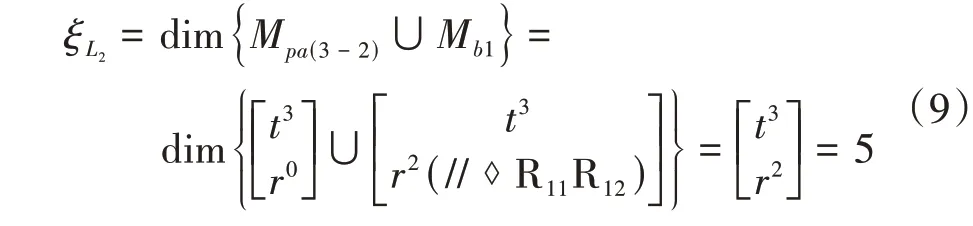
①并聯(lián)機構(gòu)的POC集Mpa(1-2-3)為

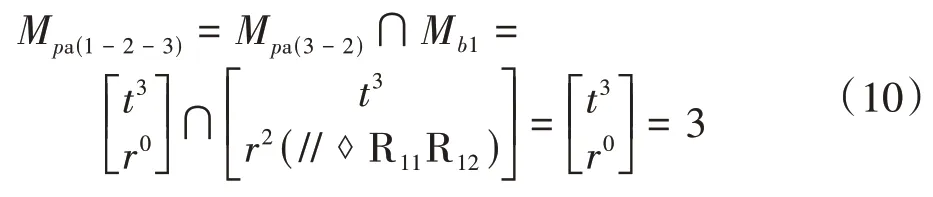
②得出機構(gòu)自由度F1-2-3為

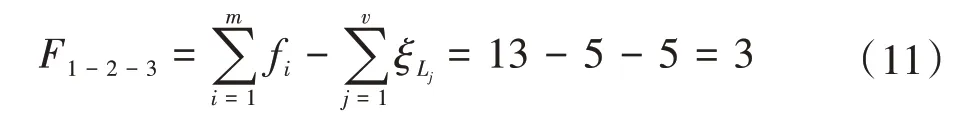
（4）約束度Δj分析，根據(jù)上述步驟代入式（3）中。計算過程為

結(jié)果分析表明，2CPR/UPU 并聯(lián)機構(gòu)具有空間三維移動的運動特性，耦合度k為0，機構(gòu)的運動學(xué)和動力學(xué)分析容易、實時控制精度高；另外，位置正解具有符號解。

2 機構(gòu)的位置分析

2.1 位置逆解分析

機構(gòu)位置逆解分析是指通過動平臺位置輸出得到輸入的表達式的過程[13]。設(shè)定動平臺位置中心P點坐標(biāo)（x，y，z），即為動平臺位置輸出。將靜坐標(biāo)系{O-xyz}建立在靜平臺中心。

已知P點坐標(biāo)（x，y，z），利用平移轉(zhuǎn)換原理映射到Ai點在靜坐標(biāo)下的坐標(biāo)點，即A1（x，y-r，z）、A2（x-r，y，z）、A3（x，y+r，z）。同樣，可得到Ai點在靜坐標(biāo)下的坐標(biāo)點B1（0，-R，0）、B2（-R，0，0）、B3（0，R，0）、M1（R，-R，0）、M2（-R，-R，0）、M3（-R，R，0）、M4（R，R，0）。

根據(jù)移動副的位移恒定為li，建立約束方程為

對于支鏈2、支鏈3 而言，B2和B3的位置不固定，通過向量之間的外積原理，推導(dǎo)得到的關(guān)系等式為

通過等式（13）和等式（14），得到運動約束方程為

分離變量得到逆解表達式為

2.2 位置正解分析

位置正解分析是指已知移動副輸入（l1，l2，l3）推導(dǎo)出動平臺執(zhí)行末端位置（x，y，z）的過程。利用等式（15）推導(dǎo)出運動學(xué)正解符號解析式為

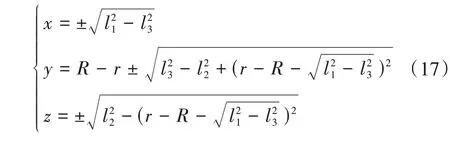
3 奇異分析

3.1 機構(gòu)雅可比矩陣

機 構(gòu) 的 輸 入l=（l1，l2，l3）T，所 對 應(yīng) 的 速 度l?=(l?1，l?2，l?3)T，動 平 臺 執(zhí) 行 末 端 位 移X=（x，y，z）T，執(zhí)行末端速度可表示為=(vx，vy，vz)T。

同時，對等式（15）求導(dǎo)并分離變量，推導(dǎo)出機構(gòu)正逆解雅可比矩陣。

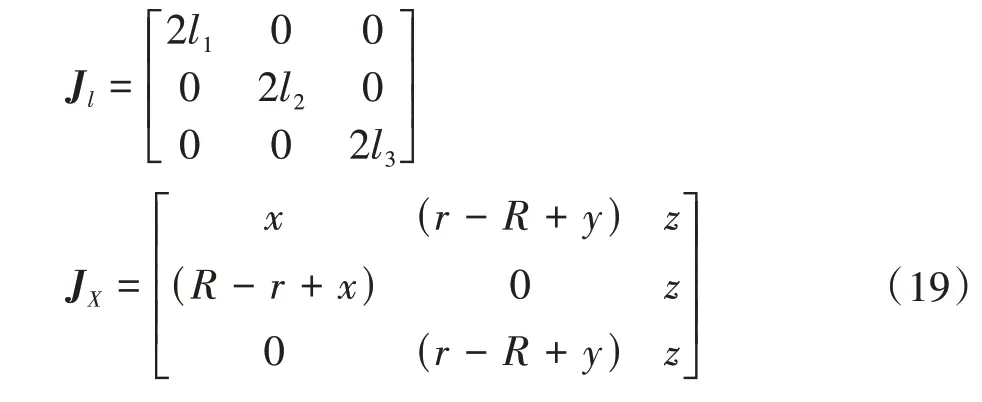
式中，Jl為逆雅可比矩陣；JX為正雅可比矩陣。

若JX非奇異，則

[76]Economic Survey of Burma, 1954, Rangoon: Superintendent, Union Govt Printing and Stationery, 1954, p.10.

若Jl非奇異，則

3.2 逆解奇異性分析

機構(gòu)逆解奇異發(fā)生的條件為det(Jl)= 0 且要求det(JX)≠0。計算得到det(Jl)表達式為

det(Jq)= 8l1l2l3（22）

滿足det(Jl) = 0 的條件有3 種情況，分別是支鏈1、支鏈2、支鏈3驅(qū)動副位移為0，當(dāng)任意支鏈驅(qū)動副位移為0時，機構(gòu)處于臨界位置狀態(tài)，該情況下會處于卡死狀態(tài)。該情況也叫邊界奇異。通過控制驅(qū)動副的移動范圍可有效地解決該極限邊界奇異發(fā)生。圖3所示為逆解奇異。

圖3 逆解奇異情形Fig.3 Singular case of inverse solution

3.3 正解奇異性分析

機構(gòu)正解奇異發(fā)生的條件為det(JX)= 0 且要求det(Jl)≠0。經(jīng)推導(dǎo)計算得到det(JX)的表達式為

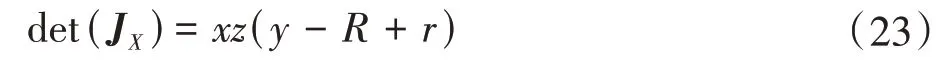
正解奇異出現(xiàn)條件為det(JX)= 0，即存在條件是x= 0或y=R-r或z= 0。

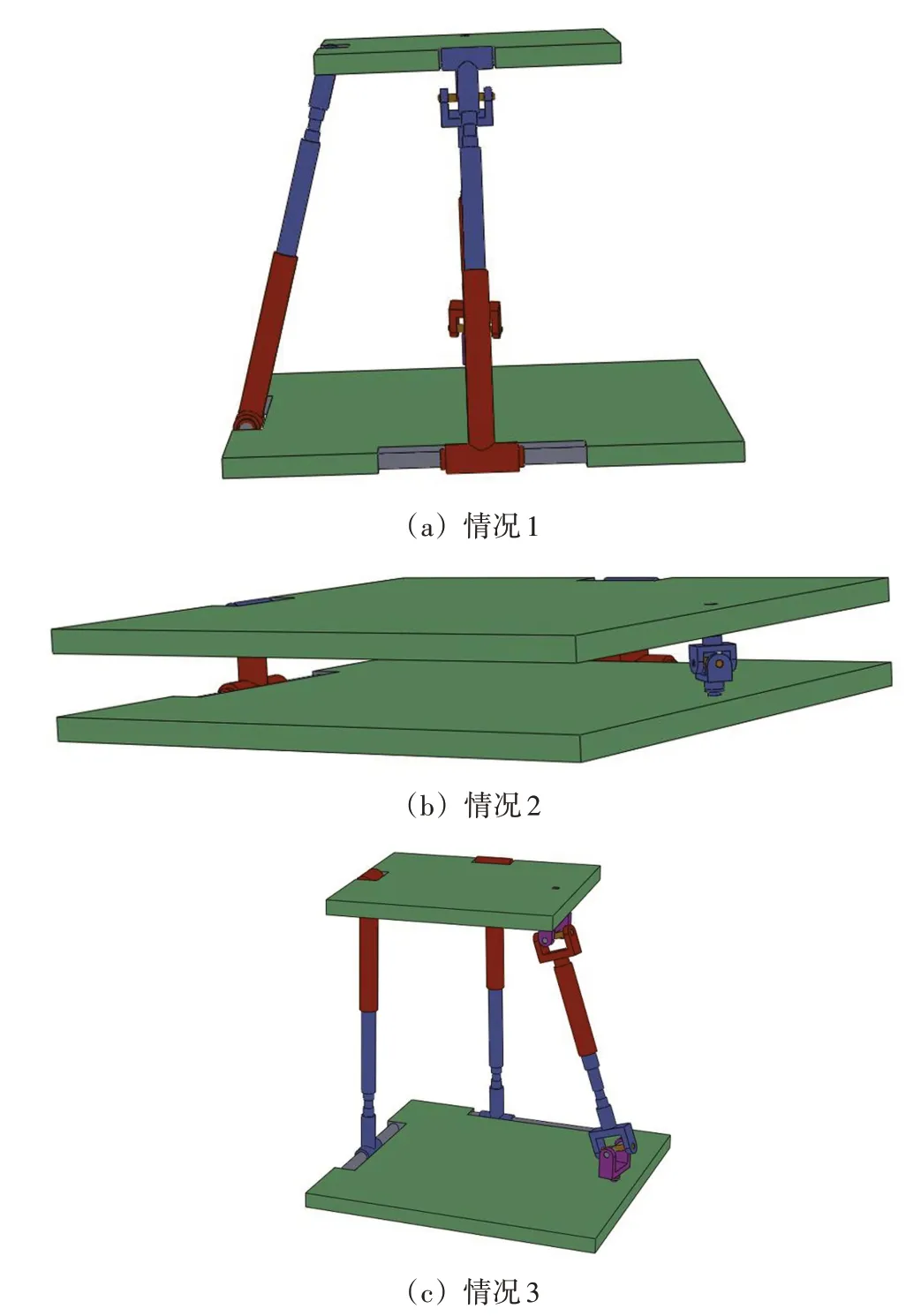
圖4 正解奇異情形Fig.4 Singular case of positive solution

3.4 混合奇異性分析

機構(gòu)混合奇異發(fā)生的條件為det(JX)= 0 且det(Jl)= 0，所有支鏈驅(qū)動副位移為0，則要求動靜平臺尺寸相同，即R=r。因此，混合奇異存在條件為{l1=l2=l3= 0，R=r}。此時，動靜平臺理論上重合才能出現(xiàn)該奇異。該奇異失去自由度，應(yīng)當(dāng)在設(shè)計過程避免出現(xiàn)。混合奇異如圖5所示。

圖5 混合奇異情形Fig.5 Mixed singular case

4 機構(gòu)的工作空間分析

機構(gòu)的運動范圍主要受主動副運動范圍、運動學(xué)逆解、轉(zhuǎn)角干涉等約束條件所限制[14]。在仿真分析并聯(lián)機構(gòu)工作空間的過程中，需要結(jié)合這些約束條件，采用極值搜索法得到工作空間的邊界，邊界點內(nèi)點的集合即搜索得到的工作空間圖形。以表1中的算例參數(shù)值為例。

表1 機構(gòu)的一組參數(shù)值Tab.1 A set of parameter values of the mechanism

由圖6所示可知，工作空間形狀呈半橢圓形，且工作空間邊界位置光滑，并沒有空洞，形狀對稱性較好；在x-o-y投影面關(guān)于y=0 對稱分布，類似“傘狀”分布；在y-o-z投影面完全關(guān)于y=0 對稱分布，呈橢圓形狀分布；在x-o-z投影面，形狀類似橢圓形狀，關(guān)于y=0.1對稱，整個工作空間較大。

圖6 工作空間三維圖Fig.6 3D diagram of the mechanism workspace

5 并聯(lián)機構(gòu)運動靈巧性分析

靈巧度是一種評價并聯(lián)機構(gòu)運動過程中傳遞精度的性能指標(biāo)。靈巧度越高，機構(gòu)的各向同性越好[15]；一般根據(jù)運動學(xué)方程的雅可比矩陣進行計算分析。靈巧度具體定義為

當(dāng)GCI= 0 或者接近0 時，所對應(yīng)的雅可比矩陣為病態(tài)矩陣，機構(gòu)的運動性能較差，輸入輸出之間的傳遞精度低；反之，當(dāng)GCI= 1 或者接近1 時，機構(gòu)的運動性能較好，且對應(yīng)的輸入輸出的傳遞精度高，運動傳遞偏差小。利用上述定義公式，通過Matlab 軟件，根據(jù)圖7所示靈巧度在工作空間內(nèi)的搜索流程，采用極坐標(biāo)搜索法完成整個搜索過程，計算執(zhí)行末端在操作空間內(nèi)的運動靈巧度分布。

圖7 運動靈巧度搜索流程圖Fig.7 Flow chart of motion dexterity search

圖8所示為機構(gòu)在工作空間內(nèi)靈巧度分布以及不同高度下靈巧度分布圖。由圖8中可知，工作空間表面的靈巧度分布均勻，當(dāng)z=0 時，GCI= 0 或者接近0，機構(gòu)的運動性能較差，輸入輸出之間傳遞精度差。z=0.1 m 時，運動性能由外向內(nèi)越來越大，機構(gòu)的傳動精度越來越高，所對應(yīng)的靈巧度在中間區(qū)域最大，最大值為0.75左右。z=0.2 m時，中間區(qū)域的靈巧度略高于邊界區(qū)域的靈巧度，中間區(qū)域的靈巧度最高可達0.4左右。當(dāng)z=0.3 m和z=0.4 m時，靈巧度不隨位置而改變，所有的靈巧度相同，各位置分布均勻，傳遞性能一般，輸入輸出之間傳遞精度不高。

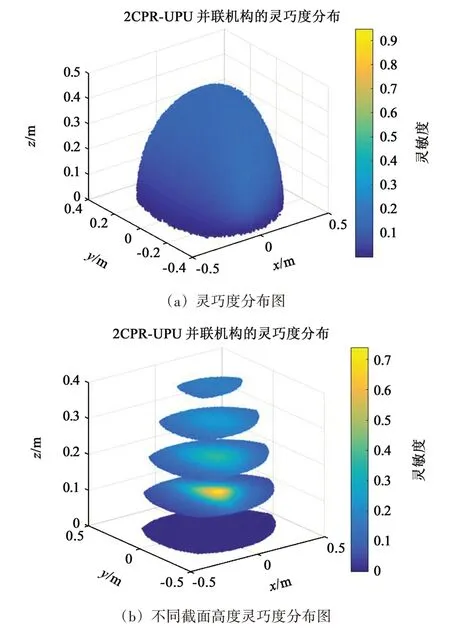
圖8 運動靈巧度分布圖Fig.8 Distribution of movement dexterity

6 尺度綜合

6.1 優(yōu)化模型建立

考慮到實際工程需求，期望獲得更好的運動靈活性性能。可通過優(yōu)化2CPR/UPU并聯(lián)機構(gòu)的幾何設(shè)計變量來解決尺寸綜合問題。建立目標(biāo)函數(shù)以及給定結(jié)構(gòu)參數(shù)約束范圍分別為

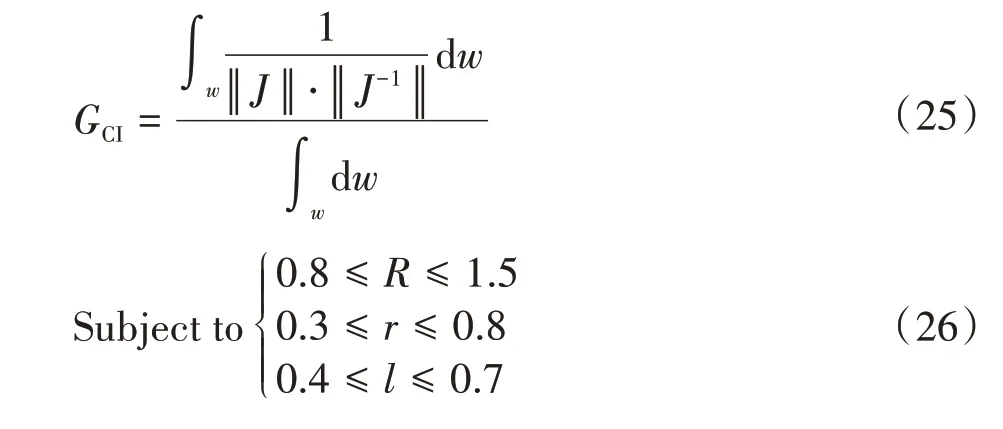
6.2 優(yōu)化算法的選擇

針對上述含有約束變量的單目標(biāo)問題，選擇一種模仿蝗蟲在自然界的群集行為的蝗蟲優(yōu)化算法（Grasshopper optimization algorithm，GOA）[16]對目標(biāo)函數(shù)進行優(yōu)化設(shè)計。在求解未知搜索空間的實際問題時，GOA 算法在迭代過程中可搜索得到精確的全局最優(yōu)值，具有迭代精度高、擴展性強、優(yōu)化效率高的特點[17]。蝗蟲優(yōu)化算法的參數(shù)選取如表2所示。

表2 蝗蟲優(yōu)化算法參數(shù)Tab.2 Parameters of grasshopper optimization algorithm

根據(jù)Matlab 軟件編程得到優(yōu)化目標(biāo)隨迭代次數(shù)的變化圖如圖9 所示。目標(biāo)函數(shù)在迭代次數(shù)為40 左右時趨于穩(wěn)定，并穩(wěn)定在0.374 2 左右。得到優(yōu)化后的尺寸參數(shù)的最優(yōu)值如表3所示。

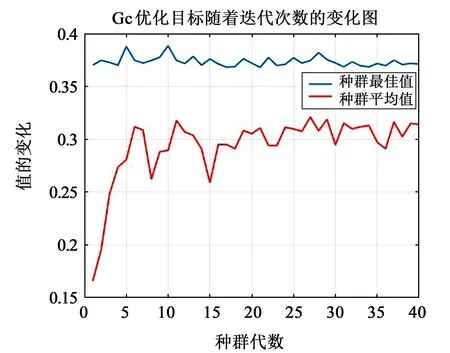
圖9 優(yōu)化目標(biāo)隨迭代次數(shù)變化圖Fig.9 Variation of optimization objectives with iteration times

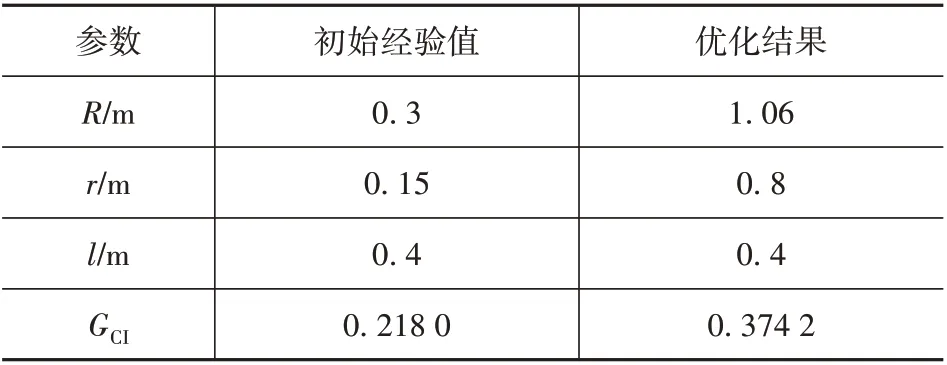
表3 2CUP/UPU并聯(lián)機構(gòu)參數(shù)值對比Tab.3 Comparison of parameter values of 2CUP-UPU parallel mechanism

6.3 優(yōu)化算例分析

利用優(yōu)化后的結(jié)構(gòu)參數(shù)得到的靈巧度分布圖如圖10 所示。和之前的初始經(jīng)驗值相比，優(yōu)化后的靈巧度得到顯著提高，相比之前提升了將近1倍，性能得到大幅提升；優(yōu)化后的機構(gòu)靈巧度分布均勻，邊界表面相比之前得到很大改善，且內(nèi)部的靈巧度最大值最高可達1。此時的機構(gòu)運動過程中，傳遞精度高，運動傳遞偏差小。結(jié)果表明，優(yōu)化后的機構(gòu)性能相對之前更加優(yōu)越；算例分析結(jié)果也說明了算法的有效性和可靠性。

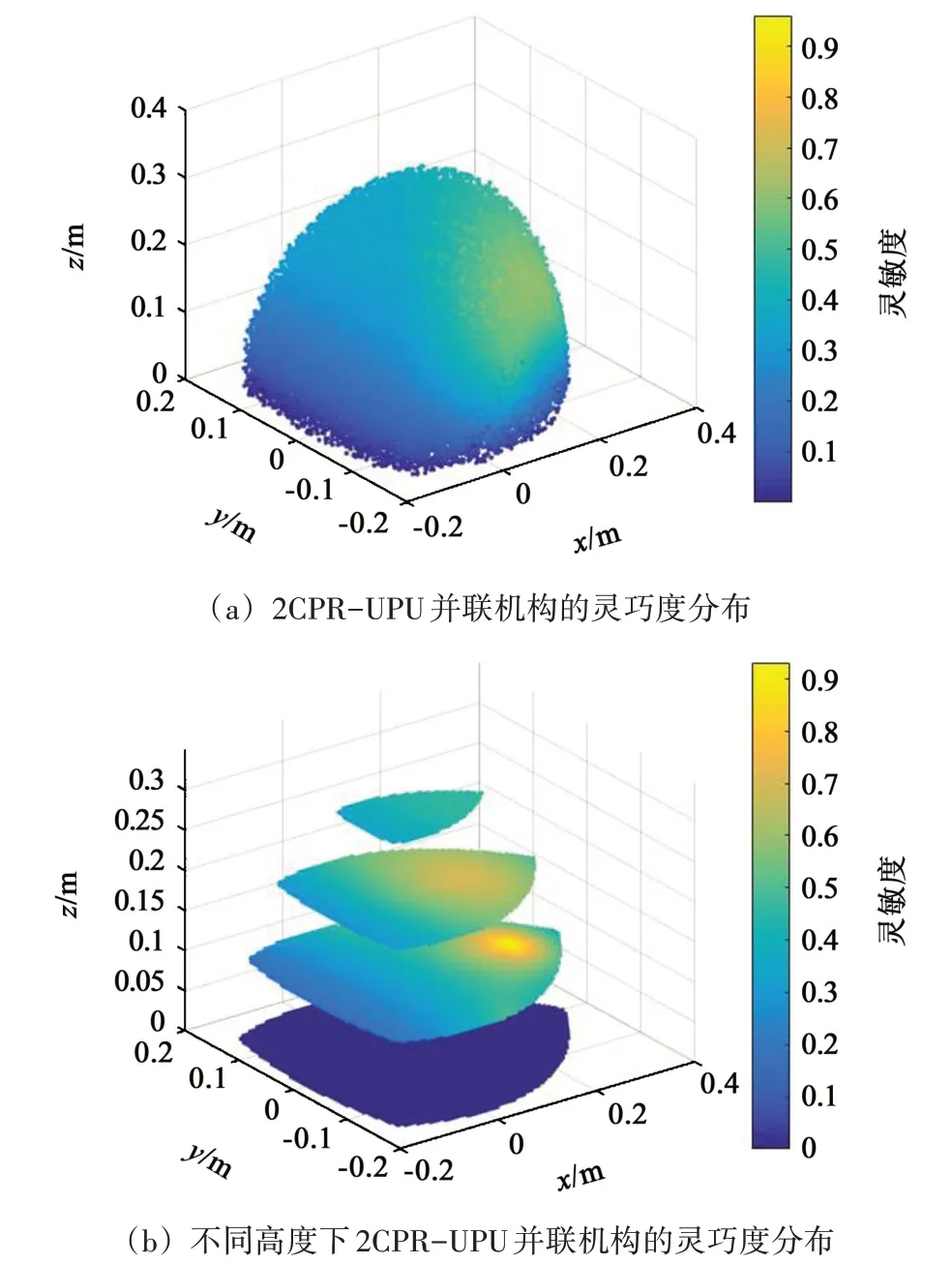
圖10 2CUP/UPU并聯(lián)機構(gòu)優(yōu)化后靈巧度分布圖Fig.10 Distribution of dexterity after optimization of 2CUP-UPU parallel mechanism

7 結(jié)論

（1）設(shè)計了一種弱耦合的空間三平移并聯(lián)機器人機構(gòu)。該機構(gòu)具有輸入輸出實時控制精度高、結(jié)構(gòu)簡單、工作空間大、控制容易等諸多優(yōu)點。

（2）通過建立的運動學(xué)方程模型，研究了奇異性存在條件以及工作空間、靈巧度等性能。結(jié)果表明，機構(gòu)的工作空間性能較大，且邊界光滑無任何空洞的情況；另外，運動靈巧度較好且靈巧度分布均勻。

（3）根據(jù)優(yōu)化仿真模型完成了全局靈巧度的優(yōu)化設(shè)計。最優(yōu)化參數(shù)R、r、l尺寸對應(yīng)的參數(shù)值分別為1.06、0.8、0.4。優(yōu)化后的機構(gòu)全局靈巧度提升約為原來的2倍，較之前運動性能更為優(yōu)越。