解耦機構研究現狀與分析

屈淑維 郭志宏

（1 中北大學 機械工程學院， 山西 太原 030051）

（2 惡劣環境下智能裝備技術山西省重點實驗室， 山西 太原 030051）

0 引言

當今自然界生物體所呈現的聯結方式主要有串聯、并聯及混聯。工程學中，人類所締造的各類機械秉承了自然界萬物的聯結關系，這些聯結關系通過鉸鏈和構件形成了開環或閉環結構；為實現不同的功能需求，又形成了各類串聯、并聯及混聯機構。

串聯機構結構無耦合、控制容易，精度較低，被廣泛應用在工程機械領域。并聯機構結構緊湊、剛度大、承載能力強、累計誤差小、精度高、工作空間小，被廣泛應用于各類精密加工設備中。混聯機構結構龐大、構型復雜，單模塊化功能強，多被應用于大型及巨型裝備的在線加工操作。

由于并聯、混聯機構存在閉環結構，機構控制困難、標定復雜、響應速度慢。而解耦機構可簡化控制與標定，奇異位形少、工作空間大、運行精度高、能耗低，引起了學術界及產業界的廣泛關注，成為機構學的研究熱點之一[1]。

本文中通過研究解耦機構型綜合方法及流程，揭示了解耦機構設計的關鍵技術是通過不同的驅動器實現獨立的位姿輸出；提出了支鏈解耦運動副軸線方向與位置的約束關系；根據支鏈輸出運動特征，分析了驅動副選擇原則；以輸出運動解耦為目標，探討了幾類運動特征轉化的設計方案；結合解耦機構的應用領域，指出了解耦機構的理論研究方向及應用拓展領域。

1 型綜合方法

機構的型綜合是根據輸出運動特征進行設計，得到滿足要求機構的過程。解耦機構是以機構運動與約束的變換邏輯關系為基礎，以輸出運動解耦為目標，通過輸入/輸出間獨立的拓撲結構進行機構構型創新設計的過程。目前主要有4種理論方法。

1.1 線性變換

機構關節空間到輸出運動空間及支鏈運動空間到機構輸出運動空間的映射關系可表示為

式中，[v]=[vx vy vz]為動平臺輸出點H的平移速度矢量；[ω]=[ωx ωy ωz]為點H的轉動速度矢量；[A]為機構正向雅可比矩陣；[B]為逆向雅可比矩陣；q為笛卡爾坐標系中驅動副的輸入速度。

式（1）可由線性變換表示為

式中，[J]=[A]-1[B]為全局雅可比矩陣，表示機構輸入/輸出的變換關系。

全局雅可比矩陣J（J-1）從理論上揭示了機構速度空間的映射關系，反映了機構的輸入/輸出特性。當雅可比矩陣為單位矩陣時，機構為各向同性機構；當雅可比矩陣為對角矩陣時，機構為不耦合機構；當雅可比矩陣為三角矩陣時，機構為解耦機構；否則為一般耦合機構。

Gogu[2]根據雅可比矩陣對各向同性機構、不耦合機構及解耦機構進行了型綜合。基于線性變化理論，Glasunov 等[3-4]根據機構的雅可比矩陣進行了機構優選。雅可比矩陣從機構輸入/輸出映射上揭示了機構的運動特征。

1.2 基于單開鏈的約束綜合法

并聯機構是由動、靜平臺及兩者之間的若干單開鏈（混合單開鏈）支路組成。單開鏈被視為機構的一種結構單元。機構的拓撲結構方位特征（POC）可表示為

式中，Mpa為并聯機構的運動特征；MJi（i=1，2，…，m）表示支鏈的運動特征。

式（3）表明，機構的運動特征是所有支鏈運動特征的交集。

機構的拓撲結構特征由耦合度k表示為

耦合度k揭示了多回路機構運動學與動力學的復雜性，為并聯機構的解耦設計提供了理論依據。沈惠平等[5-6]以此為據進行了并聯機構的位置解耦研究。Jin等[7]依據該方法融合拓撲結構及尺度參數對3自由度并聯機構進行了解耦設計。

1.3 旋量理論

旋量由表達方向和位置的雙矢量構成。通過機構的運動旋量系與約束旋量系，支鏈的運動旋量系與約束旋量系的互易（圖1）與從屬（圖2）關系描述了機構的綜合過程。

圖1 機構旋量間的互易關系Fig.1 Reciprocal relation between mechanism screw

圖2 機構旋量間的從屬關系Fig.2 Affiliation between mechanism screw

將以上互易與從屬關系用集合描述為機構運動旋量與支鏈運動旋量及機構約束旋量與支鏈約束旋量間的關聯關系，建立機構輸出與支鏈輸出特征參數間的相互關系。以機構輸出特征參數為目標依次確定支鏈的運動副配置，其型綜合過程表示為

式中，w、ζ分別為機構輸出自由度的數量和特征；$M、分別為機構及支鏈的運動旋量系；$r、分別為機構及支鏈的約束旋量系。

Qu 等[8]4根據旋量理論進行了并聯解耦機構的型綜合。張彥斌等[9]根據互易旋量理論，以分支的驅動旋量、主動旋量和可動非主動旋量間的相互關系，得到了3自由度各向同性平面并聯機構。

1.4 GF集理論

GF集是機構末端速度特征的一種集合，依據轉動特征與移動特征的拓撲關系，以Plücker 坐標為基礎，描述拓撲結構關系。GF集的型綜合過程可由式（6）～式（7）表示為

式中，GF為末端速度特征，GFi表示第i(i=1，2，…，n)條支鏈的末端速度特征。

式中，FD為機構末端輸出特征；N為支鏈數；n為具有主動驅動的支鏈數；qi為主動支鏈i上的驅動器數；p為被動支鏈數。

GF集的型綜合主要依據移動特征與轉動特征間的影響規律進行拓撲結構綜合。影響規律表現為：①第一類六維全集GF集與任何其他GF集求交時不改變其他GF集的特征。②移動全集與任何其他GF集求交時不改變其他GF集的移動特征。③轉動全集第二類GF與任何其他第二類GF集求交時，如果兩個第二類GF集轉動中心重合，則該轉動全集GF不改變其他集GF的轉動特征。

GF集依據機構移動特征與轉動特征的相互影響及順序性，準確描述了機構末端的運動能力。童幸等[10]基于GF集對3-DOF 解耦（可約）平移機構進行了型綜合。秦友蕾等[11]根據鉸鏈軸線的遷移規律，對3R2T并聯機構進行了解耦綜合。

上述幾種型綜合方法各有特色，為解耦機構的型綜合提供了不同的解決途徑。對上述幾種方法特點的總結如表1所示。

表1 解耦機構型綜合方法的分析Tab.1 Analysis of type synthesis method of decoupled mechanism

類型特點旋量理論GF集理論借助運動旋量系與約束旋量系間的對偶關系及旋量與反旋量間的互易關系。描述型綜合過程。理論描述。依據運動副軸線間的方向與位置約束關系，揭示支鏈的輸出運動規律，探索支鏈間的解耦關系。

上述幾種方法從不同角度為解耦機構的型綜合提供了理論依據。

2 解耦機構的型綜合方法

解耦機構的本質是末端的輸出運動特征能夠通過不同的驅動器控制。當動平臺的部分方位變量只是部分運動輸入變量（θ1，θ2，…，θr）（r＜F）的函數時，機構的輸入/輸出變量間存在一一對應關系，機構完全解耦，表示為

表示三角化結構為

解耦機構的型綜合方法為：根據解耦機構的輸出特征，確定支鏈特征及運動副軸線的方向及位置的約束關系；驗證機構的自由度；輸出特性分析；若滿足解耦輸出特征，則綜合機構為解耦機構，否則重新進行支鏈結構解方位特征配置。具體流程如圖3所示。

圖3 解耦機構的綜合流程Fig.3 Type synthesis procedure of decoupling mechanism

圖3 表明解耦機構設計主要取決于3 個關鍵因素：①機構運動輸出特征與各支鏈末端運動輸出特征的關聯關系（具有可分離自由度）。②支鏈的尺度參數（運動副軸線的幾何及位置約束關系）。③驅動副的選擇。

2.1 機構與支鏈輸出特征關聯關系

根據并聯結構關系，機構部分從動件相對于機架的位置和方向只是部分驅動輸入的函數時，該機構具有部分自由度，表示為

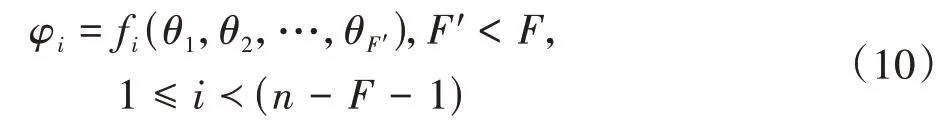
運動鏈拓撲結構關系可表示為

圖4所示為自由度可分離的機構。該機構通過機架分離為兩個獨立運動鏈（SKC），且驅動副位于不同的SKC中，實現驅動與輸出的一一對應。

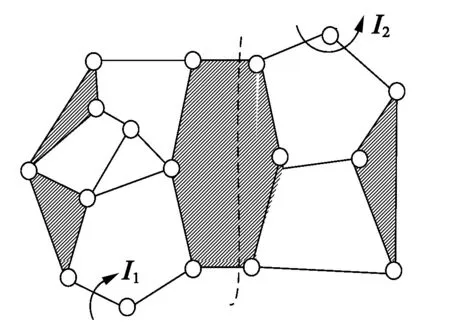
圖4 自由度可分離機構Fig.4 Separable degree of freedom mechanism

2.2 支鏈解耦設計

支鏈解耦設計主要取決于運動副軸線間的約束關系。因此，在滿足驅動副運動特征與支鏈中其他方向運動解耦的條件下，支鏈設計應滿足以下條件：

（1）沿主動副軸線方向上，支路末端構件的輸出必須為該支路主動輸入的函數。

（2）若末端運動特征含有兩個以上移動特征，則支鏈中的轉動副軸線必須正相交或平行；移動副的軸線必須相互垂直。

（3）若動平臺有轉動輸出要求，則所有支路的最后一個運動副應為轉動副，且軸線必須與動平臺轉動輸出軸線的方向一致。

2.3 驅動副的選擇

為了提高機構運行過程中的穩定性，通常所有驅動副位于同一個平臺。對預選的F個運動副為驅動副，將其剛化，得到新機構。需滿足條件為

由于驅動副輸入運動特征往往受軸線遷移的影響，因此，驅動副的選擇應遵循以下原則[8]4：

（1）根據支鏈末端輸出參數的特征要求，依次確定支鏈中運動副類型，且1個支鏈中最多只能含有1個轉動輸入特征。

（2）若支鏈的主動輸入僅含有1個移動特征，則驅動副可為移動副、轉動副或圓柱副；若輸入運動為轉動特征，則驅動副只能為轉動副。

（3）若支鏈主動輸入運動含有兩個移動特征，第1個移動特征的驅動副只能選擇移動副。

3 運動特征的轉化方法

3.1 移動副轉化

沿某一方向的移動副可用與該方向正交的轉動副實現該方向的移動特征，可以改善機構的運動學與動力學性能，易于實現解耦控制。

圖5 所示平行四邊形4R 機構被定義為Pa 運動副。其相對運動存在兩個特點：①構件A與構件B不存在相對轉動。②增加了垂直方向的相對移動。在保持運動輸出不變條件下，用四邊形機構替代P副，能有效改善并聯機構的性能。文獻[12]借助該運動副特性進行了解耦機構的型綜合。

圖5 移動副轉化Fig.5 Prismatic pair transformation

類似特征的平行四邊形機構具有輸出構件相對于機架的姿態保持不變的運動特征，可有效消除機構的轉動自由度，基本類型有4R、4U、4S平行四邊形機構。

3.2 衍生運動設計

衍生運動亦稱伴隨運動。一般情況下，轉動副往往衍生出垂直于其軸線方向的兩個平移運動。如果輸出有平移運動特征要求，則可用轉動副作為驅動副，其衍生運動可實現其他兩個正交方向上移動的輸出解耦。

對于有幾個獨立轉動方向輸出特征要求的機構，衍生運動的消除是設計的難點。在設計中對于僅由轉動副R 組成的單開鏈，每一構件的桿長與軸長皆為0，即所有轉動副軸線交于一點（簡稱恒共點），該結構不存在衍生運動[13-14]，可實現只存在轉動要求的解耦設計，如圖6所示。

圖6 轉動副的恒共點設計Fig.6 Constant common design of rotating pair

Jin 等[15]以此為據，對解耦機構的結構約束特征進行了研究。張帆等[16]借助該結構設計了球面并聯解耦機構。Li等[17]借助該結構對[P]S 類并聯機構進行了無伴隨運動的結構設計。

因此，當支鏈含有兩維或三維共點轉動特征時，轉動中心的位置在移動特征的影響下會發生偏移。如圖7（a）所示，當轉動特征位于支鏈末端，支鏈末端的轉動中心隨支鏈中任一移動特征的變化而變化。此時，機構將喪失全部或部分轉動能力。相反，圖7（b）所示轉動特征不受支鏈中移動特征的影響。因此，當運動鏈末端存在兩維或三維共點轉動特征需求時，應按轉動特征在前、移動特征在后的順序布置。

圖7 混合特征單開聯鏈解耦設計Fig.7 Hybrid characteristic single-open-chain decoupling design

4 解耦機構的應用現狀

隨著機構解耦技術的不斷發展，在工業、航天、醫療和微機械等諸多領域得到了廣泛應用。本節從應用的角度鳥瞰解耦機構的應用研究進展，希望能有更多的學者及工業界人士關注研究解耦機構，進一步拓寬其應用的領域與空間。

4.1 解耦機構與工業

平面解耦操作手可在大工作空間實現位姿的靈活變換，被用于大幅面光電產品的檢測及大型工件的加工操作（加工、焊接、噴涂）[18]。基于連續轉軸的2 自由度轉動機構可用于天線定向、攝像機跟蹤、太陽能定位等2自由度轉動領域[19]。3自由度多軸并聯解耦數控機床樣機為裝備制造業提供了有力的技術支撐[20]。混聯機床運動學的解耦設計，大大提高了控制精度，使工業產品的合格率得到了大幅提高。全解耦3平移多維振動篩可獲得多個工況下物料顆粒的篩分，輸入、輸出具有完全解耦的并聯篩分機構，使茶葉在篩面上快速均布，有效避免茶葉堵塞篩孔，從而提高篩分效率；其振動幅度、頻率和振動自由度都能獨立調節且便于控制，可實現不同品種茶葉的篩分[21]。

4.2 解耦機構與航天工程

航空航天領域中的微器件（微衛星、微陀螺、微加速度計、微傳感器）具有結構尺寸小、精度高等特點。振動性能、可靠性、高靈敏度性能測試是這類微器件測試領域的難題。2 自由度及3 自由度柔性解耦并聯機構，可實現平臺的微定位及精確定位，能夠滿足微器件的測試需求。多維柔性解耦并聯機構則可被應用于加速傳感器的測試實驗[22]。

二維微定位自解耦裝置[23]實現了光刻物鏡檢測平臺的準確定位。全柔性微動全解耦并聯激振臺具有相同的振動規律與振動頻率，容易控制。2自由度轉動解耦的角度調整裝置[24]可用于改變高密度封裝中芯片姿態。彈性整體運動副[25]并聯解耦六維力傳感器無運動副的安裝間隙和偏載、結構簡單、穩定性好、易于制造和安裝。星球探測車通過采用補償鉸鏈解耦法可滿足其在崎嶇地形平穩運行的能力。

4.3 解耦與醫療

近年來，面向生物工程、醫學工程的微操作解耦機器人受到國內外學術界和工程界的廣泛關注，發展速度極快，已被應用于實現細胞的注射分割及微外科手術等。3T2R 并聯解耦機構被用于外科手術的頭部支架[26]。2T2R 機構[27]被用于外科的注射系統。6 自由度解耦并聯機構[28]被用于長骨骨折的回復機構。遠程全解耦并聯機器人被用于外科手術[29]。兩個解耦并聯機構混聯機器人[30]可用于腹腔鏡手術，實現了微創手術操作的技能要求。Kuo 等[31]研發的解耦并聯機構被用于腹腔手術的空間定位機構。

5 發展趨勢

解耦機構的型綜合過程與數學之間存在著不同層次的聯系，數學方法如圖論、集合論、矢量代數、旋量理論、李群、多項式理論、迭代法、同倫法等可直接應用于機構學。

隨著機構解耦技術的發展與成熟，解耦機構已延伸到軍事、生產、生活、康復醫療等諸多領域。解耦設計方法由單一的技術設計向多學科的交叉與融合發展；解耦結構由剛性向剛柔一體化結構發展；應用空間由工農業領域向航天、航空及精密領域延拓。

并聯解耦機構在學術及應用領域引起了極大關注，尤其在解耦措施上，涌現出了多種方法。但目前尚未從理論高度形成系統化的解決方案。解耦機構各種性能指標的定量描述與分析為解耦機構設計及應用提供有效的技術支撐，有利于助推解耦機構向高科技領域延伸。在工農業及日常生活服務領域，將具有解耦特性的并聯機構承載于機器人系統，也將產生巨大的應用空間。

6 結論

（1）支鏈的解耦設計有待從數學理論高度構建統一的生成原理。按照支鏈幾何約束與位置約束建立智能化的生成機理。尤其是根據轉動副軸線的幾何關系、轉動副與移動副對末端特征影響的規律，建立根據輸出運動特征進行逆向求解，獲得解耦支鏈的生成機理。

（2）解耦設計的實現方法體現了學科的交叉與融合。根據機構的不同功能，解耦設計方法出現了“多元化”趨勢。因此，融合其他學科如仿生學、概念創新設計，將為解耦構型提供更多的原生構態。

（3）并聯解耦機構已被廣泛應用于工業、醫療、航天等領域。可以預見，隨著解耦技術的發展與成熟，將進一步擴大其應用領域。同時，將其搭載于機器人系統，將進一步拓寬其應用的空間。