不同孔道形狀對DPF再生性能的影響研究

盧志美，覃神全，李艷勤，黎華揚

（廣西玉柴動力股份有限公司，廣西 玉林 537005）

0 引言

柴油機微粒捕集器（DPF）作為降低PM最有效的后處理裝置之一，憑借其簡單高效的工作特性被廣泛應用于交通運輸、工程機械、農業機械、發電等領域[1]。

DPF在顆粒過濾期間，過濾效率高達90%以上[2]，甚至在形成煙灰層后能達到100%[3]。但由于DPF孔道內的容積有限，顆粒沉積過多將導致排氣壓降升高，不利于發動機正常工作，因此必須以定期燃燒的方式去除顆粒物實現DPF再生[4]。但在DPF再生過程中碳煙顆粒燃燒會產生局部高溫，容易損壞DPF的孔道結構，需要對其孔道結構進行合理的優化設計。

目前，已經有許多學者研究了孔道結構對DPF工作特性的影響。Nakamura等[5]將載體通道由標準正方形幾何體變為正弦波形的通道時。結果表明，增大過濾面積能夠降低其背壓。Ingram等[6]設計了非對稱通道結構的DPF，將入口通孔增大，出口保持不變。研究發現：同樣顆粒存儲量的情況下，非對稱DPF的壓降僅是標準DPF的一半。Segawa等[7]研究發現六邊形非對稱通道過濾器具有較大的開放通道面積，并且其壓降低于方形對稱通道過濾器。

目前對DPF孔道結構的研究主要集中在顆粒捕集階段方面，而模擬不同形狀孔道比對主動再生過程中的再生性能的研究鮮有報道。因此，采用三維模型研究了不同形狀孔道結構對其主動再生過程中溫度場、壓降和再生效率的變化規律，對DPF再生過程中的結構優化設計具有重要的參考意義。

1 數學模型

1.1 氣相控制方程

質量守恒方程：

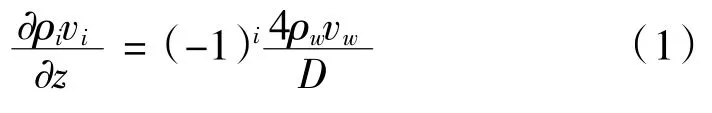
動量守恒方程：

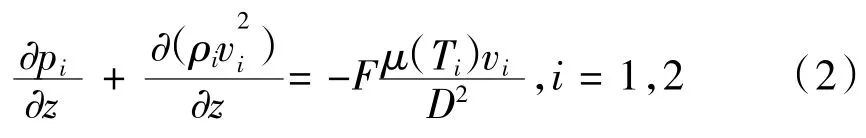
能量守恒方程：

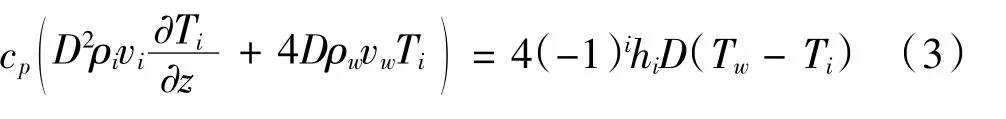
式中：i為氣體通道，i=1為進氣道，i=2排氣道；w為壁面厚度；ρ為氣流密度；v為通道的氣體流速；z為通道中的軸向方向；p為氣體壓力；F為方形通道內的壓降系數，取值為28.45 Pa；μ為排氣的動力黏度；T為內氣流的混合溫度；cp為氣體的比熱容，hi為過濾體孔道氣流與過濾體壁面之間的對流換熱系數。

1.2 固相控制方程

質量守恒方程：

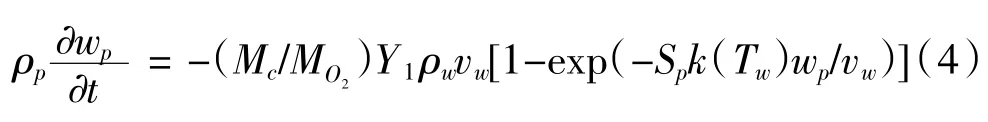
能量守恒方程：

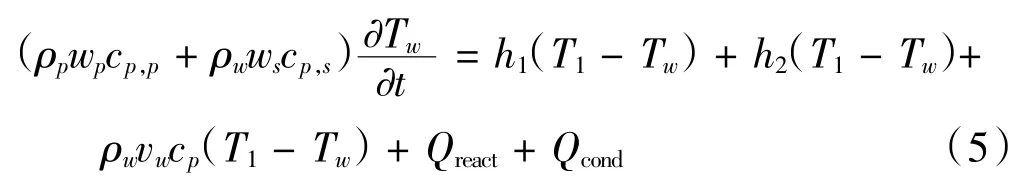
式中：ρp為顆粒層密度，wp為顆粒層厚度；Mc表示碳的分子量；MO2表示氧氣的分子量；Y1為進口通道的氧氣濃度；Sp為被捕集的微粒層的比面積；cp，p是顆粒層的比熱；ws為過濾壁厚；cp，s是過濾器壁的比熱容。

燃燒熱Qreact滿足方程：

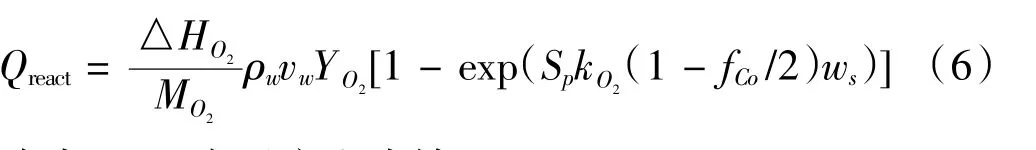
式中△HO2為反應生成焓。

對流熱傳導Qcond滿足方程：

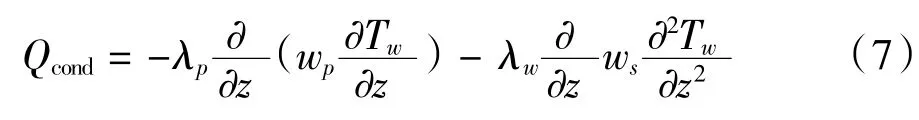
式中，λp為顆粒層的導熱率；λw為過濾層的導熱率。

氧氣組分在壁面上滿足平衡方程：

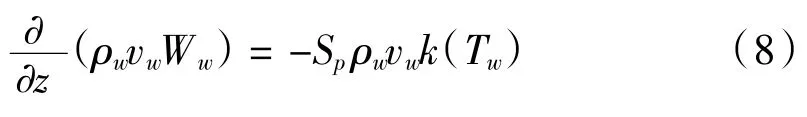
式中，Ww為壁中的含氧量。

1.3 壓降控制方程

氣流經過DPF載體產生壓降損失，過濾壁面和顆粒層被視為兩個相連的多孔介質層，壓降損失遵從達西定律，即

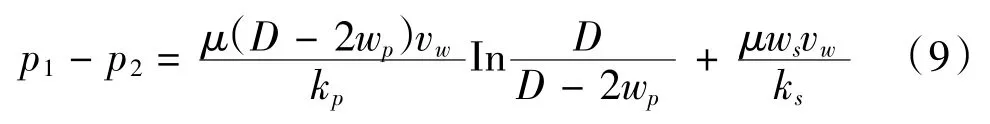
式中，kp和ks分別為顆粒層和壁面的滲透率。

1.4 反應機理

DPF的主動再生通過直接提高進氣溫度使碳微粒與氧氣發生氧化反應，主要化學反應機理如下：

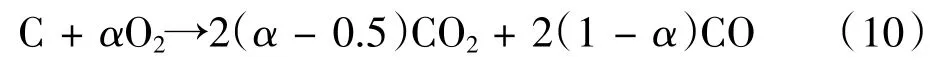
在等式（10），α為碳顆粒氧化反應的完全系數，一般為0.55～0.90。碳粒子氧化反應的焓ΔH可以表示如下

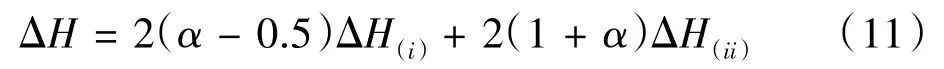
其中ΔH（i）和ΔH（ii）分別是CO2和CO的形成焓，J/mol。

1.5 孔道結構

標準的DPF孔道是方形的壁流式結構。為了研究不同孔道結構對DPF再生性能的影響，提出了兩種用于過濾器的不同通道結構，。3種孔道結構分別為正方形、六邊形和八邊形，如圖1所示。

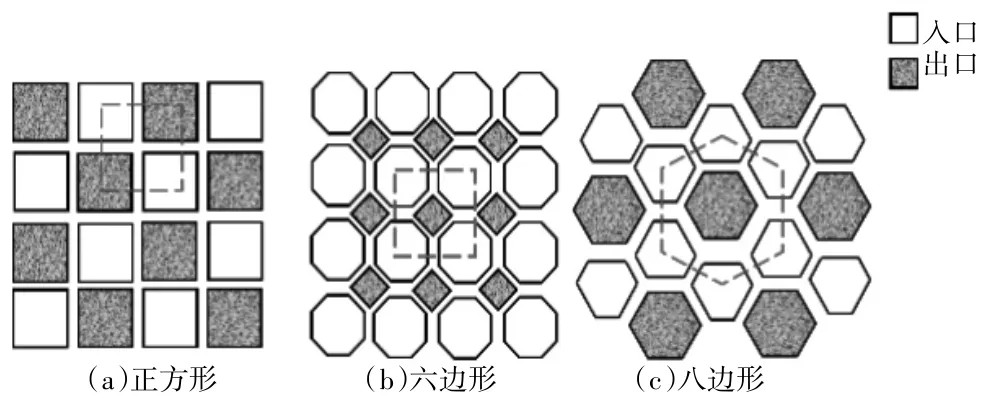
圖1 DPF的不同通道形狀

2 物理和數學模型

DPF主要由進氣管路、濾芯和出氣管路三部分組成。本研究采用壁流式碳化硅DPF，具體的結構參數見表1。采用AVL-FIRE軟件進行模擬計算，進氣道和出氣道的網格設置為5 mm，燃燒區域的網格為3 mm。DPF的計算網格如圖2所示。

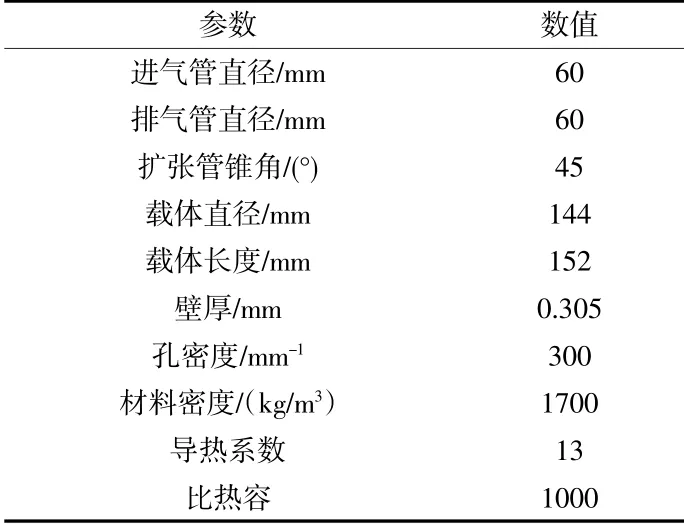
表1 DPF結構參數

圖2 DPF計算網格

3 模型驗證

為了驗證上述數值計算模型的準確性，對DPF再生過程進行了大量的建模和數值模擬研究，本研究得到的模擬結果與Mayari的試驗數據進行了驗證[8]。其中，模型驗證計算過程所需的排氣狀態參數和過濾器結構參數與文獻中的參數保持一致。模型求解參數見表2。圖3顯示了在DPF中心軸上三個位置的壁溫測量結果和數值模擬結果的比較。顯然，由該圖可以看出當前研究的模擬結果和文獻中的試驗結果之間有良好的一致性，且誤差較小，驗證了模型的準確性和可靠性。

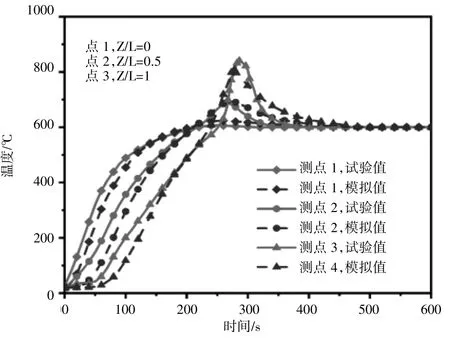
圖3 模型驗證

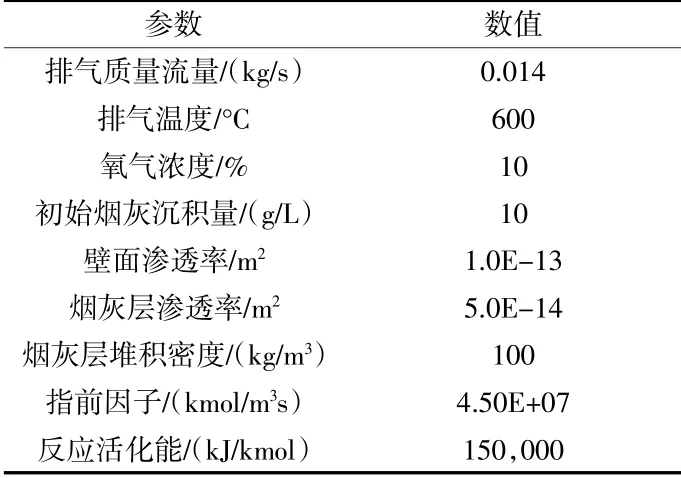
表2 模型求解參數

4 結果與分析

4.1 不同孔結構對溫度場的影響

在不改變DPF過濾體其他參數的情況下，改變過濾體的孔道結構，研究其對再生過程的影響。根據八邊形通道的DPF在145 s時候達到峰值溫度，壁面峰值溫度為1164.82 K（圖4）。六邊形結構在190 s的時候達到峰值溫度，為1097.45 K。而方形孔道峰值溫度在200 s的時候達到1084.53 K的峰值溫度。3種孔道結構中，正方形結構峰值溫度出現的時間點最晚，峰值溫度也最小。這是因為八邊形孔道的入口通道與出口通道相比來說，入口通道的密度大于出口通道，就導致每個入口通道中的煙灰分布較為均勻，燃燒得更充分，產生的熱量更高且更集中，且加上密度較少的出口通道不利于熱量排出，就容易導致峰值溫度出現得更快且更高。

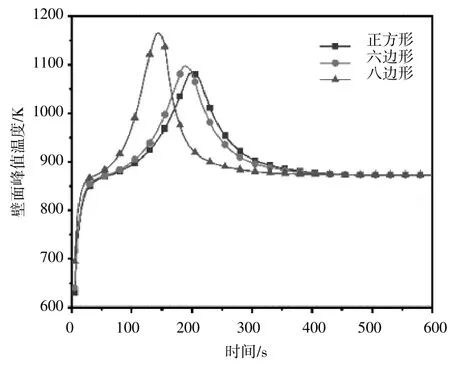
圖4 不同孔結構對再生峰值溫度的影響

4.2 不同孔結構對壓降的影響

DPF再生過程中不同孔結構對壓降的影響如圖5所示。可以看出，雖然初始的煙灰顆粒容量是一樣的，但由于微粒在DPF孔道中的分布不同，導致初始的壓降也不一樣。其中，八邊形孔道的初始壓降最高，正方形孔道的次之，六邊形孔道的初始壓降最低。這是因為微粒在入口處的微粒較少，對氣流的流動阻力較少，故壓降最小。隨著DPF的再生，由于溫度升高導致氣體膨脹，加速微粒無規則運動，碰撞幾率變大，氣體黏度增加，導致流動阻力增大，從而使壓降升高。其中八邊形孔道的煙灰顆粒所產生的壓降最高，這是因為即使在相同的顆粒容量下，均勻分布的微粒所能容納的微粒也是最多的，再生燃燒過程中所產生的溫度也就越高，從而導致更大的壓差。

圖5 手動控制界面

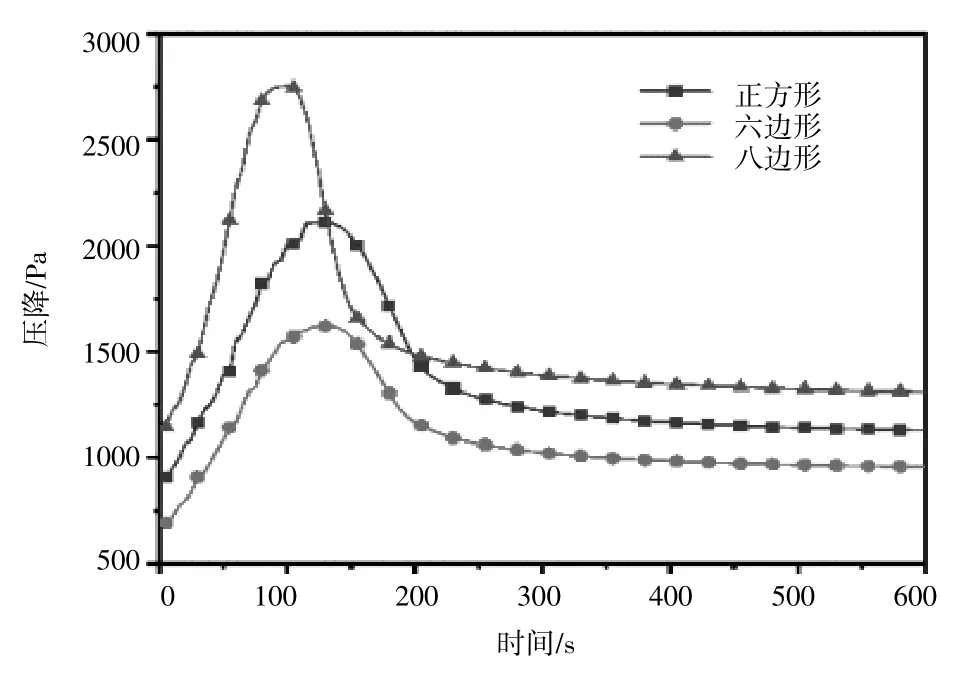
圖5 不同孔結構對再生壓降的影響

4.3 不同孔結構對再生速率的影響

圖6為不同形狀的進出孔道DPF的碳載量隨時間的變化關系。由圖可知，在未達到再生溫度初期，碳載量保持不變。當達到再生溫度后，八邊形孔道DPF的碳載量首先開始下降，且下降趨勢最為迅速。六邊形的下降趨勢次之，正方形的最慢。再生結束后，八邊形DPF載體內殘留的碳煙質量更小。這是因為過濾體直徑和通道密度不變時，八邊形孔道使得進氣孔道表面碳煙層面積增大，與排氣接觸面積增加。在再生過程中，由于八邊形孔道DPF熱量排出較慢，排氣與載體壁面的熱交換更多，使得再生速度較快，總體的再生效率也有所增大。

5 結語

綜上分析，得出以下結論：

（1）DPF再生過程中的壓降呈現先升高后下降的變化趨勢，且再生后壓降大于初始壓降。

（2）八邊形孔道DPF和六邊形孔道DPF再生過程中會產生較高的峰值溫度，但八邊形孔道具有最快的再生速率，六邊形孔道所產生的壓降最小。