雙慣量伺服系統控制參數對伺服動剛度影響

文小滿，鄧火生，丁可，吳錫鵬

（1.廣西機電職業技術學院，廣西 南寧 530007；2.廣西大學，廣西 南寧 530004）

0 引言

隨著交流伺服系統的普及，對伺服系統的控制性能要求也隨之提高。在高速高精的運動控制場合下，伺服動剛度是影響伺服系統穩定性、動態響應能力、抗干擾能力和保證加工精度的關鍵因素[1]。通常將階躍負載力幅值與位置偏差的穩態值的比值定義為伺服靜剛度，而負載力幅值與位置偏差的最大值的比值定義為伺服動剛度[2]。因此，研究伺服參數對伺服動剛度的影響，對提升伺服動剛度以及伺服性能具有重要意義。Alberto等通過模態試驗，測量出關節模態頻率和轉動慣量，以此計算伺服動剛度，并提出一種基于性能指標的姿態優化方法，以提高機械加工中機器人的動剛度[3]。付睿云等人建立經編橫移機構的剛度表達式，通過仿真分析位置增益、速度增益和速度環積分常數對伺服剛度和系統性能的影響，但未考慮傳動機構的剛度[4]。

為了分析伺服參數對雙慣量伺服系統伺服動剛度的影響，提高系統伺服動剛度，通過建立雙慣量伺服系統傳遞函數，推導出伺服動剛度表達式，通過仿真實驗分析伺服參數對伺服動剛度的影響，進而可有針對性地進行參數整定，從而提高系統的抗干擾性能。

1 雙慣量伺服動剛度模型與分析

伺服動剛度是指在動態載荷下，伺服系統抵抗位置偏差的能力。因此，伺服動剛度的表達式為：

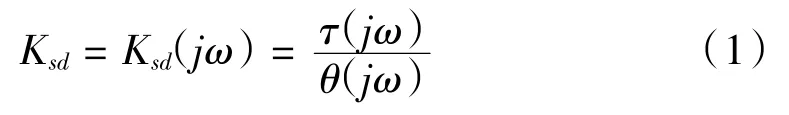
式中，ω表示動態載荷的交變頻率，τ（jω）表示為動態干擾載荷，θ（jω）表示為受到動態干擾載荷伺服系統所發生的變形量。

因Ksd（jω）為復數，故用其幅值衡量伺服動剛度大小，即：

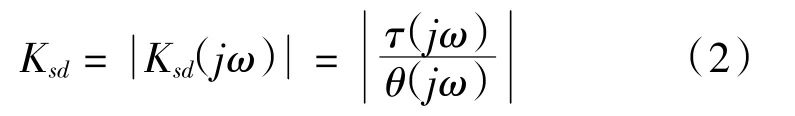
為了建立伺服動剛度模型，首先建立雙慣量傳動模型（圖1）。其中，JM、JL分別為電機和負載的慣量；Ks為傳動機構的剛度系數；N為減速器減速比；TM、TL和TW分別為電機輸出轉矩、負載轉矩和轉動軸扭轉轉矩；bM、bL和bs分別為電機、負載和傳動機構的阻尼系數；θM、ωM、θL和ωL分別為電機和負載的角度和角速度。

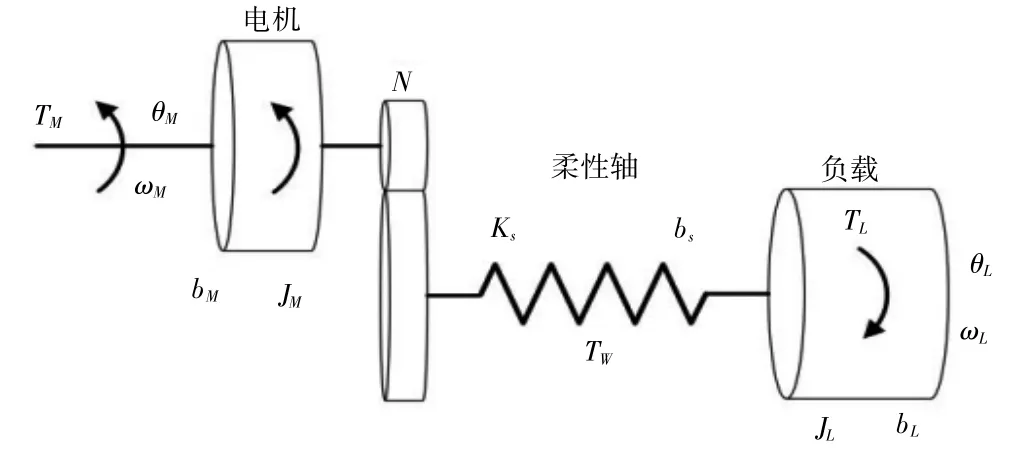
圖1 雙慣量傳動模型

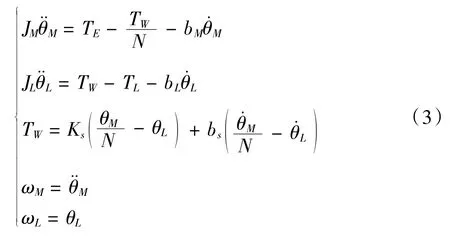
由于系統中的阻尼系數很小，可將其忽略[5]。然后對系統微分方程組進行拉普拉斯變換得：

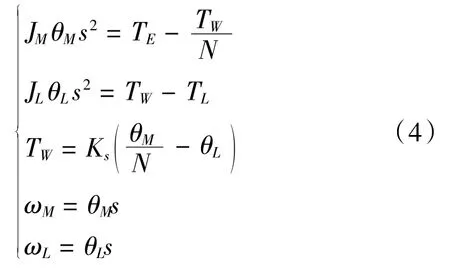
由式（4）可得雙慣量系統框圖（圖2）。

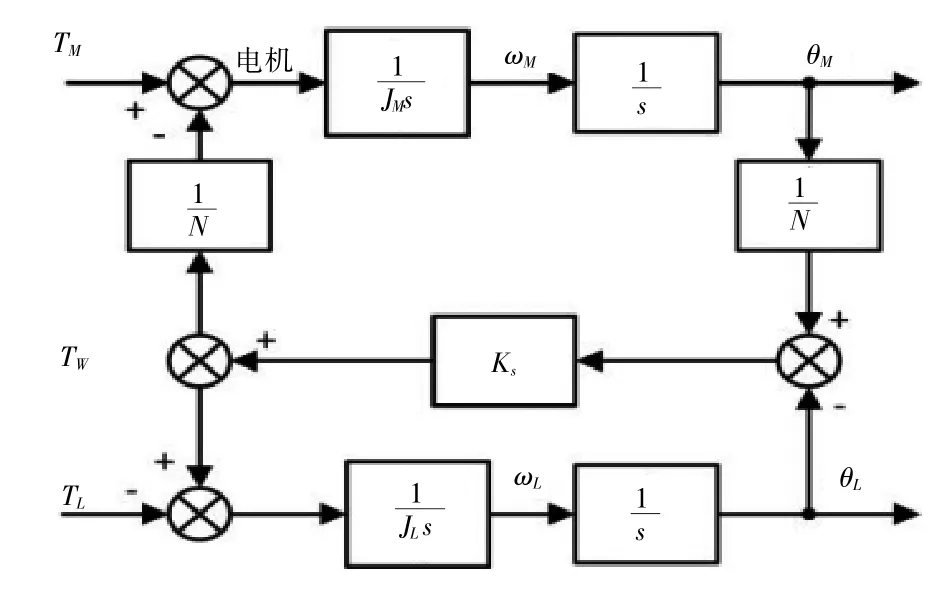
圖2 雙慣量系統框圖

通過雙慣量系統框圖可以得到電磁轉矩TM與電機角速度ωM之間的傳遞函數為：

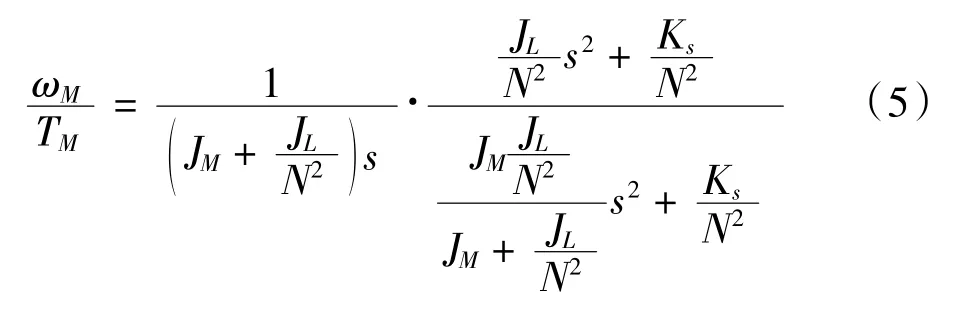
結合伺服驅動控制框圖，可以建立雙慣量伺服系統控制模型（圖3）。其中Kpp表示為位置環比例增益，Kvp和Tvi為速度環比例增益和積分時間參數，Kip為電流環比例增益，Tii為電流環積分時間，TL為負載力和擾動力。最后可以得到單個關機伺服系統整體輸出的θ（s）為：

圖3 雙慣量伺服系統控制模型

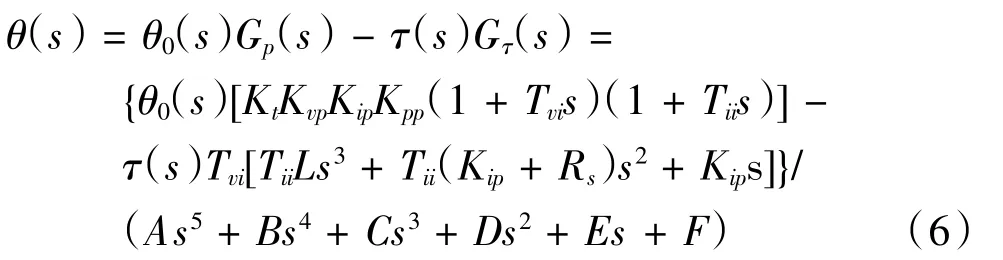
其中：

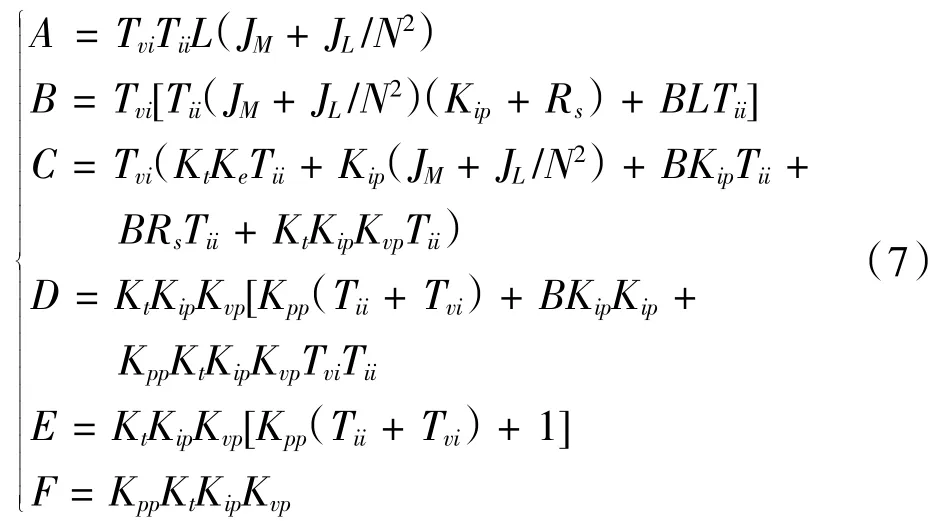
根據伺服動剛度定義可知，伺服動剛度是負載擾動TL作為系統輸入，電機轉子位置θM作為系統的輸出，將位置輸入信號當做為零處理。因此伺服動剛度的函數表達式為：

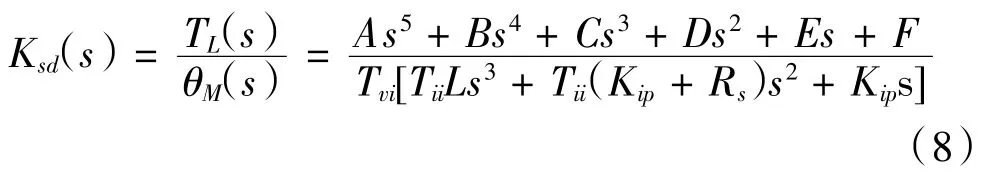
推導出的伺服動剛度表達式可看出，影響伺服動剛度的主要伺服參數有位置環比例增益Kpp，速度環比例增益Kvp，電流環比例增益Kip，速度環積分時間常數Tvi，電流環積分時間常數Tii，系統轉動慣量J等。為簡化分析過程只考慮位置增益Kpp，速度增益Kvp和速度環積分時間常數Tvi對伺服動剛度的影響。

2 伺服動剛度分析

2.1 伺服參數對伺服動剛度影響

為了更加直觀地分析伺服參數對伺服動剛度的影響，結合上一節推導出的伺服動剛度函數表達式，改變位置增益Kpp，速度增益Kvp和速度環積分時間常數Tvi，通過Matlab仿真繪制伯德圖，分析對伺服參數對伺服動剛度的影響。其中伺服系統相關參數具體數值見表1。

表1 系統參數

采用控制變量法，在保證其他的伺服參數不進行修改的前提下，依次修改位置比例增益參數Kpp、速度比例增益參數Kvp和速度積分時間常數Tvi，用伯德圖分析不同伺服益參數對伺服動剛度的影響。

（1）在保證只修改位置比例增益參數，其他的伺服參數不進行修改的前提下，將位置環比例增益參數從5開始，以20為步長，一直增加至105，繪制出位置增益變化時的伺服系統伯德圖（圖4）。通過圖4可以看出隨著位置環比例增益Kpp的增大，伺服系統在2×102Hz處頻段的幅值不斷減小，在此之后的頻率，其伺服系統的幅值不再隨著位置環比例增益Kpp的變化而發生不同的變換，而是變化趨于一致。與此同時，也說明在中低頻內的擾動情況下，伺服系統抵抗干擾的能力隨著位置環比例增益Kpp的增大而增強，而且在干擾頻率越低時，其伺服系統的抗干擾能力就越強。并且隨著位置環比例增益Kpp的增大，系統的幅值下降程度也逐漸放緩。

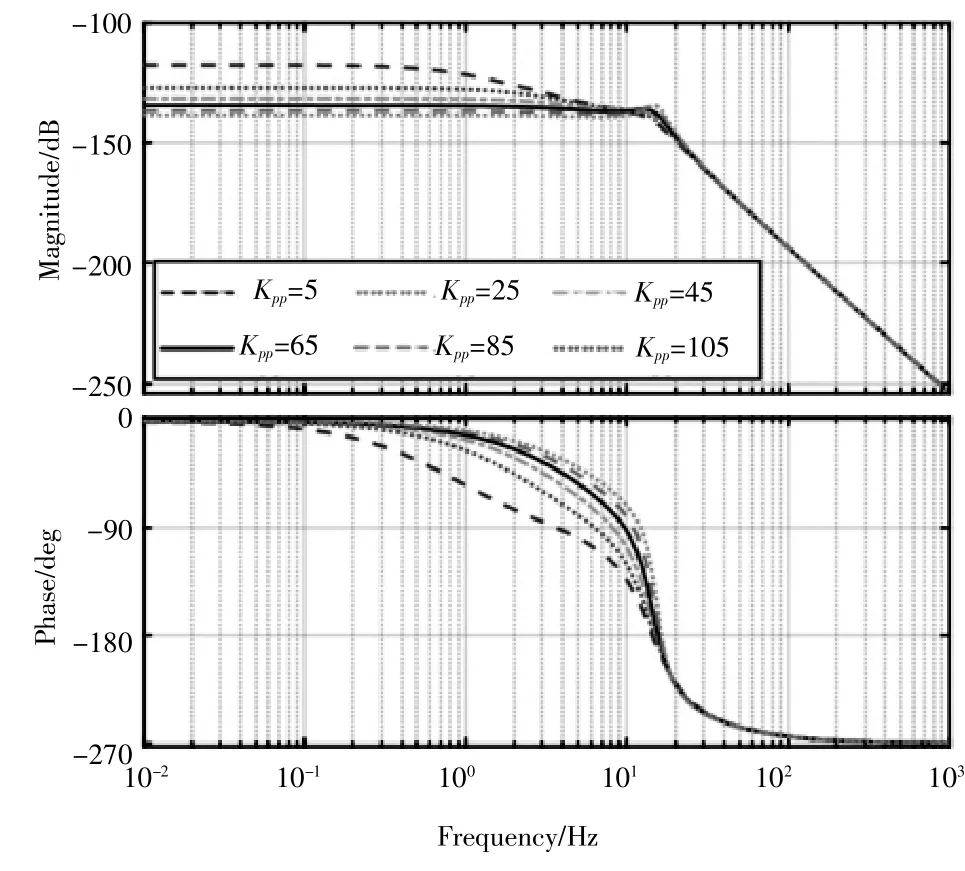
圖4 位置環比例增益變化時伺服系統伯德圖

（2）將速度環比例增益參數從10開始，以10為步長，一直增加至60，繪制出如圖5的伺服動剛度伯德圖。隨著速度環比例增益Kvp的增大，伺服系統在2×102Hz處頻段的幅值不斷減小，在此之后的頻率，其伺服系統的幅值不在隨著速度環比例增益Kvp的變化而發生不同的變換，而是變化趨于一致。與此同時，也說明在中低頻內的擾動情況下，伺服系統抵抗干擾的能力隨著速度環比例增益Kvp的增大而增強，而且在干擾頻率越低時，其伺服系統的抗干擾能力就越強。隨著速度環比例增益Kvp的增大，系統的幅值下降程度也逐漸放緩。

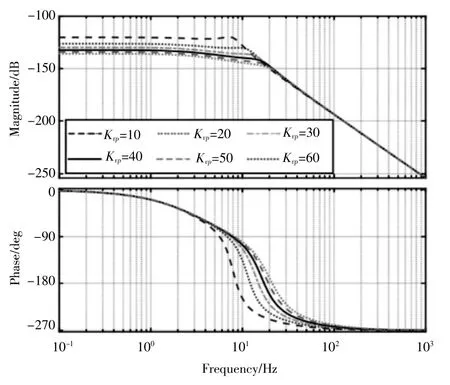
圖5 速度環比例增益變化時伺服系統伯德圖

（3）將速度環積分時間常數從0.1開始，以0.1為步長，一直增加至0.6，繪制出伺服動剛度伯德圖，如圖6所示。隨著速度環積分時間常數Tvi的增大，伺服系統在低頻頻段的幅值不斷增大，在其他段的頻率，其伺服系統的幅值不在隨著速度環積分時間常數Tvi的變化而發生不同的變換，而是變化趨于一致。說明在低頻內的擾動情況下，伺服系統抵抗干擾的能力隨著速度環積分時間常數Tvi的增大而減弱，而且在干擾頻率越低時，其伺服系統的抗干擾能力就越差。并且隨著速度環積分時間常數Tvi的增大，系統的幅值增大程度也逐漸放緩。

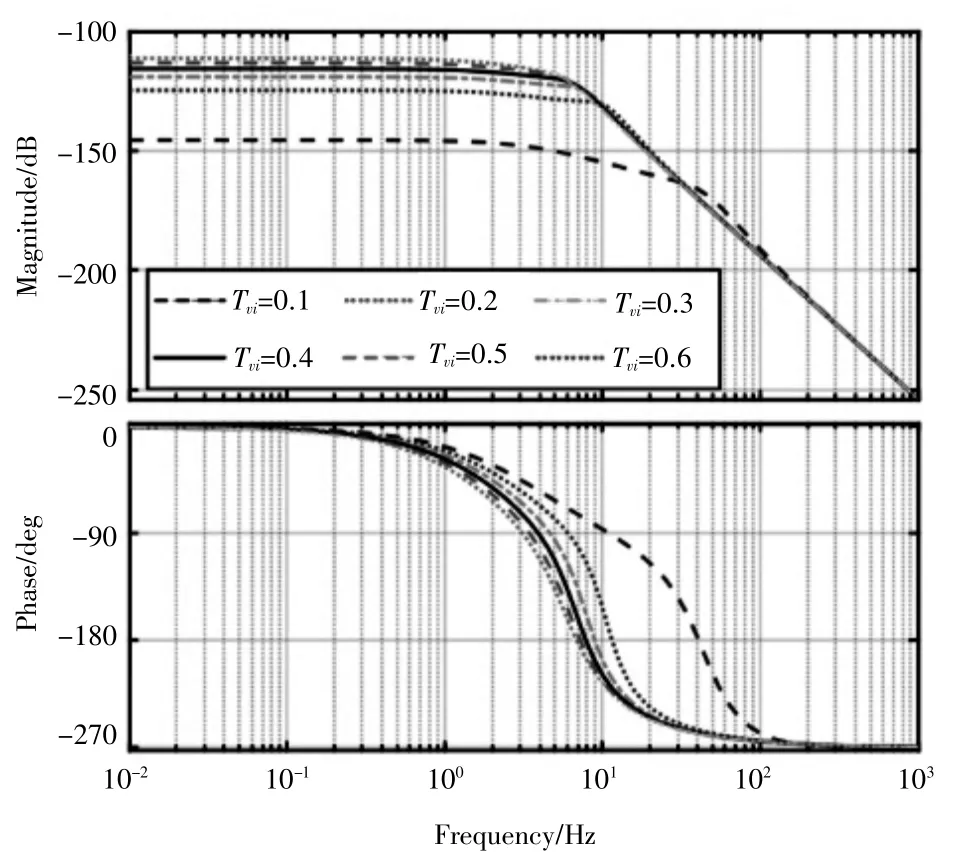
圖6 速度環積分時間常數變化時伺服系統伯德圖

3 結語

為了獲得控制系統參數對伺服動剛度的影響，提高雙慣量伺服控制系統的抗干擾能力，通過建立雙慣量伺服系統控制模型，推導出伺服系統動剛度表達式。使用Matlab軟件對雙慣量伺服系統控制模型進行仿真，仿真結果表明對于中低頻率的擾動，可以通過適當提高位置增益、速度增益和降低速度積分時間常數的方法來提高伺服動剛度，以此增強伺服系統的抗干擾能力，并為伺服動剛度的測量實驗和伺服參數整定提供研究基礎。