彈塑性問題的改進無單元Galerkin方法計算軟件開發
張明哲,彭妙娟,程玉民
(上海大學 力學與工程科學學院,上海 200444)
0 引 言
在求解高速碰撞、動態裂紋擴展和材料幾何非線性等問題時,無網格方法可以基于一系列離散的節點構造試函數,從根本上避免采用有限元法容易發生的網格畸變、計算過程終止等缺點。無網格方法受到越來越多國內外學者的關注,因此開發一款以開放式語言為基礎的無網格方法計算軟件很有必要。
有關彈塑性問題的無網格方法軟件開發起步較晚,現階段比較完善且運用廣泛的工程分析軟件仍然是有限元法軟件,如MSC Nastran、Abaqus、Ansys、MIDAS等。Nayroles等基于移動最小二乘法提出擴散單元法,無網格方法才真正發展起來。王宇新等開發無網格MPM法三維前處理系統;張征等開發接觸力學自適應無網格計算系統,求解二維彈塑性接觸力學;ABBASZADEH等開發一種無網格數值程序模擬地下水污染方程;曾清紅利用并行計算技術進行適于無網格方法的并行插值算法研究;NAKATA等提出一種在圖形處理單元上的基于徑向點插值方法的無網格分析并行算法;SINGH等基于Fortran語言開發并行算法,實現傳熱和流體流動問題的無單元Galerkin方法的并行求解;LIU等使用MLS為無網格方法開發一種基于背景網格的自適應程序;文建波等開發基于Delaunay三角化的無網格方法計算結果后處理軟件。此外,Ansys作為成熟的有限元軟件,已經內置無網格計算方法的模塊。
關于彈塑性問題的無網格方法的研究,傳統無網格方法采用移動最小二乘法構造試函數,在計算過程中容易形成病態或者奇異方程組,而彈塑性問題的求解要求布置足夠多數量的節點以提高計算精度,這嚴重影響計算效率和精度。為解決這些問題并擴大無網格方法的應用范圍,CHEN等應用復變量重構核粒子法,用一維基函數形成二維問題的校正函數解決二維彈塑性問題;CHENG等使用可直接施加邊界條件的插值移動最小二乘法獲得形函數,提出插值無單元Galerkin方法解決二維彈塑性問題;CHENG等采用罰函數法應用本質邊界條件解決二維彈塑性問題,獲得更高的計算精度和效率;MENG等利用維數分裂法將三維波動方程分解為二維問題,推導改進的插值維數分裂無單元Galerkin方法求解三維波動方程;蔡小杰等采用移動最小二乘法建立彈塑性大變形問題的改進的無單元Galerkin方法;DENG等基于改進的復變量無單元Galerkin方法提出二維非線性的彈塑性問題的數值模型;WU等、PENG等和ZHENG等提出改進的無單元Galerkin方法解決彈塑性大變形問題,利用Galerkin積分弱形式建立求解方程,其形函數滿足Kronecker函數的性質,可直接施加本質邊界條件,并提出采用插值無單元Galerkin方法求解三維彈塑性問題,可極大地提高計算效率和精度,由其編寫的無網格方法部分程序算法,可極大地減少計算量。
上述關于彈塑性問題的無網格方法的程序大多不具有全流程分析(精確的計算運行程序和可視化的前、后處理程序),如MATLAB專注于計算程序,使得分析問題時不能在一個軟件中兼顧建模、計算分析和結果展示,也間接阻礙彈塑性問題無網格方法的普及和應用。無網格方法的相關軟件很少有關于彈塑性分析的。
本文開發彈塑性問題的改進無單元Galerkin方法軟件,包括前處理程序模塊、計算程序模塊和后處理程序模塊3個部分。前處理程序鏈接Gmsh建模,可以獲得節點信息等信息流,然后通過彈塑性問題的改進無單元Galerkin方法計算程序進行數值模擬,最后利用后處理程序模塊實現數值結果的可視化。
1 軟件架構
該軟件基于C++編程語言開發,依托改進的無單元Galerkin方法解決彈塑性問題,能夠高效直觀地建模并進行準確的受力分析。軟件面向的對象包括節點、單元以及邊界條件等模型數據,對其進行計算分析后得到處理結果,最后將結果在軟件上以可視化界面進行顯示,即前處理程序、分析計算程序和后處理程序3個部分。前處理程序、計算程序和后處理程序不是互相獨立工作的,其數據聯系流程見圖1。
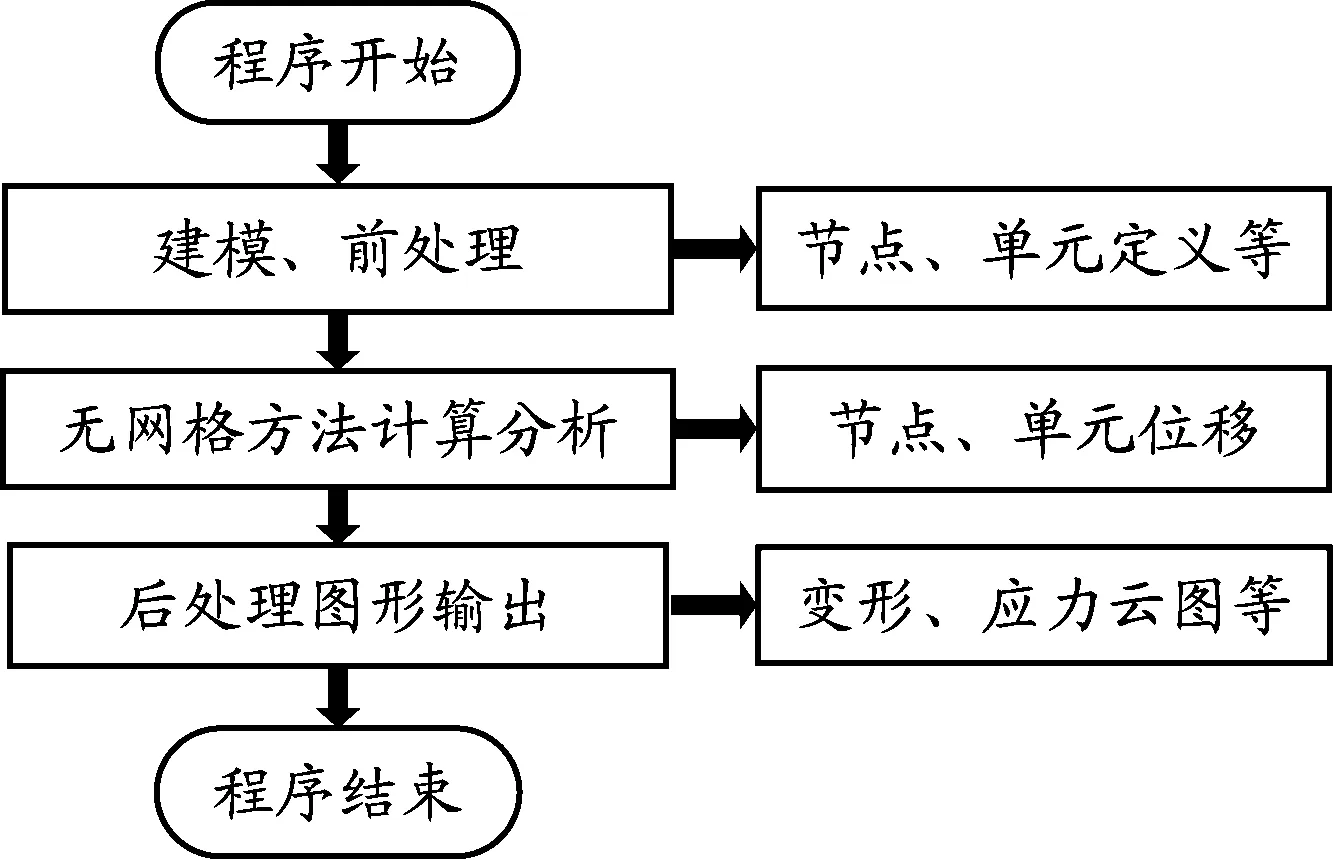
圖1 軟件流程圖
前處理程序模塊主要為建立模型和節點生成:基于OpenGL庫直接使用C++語言進行建模,輸入參數,預處理必備的結構參數值。因無網格方法需要節點進行函數擬合,其中的關鍵環節是對計算域離散剖分并獲取節點信息。無網格方法將計算域離散為一系列點,根據邊界法向前推進,在計算域內部進行填充式布點,同時利用Delaunay算法進行網格篩選以獲得節點信息。無網格方法分析計算部分首先根據建模的維度選擇二維彈塑性或三維彈塑性問題的改進無單元Galerkin方法的程序,將計算得到的數據傳遞給后處理模塊,后處理模塊主要顯示結果。
前處理程序模塊需要輸入模型的幾何信息和物理信息,包括各種屬性和邊界參數等,建立分析模型后對模型進行節點處理。前處理的重點是得到節點信息并讀入模型節點數據,為無網格方法分析做準備。
本軟件鏈接簡單的CAD引擎,通過編程先設定模型所需的主要節點,連點成線,然后生成面,最后生成體。每個點、線、面和體都有唯一的標簽。程序可直接輸入各種幾何信息和物理信息,提供所需的各種屬性和邊界參數,如載荷大小以及坐標、邊界條件等。
計算程序模塊進行無網格方法的計算,最主要的是矩陣計算和求解。
后處理程序模塊對每個單元建立單元節點位移向量。以文件形式讀入前處理獲得的節點幾何信息和網格信息等,將計算程序得到的位移輸入到后處理的坐標修正程序,通過改變節點和網格的坐標值顯示模型的變形量,從而實現模型變形的可視化。
2 前后處理程序模塊
2.1 前處理程序
前處理是數值計算中非常重要的環節,不僅決定著程序解決問題的通用性,而且直接影響后續數值計算的精度和效率。前處理過程首要的是布置節點,包括節點編號及相應的坐標值。節點數據的空間位置信息定義為類P_Point,其C++程序如下。
class P_Point
{
public:
P_Point(const double x = 0,const double y = 0,
const double z = 0):_x(x),_y(y),_z(z) { }
~P_Point() { }
const double get X() const { return _x;}
const double get Y() const { return _y;}
const double get Z() const { return _z;}
void set X(const double x) { _x = x;}
void set Y(const double y) { _y = y;}
void set Z(const double z) { _z = z;}
bool operator <(const P_Point&p) const;
protected:
double *Point_p;
double _x,_y,_z;};
節點數據的獲取采用coord的vector容器接收。節點的初始三維空間信息存儲在vector容器中,每3個連續數據為1組。為方便使用,按照節點排布順序重新存儲數據,其coord的C++程序如下。
std::vector
P_Point p;
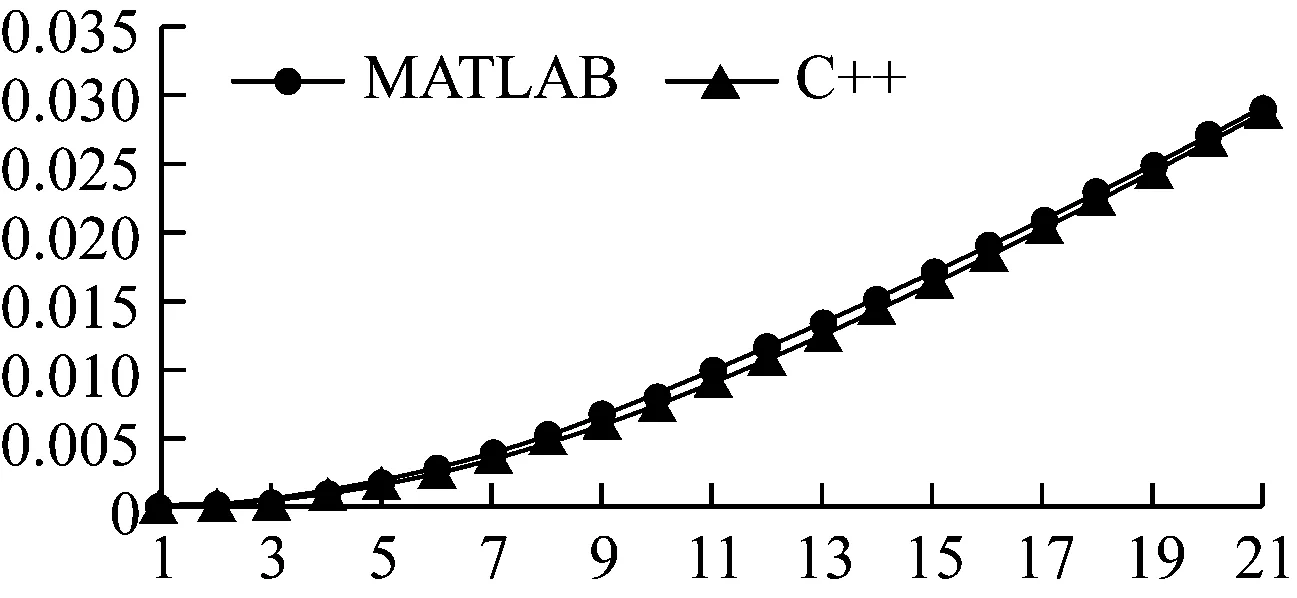
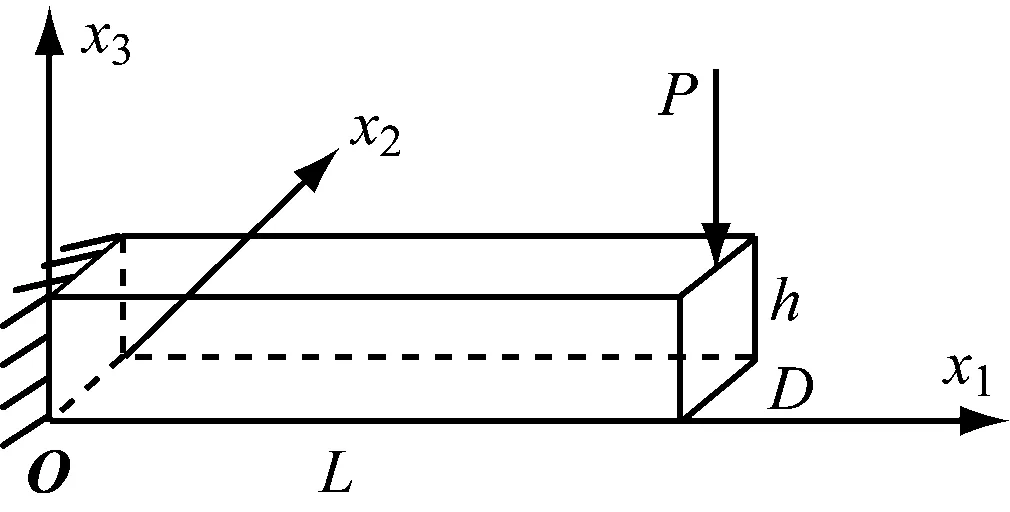
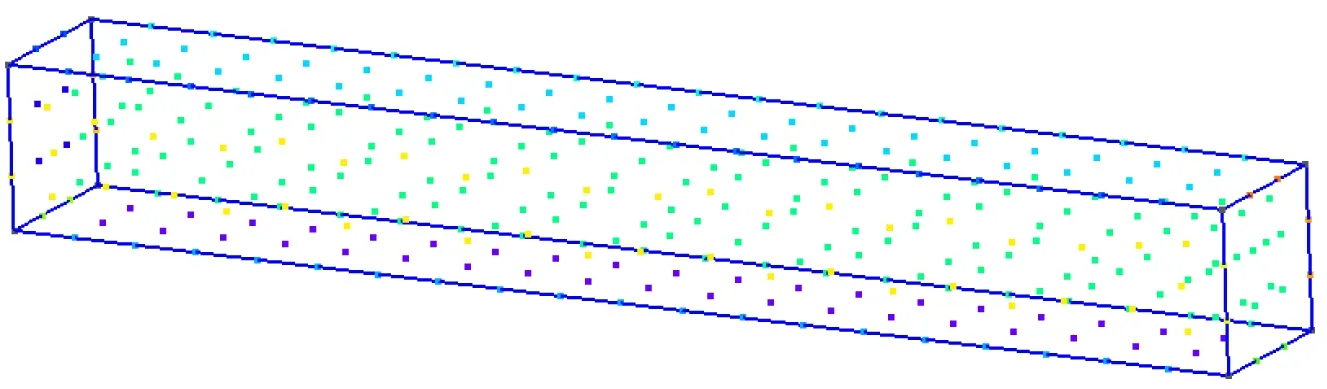
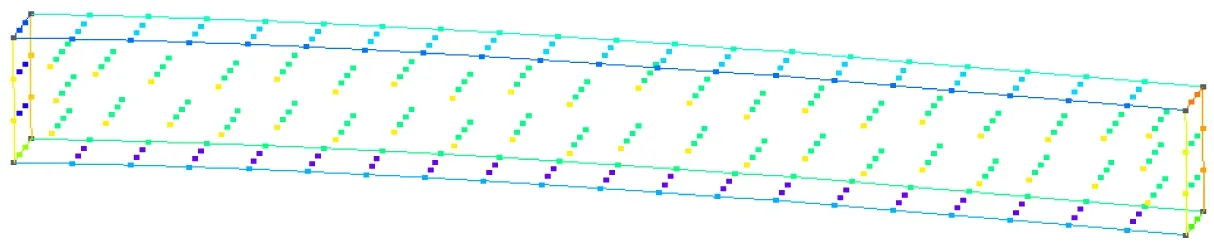
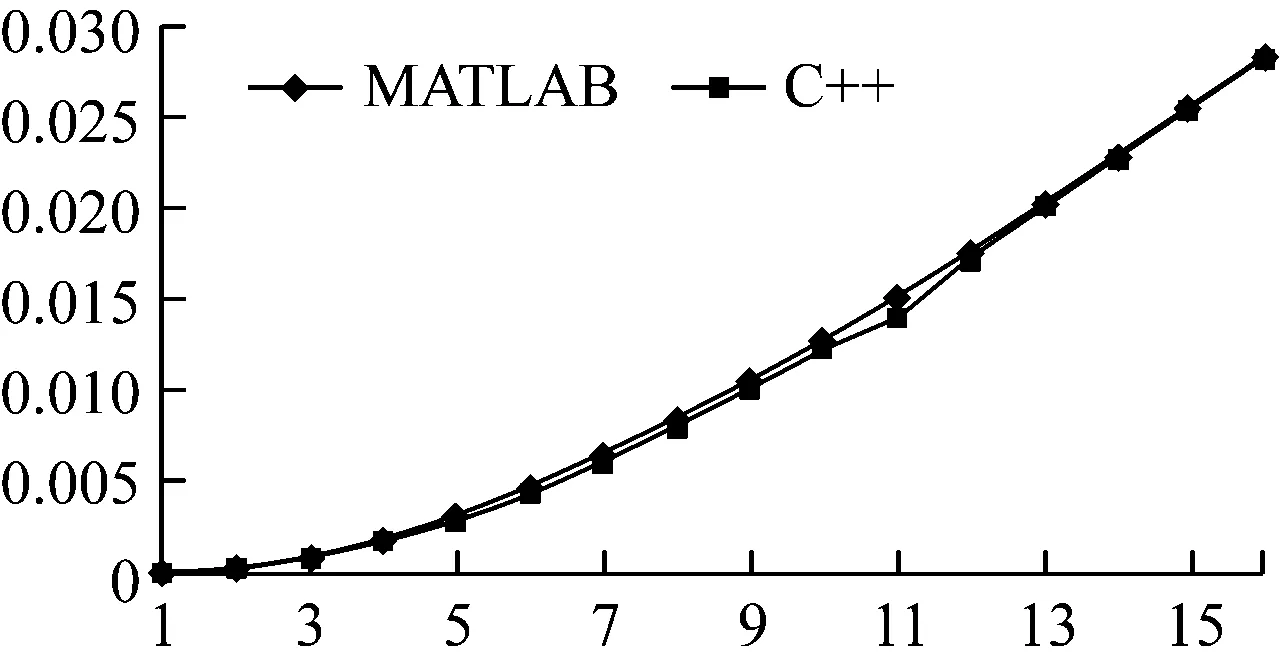
for (int i = 0;i { double x = coord[i]; double y = coord[i + 1]; double z = coord[i + 2]; p = P_Point(x,y,z); nodes.push_back(p); } 前處理分為3個部分:使用C++編程建模;輸入材料的各要素數值,如截面形狀及大小、載荷定義等;生成無網格方法分析所需要的節點數據。 在無網格方法前處理程序中,鏈接OpenGL庫直接使用C++語言建模,輸入各種幾何信息和物理信息,對模型信息屬性和邊界進行配置,以便建模成功后生成網格。網格應進行合適性判斷,減少節點距離過近、避免出現丟失邊界及穿透邊界的情況,再通過邊交換方法對三角形進行優化,提高三角形質量。 在求解域中選取適當分布的離散節點,根據一定的準則進行篩選以形成適合計算的結構。以二維問題為例,需要先確定一個點為中心點,再根據距離準則篩選出一定數量的衛星點,在這些衛星點中運用Delaunay準則進行臨時三角化處理,遍歷找出最合適的點云結構,最后采用改進的移動最小二乘法進行節點數據處理。 后處理程序讀取前處理的節點、單元等信息,獲取計算程序得到的位移等信息,并重新組織成標準后處理結果文件的形式,利用計算機可視化技術再現模型信息,將分析結果以圖像形式顯示出來。 本系統的后處理程序包括數據處理程序、圖像顯示程序等,具體內容包括3個部分:(1)模型數據(初始的節點編號、坐標等信息,以及計算程序得到的數據)的提取;(2)模型結果可視化處理,分析結果數據,重新構建模型的計算結果視圖;(3)結果數據查看,利用Visual Studio軟件的文件流函數將生成的數據直接存入文本文件。 前處理和計算程序產生的結果數據通常包括模型數據和結果數據,后處理程序采用文本文件存儲以上信息。文件接收網格節點等信息,并將其存儲到文本文件中,同時改變節點的空間坐標以達到將變形可視化的目標。文本文件網格節點等信息修正、顯示位移的操作程序如下。 //進行文件操作 int _total = getFileLine("*****");//獲取文件 總行數函數 int Nodes_row=getStrrow("*****","*****"); //獲取某文件的某一指定字符串的行數 ifstream fin("*****"); if (!fin) // 如果讀取失敗,打印fail { cerr <<"fail" < return; } ofstream fout("*****.txt");//創建一個新文件接收字符串 string s; int _index = 0; float data; while (getline(fin,s)) { if (_index <= Nodes_row || _index >= EndNodes_row) fout < else{ istringstream iss(s); vector while (iss >>data) { newdata.push_back(data); } bool is_chuan = false; int _L = newdata.size(); if (_L == 3){ double chuandi = dataprocess(newdata[0], deformedpoint); fout < else fout < _index++;} 采用基于點的近似構造逼近函數是無網格方法的關鍵。形成逼近函數的主要方法有光滑粒子法、移動最小二乘法和重構核粒子法等,其中移動最小二乘法應用最為廣泛,即 (1) 式中:為基函數的個數;()為基函數;()為待定系數。線性基函數 =[1] (2) 點鄰域內的局部逼近為 (3) 定義泛函數 (4) 式中:為點影響域內的節點;為影響域覆蓋點的節點數;(-)為定義的權函數。 ()=()() (5) 其中: ()=() (6) ()=() (7) 由以上計算可得逼近函數 (8) 式中:()為形函數, ()=[()() …()]= ()()() (9) 在移動最小二乘法中,當較大時,式(5)有時是病態的甚至是奇異的,難以獲得正確解或者難以求解。由此,采用改進的移動最小二乘法,選取正交函數作為基函數,得到的方程不但可以避免病態和奇異,而且不需要求解方程的逆,可直接得到該方程組的解 ()=()(), (10) 其中: (11) 將式(10)代入式(3),可得 (12) (13) 改進的移動最小二乘法求解系數()時不需要求解矩陣()的逆,可避免出現的病態或者奇異的方程組,因此可提高計算效率和精度。 基于改進的移動最小二乘法推導出二維彈性大變形問題和三維彈塑性問題的改進無單元Galerkin方法的方程。三維問題可囊括二維問題相關公式,對三維公式推導的介紹更具有代表性,所以此處只介紹三維彈塑性問題的方程推導過程。 彈塑性問題的平衡方程可表示為 (Δ)+Δ=0,∈, (14) 式中:(·)為微分算子矩陣;Δ為域內任一點的應力增量;Δ為域內任一點的體力增量。 (15) Δ=[ΔΔΔΔΔΔ] (16) Δ=[ΔΔΔ] (17) 彈塑性問題的幾何方程表示為 Δ=(Δ) (18) 式中:Δ為影響域內任一點的應變增量;Δ為影響域內任一點的位移增量。 彈塑性問題的物理方程表示為 Δ=Δ (19) 在彈性階段內和塑性階段內表達式不同。 定義邊界條件為 (20) (21) 在采用改進的無單元Galerkin方法求解彈塑性問題時,需要使用適當的方法將求解問題線性化,即使用一系列的線性解逼近非線性問題的解,例如采用逐步增加載荷的方法,按比例施加載荷。 由改進的移動最小二乘法的形函數表達式可得,域內任一點的位移增量向量可表示為 (22) 式中:為點影響域內的節點數。 應變張量可表示為 (23) 綜合上述推導,可得 (24) 對表達式進行替換,可得 (25) (26) (27) (28) (29) 若在應力邊界上點處作用集中力,則 (30) 式(26)可轉化為 (31) 3.3.1 數據處理 模型進行數值計算一般需要3類數據,分別為節點數據、單元數據和邊界條件數據。 節點數據主要包括節點的空間信息、編號,以及其對應的計算得到的位移等數據。 單元數據主要包括定義的材料特性(如彈性模量、泊松比和密度等相關信息)和物理特性(主要是幾何參數)。 邊界條件數據主要用以分析對象與外界的相互作用,主要包括位移約束和載荷條件。位移約束數據規定節點在自由度上所受到約束限制,載荷條件數據用于定義模型中節點載荷等力作用的位置、方向和大小。 同時,因為計算程序中的數值計算大多為矩陣運算,所以建立矩陣類class Matrix以及稀疏矩陣類class SparseMatrix,程序如下。 class Matrix { public: Matrix(); Matrix(int,int); Matrix(const Matrix &m); Matrix(int,int,double);//預分配空間 virtual ~Matrix();//析構函數 Matrix&operator=(const Matrix&);//矩陣的復制 int row() const; int col() const; private: int rows_num,cols_num; double **p; void initialize();//初始化矩陣 }; 矩陣類中部分函數定義如下。 double Point(int i,int j) const; //求矩陣的逆矩陣 static Matrix inv(Matrix); //矩陣加法 Matrix&operator+=(const Matrix&); //矩陣減法 Matrix&operator-=(const Matrix&); //矩陣乘法 Matrix&operator*=(const Matrix&); //求K矩陣 Matrix&Kjuzhen(Matrix,Matrix); class SparseMatrix { int nrLines,nrColumns; int nrElements;//非零元素數量 double* elements;//三元組的值存放 int* lines,*cols;//三元組的坐標 public: SparseMatrix(); SparseMatrix(int,int,double*,int*,int*); SparseMatrix(int,int,int,double*,int*,int*); SparseMatrix(const SparseMatrix&); ~SparseMatrix(); int getNumberOfLines(); int getNumberOfColumns(); int getElement(); } 稀疏矩陣中的部分函數如下。 friend SparseMatrix operator+(const SparseMatrix&,const SparseMatrix&); friend SparseMatrix operator-(const SparseMatrix&,const SparseMatrix&); friend SparseMatrix operator*(const SparseMatrix&,const SparseMatrix&); friend SparseMatrix operator*(const SparseMatrix&,double) 這些函數實現計算程序全部的矩陣運算,對矩陣的各種操作進行封裝,能大大提高計算效率。 3.3.2 數值流程 彈塑性問題的改進無單元Galerkin方法的數值計算流程如下。 (1)對結構視為完全彈性,施加全部載荷進行計算。 a.遍歷循環每個網格,對網格內的高斯積分點進行循環,判斷高斯積分點是否在域內,是則進行以下步驟,否則結束循環;確定高斯積分點影響域內的節點,然后計算積分點處的形函數及其導數;用式(30)計算等效剛度矩陣,保存該積分點對矩陣及等效節點載荷的貢獻; b.結束網格循環,得到剛度矩陣和等效載荷列向量Δ的第一項; c.進行邊界積分運算,用類似方法計算等效載荷列向量Δ的第二項; d.由第一項和第二項計算Δ; e.擬合各節點的位移、應力和應變等信息。 (3)施加載荷增量Δ; (4)按照式(25)計算剛度矩陣,要保證在彈性階段和塑性階段分別采用不同公式進行計算; (5)求解式(30),得到所有節點的位移增量,進而計算應變增量和應力增量,并把位移增量、應變增量和應力增量疊加到加載前的數據上; (6)若加載到全部載荷,則跳出循環; (7)輸出節點的位移。 對二維和三維受集中力的懸臂梁采用彈塑性問題的改進無單元Galerkin方法進行彈塑性大變形數值分析。對懸臂梁建模,利用前處理程序模塊在求解域中布置節點,并將節點信息輸入到編寫的C++數值算例程序,計算獲取節點處的位移和應力、應變數據,并將計算結果與使用MATLAB軟件得到的數值解進行比較,驗證改進無單元Galerkin方法以及程序的有效性。 自由端受集中力載荷的二維懸臂梁示意見圖2。梁的幾何尺寸為=8 m,=1 m,載荷=1 N,泊松比=0.25,屈服極限=25 Pa。材料的彈性模量為=1.0×10Pa,按平面應力問題求解。 圖2 受集中力的二維懸臂梁示意 采用前處理程序布置節點,結果見圖3。 圖3 二維懸臂梁節點分布 采用彈塑性問題的改進無單元Galerkin方法進行計算,將獲得的位移信息輸入后處理程序中,懸臂梁的變形見圖4,其位移量增大30倍。 圖4 二維懸臂梁變形 為驗證程序的準確性,將本文程序計算得到的數值解與MATLAB結果進行對比,見圖5。本文二維計算程序能夠得到滿意的結果。 圖5 二維懸臂梁的節點位移計算結果對比 自由端受集中力載荷的三維懸臂梁示意見圖6。梁的幾何尺寸為=8 m,=1 m,=1 m,其他材料特性與第4.1節相同,本文案例可采用線性強化彈塑性模型和MISES屈服準則。 圖6 受集中力三維懸臂梁示意 采用前處理程序布置節點,結果見圖7。將計算得到的數據輸入后處理程序中,模型的變形結果見圖8和9,其位移量增大15倍。 圖7 三維懸臂梁節點分布 圖8 三維懸臂梁實體變形 圖9 三維懸臂梁節點變形 將本文程序計算得到的數值解與MATLAB結果對比,見圖10。本文軟件的三維計算程序能夠得到滿意的結果。 圖10 三維懸臂梁的節點位移計算結果對比 采用C++語言開發彈塑性問題的改進無單元Galerkin方法計算軟件,實現快速建模和對離散點集進行前處理后的數據采集,采用改進無單元Galerkin方法的程序計算結果,將得到的節點信息和邊界條件等信息以文件形式輸入到后處理程序中,實現結果圖形可視化。通過數值算例分析,驗證本文方法的有效性和優越性。 在后續工作中,在前處理程序中將加入更多程序模塊,完善模型的邊界條件處理和組件功能等程序;計算程序模塊將加入彈性大變形和彈塑性大變形等問題的計算程序,以支持復雜問題的數值分析,為形成完善的無網格方法計算軟件奠定基礎。2.2 后處理程序
3 計算程序
3.1 改進的移動最小二乘法
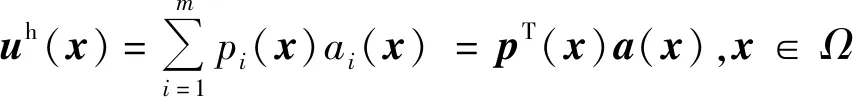

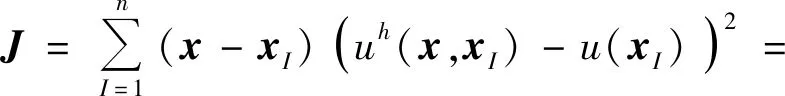
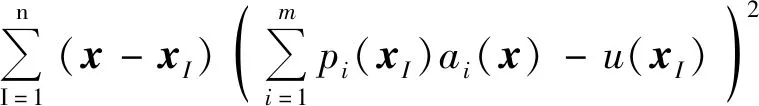
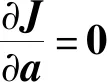
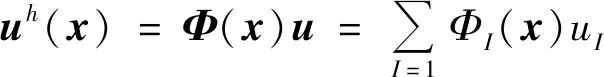
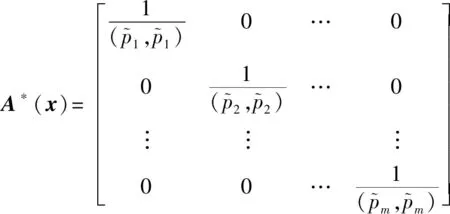
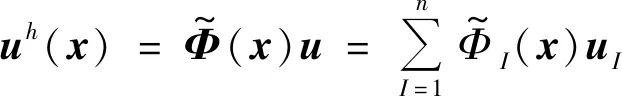
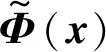
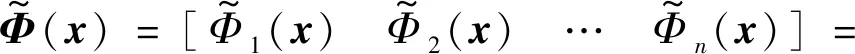
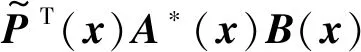
3.2 彈塑性問題的改進無單元Galerkin方法
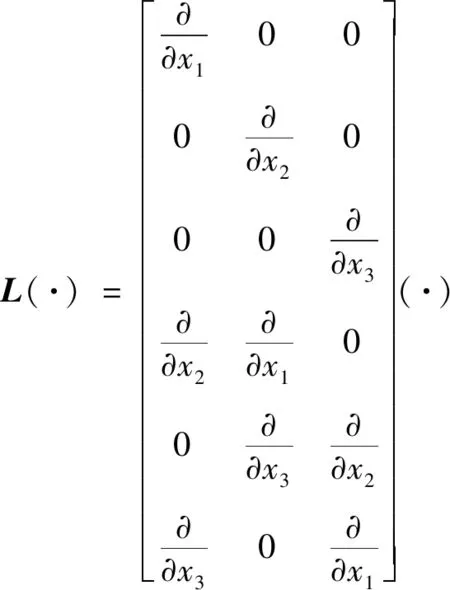
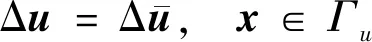
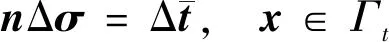
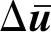
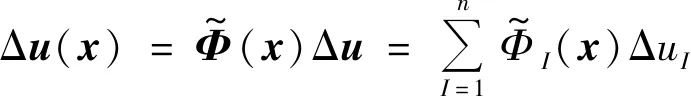
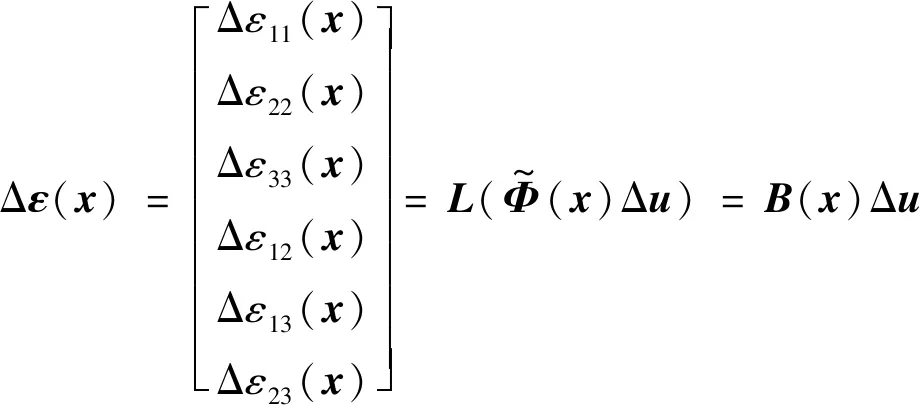
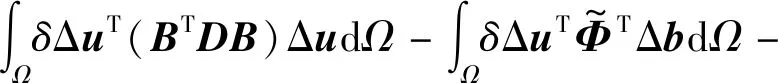
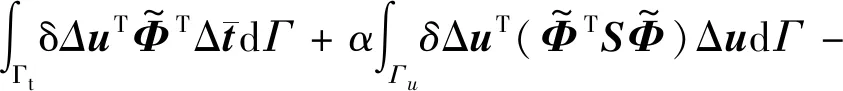
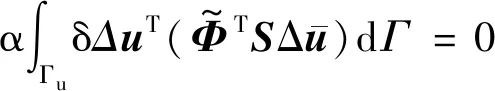



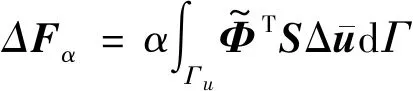
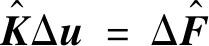

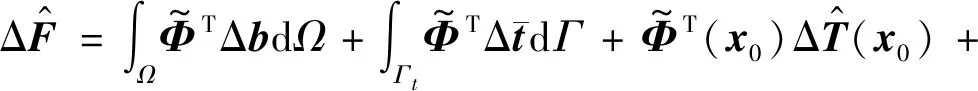
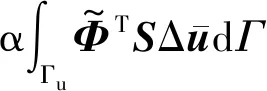
3.3 彈塑性問題的改進無單元Galerkin方法計算程序開發
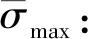
4 數值算例
4.1 二維算例



4.2 三維算例

5 結 論

