談高中數學教學中合情推理的價值與應用

馬婷

江蘇省揚州市江都區丁溝中學 225200

在高中數學教學中推理的地位至關重要，可以說如果沒有推理數學知識就很難被建構起來.當然，高中數學教學中強調得更多的是邏輯推理，比如《普通高中數學課程標準（2017年版）》就將邏輯推理作為數學學科核心素養的組成要素之一.邏輯推理的重要性不言而喻，但是還有一種看起來水平較低的推理也應當引起高中數學教師的重視，這個推理就是合情推理.通常情況下，合情推理更多發生于數學基礎知識的學習過程中，但如果不是站在數學知識的角度，而是站在學生學習的角度來看高中數學教學中的推理，又可以發現合情推理在高中數學教學中應當有一席之地.

之所以提出這個觀點，是因為相當一部分學生在高中數學知識學習的過程中，由于思維方式等的差異，還需要合情推理來奠定包括邏輯推理在內所有數學學科核心素養要素養成的基礎.而且就算從數學知識發生的角度來看，不少高中數學概念或者規律，依然需要用合情推理來打開大門.所以合情推理在高中數學教學中應當被重視，而且學生學習高中數學一定是離不開合情推理的.如果以往高中數學教育較為注重嚴謹性的論證演繹推理，那么隨著對學生學習過程的重視程度越來越高，引導學生進行合情推理并在此基礎上進行合理猜想，然后讓學生在學習過程中主動發現并提出問題，進而通過推理猜想探索數學規律，引導學生進行合情推理和猜想就應當成為高中數學教學的一個重要任務［1］.

本文借助“函數的單調性”教學，談談高中數學教學中合情推理的價值與應用途徑.

合情推理在高中數學教學中的價值

一般認為，合情推理是指合乎情理的、似乎真的推理，因此又被稱為“似真推理”.相對于邏輯推理而言，合情推理并不過于強調邏輯性，即使依賴直覺進行推理也是可行的.自然而然的合情推理，也不追求結果的百分之百的準確，但要求學生的思維能夠向數學規律靠近.因此，合情推理的清晰程度并不能與數學中的論證推理相比，其是一個沒有固定的邏輯，是籠統的但又合乎情理的推理.因此合情推理并不能獲得所有人的認同，但是盡管如此，合情推理在數學中依然有論證推理不能替代的作用，它對于數學的創造性發展有著重大意義與價值.

具體來說，合情推理在高中數學教學中的價值表現為：合情推理能夠幫助學生打開數學感知的大門，能夠引導學生在數學情境中完成從生活向數學的轉變.這一點對于幾乎所有高中生來說都是有積極意義的，因為學生如果不能在這個環節觸摸數學學習的本質，那就不能進行有效的數學學習，因此合情推理才是消解學生數學學習困難、減少高中數學教學中常常出現的兩極分化現象的關鍵之一.除此之外，合情推理還能夠促進學生的思維從淺層走向深度，從膚淺走向深刻，從某種程度來講，合情推理就是學生思維遞進的一個重要臺階.

比如，“函數的單調性”這一知識看起來簡單，卻是學生理解函數性質的一個重要節點.從數學意義的角度來看，學生對函數單調性的理解是建立在其定義之上的，而這種定義的抽象性，會讓不少學生望而生畏.相應地，在這一知識的學習過程中，如果學生能夠利用合情推理來打開探究的大門，那么就能夠讓學生對合情推理的理解變得更加高效.

合情推理在高中數學教學中的應用

那么在具體的應用過程中，合情推理應當如何實施呢？筆者也分析了一些教學案例，結果發現很多教師都是給學生一個情境，然后直接讓學生去猜想，很多時候可能都會因為情境創設不恰當或者問題設計不科學，學生很難進行有效的猜想.因此，合情推理的應用實際上是有一定技術要求的.有研究者研究數學教學、培養學生合情推理的能力時，提出“善用教材，尋求合情推理的切入點”“依照數學原理，進行合情推理教學”“設置情境，鼓勵學生合理猜想”“拓展類比，推進合理推理的轉化”“營造良好的課堂氛圍，促進學生不斷地自我探索和創新”［2］，這樣的闡述對于合情推理的應用來說，有著一定的啟發，也就是說，教師應當認真研究教材，確定合理的合情推理切入點，然后從學生的認知基礎出發引導學生進入情境，進而在問題的驅動下進行合情推理.

例如，在“函數的單調性”教學中，筆者先給學生呈現了多個函數的圖像（如圖1、圖2所示），然后讓學生去觀察這些圖像，思考如何從圖像上發現這些函數的性質.這是一個學生進行觀察并猜想的過程：憑著直覺思維可以發現這兩個圖像都對應著一定的變化規律，但是這個變化規律又不能簡單地描述出來，于是學生發現應當將這兩個函數進行分段分析，才能準確地描述它們的性質.

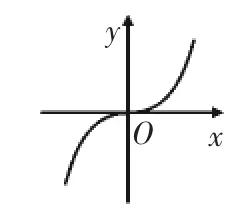
圖1

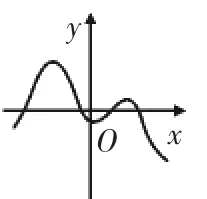
圖2

具體分析學生的這一思考過程可以發現，學生最初描述這些性質的時候，用的是“變大”或“變小”這樣的生活用語；而問學生為什么會這么描述，學生會說直接從圖像上看到的.

這樣一個學生直接觀察的過程，實際上對應的是學生的直覺思維，而變大與變小則是基于圖像走勢的直觀判斷.從圖1的單一變化到圖2的復雜變化，學生容易猜想到如果遇到的是更為復雜的函數及其圖像，要描述其性質，就需要進行分段描述，自然也就有學生會在這個過程中提出問題：如果要分段的話，應當如何分段呢？如果要描述函數性質的話，應當如何描述呢？在這一些問題的驅動下，學生的探究會逐步深入，有不少學生提出應當遵循由易到難的原則，先選擇一個相對簡單的函數圖像去研究其性質.這時可以引導學生以二次函數f（x）=ax2（a≠0）作為研究對象，那么學生就可以觀察到，無論是開口向上還是開口向下，都需要將二次函數的圖像分成兩部分來闡述……

事實證明，有了上述這樣一段分析過程作為基礎，學生認識函數單調性時，整個過程就會非常順利.這顯然得益于合情推理：學生最初的變大或變小的認識，就是合情推理的結果；后面學生提出的問題，也是合情推理的結果.如果沒有學生的這些合情推理，如果只是教師純粹的講授，那么在學生的思維當中，就沒有這些合情推理的結果作為緩沖與潤滑，學習結果自然也就不會理想.

合情推理在高中數學教學中的概括

從以上的理論分析與實踐探究來看，合情推理在高中數學教學中的價值，主要體現在合情推理能夠在學生學習數學概念或者規律的過程當中，生成許多默會的知識，有了這些默會的知識，那么學生在建構這些數學知識時，過程就會更加自然.對于教師來說，判斷并評價學生的合情推理，主要依據的是學生的學習結果.如果教師此前給足了學生進行合情推理的空間，而學生在后續學習與運用知識時又變得更加自然，那么就可以認為這樣的合情推理是成功的.

雖然合情推理不像邏輯推理那樣具有相對單獨且重要的意義，但是要想提升學生的數學學習品質，教師有必要將合情推理作為一個重要的教學內容.除了讓學生在知識發生的過程中進行合情推理外，要想讓學生進行更好的合情推理，教師可以讓學生去欣賞一些偉大的猜想產生的過程.在這些過程當中，也蘊含著豐富的合情推理環節，讓學生體會并認識到如何利用合情推理去猜測和發現一些新的結論，也可以培養學生進行合情推理的思維方式，同時對后繼知識的學習起到引領的作用.

總而言之，高中數學教學必須重視合情推理，要讓合情推理成為學生學習數學知識的有效緩沖，要讓合情推理的結果成為學生建構數學知識的有效補充.將合情推理納入高中數學教學的內容范疇，在教學中賦予學生更多的合情推理空間，是數學教師應當重視并努力的方向.