金屬磁記憶應變誘導磁性變化的原子尺度作用機理*

王思遠 梁添壽2) 時朋朋?

1) (西安建筑科技大學土木工程學院,西安 710055)

2) (西安建筑科技大學機電工程學院,西安 710055)

基于力磁耦合效應的磁記憶檢測技術,被廣泛應用于鐵磁性結構件的應力和缺陷檢測.已有研究采用第一性原理針對α-Fe 體系開展了軸向拉壓作用下磁矩變化計算,初步討論了原子層面的磁檢測技術力磁耦合機理.本文以Fe-C 和Fe-Mn 摻雜體系為例,在更為復雜的拉伸、壓縮和剪切加載情形下,深入討論了α-Fe 材料不同類型原子摻雜體系中磁矩變化等力磁耦合規律機理.結果表明,α-Fe 和摻雜體系在不同類型應變作用下磁矩和能量的變化規律存在不同.結合態密度、能帶結構和原子磁矩的詳細分析,發現摻雜元素通過影響Fe 原子的磁矩,使摻雜體系能帶結構的形貌和態密度的峰值發生改變,進而導致摻雜體系的磁矩和能量變化規律存在差異.本研究從原子層面考慮了鐵磁材料在不同荷載類型、不同摻雜元素和含量下的力磁耦合效應,是磁記憶檢測中多場耦合物理機理的重要補充.

1 引言

彈性應變工程研究受到廣泛應用,這是由于應力應變對力學性能[1]、材料屬性[2]和電磁特性[3]等特征存在重要影響.隨著材料建模方法和計算科學的發展,基于密度泛函理論(DFT)[4]的第一性原理計算方法成為了材料設計、合成、模擬計算和評價等的重要研究方法[5-8].由于晶體結構、系統能量和電子自旋密度分布與原子磁矩等材料磁性密切相關,第一性原理計算可用于分析原子尺度的應力應變對磁性的作用規律,這對力磁作用相關的彈性應變工程技術提供了新的研究角度和手段.

一些彈性應變工程的實現是利用了材料中的力磁耦合效應[9,10].力磁耦合效應是應力引起的磁導率變化導致鐵磁材料表面磁感應強度發生改變的現象[10-12].磁致伸縮效應的觀察可以追溯到1842年,重點討論外加磁場引起的材料機械響應[13].此外,學者們對通過應力調節材料磁性產生極大興趣[14-16].Shi 等[17]和Doubov 等[18-21]提出了金屬磁記憶(MMM)無損檢測技術,可用于檢測鐵磁結構中的應力集中和缺陷.MMM 檢測技術的原理為鐵磁材料的力磁耦合效應[22,23].近年來,一些學者通過第一性原理計算外載荷作用下的電子密度分布,以研究應力-應變對鐵磁材料磁性的影響,解釋磁記憶效應產生的微觀機制.Yang 等[24]研究了原子磁矩與壓力的關系,發現當壓力增大時,自旋極化體系中原子磁矩線性減小，并針對晶胞受壓和受拉兩種情形[25]計算了α-Fe晶體磁性能與應變之間的定量關系.值得注意是,上述提到的磁檢測技術相關的第一性原理分析僅考慮了α-Fe 體系軸向應變作用導致的原子磁矩變化機理.考慮到實際工程中存在不同的材料類型,如硅鋼、碳鋼、錳鋼等.不同原子類型和含量下的力磁耦合機制存在差異,相關研究對深入理解不同材料磁檢測規律的差異至關重要.拉伸、壓縮和剪切等不同荷載類型下力磁耦合效應的差異也是一個值得關注的問題.

為了闡明原子層面的力磁耦合關系,本文以Fe-C 和Fe-Mn 摻雜體系為例,在更為復雜的拉伸、壓縮和剪切加載情形下,研究了金屬磁記憶應變誘導磁性變化的原子尺度作用機理.計算了α-Fe 和摻雜C,Mn 元素的摻雜體系在拉伸、壓縮和剪切應變作用下的磁矩和能量,發現不同體系的磁矩和能量隨應變表現出差異,同時從態密度圖、能帶結構圖和原子磁矩三個方面分析不同體系間的磁特性存在差異的原因.

2 模型建立和計算方法

這里采用基于密度泛函(DFT)的第一性原理計算從原子尺度揭示應力應變對體系磁性作用機理和規律.本文采用基于平面波的DFT 計算方法,該方法廣泛應用于結構磁特性的計算[26,27].通過平面波來展開晶體波函數,并用贗勢方法作有效的近似處理,基于密度泛函理論的PW-PP 方法[28]可以方便地對大范圍體系的基態屬性進行有效精確計算[29].本文計算采用CASTEP 程序包[30],其中交換關聯泛函采用的是廣義梯度近似下的Perdew-Burke-Ernzerhof (PBE)泛函[31].首先通過優化截斷能量取值和k點選取,獲取合適的計算參數確保計算的收斂性,詳細的收斂性測試見附錄中的圖A1.根據優化結果,本文采用平面波截斷能量480 eV,布里淵區采樣k點網格為6×6×6,能量計算精度達到0.01 eV/atom.利用上述參數,對單胞晶格進行優化,獲得的磁矩為2.17μB.從理論計算結果來看,本文的計算結果與文獻[25]和文獻[34]報道的理論計算結果2.17μB一致.此外,文獻[35]和文獻[36]報道的實驗測量值分別為2.22μB和2.12μB.由此可知,理論計算結果在實驗測量誤差范圍內.在基態單胞基礎上建立了α-Fe(BCC)2×2×2超胞結構,圖1(a)給出超胞受到拉伸、壓縮和剪切應變作用下的計算模型示意圖.其中,拉伸和壓縮應變為變化后的晶格長度與初始晶格常數的比值;對于剪切應變加載,應變大小表示為剪切夾角γ.

圖1 拉伸、壓縮和剪切作用引起的α-Fe 磁矩(M)和能量增量(ΔE)的變化圖 (a) α-Fe的2×2×2 超胞在拉伸、壓縮和剪切應變作用下的計算模型;(b) 磁矩變化;(c) 能量增量Fig.1.Variation of α-Fe magnetic moment (M) and energy increment (ΔE) induced by tension,compression and shear strain: (a) Model of α-Fe 2×2×2 supercell under tensile,compressive and shear strain;(b) Change of magnetic moment;(c) Increment of energy.

圖A1 收斂性測試 (a) 截斷能收斂測試;(b) k 點取值收斂測試;(c) α-Fe 晶胞的能量收斂過程;(d) Fe-C(1)晶胞的能量收斂過程Fig.A1.Convergence test: (a) Cut-off energy test;(b) k-point value test;(c) Energy convergence process of α-Fe;(d) Energy convergence process of Fe-C(1).

圖1(b)和圖1(c)給出了晶胞磁矩和能量隨拉伸、壓縮和剪切三種應變加載的變化規律,其中能量的相關解釋見附錄A.總體上,α-Fe 超胞的磁矩和能量均隨應變的增大而增大,但變化趨勢和程度存在差異.剪應變作用下變化值分別為0.1045μB和0.0169 eV,拉應變作用下變化值分別為0.04162μB和0.0095 eV,壓應變作用下變化值分別為0.00136μB和0.0081 eV.由此可知,剪應變作用對α-Fe 磁矩和能量的影響最大,拉伸作用次之,而壓縮作用最小.參見附錄中的表A3,本文計算的磁矩變化與文獻[25]的相關結果保持一致.

表A3 不同應變作用下α-Fe 體系的磁矩和能量變化Table A3.The magnetic moments and energies of a-Fe under different types of strain.

3 結果討論

3.1 應變作用下摻雜體系磁特性

這里對比討論了摻雜元素C 和Mn 對α-Fe體系磁特性的影響.圖2(a)給出了在α-Fe 超晶胞結構基礎上構建的Fe-C 和Fe-Mn 兩種摻雜體系模型示意圖.此處考慮了采用C 或Mn 原子替換位于超晶胞中心Fe 原子和關于中心對稱的兩個Fe 原子的不同替換方式.計算得到Fe-C(1),Fe-C(2)和Fe-Mn 晶格常數分別為2.8145,2.7907 和2.8323 ?,對于不同C 含量的摻雜,Fe-C(2)的晶格常數為2.7907 ?,小于Fe-C(1)的2.8145 ?.圖2(b)分析了計算得到的拉伸、壓縮和剪切三種應變加載情形下,摻雜體系能量增量隨應變加載的變化規律,詳細的計算結果見附錄表A4.對于三種不同類型的應變加載,摻雜體系的能量均隨著應變的增加而增加.拉伸應變加載下,Fe-C(2)體系的能量明顯增加,變化值為0.0186 eV,而Fe-Mn 體系的能量略有增加,變化值為0.0095 eV.在壓縮應變加載下,Fe-C(1)體系的能量隨著應變的增加而迅速增加.由于剪切應變作用下的晶格形狀相較于拉伸和壓縮應變作用下有明顯改變,因此剪切應變下摻雜體系的能量變化明顯且變化值在0.0227—0.0273 eV 之間.圖2(c)計算了Fe-C 和Fe-Mn 摻雜體系在不同類型應變作用下的磁矩變化規律,這可以作為鐵磁材料磁性的重要參數之一,詳細的計算結果見附錄表A5.Fe-Mn 體系的磁矩在不同應變作用下均隨應變增加而增加,但Fe-C 體系卻表現出不同的趨勢,不同應變作用下,與Fe-C(2)相比Fe-C(1)磁矩變化較為明顯.Fe-C(1)的磁矩隨拉應變增加而增加,當拉應變達到2%時其增長趨于平緩,但在壓縮和剪切應變作用下其磁矩有明顯下降的趨勢.在拉伸和剪切應變作用下,Fe-C(2)體系磁矩隨應變增加而增加,但在壓應變作用下有小幅度下降,變化量僅為0.03μB.從圖2(c)可以看出,Fe-C 和Fe-Mn 體系在應變作用下的磁矩變化規律存在差異.

圖2 摻雜元素對α-Fe 體系磁特性的影響 (a) 2×2×2 超晶胞及摻雜1 個或2 個原子的摻雜體系模型;(b) 不同類型應變作用下的能量增量 ΔE;(c) 不同類型應變作用下磁矩M的變化Fig.2.Effect of doping elements on magnetic properties of the α-Fe system: (a) 2×2×2 supercell structure and supercell structure doped with one or two atoms;(b) Energy increments (ΔE)under different types of strain;(c) Change of magnetic moment under different types of strain.

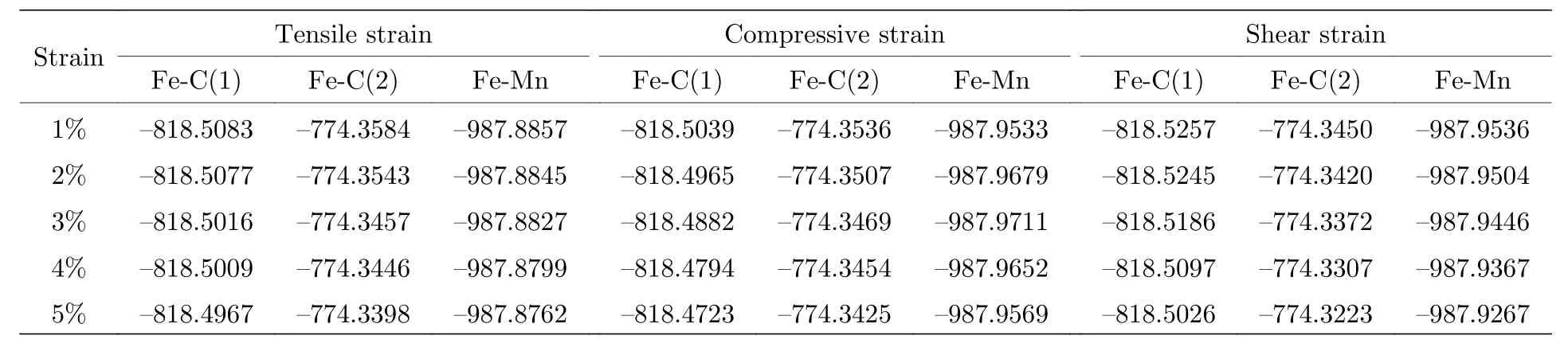
表A4 三種不同應變加載方式下摻雜體系能量的變化(eV)Table A4.Variation of the energy in doping systems under three different types of strain loading (eV).

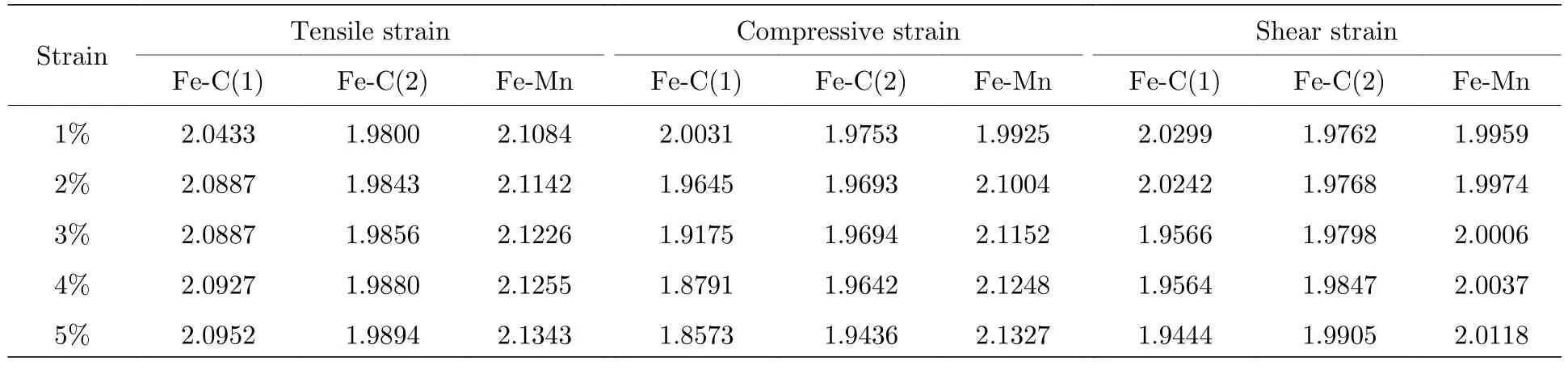
表A5 不同應變作用下摻雜體系的磁矩變化Table A5.Variation of the total magnetic moment of doping systems under different strain states (μB) .

3.2 能帶結構和態密度

為了揭示α-Fe 與摻雜體系磁矩產生差異的原因,本文基于平衡結構計算了摻雜體系布里淵區(BZ)沿高對稱線的能帶結構和態密度(DOS),布里淵區路徑為Г(0,0,0) —F(0,1/2,0) —Q(0,1/2,1/2) —Z(0,0,1/2) —Г(0,0,0).詳細的摻雜體系能帶結構見附錄圖A3.摻雜C 和Mn 元素后能帶結構有了顯著改變,同時費米能級附近的導帶和價帶相交,這意味著摻雜C 和Mn 元素后體系仍保持金屬性.在此基礎上進一步比較了α-Fe 初始狀態和施加三種不同類型應變加載后的能帶結構,揭示了晶體中電子運動的特征.從圖3 中的能帶結構可知,α-Fe初始狀態以及施加應變后的能帶結構在費米能級附近(紅色虛線)的導帶和價帶相交,電子可以無障礙地達到導帶,形成導電能力并表現出明顯的金屬性.圖3(a)和圖3(b)比較了應變前后α-Fe的能帶結構,應變會使能帶結構發生改變,但不同類型應變加載對其影響較小,如圖3(b)—(d)所示.

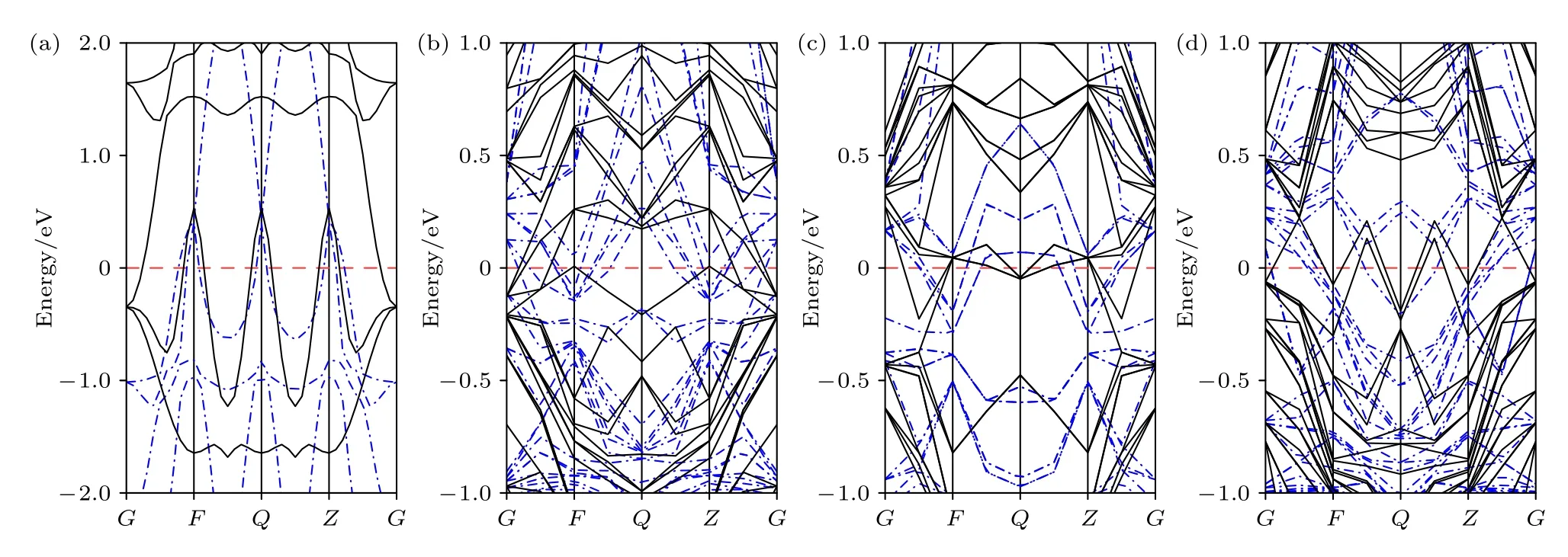
圖A3 無應變作用下α-Fe 及其Fe-C 和Fe-Mn 摻雜體系的能帶結構 (a) α-Fe;(b) Fe-C(1);(c) Fe-C(2);(d) Fe-MnFig.A3.Band structure of α-Fe and its C-and Mn-doped systems without strain: (a) α-Fe;(b) Fe-C(1);(c) Fe-C(2);(d) Fe-Mn.

圖3 拉伸、壓縮和剪切應變作用下α-Fe的能帶結構圖 (a) 初始狀態;(b) 5%拉應變;(c)5 %壓應變;(d) 5%剪應變Fig.3.Band structure diagram of α-Fe under tensile,compression and shear strain: (a) Initial state;(b) 5% tensile strain;(c) 5%compressive strain;(d) 5% shear strain.

為揭示能量上不穩定的潛在機制,分析了摻雜體系的電子態密度.能量E在E -(E+ΔE)范圍內的電子能態數目為ΔZ,則能態密度為

其中N(E)為能態密度(或態密度)以及ΔE為能量的變化量.能態密度描述了電子態的能量分布,由態密度的定義式(1)可推出,第n個能帶的態密度Nn(E)為

式中Ω為原胞體積,N為晶體中原胞總數,En(k)為等能面,在布里淵區內進行積分.態密度總和N(E)為所有能帶的態密度之和,即

在SE上進行積分,NΩ為晶體體積,dS為面積元,?kE(k)是En(k)的梯度.基于 (3) 式,可以得到拉伸、壓縮和剪切應變加載過程中摻雜體系的DOS變化.

圖4(a)給出了摻雜C 和Mn 兩種自旋電子的自旋態密度分布,在費米能級附近電子自旋態密度的分布相似,說明磁性行為相似,結果表明摻雜C 和Mn 元素后的摻雜體系仍然保留鐵磁性.本文也研究了摻雜C 和Mn 原子各軌道對總態密度的貢獻,d,s 和p 三個軌道電子分波態密度(PDOS)的分析結果見附錄圖A4.摻雜體系中Fe 原子的d 軌道電子PDOS 與體系總自旋態密度最為相似,且態密度曲線的自旋向上態與自旋向下態在費米能級附近劈裂狀態顯著,說明Fe 原子的d 軌道電子對摻雜體系的磁性貢獻最大,在力磁耦合關系中起主要作用.摻雜的C 原子s 和p 軌道電子分波態密度曲線峰值較小,態密度曲線的自旋向上態與自旋向下態在費米能級附近劈裂狀態不顯著,說明C 原子不顯磁性且對體系總自旋態密度貢獻較小.特別地,摻雜的Mn 原子d 軌道電子分波態密度在費米能級表現出不對稱性,Mn 原子表現出磁性同時對總自旋態密度有一定的貢獻.這也解釋了Fe-Mn 體系的磁矩大于Fe-C 體系的磁矩.圖4(b)討論了拉伸、壓縮和剪切應變加載對摻雜體系總DOS 峰值的影響.費米能級附近峰值的大小存在明顯差異,特別是剪切應變作用下Fe-Mn 體系峰值49.71781 eV 與Fe-C(2)體系峰值38.01658 eV相差11.70123 eV.觀察到拉伸、壓縮和剪切作用下Fe-Mn,Fe-C(1)和Fe-C(2)在費米能級附近的峰值依次減小,DOS的峰值越高表明此區域中電子數量越高其磁性越高,這解釋了摻雜體系的磁矩Fe-Mn ＞ Fe-C(1) ＞ Fe-C(2).

圖4 電子態密度圖 (a) 不同體系自旋態密度;(b) 不同類型應變對摻雜體系DOS 峰值的影響;(c) 不同類型應變加載對摻雜體系雙峰間距的影響Fig.4.The density of states diagram: (a) Spin DOS of different systems;(b) Effects of different types of strain on DOS peaks of doping systems;(c) Effects of different types of strain loading on the spacing of double peaks in doping systems.

圖4(c)統計了拉伸、壓縮和剪切應變加載過程中Fe-C 和Fe-Mn 體系在費米能級附近兩個主峰的間距.隨著應變的不斷增加Fe-C 和Fe-Mn 體系在費米能級附近兩個主峰的間距表現出明顯差異,計算結果見圖A5,Fe-C 和Fe-Mn 體系的上下自旋電子的態密度在費米能級附近均存在峰值很大的尖峰且呈劈裂狀態,兩個主峰分離較大說明摻雜體系在應變加載過程中仍表現出較強磁性.圖4(c)顯示,對于Fe-C(1)體系,壓縮應變作用下兩個峰的間距從2.9847 eV 減小到2.8964 eV,剪切應變作用下兩個峰的間距從3.0089 eV 減小到2.9961 eV,拉伸應變則表現出截然相反的變化,兩個峰的間距從3.0411 eV 增大到3.2054 eV.電子分布向費米能級靠近,軌道電子局域性增強的同時系統磁性減弱,最終表現為壓縮和剪切應變作用下磁矩的不斷減小,拉應變與之相反則表現為磁矩隨應變不斷增加.Fe-C(2)和Fe-Mn 體系在費米能級附近兩個主峰的間距變化規律與磁矩變化保持一致.計算表明費米能級附近不同的電子分布是導致Fe-C 和Fe-Mn 體系的磁矩隨應變表現出差異的原因.

圖A5 摻雜體系在不同應變類型作用下(拉伸、壓縮和剪切)的自旋態密度圖 (a) Fe-C(1)體系DOS;(b) Fe-C(2)體系DOS;(c) Fe-Mn 體系DOSFig.A5.The spin density distribution of states of doping systems under different types of strain (tensile,compression and shear strain): (a) DOS changes of Fe-C(1) doping system;(b) DOS changes of Fe-C(1) doping system;(c) DOS changes of Fe-Mn doping system.

3.3 摻雜原子對總磁矩改變的貢獻

不同應變加載方式可以調節摻雜元素對體系磁性能的影響,這里比較了原子磁矩和總磁矩的變化趨勢,結果如圖5 所示.對于拉伸、壓縮和剪切應變加載,Fe 原子與總磁矩的變化趨勢一致,表明整個體系的磁矩以Fe 原子為主要貢獻.對于Fe-C 體系,C的原子磁矩隨著應變的增大發生小幅的減小,總磁矩變化是由于摻雜的C 元素影響Fe的原子磁矩,進而使總磁矩發生改變.隨著C 元素含量的增多,Fe-C(2)體系中C的原子磁矩相較于Fe-C(1)進一步減小,這是導致Fe-C(1)和Fe-C(2)在應變作用下,其磁矩變化產生差異的原因.特別地,Fe-Mn 體系中Mn的原子磁矩數值相較于Fe-C 體系中C的原子磁矩較大,Mn的原子磁矩在應變作用下表現出與總磁矩截然相反的變化趨勢.摻雜的C 原子s 和p 軌道電子分波態密度的自旋向上態與自旋向下態在費米能級附近的分布劈裂不顯著,摻雜元素C的p 軌道電子對體系總自旋態密度有微弱貢獻.與之相反的是摻雜Mn的p 軌道和d 軌道在費米能級附近的分布具有明顯的劈裂,說明Mn的d 軌道電子對體系的磁性有貢獻,如附錄圖A4 所示.這里,從分波態密度的角度解釋了Fe-Mn 體系中Mn的原子磁矩數值大于Fe-C 體系中C的原子磁矩.

圖A4 不同軌道電子分波態密度 (a) Fe-C(1)分波態密度;(b) Fe-C(2)分波態密度;(c) Fe-Mn 分波態密度Fig.A4.Different orbitals of PDOS: (a) PDOS of Fe-C(1);(b) PDOS of Fe-C(2);(c) PDOS of Fe-Mn.

圖5 C 和Mn 摻雜體系原子磁矩隨三種不同應變加載方式(拉伸、壓縮和剪切)的變化Fig.5.Variation of atomic magnetic moment with the three different types of strain loading (Tensile,compression and shear strain)for C-and Mn-doped systems.

隨著應變的增大,Fe-Mn 體系總磁矩隨著Mn原子磁矩的減小而增大,明顯區別于Fe-C 體系中C 元素對總磁矩的影響方式,這意味著Mn 摻雜原子的存在影響了體系的態密度,使Fe-Mn 體系的磁特性發生改變.由于不同摻雜元素對總磁矩的作用方式不同,導致Fe-C 體系和Fe-Mn 體系在不同應變作用下磁矩變化規律存在差異.結合態密度、能帶結構和原子磁矩的詳細分析發現,摻雜元素的存在使摻雜體系能帶結構的形貌和態密度的峰值發生改變,也導致摻雜體系的磁矩和能量變化規律存在差異.

4 結論

本文以Fe-C 和Fe-Mn 摻雜體系為例,深入討論了α-Fe 材料不同類型原子摻雜體系中磁矩變化等力磁耦合規律機理.采用密度泛函理論平面波贗勢法,運用GGA 法從原子層面計算了α-Fe 及其摻雜C 和Mn 兩種元素摻雜體系的力磁耦合效應,分析了拉伸、壓縮和剪切三種應變對Fe-C 和Fe-Mn 體系磁特性的影響,得到以下結論:

1)通過計算α-Fe 在拉伸、壓縮和剪切應變作用下的磁矩和能量變化,發現在不同類型應變作用下磁矩和能量變化規律存在差異,其中剪切應變作用對α-Fe 磁矩和能量的影響最大,拉伸作用次之,而壓縮作用最小.

2)討論了在拉伸、壓縮和剪切應變作用下摻雜C 和Mn 對鐵磁材料磁特性的影響,對比拉伸、壓縮和剪切三種不同應變加載方式,剪切應變下Fe-C 和Fe-Mn 體系的能量變化明顯.相同應變作用下Fe-C 和Fe-Mn 體系的能量和磁矩變化規律存在差異,摻雜C 和Mn 元素會對應變誘導磁矩增強產生影響.

3)結合態密度、能帶結構和原子磁矩的詳細分析,發現摻雜元素的存在使摻雜體系能帶結構的形貌和態密度的峰值發生改變,也導致摻雜體系的磁矩和能量變化規律存在差異.

第一性原理可為微觀磁疇動力學提供基礎參數,微觀動力學可為宏觀磁場信號分析提供非線性磁導率等基本參數,進而采用宏觀磁場有限元分析可為磁信號的定量規律計算提供可能.本文研究結果從原子層面展示了鐵磁材料在不同荷載類型、不同摻雜元素和含量下的力磁耦合效應機理和規律,是磁記憶檢測中多場耦合物理機理的重要補充.

附錄A

CASTEP 處理金屬系統使用基于K-S 方程的密度泛函理論計算晶胞的總能量[32]:

其中,EKS為Kohn-Sham 能量,T為Smearing 溫度,S為Mermin 熵.

這里給出了超晶胞體系總能量的CASTEP 計算結果包含: Final energy(E) ,Final free energy(E?TS) ,NB est.0 K energy(E ?0.5TS).Final energy(E)為忽略熵的Kohn-Sham 能量EKS,Final free energy(E?TS) 則為考慮溫度的自由能.密度泛函計算中,Kohn-Sham 能量和S均對Smearing 設置存在一階依賴關系,所以 NB est.0 K energy(E ?0.5TS) 將Smearing引入的熵進行平均考慮獲得T=0K時近似精確的體系總能量.固體的物理性質與其總能量有著密切的關系,故本文選擇校正形式的E ?0.5TS來獲得近似精確的體系總能量.

為了比較自旋極化和非自旋極化兩種狀態的相對穩定性,計算了兩種狀態下摻雜體系的總能量,定義了自旋極化能 ΔE=Es?Ens.其中Es和Ens分別為自旋極化狀態和非自旋極化狀態下摻雜體系的能量.自旋極化能計算結果如表A1 所列.自旋極化態能量較低,表明系統的自旋極化態比非自旋極化態更穩定.

表A1 平衡態α-Fe 及摻雜體系的自旋極化能Table A1.Spin polarization energy of equilibrium α-Fe(BCC) and doping systems.

表A2 給出了無應變α-Fe的晶格常數、原子體積和磁矩的計算結果,與文獻[34]結果保持一致,證明了本文計算過程的正確性.為了驗證模擬過程中能帶結構計算方法的正確性,計算了四方晶系(TET)SnO2的能帶結構,布里淵區的高對稱路徑選取為Г(0,0,0) —X(0,1/2,0) —M(1/2,1/2,0) —Г(0,0,0) —Z(0,0,1/2) —R(0,1/2 ,1/2) —A(1/2 ,1/2 ,1/2) —Z(0,0,1/2)|X(0,1/2,0) —R(0,1/2,1/2)|M(1/2 ,1/2,0) —A(1/2,1/2,1/2).結果與文獻[33]一致,能帶結構計算結果見圖A2.

表A2 平衡態α-Fe的晶格常數、原子體積和磁矩Table A2.The lattice constant,atomic volume,and magnetic moment of equilibrium α-Fe(BCC).

圖A2 SnO2 能帶結構圖Fig.A2.SnO2 band structure diagram.

本文通過改變晶格常數c或剪切角γ來模擬應變作用.首先設置了切割方向和厚度,將超晶胞結構在三個結晶方向上擴展兩個單元.然后在切割面上添加0 ?的真空層,并沿設定方向對超胞施加三種不同類型的應變載荷.垂直于應變方向和原子位置的晶格矢量同時松弛以獲得平衡結構.將應變逐步增加到5%并重復上述過程.