高斯色噪聲激勵下非對稱雙穩耦合網絡系統的隨機共振*

王燁花 何美娟

(蘭州交通大學數理學院,蘭州 730070)

研究了高斯色噪聲和周期信號共同作用下非對稱雙穩耦合網絡系統的協同效應.此系統是由大量振蕩器組成的網絡模型,個體與個體之間的相互運作、變化產生出復雜的非線性行為模式.為了進行深入研究,首先,運用平均場理論、統一色噪聲近似理論和等效非線性化等方法對原始 N 維系統進行降維近似.其次,借助役使原理得到簡化模型的郎之萬方程,進一步根據兩態模型理論推導出信噪比的理論表達式,基于此發現系統產生了尺度隨機共振現象.最后,分析了高斯色噪聲、系統參數和周期信號等對非對稱耦合網絡系統隨機共振行為的影響.結果表明,高斯色噪聲自關聯時間和噪聲強度的增大,能夠促進尺度隨機共振現象;選取合適的耦合系數能使系統隨機共振效應達到最佳.此外,還比較了高斯色噪聲和高斯白噪聲分別驅動下系統的隨機共振問題,發現高斯色噪聲更有利于增強隨機共振現象.

1 引言

1981 年,學者Benzi 等[1]模擬地球大約以10 萬年的冰川期和相對溫暖期之間交替標志著隨機共振的出現.此概念被引入后,掀起了科學家研究隨機共振的熱潮.McNamara 等[2]在1989 年將絕熱近似理論運用于雙穩系統兩態模型的研究;之后,著名學者 Dykman 等[3]利用線性響應理論描述了過阻尼雙穩系統的隨機共振現象;Zhou 等[4]提出了駐留時間分布理論.隨著隨機共振理論和方法的逐漸成熟,其被廣泛應用于各個領域,如基因調控[5]、化學突觸[6]、故障診斷[7]等,且隨機共振在越來越多的系統中被發現.靳艷飛和李貝[8]在分段非線性模型中發現存在傳統和真實兩種隨機共振現象;張曉燕等[9]在噪聲誘導的雙穩系統中發現不僅產生了單隨機共振,還出現了多重隨機共振;H?nggi 等[10]研究過阻尼系統時證實高斯色噪聲會削弱隨機共振效應;焦尚彬等[11]探究了α穩定噪聲與時滯項結合下單穩系統的共振問題,仿真表明時滯項不影響隨機共振的產生.隨機共振的發生不僅與系統、噪聲有緊密聯系,還和信號密不可分.Zhang 和Zheng[12]研究了周期矩形信號和高斯色噪聲共同作用下的時滯雙穩系統,發現系統產生了多重隨機共振現象.楊建華等[13]討論了受二進制非周期信號和周期方波信號激勵的分數階雙穩系統的非周期振動共振問題,并將其應用于檢測微弱信號.俞瑩丹等[14]對正弦信號和高斯白噪聲協同作用下四穩系統進行分析,證實系統存在著雙重隨機共振現象.

在隨機共振的研究過程中,大多是針對單個變量的一維系統,而在實際現實中,事物之間往往是相互關聯的,表現出復雜的動力行為,并不是孤立、單一的.因此,更能描述實際問題的耦合網絡系統受到越來越多的關注和研究.如馬圣楠[15]討論了耦合網絡的捕食系統的復雜行為,對生態學的發展具有重要的意義;何傳磊[16]研究了軌道交通網絡,分析網絡之間的耦合協調度以提高交通網絡的安全性;劉小強[17]分析了耦合時滯和電磁感應共同作用下神經元網絡的隨機共振行為,在醫學領域為提高患者感知能力提供了一種思路;孫中奎等[18]對高斯白噪聲作用下非對稱雙穩耦合網絡系統進行探索.然而,對于網絡系統動力學行為的研究,大多數成果集中在高斯白噪聲上.由于高斯白噪聲的產生需要提供無窮大的功率,這是無法實現的,屬于一個理想情形.具有有限功率的高斯色噪聲更符合實際需要,且能夠更好地闡述客觀實際,會使相關研究更具現實意義,故研究具有關聯時間的高斯色噪聲誘導下耦合網絡系統的動力學現象雖然復雜,卻更有必要.

本文研究了高斯色噪聲與周期信號共同作用下非對稱雙穩耦合網絡系統的隨機共振(stochastic resonance,SR)現象.考慮到原系統的復雜性和非線性,首先對原始模型進行降維處理,之后求得簡化模型的郎之萬方程,在絕熱近似條件下,計算出信噪比(signal-to-noise ratio,SNR)的理論表達式,并發現系統存在尺度隨機共振現象;最后分別討論系統隨機共振行為隨著高斯色噪聲自關聯時間、噪聲強度、耦合系數、非對稱性系數、周期信號幅值等參數變化而不同的演化情況.

2 非對稱雙穩耦合網絡系統

本文考慮一組由N個相互作用的雙穩態振蕩器組成的模型[19],其中每一個xi都是單自由度的,同時受到高斯色噪聲和周期信號的共同作用,可用如下隨機微分方程表示:

其中i=1,2,···,N;r是非對稱性系數;N是系統尺度;θ定義為振蕩器之間相互作用的耦合參數;ηi(t)是自關聯時間為τ、噪聲強度為D的高斯色噪聲,且滿足性質

周期信號S(t)=Acos(ωt),A是信號幅值,ω是信號頻率.

將系統(1)看作一個整體,定義xi的全局變量階波動矩

對于(1)式分別運用平均場理論[20]和 It隨機微分法則[21]降維可得關于X與Mk(t)的隨機微分方程為

由于方程(2)和方程(3)具有non-Markovian,基于統一色噪聲近似原理[22,23],簡化可得如下模型:

其中c(X)=X ?M3?3M2X ?3M1X2?X3+r+S(t);c′(X) 是關于X的導數;ξ(t)為高斯白噪聲,且滿足性質

d′(X)是關于X的導數;ζ(t)為高斯白噪聲,且滿足〈ζ(t)〉=0,〈ζ(t)ζ(t′)〉=2Dδ(t ?t′) .

進一步,對(4)式與(5)式的非線性函數進行等效線性化,令

將(4)式和(5)式在X=0 處泰勒展開,得到近似模型:

依據Kn與Mn的關系,可得X和K2的隨機微分方程:

運用高斯近似[24]和役使原理[25],化簡(8)式與(9)式得到Langevin 方程:

令V ′(X)=0,計算得到方程(10)的兩個穩定點為

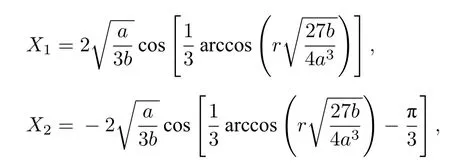
一個不穩定點為

3 信噪比

隨機共振是一種噪聲對于微弱信號起到協助并促進輸出作用的非線性現象.目前,衡量隨機共振的測度指標主要有信噪比、信噪比增益、駐留時間分布、互相關系數、統計復雜度等.對于信噪比這一指標傾向于體現出輸入或輸出信號的特性,故本文采用信噪比來反映系統發生隨機共振的效果.信噪比 SNR 定義為功率譜中信號特征頻率處的幅值與噪聲之間的比值,公式如下:

式中,SS(ω)和SN(ω) 分別表示信號和噪聲功率譜密度.

接下來推導系統(10)的信噪比表達式.

利用Novikov 定理[26]等經典理論,得到方程(10)的近似FPK 方程如下:

根據平均首通時間的概念和最速下降法[27,28],可得粒子分別由X1和X2所在勢阱的逃逸速率±為

運用兩態模型理論[29],關于±小參數Acos(ωt)展開取到A的一次項為

在絕熱近似條件[30]下,兩勢阱的總概率量n±滿足如下方程:

由于絕熱近似要求振幅A ?1,略掉A的二次項之后,得到信噪比表達式為

4 隨機共振

接下來,基于信噪比理論表達式(15)對高斯色噪聲和周期信號共同作用下耦合網絡系統隨機共振行為隨色噪聲參數、系統參數和周期信號等參數的變化情況進行詳細討論.

4.1 隨機共振的產生

信噪比 SNR 作為高斯色噪聲強度D的函數,其演化情形如圖1 所示,其他參數固定為N=3,θ=2,τ=0.15,A=0.01,r=0.01 時,從 圖1 可以發現,隨著噪聲強度D從0 逐漸增大到1,SNR曲線先逐漸增大后減小,出現了單峰狀態,由此表明系統產生了隨機共振現象.

圖1 SNR 關于噪聲強度D的演化圖Fig.1.Evolution of SNR with noise intensity D.

4.2 高斯色噪聲對隨機共振的影響

本小節研究高斯色噪聲自關聯時間τ和噪聲強度D對系統(10)隨機共振響應的影響.圖2 描述了 SNR 作為系統尺度N的函數隨著自關聯時間τ變化的演化情況.從圖2 可以得出,當其他參數選取為θ=3,D=0.3,A=0.01,r=0.02 時,每一條 SNR 曲線隨著N的增加都呈現出非單調的演化趨勢,即在某個N值處產生明顯的峰值,意味著系統出現了尺度隨機共振現象;進一步,隨著τ從0.05 逐漸增大到0.4,可以發現 SNR 曲線的峰值逐漸增大,且位置向右發生偏移,峰值對應的系統尺度N也從4 變化到6,說明τ的增大能夠促進尺度隨機共振的產生.

圖2 SNR 作為系統尺度N的函數關于不同自關聯時間τ的關系圖Fig.2.Relationship of SNR as a function of system scale N with different correlation time τ .

圖3 給出了 SNR 在不同系統尺度N的條件下,隨著輸入噪聲強度D的改變而產生的不同輸出情況.從圖3(a)可以觀察到,針對每一個噪聲強度D,SNR曲線伴隨著N的增加都呈現出單峰狀,說明原始系統出現了 SR 現象.當其他參數為θ=3,τ=0.1,A=0.01,r=0.02 時,隨 著D從0.17 變化到0.5,SNR的峰值逐漸增大,峰值所對應的N值向右移動,表明噪聲強度D的增大能夠增強 SR 現象.

為了比較高斯色噪聲與高斯白噪聲對于非對稱耦合網絡系統 SR 行為的影響,取定參數為θ=4,τ=0.1,A=0.01,r=0.03 時圖3(b)給出兩種噪聲分別誘導下系統 SNR的演化圖形,其中粉色曲線表示高斯色噪聲作用下 SNR的演化圖,藍色曲線表示高斯白噪聲作用下 SNR的演化圖,從圖3(b)可以看到D=0.3,D=0.5 時,高斯色噪聲驅動下系統輸出 SNR 數值均比高斯白噪聲驅動下系統輸出的SNR 數值要大.由此表明,在同一噪聲強度D下高斯色噪聲能夠增強尺度隨機共振現象.

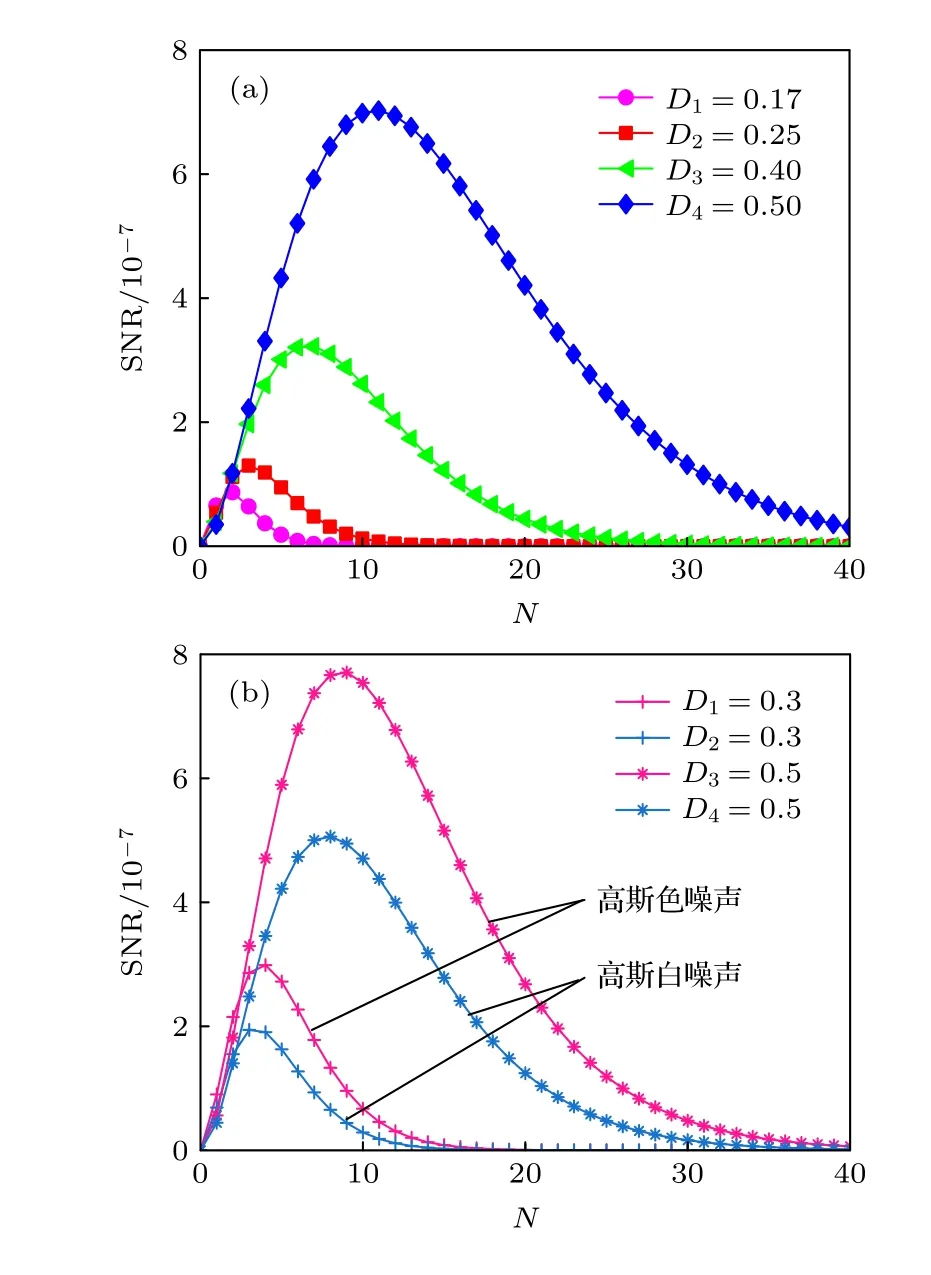
圖3 噪聲強度D 對輸出信噪比SNR的影響 (a) SNR 作為系統尺度N的函數關于D 變化的曲線;(b) 分別由高斯色噪聲、高斯白噪聲驅動下系統輸出SNR的對比Fig.3.The influence of noise intensity D on the output SNR: (a) Curve of SNR as a function of the system scale N with the change of D;(b) comparison of system output SNR driven by Gaussian colored noises and Gaussian white noises respectively.

4.3 系統參數對隨機共振的影響

為了進一步考慮系統參數的改變對隨機共振動力學行為的影響,下面給出了耦合系數、非對稱性系數和系統尺度的SNR 演化趨勢圖,結果如圖4—圖6 所示.

圖4(a)描述了系統輸出 SNR 在不同系統尺度N條件下,隨著耦合系數θ變化而發生的不同輸出情況.可以看出,對給定的θ值,每條 SNR 曲線都呈現出開始隨著D的增加而增加,之后隨著D的增大而減小的非單調演化趨勢,表明系統出現 SR 現象.另外,給定D=0.3,τ=0.1,A=0.01,r=0.02,當θ從1.85 逐漸增大到2.5 時,SNR 曲線的峰值逐漸變大,且輸出 SNR的最大值所需N向N增加的方向移動,也就是說,θ的增加可促進系統 SR的產生;但是當θ再逐漸增大至28 時,觀察到 SNR 曲線的峰值卻在減小,且 SNR的最大值所對應的N向N減小的方向移動,即較大的θ抑制了系統產生 SR .換言之,選取合適的耦合系數θ能夠使系統 SR 效應達到最佳效果.

圖4 耦合系數 θ 對輸出信噪比SNR的影響 (a) SNR 作為系統尺度N的函數關于 θ的變化曲線;(b) 分別由高斯色噪聲、高斯白噪聲驅動下系統輸出SNR的對比Fig.4.The influence of coupling coefficient θ on the output SNR: (a) Curve of SNR as a function of the system scale N with the change of θ ;(b) comparison of system output SNR driven by Gaussian colored noises and Gaussian white noises respectively.

圖4(b)分析了耦合系數對高斯色噪聲和高斯白噪聲分別誘導下系統 SR 行為的影響.固定其他參數為D=0.3,τ=0.1,A=0.01,r=0.03,無論耦合系數θ=3 還是θ=8,高斯色噪聲激勵下耦合網絡系統輸出 SNR 曲線數值均高于高斯白噪聲下SNR值.由此表明,在相同耦合系數θ下,高斯色噪聲能加強尺度隨機共振現象.

圖5 討論了 SNR 作為系統尺度N的函數隨著非對稱性系數r變化的演化趨勢.可以觀察到,隨著N的增大,每條 SNR 曲線都出現了共振峰,即系統出現了 SR 現象.當θ=3,D=0.3,τ=0.1,A=0.01時,隨著r從0.03 變化到0.1 時,SNR 曲線峰值的高度明顯上升.又注意到,在r=0.03 和r=0.05時 SNR 峰值對應系統尺度N=4,而r=0.07與r=0.1 處峰值對應的N=3 保持不變,換句話說,非對稱性系數r對高斯色噪聲作用下系統尺度隨機共振的影響是緩慢變化的.

圖5 SNR 作為系統尺度N的函數關于不同非對稱性系數r的關系圖Fig.5.Relationship of SNR as a function of system scale N with different asymmetric coefficient r.

系統信噪比 SNR 在不同噪聲強度D條件下,隨著系統尺度N變化而發生的不同輸出情況如圖6 所示.可以觀察到,當N分別取4,8,12 和16 時,每條 SNR 曲線都出現了單峰,說明系統產生了 SR 現象.詳細地說,選取參數為θ=2,r=0.02,τ=0.5,A=0.01 時,隨著N從4 逐漸增加到16,系統輸出 SNR 與N的增大成正比,當N取到16時,隨機共振的效果更顯著,這一結果表明增大系統尺度N能夠促進系統的SR 現象.

圖6 SNR 作為噪聲強度D的函數關于不同系統尺度N的關系圖Fig.6.Relationship of SNR as a function of noise intensity D with different system scale N.

4.4 周期信號對系統隨機共振的影響

本節討論余弦信號S(t)=Acos(ωt) 對耦合網絡系統隨機共振行為的影響.圖7 給出了信噪比SNR作為系統尺度N的函數,當周期信號振幅A變化時的演化趨勢.從圖7 中可以得到,每條SNR曲線都有先增加后減小的變化趨勢,都存在局部最大值,說明系統出現了 SR 現象.具體來看,當給定其他參數為θ=3,D=0.3,τ=0.1,r=0.02 時,A從0.02 逐步增大到0.15 時,SNR 曲線的峰值高度隨之變高.這表明,信號振幅A的增大能夠使系統 SR 效應更加強烈.

圖7 SNR 作為系統尺度N的函數關于不同周期信號振幅A的關系圖Fig.7.Relationship of SNR as a function of system scale N with different periodic signal amplitude A.

5 結論

本文研究了高斯色噪聲與周期信號共同驅動下非對稱雙穩耦合網絡系統的隨機共振現象.由于采用的模型是N維系統,直接研究比較困難且具有較強的非線性,故先運用平均場理論和統一色噪聲近似原理將高斯色噪聲誘導下的non-Markovian模型進行降維近似,再通過等效線性化得到簡化模型,之后根據高斯近似和役使原理化簡得到等價的Langevin 方程,最后在絕熱近似條件下,利用經典隨機共振理論,推導出包含所有參數的輸出信噪比函數關系式.

結果表明,在一定的參數范圍內,系統出現了隨機共振現象.高斯色噪聲自關聯時間、噪聲強度的增加能夠促進尺度隨機共振的產生;非對稱性參數的增大,抑制了隨機共振效果;而選取合適的耦合系數使系統的輸出響應達到最大.另外,信號幅值的改變不會影響系統產生隨機共振的尺度.此外,還對比分析了在其他參數一致的前提下,高斯色噪聲和高斯白噪聲分別激勵下系統的隨機共振行為.研究發現,高斯色噪聲作用下耦合網絡系統輸出信噪比的數值更大,高斯色噪聲較高斯白噪聲更有利于增強系統隨機共振現象.