不同光學網絡結構玻色采樣發生隨機光子損失的模擬研究*

季陽 陳美玲 黃汛 吳永政 蘭冰

(中國電子科技集團公司第三十二研究所,上海 201808)

玻色采樣機是最有可能真正意義上實現量子優勢的專用量子計算機之一,其在量子化學等領域也有著很好的應用前景.然而,光子損失相關的噪聲會引起玻色采樣樣本的誤差.為了研究光子損失對玻色采樣的影響,基于等效分束器原理,對玻色采樣展開經典的模擬研究.對于對應任意幺正矩陣的兩種光學網絡,當在每一個光學單元中有一定概率發生光子損失時,發現具有Clements 結構光學網絡的玻色采樣相比于Reck 結構的樣本誤差更小.進一步地,當光子損失的概率符合正態分布時,發現若光子損失概率平均值不變,標準差越大,玻色采樣的樣本誤差越大.最后,考慮輸出光子數的實驗結果表明,隨著光子損失概率的提高,無光子損失的輸出組合比例急劇下降,說明光子損失會明顯影響玻色采樣的量子優勢.隨機光子損失的玻色采樣模擬研究有助于玻色采樣實驗的開展,為含噪聲量子計算研究提供思路.

1 引言

量子計算機在解決某些復雜問題,如大數分解問題[1]、搜索問題[2]時相比于經典計算機具有指數級加速的潛力,因此吸引了越來越多的關注.但受限于目前的技術手段,具有大規模以及高保真度的通用量子計算機仍然難以在短時間內實現.基于此,研究專用量子計算機具有很強的現實意義.這主要是因為,專用量子計算機可以率先實現真正意義上的量子優勢,即量子計算機在解決某些高復雜度問題上相比傳統計算機具有明顯的加速效果.

玻色采樣機作為一種專用量子計算機,由于其具有結構簡單、類型多樣[3-6]、可以通過多種手段實現[3,7]、不需要量子邏輯門[8]、經典驗證方法成熟[9-11]等優勢,是近年來量子計算領域的研究熱點之一.玻色采樣概念的提出是為了在計算復雜度問題上推翻廣義“丘奇-圖靈”論題[8],這一目標隨著2020年的76 光子100 模式高斯玻色采樣實驗的開展已基本實現[4].除此之外,在超導量子線路上進行的玻色采樣也成功模擬了分子振動譜[12],這說明玻色采樣在量子化學領域也具有很好的應用前景.

但是,玻色采樣的超大規模實現始終面臨著一些困難,主要有光子非全同和光子損失.當光子非全同和光子損失所引起的噪聲足夠明顯時,玻色采樣的樣本可以由經典算法在多項式時間內模擬得到,此時玻色采樣機失去了量子優勢[13].因此,對光子非全同和光子損失的研究具有重要意義.光子非全同指的是光子在某一個內在量子態上存在差異,例如光子的頻率或者位置.人們通過一系列理論研究,得到了光子非全同的玻色采樣輸出組合概率及對應的高效經典估算方法[14,15].在實驗方面,相比于傳統的自發參量下轉換,后來發展的光學微腔-半導體量子點體系制備出來的光子全同度更高,更加適合大規模實現典型玻色采樣[16].

同時,研究者們也對光子損失玻色采樣的理論和實驗開展了深入的研究.光子損失是指光子在產生、傳輸、探測過程中發生丟失的情況,其與光子源、光學網絡、探測器的質量密切相關.與光子非全同一樣,光子損失會明顯影響玻色采樣的量子優勢.對于光子損失對玻色采樣量子優勢影響的分析,主要基于兩種理論模型.一種模型是對輸出端損失光子的個數進行統計分析.例如,對于輸入光子數為n,輸出光子數為(n?l):若l為一個常數,則玻色采樣仍然具有量子優勢;若則玻色采樣失去量子優勢[17].更一般地,隨著輸入光子數的增加: 若損失光子數與輸入光子數之比趨向于0,則玻色采樣仍然具有量子優勢;若損失光子數與輸入光子數之比趨向于1,則玻色采樣失去量子優勢[13].第二種模型則是考慮光子損失有可能發生在每一個光學元件中,其更加符合實際實驗模型[18].這種模型將光子損失等效為光子通過一個虛構的分束器進入到環境光路中.基于此,對光子損失的玻色采樣模擬實際上等效于對更大規模光學網絡的玻色采樣模擬.這種模型揭示了光子損失玻色采樣的量子優勢與光學網絡的深度密切相關[17].

本工作基于光子損失情況下玻色采樣的第二種理論模型展開,對不同結構的光學網絡模型進行了定量的分析,給出了直觀的比較結果.同時本文的模擬結果由于考慮了光子損失概率的隨機性,更加符合真實物理場景.

2 模 型

2.1 理論模型

目前比較常用的兩種光學線性網絡,即Reck結構和Clements 結構的光學網絡,如圖1 所示,圖中每一個交點都表示一個光學單元.

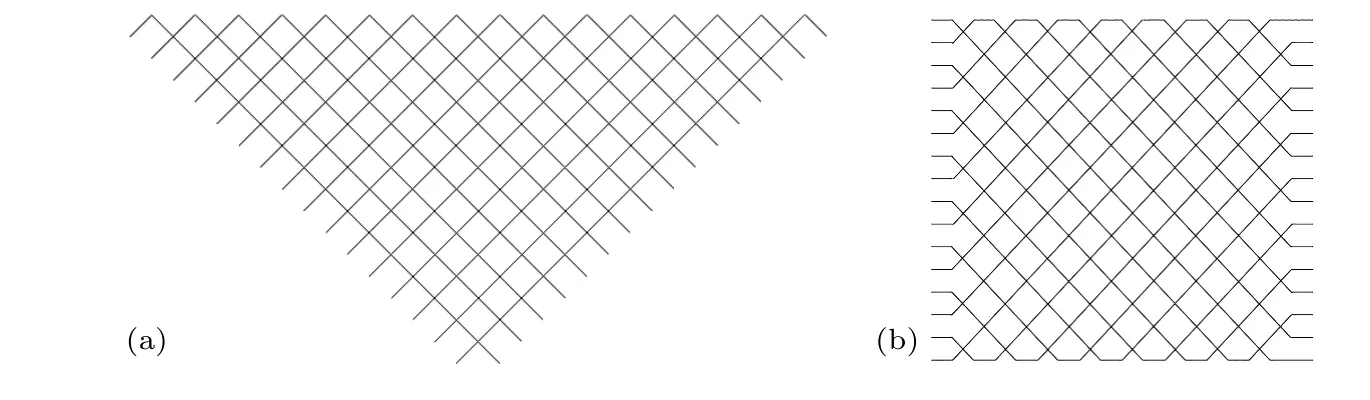
圖1 光學線性網絡示意圖: (a) Reck 結構;(b) Clements 結構Fig.1.Sketches of optical linear networks: (a) the Reck structure;(b) the Clements structure.

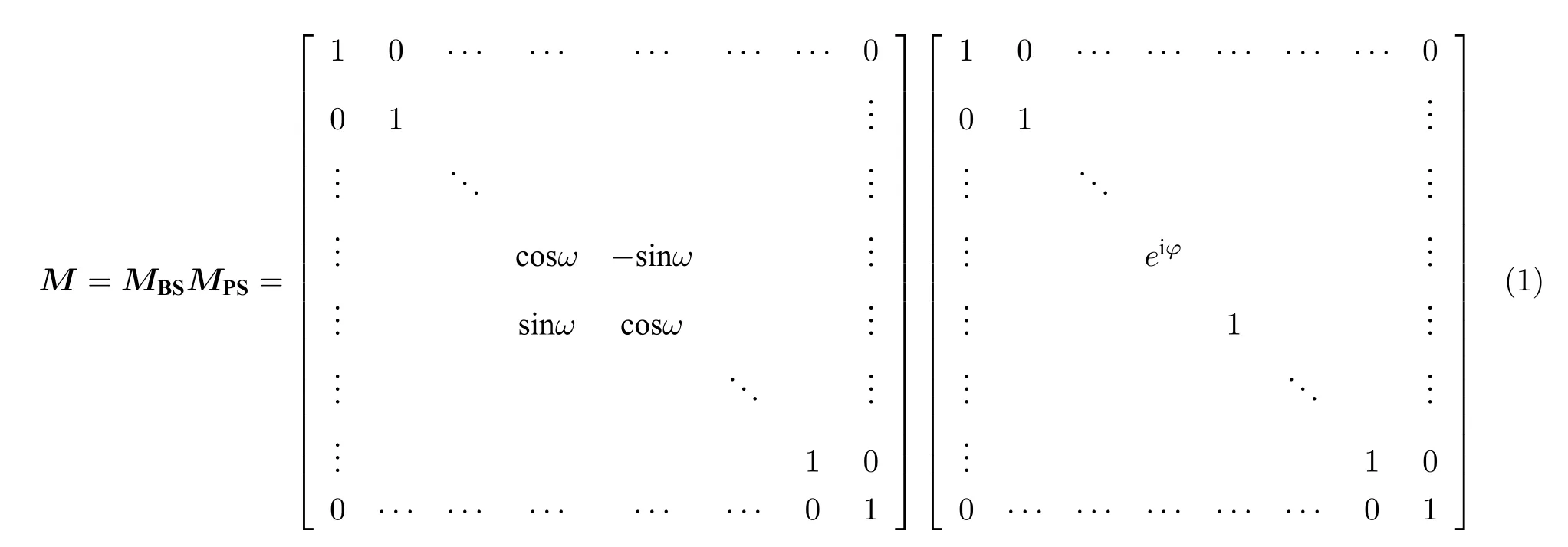
其中,Reck 結構為三角形非對稱結構,而Clements 結構為四邊形對稱結構[19].直接對任意m維幺正矩陣進行分解,使其可以表示為一系列矩陣相乘的形式.在該系列矩陣中,第一個矩陣是對角矩陣,對應光學網絡末端的m個相移器;其余矩陣均對應一個光學單元,每個光學單元由一個相移器和一個分束器組成.每個光學單元對應的幺正矩陣M可以表示為分束器矩陣MBS和相移器矩陣MPS的乘積[19]:其中分束器的反射率是cosω,相移器改變的相位是φ,分束器矩陣含參元素所在行(列)數為分束器所在的兩個通道數,相移器矩陣含參元素所在行(列)數為相移器所在的通道數.

2.2 實驗

對于任意的幺正矩陣U,將其分解成一系列矩陣相乘的形式,該系列矩陣對應的光學單元的排列符合Reck 結構,其分解方法如算法1 所示[20].

對于Clements 結構,U的分解方法如算法2所示[19].Clements 結構的光學網絡對應的矩陣構造方法要比Reck 結構復雜得多.這主要是因為,U需要交替右乘和左乘一系列矩陣來實現對角化,即MM···MUM?1M?1···M?1=D,其 中D為對角矩陣,M表示一系列參數(通道數,反射率以及相位)不盡相同的光學單元矩陣,則U可以表示為形如M?1M?1···M?1DMM···M的形式.在此基礎上,可以初始化一個對角矩陣D'以及一個光學單元矩陣M',使得D′M′=M?1D.經過計算可以發現,D'和M'的參數是唯一的,則U可以表示為形如M-1M-1···M-1D'M'MM···M的形式,此時該形式中對角矩陣左乘的矩陣減少1 個,而右乘的矩陣增加1 個.通過重復構造D'和M',最終U可以表示為形如D'M'M'···M'MM···M的形式,實現基于Clements 結構對U的分解.

在得到對應任意幺正矩陣的光學網絡后,為了研究在光學網絡中發生的光子損失對玻色采樣的影響,基于等效分束器原理對光學網絡進行重構.2 個虛構的分束器和2 條環境光路被加入每個光學單元中.虛構的分束器參數ω和單條實際光路在單個光學單元中的光子損失概率Ploss滿足cosω=1 — (1 —Ploss)1/2關系[18].當光子在該光學單元中發生損失,則其等效于光子通過虛構的分束器進入環境光路中.由于兩種光學網絡都具有m(m— 1)/2個光學單元,在重構的光學網絡中,一共附加了m(m— 1)個虛構分束器和相同數目的環境光路,則重構的光學網絡的模式數變為m2,因此原始m維矩陣M需要變換為m2維矩陣,即M⊕Em(m—1),其中Em(m—1)為m(m— 1)維單位矩陣.相應地,虛構的分束器矩陣也是m2維矩陣.在得到重構后的光學網絡后,則可以計算考慮光子損失的玻色采樣輸出組合概率,其方法如算法3 所示,在計算輸出組合概率的過程中,需要計算矩陣的積和式,可以采用Ryser 或者Glynn 方法,并利用格雷碼以簡化計算過程[21].計算了4 光子16 模式的玻色采樣輸出組合概率,其中16 維輸入組合S=[1,1,1,1,0,0,···,0].一共隨機產生了100 個16 維隨機幺正矩陣,并對最終計算結果取平均值.

3 實驗結果及討論

基于玻色子生日悖論,在只考慮輸出組合中每個通道只有0 或1 個光子的情況時,可以通過總變差距離來評估玻色采樣的輸出結果與理想情況的偏差程度[21].總變差距離可以表示為Pideal|,其中T4表示沒有發生光子損失的任意16維輸出組合,Pideal表示理想情況下歸一化的輸出組合概率.為了便于與理想情況對比,Pout也需要進行歸一化處理,使得對于所有的T4,Pout之和為1.如圖2(a)所示,我們發現隨著光子損失概率的提高,總變差距離以準線性的方式逐步變大,這表明光子損失會對玻色采樣的精度產生顯著影響.我們可以直觀地發現,對于固定的Ploss,Clements結構比Reck 結構對應的總變差距離更小,表明Clements 結構在光子損失情況下穩定性更好.這主要是因為Clements 結構受到平衡與非平衡光子損失的影響更小[19].在光子損失情況下,一方面,對于平衡光子損失,光學網絡深度越大,光子損失程度越高.對于較大規模光學網絡,Clements 結構的深度比Reck 結構小很多,因此受到平衡光子損失的影響更小;另一方面,對于非平衡光子損失,光子損失程度與通道中分束器的光子損失概率密切相關.在Reck 結構中,由于每個通道經過的分束器數目不同,導致通道中光子損失程度不同,這極大地影響了多光子相干干涉結果.而在Clements結構中,每個通道經過的分束器數目大致相同,通道中光子損失程度大致相當,因此在Clements 結構中非平衡光子損失對多光子相干干涉結果的影響相比于Reck 結構較小.

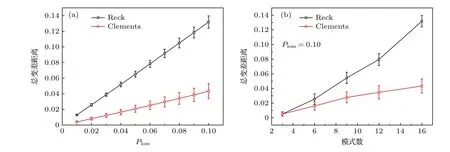
圖2 (a) 考慮光子損失的玻色采樣輸出組合概率的總變差距離隨光子損失概率Ploss的變化關系;(b) Ploss為0.1 時,兩種光學網絡結構隨著模式數增加對應玻色采樣結果總變差距離的變化關系.圖中空心圖形代表實驗結果平均值,誤差棒代表標準差Fig.2.Plots between the total variation distance of boson sampling output combination probabilities considering photon losses and(a) the photon loss probability Ploss or (b) mode numbers when Ploss is 0.1.Open shapes represent mean values and error bars represent standard deviations.

為了驗證上述結論,我們對不同規模的玻色采樣進行了仿真,如圖2(b)所示,所采用玻色采樣規模分別為1 光子3 模式、2 光子6 模式、3 光子9 模式、3 光子12 模式和4 光子16 模式.在模式數為3 時,兩種結構具有同樣的形式,因此總變差距離相同.隨著模式數的增加,光學網絡深度增加,通道經過的最大分束器數目增加,導致兩種結構對應的總變差距離也逐漸增加,表明光子損失(包括平衡與非平衡光子損失)對玻色采樣結果的影響逐漸加大.而Reck 結構對應的總變差距離增幅明顯高于Clements 結構,表明Clements 結構受到平衡與非平衡光子損失的影響相對于Reck 結構更小.

進一步假設每個光學單元對應的Ploss不是一個定值,而是符合一定的隨機分布,即正態分布.可認為這樣的假設比較能夠反映出真實的物理實驗情況.分兩種情況進行了模擬: 第1 種情況是,固定Ploss的標準差不變,改變其平均值.對于這種情況,發現總變差距離的變化情況與圖2(a)類似;第2 種情況是,固定Ploss的平均值不變,改變其標準差.研究發現,對于兩種光學網絡結構,隨著Ploss標準差的增大,輸出組合概率的總變差距離呈現變大的趨勢,如圖3 所示,表明光子損失概率的離散程度也會明顯影響玻色采樣的精度.以深度為3的光學網絡為例,對這種情況進行簡單的分析.此時光學網絡的每一層只含有一個光學單元.在Ploss為一個定值P時,每一層的光子透過率為T=1 —P,因此總光子透過率是T3.若Ploss符合平均值為P的正態分布,則每一層的光子透過率也符合平均值為T的正態分布,總光子透過率的期望值仍為T3.為了滿足這個條件,隨著Ploss標準差的增加,總光子透過率小于T3的概率需要逐漸增加.受較低的總光子透過率的影響,輸出組合概率的總變差距離相應增加,表明光子損失對玻色采樣精度的影響變得更為顯著.

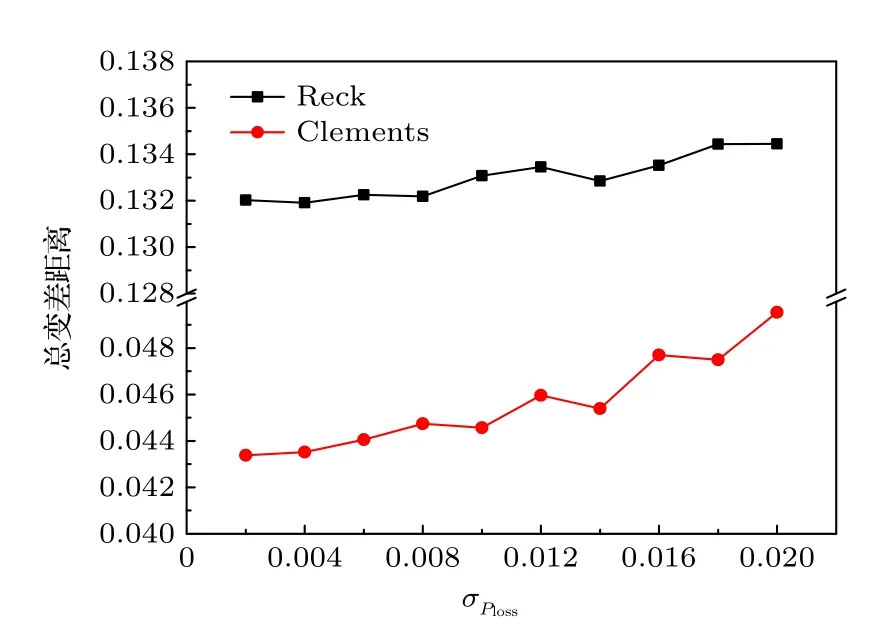
圖3 考慮光子損失的玻色采樣輸出組合概率的總變差距離平均值隨光子損失概率的標準差σPloss的變化關系Fig.3.Plots between the mean values of total variation distance of boson sampling output combination probabilities considering photon losses and the standard deviation σPloss of photon loss probability.

最后,統計了固定光子個數的輸出組合的概率之和隨著光子損失概率變化的情況,如圖4 所示.當Ploss=0.01 時,Clements 結構相比于Reck 結構,4 光子輸出的概率明顯較高.由于輸出光子數越高,其對應的經典計算的時間復雜度也越高,我們的結果表明在光子損失情況下,Clements 結構的玻色采樣對于經典計算來說具有更高的時間復雜度.而隨著Ploss的提高,4 光子輸出概率急劇減小,3 光子輸出占據優勢.進一步提高Ploss,則2 光子輸出變成主導.這表明,發生在光學網絡中的光子損失能夠顯著地影響玻色采樣的量子優勢.當低光子數的輸出組合占據主導時,玻色采樣變得易于被經典算法模擬,如MCMC 算法[22]、Clifford-Clifford 算法[23]等.

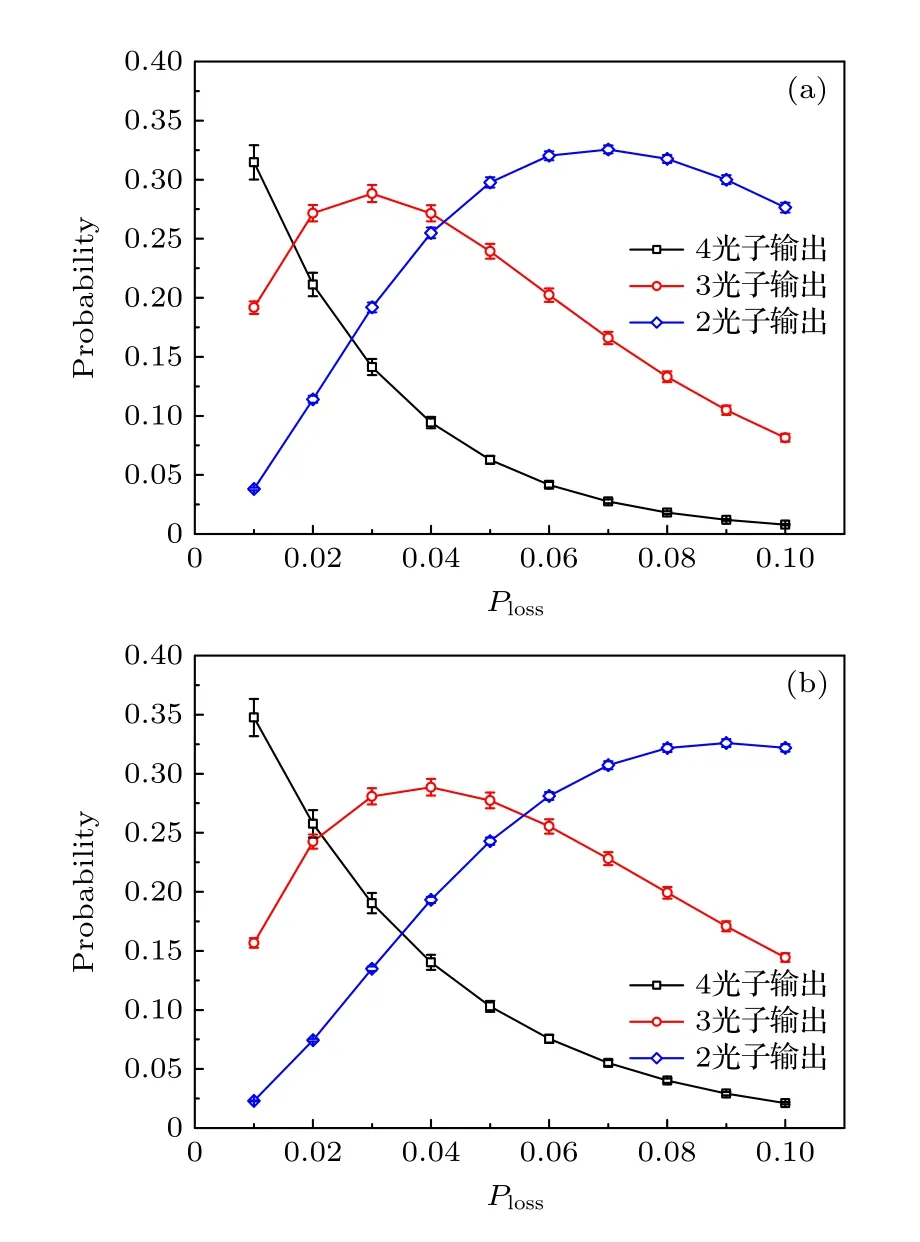
圖4 玻色采樣固定光子個數的輸出組合概率之和隨著Ploss的變化關系.(a) Reck結構;(b) Clements 結構光 學網絡.圖中空心圖形代表實驗結果平均值,誤差棒代表標準差Fig.4.Plots between the sum of boson sampling output combination probabilities with fixed photon numbers and Ploss: (a) the Reck structure;(b) the Clements structure.Open shapes represent mean values and error bars represent standard deviations.

基于對光子損失情況下玻色采樣的經典仿真結果,發現光子損失能夠顯著影響玻色采樣結果的精度,進而影響玻色采樣量子優勢的可實現性.如何抑制光子損失對玻色采樣機等光量子器件的影響一直是研究熱點之一.在理論方面,系統研究了輸出光子個數[24]、光學網絡深度[17]等對玻色采樣對應經典計算時間復雜度的影響.在工程技術方面,減反射涂層[16]、光路拓展[25]、三維光學網絡[26]的應用提供了抑制光子損失影響的可能性.值得一提的是,在容錯全光量子中繼器方案中,利用量子奇偶碼有效抑制了光子損失的影響,這給未來光量子計算器件抵抗光子損失帶來了啟示[27].

4 結論

系統研究了兩種結構的光學網絡中光子損失對玻色采樣的影響.可以直觀地發現,當存在光子損失時,Clements 結構相比于Reck 結構具有更好的穩定性,其輸出高光子個數的概率更高,對應經典計算的時間復雜度更高.隨著光子損失概率的提高,玻色采樣的精度明顯降低,且輸出高光子個數的概率急劇降低,表明光子損失對玻色采樣的經典計算時間復雜度具有十分顯著的影響.研究還發現,若光學單元中光子損失概率不是一個定值,而是服從正態分布,則光子損失概率的離散程度也能夠影響玻色采樣的精度.結果表明,發生在光學網絡中的光子損失能夠明顯影響玻色采樣的精度和對應經典計算的時間復雜度,這對真正意義上具有量子優勢的玻色采樣的物理實現提出了又一個挑戰.