uBlock類結構最優向量置換的高效搜索

李曉丹 吳文玲 張 麗

1(中國科學院軟件研究所可信計算與信息保障實驗室 北京 100190) 2(中國科學院大學 北京 100049) 3(中國星網網絡系統研究院有限公司 北京 100083)

在分組密碼的設計和分析中，整體結構是首要的研究對象.作為分組密碼的重要特征，整體結構對于分組密碼的輪數選取、軟硬件實現性能都有非常大的影響.常用的分組密碼整體結構有：Feistel結構、SP結構、廣義Feistel結構、MISTY結構、Lai-Massey結構以及由上述結構彼此嵌套形成的細化整體結構.其中，SP結構非常清晰，是直接基于香農的“混淆”和“擴散”原則實現的整體結構，通常包含一個可逆的非線性函數S和一個可逆線性變換P，其中S層起混淆作用，線性層P起擴散作用.當給定S層和P層的某些密碼指標，設計者可給出SP密碼抵抗差分分析和線性分析的可證明安全.相較于Feistel結構，SP結構擴散速度更快，但是為達到加密和解密的相似性需要合理設計密碼部件.SP結構的分組密碼算法有：AES[1],ARIA[2]和Serpent等.其中AES無疑是目前最重要的分組密碼，它的擴散層由2部分組成，也被稱為兩級擴散層，一部分是選取分支數最大的MDS矩陣作為列混淆，另一部分是行移位操作.特別地，許多分組密碼和雜湊函數的設計都是從AES的初始設計結構開始，對一個或多個部件進行調整以滿足其設計要求，如Anubis[3]，LED[4]，Midori[5]，PHOTON[6]，QARMA[7]，SKINNY[8]和Whirlpool[9].此類算法的線性層本身由2部分組成:一部分類似于AES的列混合操作，另一部分類似于AES行移位操作，我們稱這類密碼算法為類AES密碼算法.列混合操作是對狀態列的矩陣乘法，行移位操作是對狀態字的置換.對于前者，研究結果較多，只需要保證其具有高的分支數，分支數越高，對應的活躍S盒數越多，則抵抗差分分析和線性分析的能力越強.AES選取的列混合操作為分支數最大的MDS矩陣，而出于輕量化考慮的一些算法，如Midori，SKINNY等，則采用非最優分支數的二元矩陣.而對于字換位操作，當僅考慮超過2輪的情形時，字換位的選取極大影響活躍S盒的數量，因此，對于好的設計來說，精心選擇字換位操作至關重要.對于AES，得益于寬軌跡設計策略[10]，可以獲得數學上可證明的最小活躍S盒數的界限，保證4輪后至少有25個活躍S盒.Midori算法設計的初衷是減少硬件資源損耗，它采用類似于AES算法的結構，與SKINNY算法類似，它們都屬于類AES算法，但是在列混淆部分選用非最優分支數的矩陣.Midori設計者發現使用分支數為4的二元矩陣時，4輪后活躍S盒數下降到16個，但改變字換位操作可顯著提高活躍S盒數.2015年，文獻[11]證明了對于選用最優分支數的列混合操作的算法，用任意置換替換字換位操作不能增加活躍S盒的數量.2016年，文獻[12]給出，用B表示矩陣的分支數，對于經典字換位操作，則對于列混合為MDS矩陣的，4輪后至少有B2個活躍S盒；對于列混合為二元矩陣的，4輪后活躍S盒的下界可能大于B2，且對于某些二元矩陣，下界可達到B(B+2).2018年，文獻[13]提出一種加速搜索字換位操作的技術，并應用于Midori和SKINNY算法，尋找使得整體擴散性更好的字換位操作.這也是現在輕量級分組密碼的一個設計趨勢，擴散層選擇非MDS矩陣，雖然擴散效果沒有MDS矩陣好，但是實現效率會有很大提高,這在資源受限的環境下有很大優勢，而且在結合合適的向量置換操作后，整體算法也可以達到較好的擴散性和安全性.因此，使用類AES結構來設計輕量級分組密碼是一個不錯的選擇，特別是列混合操作選用最優二元擴散層,并結合恰當的向量置換，可以很好地平衡安全性和實現代價，然而在選定列混合操作后，搜索合適的向量置換并不容易，這也是這類算法在設計時需要花費大量精力的部分.

uBlock算法[14]是全國密碼算法設計競賽中的獲勝算法.該算法是經典的SP結構，是一種典型的類AES算法，線性層選用的是16維的最優二元擴散層與向量置換的組合，擴散速度快且可以在各種軟硬件平臺上高速實現.受文獻[13]的啟發，本文研究了uBlock類結構的擴散性，并給出了尋找最優置換的搜索策略.通過對uBlock類結構中二元擴散層性質的研究，我們給出uBlock類結構全擴散輪數的下界.根據結構特點，我們揭示了uBlock類結構等價類的劃分準則，并基于此給出了uBlock類結構最優向量置換的搜索策略.最后根據128 b和256 b分組的uBlock類結構的特點，進一步優化了搜索策略，并依據全擴散輪數、性能和超級擴散層的分支數3個指標，給出了128 b和256 b分組的uBlock類結構的一系列最優向量置換.我們的方法可以大幅度降低需要測試的置換對，為后續uBlock類算法的設計提供技術支持.

1 基礎知識

本節介紹相關的基礎概念和定義.

1.1 符號表示

表1給出了本文中使用的符號:

Table 1 Symbols

1.2 分支數

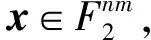
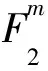
M的線性分支數定義為

分支數反映了密碼方案的擴散性，此外也與差分分析和線性分析相關.分支數達到最大的矩陣稱為MDS矩陣，分支數達到次優的矩陣稱為Near-MDS矩陣.基于分支數，密碼方案的設計者和分析者可以估計活躍S盒的下界，從而評估算法抵抗差分分析和線性分析的能力.

1.3 uBlock算法描述

uBlock算法的整體結構采用PX(Pshufb-Xor)結構(SP結構的一種細化結構)，Pshufb和Xor分別是向量置換和異或運算指令.算法設計采用S盒和分支數的理念，對差分分析和線性分析具有可證明的安全性，同時對于不可能差分分析、積分分析、中間相遇攻擊等分析方法具有相對成熟的分析評估理論支持.此外，uBlock算法適應各種軟硬件平臺，充分考慮了微處理器的計算資源,可以利用SSE,AVX2和NEON等指令集高效實現；硬件實現簡單而有效,既可以高速實現，滿足高性能環境的應用需求,也可以輕量化實現,滿足資源受限環境的安全需求.

uBlock是一族分組密碼算法，分組長度和密鑰長度支持128 b和256 b，分別記為uBlock128/128,uBlock128/256和uBlock256/256，迭代輪數分別為16,24和24.加密算法由輪迭代變換組成，輪變換如圖1所示:

圖1中，基本模塊為：

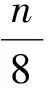
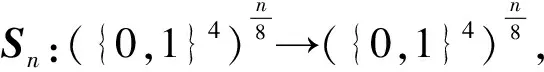
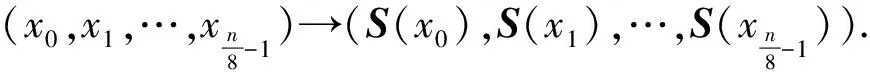
4 b的S盒如表2所示：

Table 2 The 4 bit S Box of uBlock Algorithm

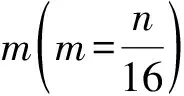
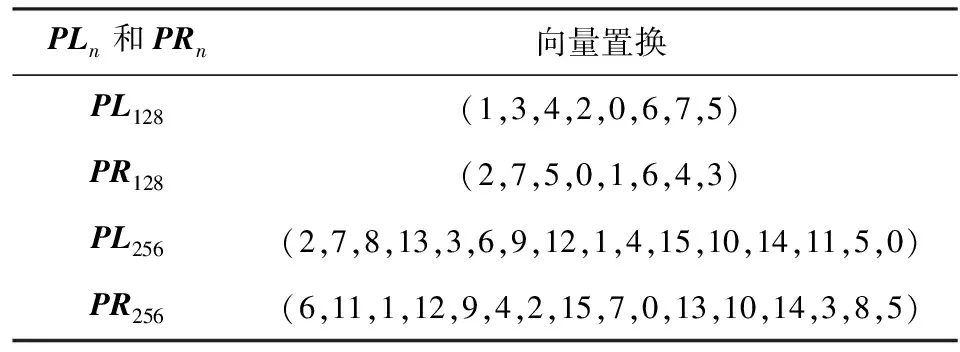
Table 3 PLn and PRn

比如PL128表示為

PL128:({0,1}8)8→({0,1}8)8

(y0,y1,…,y7)→(z0,z1,…,z7)

z0=y1,z1=y3,z2=y4,z3=y6,

z4=y0,z5=y2,z6=y7,z7=y5.

2 uBlock類結構

uBlock算法采用的整體結構是PX結構，其擴散層由2部分組成：一部分是線性變換，即由Feistel結構構造的二元最優擴散層；另一部分是向量置換.在本節中，我們探索一類PX結構的擴散特性，即線性變換部分選取與uBlock算法相同的二元擴散層，向量置換部分與uBlock算法不同的結構，稱之為uBlock類結構，形式如圖2所示：

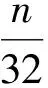
此外，我們觀察到M16用矩陣形式表示出來，恰好為如下形式的分塊矩陣：

其中,

A=Circ(0,0,1,1,1,0,1,1),

B=Circ(1,1,0,1,0,1,1,1),

C=Circ(1,0,1,1,0,0,1,1).

由于

因此

其中Am,Bm,Cm指對角線元素分別為A,B,C，而其余元素為零矩陣的m×m分塊矩陣，即有

我們的目標是探索uBlock類結構的擴散性，并尋找最優的向量置換使得整體結構的擴散性和安全性達到最優，即我們需要考慮的指標有3個：

1)全擴散輪數.全擴散輪數越小，算法的擴散性越強，且可以根據全擴散輪數大致估計算法抵抗不可能差分、積分分析等結構性分析方法的能力.因此，我們旨在尋找可以達到最小全擴散輪數的置換.

2)實現性能.盡可能減少軟件實現中的指令數.

3)4輪超級S盒下的分支數.我們可以根據分支數的概念給出算法活躍S盒的下界，并基于此估計其抵抗差分和線性分析的能力.因此，我們希望分支數越大越好.

2.1 全擴散輪數

擴散最初是由香農在文獻[15]中定義的，意思是一個子塊的輸入影響全部子塊的輸出.文獻[16]證明了抵抗飽和攻擊和不可能差分攻擊的輪數與稱之為全擴散輪數的概念相關,用DR表示全擴散輪數.同時，證明了給定的結構需要至少2DR+1輪來抵抗上述攻擊.因此，在設計分組密碼時,全擴散輪數是一個重要的參考指標.接下來,我們研究uBlock類結構全擴散輪數的下界,首先給出M16的擴散性質：

性質1.輸入向量的漢明重量為1時,經過M16均可擴散到11個位置.

性質2.輸入向量的漢明重量為2時，有如下8種情形在經過M16后可全擴散：

(1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0),

(0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1),

(0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0),

(0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0),

(0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0),

(0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0),

(0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0),

(0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0).

性質3.輸入向量的漢明重量為3時,有400種輸入在經過M16后可全擴散,剩余160種輸入均可擴散到15個位置.

性質4.輸入向量的漢明重量為4時,有1 740種輸入在經過M16后可全擴散,剩余80種輸入均可擴散到15個位置.

性質5.輸入向量的漢明重量為5時,有4 352種輸入在經過M16后可全擴散,剩余16種輸入均可擴散到15個位置.

性質6.輸入向量的漢明重量大于5時,經過M16后均可全擴散.

根據上述6個性質可知,要使經過M16后全擴散,輸入向量的漢明重量至少為2.則對于uBlock類結構,假定輸入向量的漢明重量為1,則經過1輪輪函數后可擴散到11個位置,這11個位置經過2輪至多可擴散到16×5+11=91個位置,經過3輪至多可擴散到45×16+11=731個位置.因此,我們可以給出一系列uBlock類結構的全擴散輪數下界,如表4所示.表4顯示了uBlock類結構具有極強的擴散性.

Table 4 Lower Bound of Full Diffusion Round for uBlock-like Structures

2.2 超級S盒

為了進一步估計算法抵抗差分和線性分析的能力，我們引入超級S盒的概念.uBlock類結構連續4輪輪函數作用在中間狀態X上可以表示為

P°T2°M°T1°S°P°T2°M°T1°S°P°T2°

M°T1°S°P°T2°M°T1°S(X).

(1)

注意到S和T1,T2,P可以交換位置，因此式(1)等價于

P°T2°S°M°S°T1°P°T2°M°T1°P°T2°

S°M°S°T1°P°T2°M°T1(X),

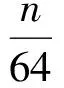
相應的Msuper=T1°P°T2°M°T1°P°T2為超級線性層.因此，可以通過Msuper的分支數來估計算法的活躍S盒數，進而估計其抵抗差分和線性分析的能力，即

Msuper=T1·P·T2·M·T1·P·T2=

(2)

因此，我們可以直接通過式(2)來計算Msuper的分支數.

2.3 等價類劃分準則

為了減少搜索空間，我們進一步探索uBlock類結構的等價類劃分準則，并給出最優向量置換的搜索策略.首先，uBlock類結構可用圖3描述：

顯然，圖4(a)和4(b)兩種形式是等價的，此時假若MQ=QM，則圖4(c)與圖4(a)和4(b)也是等價的，即可得到圖4(d)與4(a)等價，即假若MQ=QM，則P與QPQ-1在uBlock類結構中具有相同的密碼學性質.

于是，我們可以給出如下搜索策略：

策略1.uBlock類結構最優向量置換的搜索策略.

步驟1.確定使得MQ=QM的所有置換Q；

步驟2.對得到的所有置換Q，則P與QPQ-1屬于同一個等價類.

步驟3.對每一個等價類中的代表元，測試算法整體的全擴散輪數.

步驟4.對全擴散輪數最小的置換，檢測Msuper及其逆變換的分支數.

3 應 用

我們將第2節的搜索策略應用于128 b分組和256 b分組的uBlock類結構中，尋找最優向量置換.對于128 b和256 b分組的uBlock類結構，我們選擇與uBlock算法中的結構相同，即P層是PL和PR的并置，且均為面向字節的向量置換，因此我們可以進一步優化搜索策略1.

3.1 128 b分組

128 b分組的uBlock類結構的擴散層描述如圖5所示:

其中

則

其中，I為單位矩陣，O為零矩陣.

由表3可知，128 b分組的uBlock類結構至少需要2輪全擴散.因此，我們僅需要尋找2輪全擴散下的最優向量置換.出于性能的考慮，若PL或PR是恒等變換，則輪函數少一個指令，此時算法軟件性能會有所提升.使用等價類劃分技術，我們發現PL和PR是恒等變換時均有27個等價類滿足2輪全擴散.部分具體實例在附錄中給出.

此外，我們考慮4輪超級S盒下，擴散層的分支數達到最優的情形.由于

我們可將擴散層看作一個2×2的分塊矩陣，考慮其為MDS矩陣，即分支數為3.此時，根據超級S盒和分支數的概念，可知其4輪至少有24個活躍S盒(與uBlock-128中選擇的向量置換在4輪時的活躍S盒數一致).

Q1A2=A2Q1,Q2C2=C2Q2,

Q1B2=B2Q2,Q2B2=B2Q1.

策略2.uBlock-128最優向量置換的搜索策略.

步驟1.尋找使得Q3·A2=A2·Q3的所有置換Q3，記為集合SQ3；

步驟2.尋找使得Q4·C2=C2·Q4的所有置換Q4，記為集合SQ4；

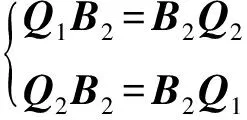
步驟4.使用集合對SQ1,Q2中的置換，對P的全空間做等價類劃分，若

則

步驟5.對每一個等價類中的代表元，輸出4輪超級S盒下擴散層的分支數為3的置換P.

此時，當PL,PR其中一個為恒等置換時，不存在MDS矩陣.所以我們進一步將PL,PR其中一個放寬為循環移位，此時，滿足2輪全擴散且超級擴散層為MDS時的等價類共有3 556個.部分具體實例在附錄中給出.這一結果顯示uBlock-128算法選擇的向量置換是最優的，不存在可進一步減少指令數的最優向量置換對.受益于我們的等價類劃分方法，最優向量置換對的數量大幅減少，這對后續進一步篩選滿足其他安全性指標時提供了便利.

3.2 256 b分組

256 b分組的uBlock類結構的擴散層描述如圖6所示.其中，

T1=(1,5,2,6,3,7,4,8),

T2=(1,3,5,7,2,4,6,8)，

我們首先關注256 b分組的uBlock類結構的全擴散輪數，得到定理1.

定理1.對于256 b分組的uBlock類結構，PL,PR選擇基于字節的向量置換時，其全擴散輪數的下界為3.

證明.將256 b分組的uBlock類結構看作是8個分支的輸入，從左到右依次是第1到第8個分支，每個分支都為8 b.我們假定輸入向量漢明重量為1，為(0,1,0,…,0)，則經過一輪輪函數的輸出為：

第1個分支為(a1,a2,a3,a4)，其中

a1=(0,0),a3=(0,1),a2=a4=(1,1).

第5個分支為(b1,b2,b3,b4)，其中

b1=b2=(1,1),b3=b4=(1,0).

其余分支的漢明重量均為零.注意到，(a1,a2,a3,a4)中的元素只能置換到下一輪M16輸入的左半支，(b1,b2,b3,b4)中的元素只能置換到右半支.然而，要使2輪全擴散，進入下一輪4個M16的向量漢明重量只能為(2,2,3,4)和(2,3,3,3)，且漢明重量為2的部分只能有4種搭配，即(a1,b1),(a1,b2),(a3,b3)和(a3,b4).然而由第2節可知，對于M16，輸入向量漢明重量為2時，只有8種情形可以全擴散，這8種情形左右半支漢明重量均為1，且非零位置只有(1,0)與(1,0)搭配和(0,1)與(0,1)搭配.因此，256 b分組的uBlock類結構至少需要3輪全擴散.

由表3可知，若256 b分組的uBlock類結構的P層使用更加細粒度的置換，則可能會在2輪達到全擴散.考慮到在算法實現時大置換實現效率不佳，因此我們并未嘗試尋找大置換下2輪達到全擴散的情形.

接下來，我們試圖尋找3輪全擴散下256 b分組的uBlock類結構的最優向量置換.對于PL和PR，我們與uBlock-256一樣，考慮面向字節的向量置換.考慮到軟件性能的提升，我們假定PL或PR其中一個為恒等變換，此時我們找到大量滿足3輪全擴散的置換，在附錄中我們給出了部分實例.

此外，我們考慮4輪超級S盒下，擴散層的分支數為4的情形.由于

我們可將擴散層看作一個4×4的分塊矩陣，考慮其分支數為4的情形.此時，根據超級S盒和分支數的概念，可知其4輪至少有32個活躍S盒(與uBlock-256算法中的置換在4輪時的活躍S盒一致).

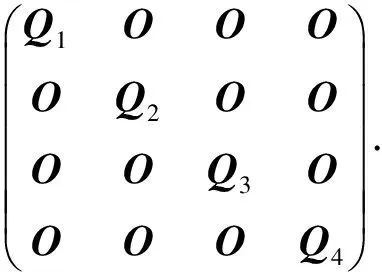
Q1A2=A2Q1,Q2A2=A2Q2,

Q3C2=C2Q3,Q4C2=C2Q4,

Q1B2=B2Q3,Q2B2=B2Q4,

Q3B2=B2Q1,Q4B2=B2Q2.

因此，我們給出如下搜索策略3:

策略3.uBlock-256最優向量置換的搜索策略.

步驟1.尋找使得Q3·A2=A2·Q3的所有置換Q3，記為集合SQ3；尋找使得Q4·C2=C2·Q4的所有置換Q4，記為集合SQ4.

步驟2.尋找集合對SQa,Qb，使得Qa∈SQ3,Qb∈SQ4滿足Qa·B2=B2·Qb；尋找集合對SQc,Qd，使得Qc∈SQ3,Qd∈SQ4滿足Qd·B2=B2·Qc.

步驟3.取(Q1,Q2)∈SQa,Qb,(Q3,Q4)∈SQc,Qd,對P的全空間做等價類劃分，即若

步驟4.對每一個等價類中的代表元，輸出3輪全擴散且4輪超級S盒下擴散層的分支數為4的置換P.

經過實驗，當PL和PR其中一個為恒等變換時，我們并未找到3輪全擴散且在4輪超級擴散層分支數為4的置換對.對于PL和PR均為一般置換時，存在大量3輪全擴散且在4輪超級擴散層分支數為4的置換對，部分具體實例在附錄中給出.

在僅考慮全擴散輪數、性能和超級擴散層的分支數這3個指標時，我們的結果與uBlock-256使用的向量置換是一致的.然而，本文中給出的等價類劃分規則可以將滿足條件的置換對縮小到較小的范圍，這將為后續進一步測評其抵抗其他分析方法時提供便利.

4 總 結

在本文中，我們探索uBlock類結構最優向量置換的選取.對于uBlock算法族，擴散層分為2部分：一部分是由Feistel結構構造的16維最優二元擴散層，另一部分為2個向量置換的并置.我們的目標是在二元擴散層固定的前提下，尋找最優向量置換來提升算法整體的安全性和實現效率.本文中，我們主要的評價指標為算法的全擴散輪數、軟件性能和4輪超級S盒下擴散層的分支數.

首先，我們探索uBlock類結構的擴散性，給出了不同規模下uBlock類結構全擴散輪數的下界.其次，為了減少搜索復雜度，基于uBlock類結構的特點，我們提出了等價類劃分技術.進一步，基于全擴散輪數最優、軟件性能優良和超級擴散層的分支數，我們設計了uBlock類結構最優向量置換的搜索策略.最后，將搜索策略應用于128 b和256 b分組的uBlock類結構中.在具體應用時，結合不同分組長度下算法的特點，我們進一步優化了最優向量置換的搜索策略，并給出具體實例.

對于128 b分組的uBlock類結構，若PL和PR其中一個為恒等變換時，存在滿足2輪全擴散的置換對；然而，不存在2輪全擴散且超級擴散層分支數最優的置換對.因此，我們將PL或PR放寬到循環移位后，給出了全擴散輪數及超級擴散層分支數均最優的置換對.對于256 b分組的uBlock類結構，我們證明了其最優全擴散輪數為3輪，若PL或PR其中一個為恒等變換時，存在3輪全擴散的置換對，然而不存在全擴散輪數為3且超級擴散層的分支數為4的置換對.與uBlock算法相比，在僅考慮全擴散輪數這一指標時，算法所需的向量置換指令更少，從而有更高的軟件實現效率.在考慮全擴散輪數和超級擴散層分支數2個指標后，我們的結果與uBlock算法中使用的向量置換是一致的，表明uBlock算法選擇的向量置換是最優的，不存在可進一步減少指令數的向量置換對，但是我們提出的等價類劃分規則可以將置換對的數量大幅減少，為后續uBlock類算法的設計提供技術支持.

作者貢獻申明：李曉丹提出了算法思路，撰寫論文；吳文玲提出指導意見并修改論文；張麗提出修改意見.