鉸接式柔性鉆桿的參數化設計
薛世華,羅敏,王晶,林志強
(1.東北石油大學機械科學與工程學院,黑龍江大慶 163318;2.東北石油大學數學與統計學院,黑龍江大慶 163318)
0 前言
柔性鉆具是超短半徑水平井鉆井中的主要工具,其結構的合理性直接影響超短半徑水平井鉆進的成功率。近年來,國內學者[1-5]大多采用力學分析和數值模擬相結合的方法對柔性鉆具進行結構設計與強度評價。楊決算和鄭瑞強[6]通過對茂加65-82雙分支超短半徑水平井的井身結構以及分支井眼軌道的設計,提高了原井的產油量。張紹林等[7]基于十字萬向節結構,通過理論分析,設計出了單節彎曲角度為5°的柔性鉆具。帥健和劉春[8-9]通過理論分析,編制了計算程序來模擬計算鉸接式鉆具組合的靜態特性和動態響應。陳長青等[10]通過穿越專用柔性鉆桿的結構設計及工藝研究,得到了對鉆桿質量和疲勞壽命影響最大的兩個指標。而國外學者多數通過理論分析對含鉸接的柔性結構進行研究。FERRI[11]建立了含有套筒式連接鉸的非線性模型,并將零件之間的接觸力等效為零件受壓時的有效非線性單向彈簧。SHI和ATLURI[12]通過對Ramberg-Osgood函數的分析,發現了庫侖摩擦鉸鏈引起的遲滯特性存在于柔性結構中。SHABANA[13]發現絕對節點坐標方法在分析柔性多體動力學中能夠得到大量的應用。NOGUCHI和KANADA[14]在不同約束條件下,通過對并聯機構中的球鉸鏈進行剛度分析,得出了鉸鏈間的鉸接度數會對鉸鏈剛度產生一定影響;LOBONTIU和GARCIA[15]將柔性鉸鏈建模為復雜的彈簧,通過彈簧的彈性響應就能夠測得柔性鉸鏈的軸向、彎曲和剪切載荷。綜上所述,國內外學者對于柔性結構的參數化設計研究相對較少,因此作者采用理論分析與數值模擬相結合的方法,開展了鉸接式柔性鉆桿參數化設計的研究。
1 柔性鉆桿結構設計方法
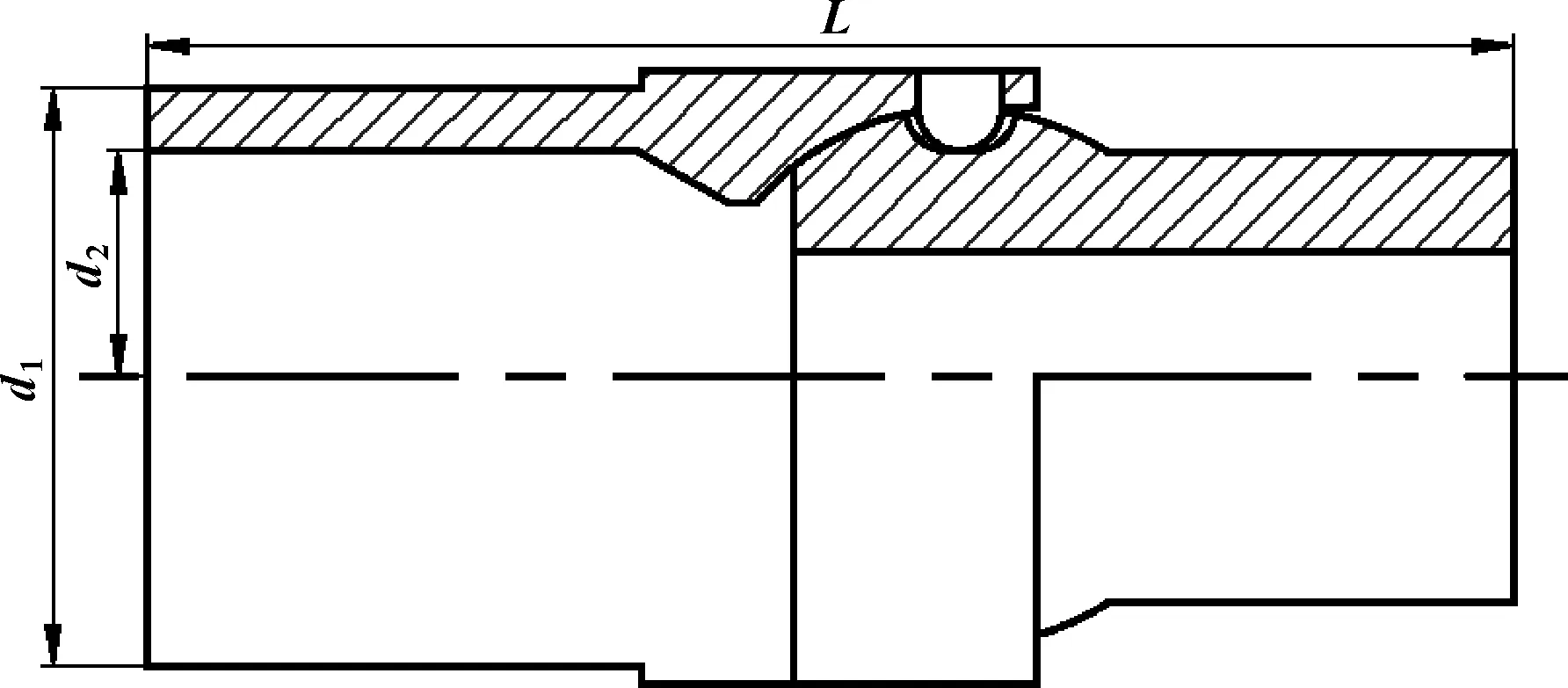
超短半徑水平井柔性鉆具主要由5個部分組成:鉆具上三連接、導向篩管、柔性鉆桿、鉆具下三連接和鉆頭,柔性鉆具組合結構如圖1所示。柔性鉆桿通過多個柔性短節鉸接在一起,在外部導向篩管的帶動下能夠較為靈活地產生側向彎曲。其中柔性鉆桿由上球座、軸承外套、滾動軸承、球座護帽、球頭柱鍵、球頭連桿和O形密封圈構成,其結構如圖2所示。
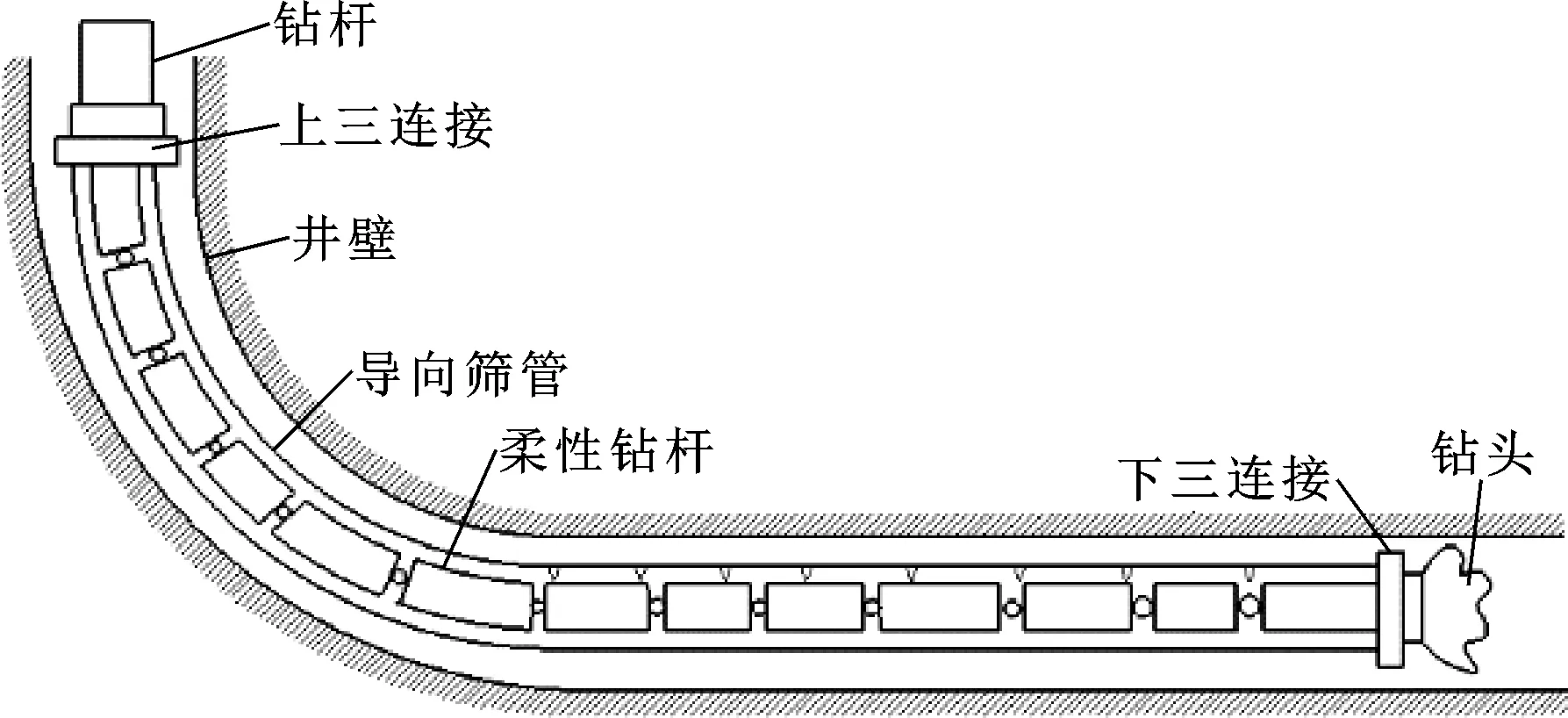
圖1 柔性鉆具組合結構
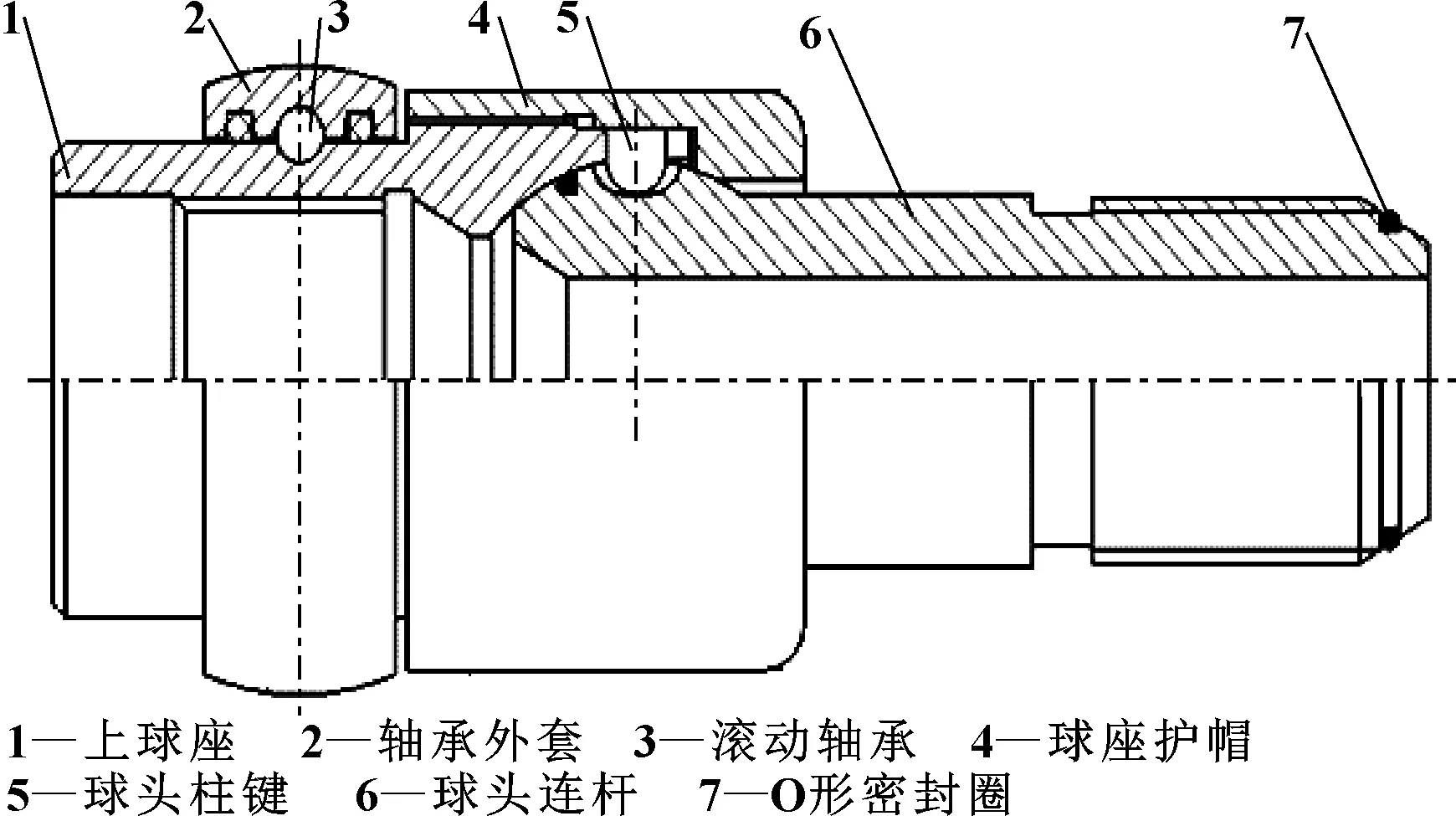
圖2 柔性鉆桿的結構
1.1 柔性鉆桿結構設計流程
為了使柔性鉆桿能通過曲率半徑較小的井眼,使其在滿足強度的條件下彎曲度最大,在保持球頭柱鍵直徑不變的情況下,對影響柔性鉆桿彎曲度的5個主要參數進行了設計計算。5個主要參數分別為柔性鉆桿的最大外徑d、上球座的外徑d1、柔性鉆桿的單節長度L、單節彎曲角度β、凹槽長度l。首先根據柔性鉆桿扭轉時的強度條件,求出上球座的外徑d1,進而求出柔性鉆桿的最大外徑d;然后根據造斜段柔性鉆桿與導向篩管的幾何關系,求出柔性鉆桿的單節極限長度L;再根據造斜段和水平段柔性鉆桿和導向篩管的接觸狀態,求出鉸接度數的最小值和最大值,確定鉸接度數的取值范圍;最后根據鉸接度數的取值范圍,確定鉸接處的彎曲角度,進而求出凹槽的長度。柔性鉆桿的結構設計流程如圖3所示。
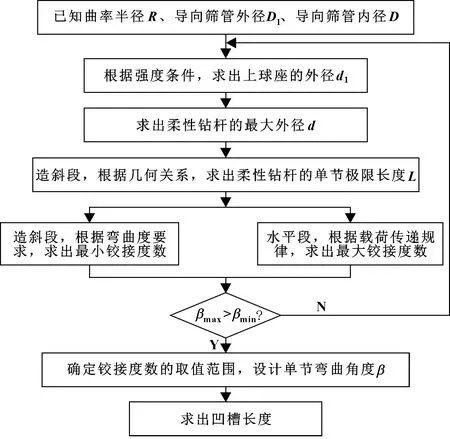
圖3 柔性鉆桿結構設計流程
1.2 柔性鉆桿最大外徑的設計
在水平段鉆進時,為了使柔性鉆桿能夠順利地通過導向篩管,不至于由于過度接觸而被卡死,可以通過增大柔性鉆桿與導向篩管內壁之間的環空間隙來增大柔性鉆桿的彎曲度。保持導向篩管的內徑不變,減小柔性鉆桿的最大外徑,可以增大環空間隙。由于柔性鉆桿的最大外徑位于上球座的軸承外套處,所以可以通過減小上球座的外徑來減小柔性鉆桿的最大外徑。根據圓軸的扭轉強度條件:
(1)
(2)
可得上球座的外徑d1為
(3)
式中:M為柔性鉆桿上的扭矩;d2為上球座的內徑;τs為材料的扭轉屈服應力。由式(3)可以確定柔性鉆桿的最大外徑。
1.3 柔性鉆桿單節長度的設計
為了確定單節柔性鉆桿的長度,在造斜段時,假設導向篩管為剛性彎曲外殼,柔性鉆桿也為剛性,在承受鉆壓和扭矩的作用下不發生變形。造斜段,柔性鉆桿與導向篩管的幾何關系如圖4所示。
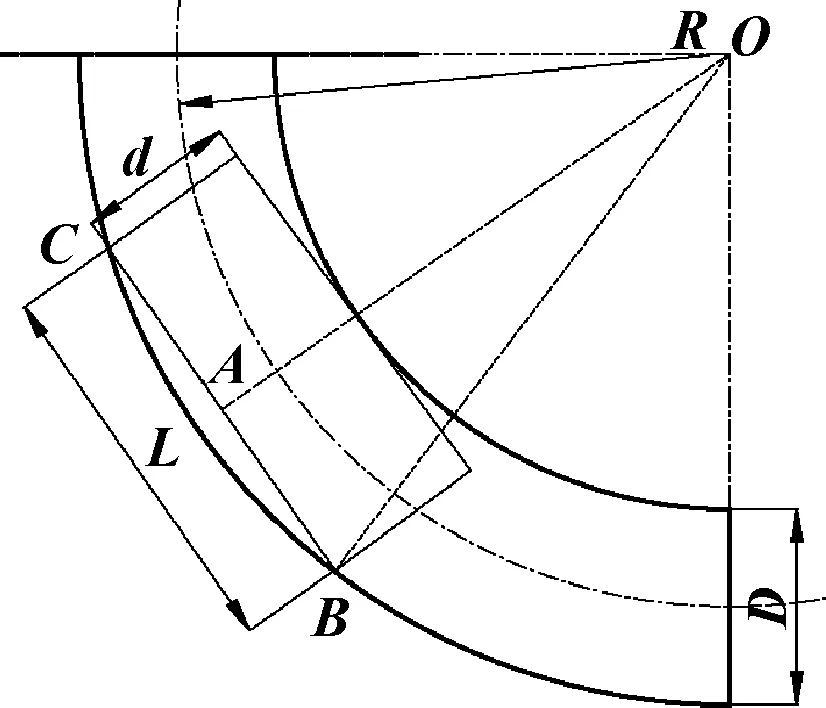
圖4 造斜段柔性鉆桿和導向篩管的幾何關系
在直角三角形OAB中,各個尺寸之間的幾何關系為
(R+D/2)2=(L/2)2+(R-D/2+d)2
(4)
式中:R為曲率半徑;D為導向篩管內徑;d為柔性鉆桿的最大外徑;L為柔性鉆桿的單節長度。
所以,單節柔性鉆桿的極限長度為
(5)
1.4 計算彎曲角度的范圍
假設柔性鉆桿與導向篩管都為剛性的條件下,由圖4可以看出,在造斜段,當一定長度的柔性鉆桿通過曲率半徑為R的導向篩管時,單節柔性鉆桿的彎曲角度
(6)
鉆具在水平段作業時,柔性鉆桿除了承受自身重力外,還要承受軸向力并且傳遞扭矩。由于柔性鉆桿會因自重下垂,當柔性鉆桿的鉸接結構轉過的角度較小時,不會與導向篩管內壁發生接觸;當柔性鉆桿的鉸接結構轉過的角度使其與導向篩管內壁剛好接觸時,柔性鉆桿與導向篩管內壁為摩擦接觸,這時會損失掉一部分扭矩;當柔性鉆桿的鉸接結構轉過角度較大時,柔性鉆桿與導向篩管內壁接觸并被卡死,使鉆壓損失過大,不能繼續鉆進。由此可見,第一種情況是最理想的狀態。所以柔性鉆桿的單節彎曲角度除大于滿足通過彎管條件的轉角外,還應小于直管內兩節柔性鉆桿之間的最大轉角。水平段柔性鉆桿與導向篩管的幾何關系如圖5所示。
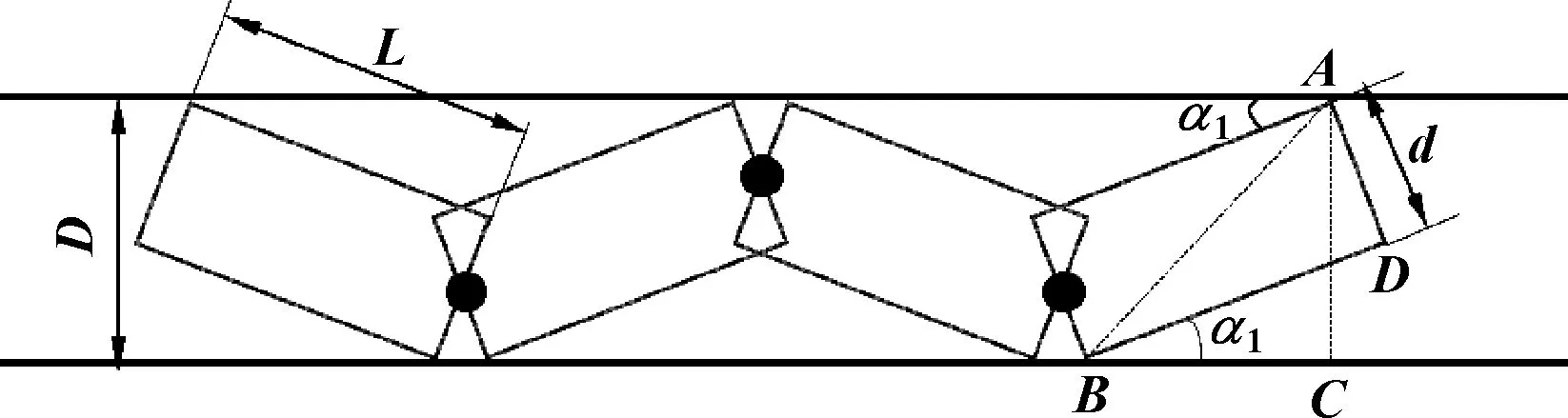
圖5 水平段柔性鉆桿與導向篩管的幾何關系
由圖中的直角△ABC和直角△ABD可知
所以單節柔性鉆桿的彎曲角度β<2α1,即
(7)
式中:D為導向篩管的內徑;d為柔性鉆桿的最大外徑;L為柔性鉆桿的單節長度。
1.5 凹槽長度的設計
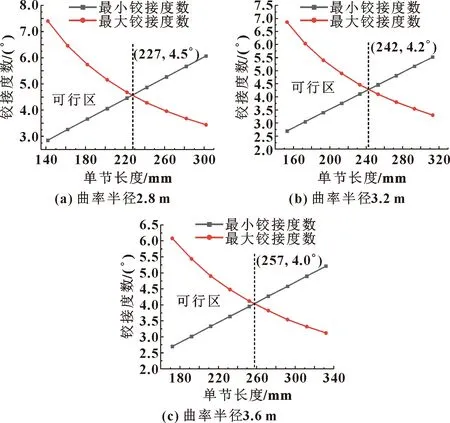
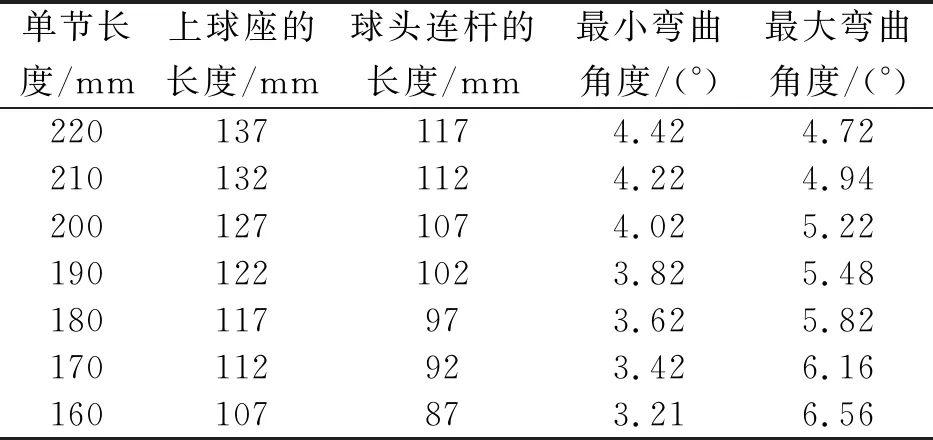
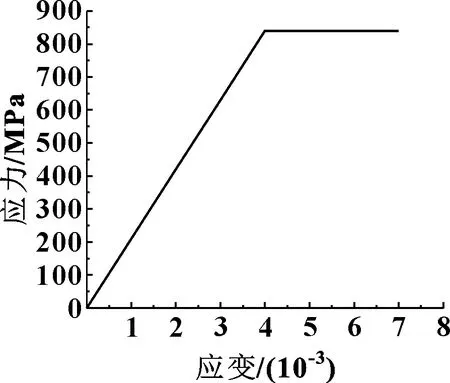
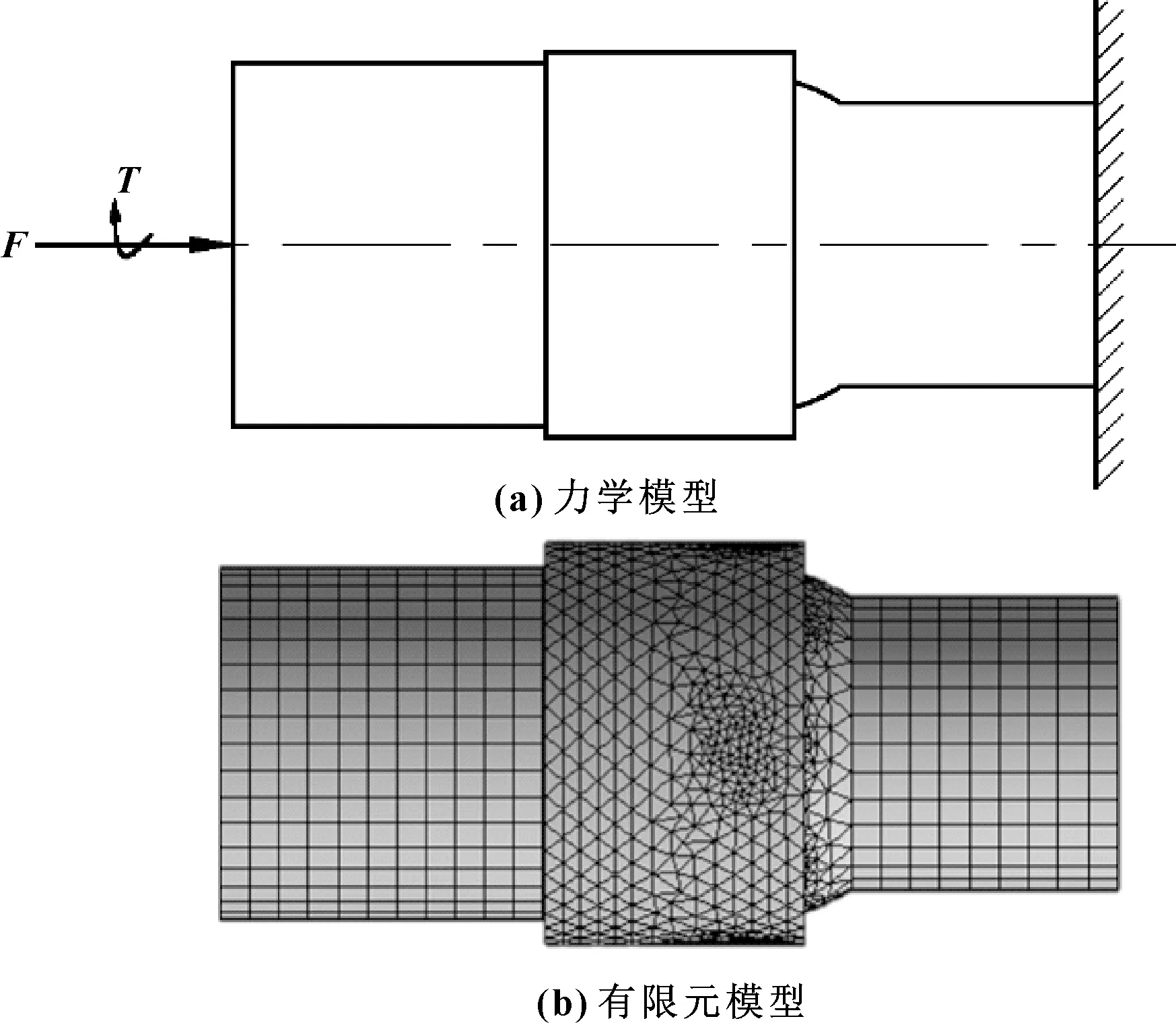
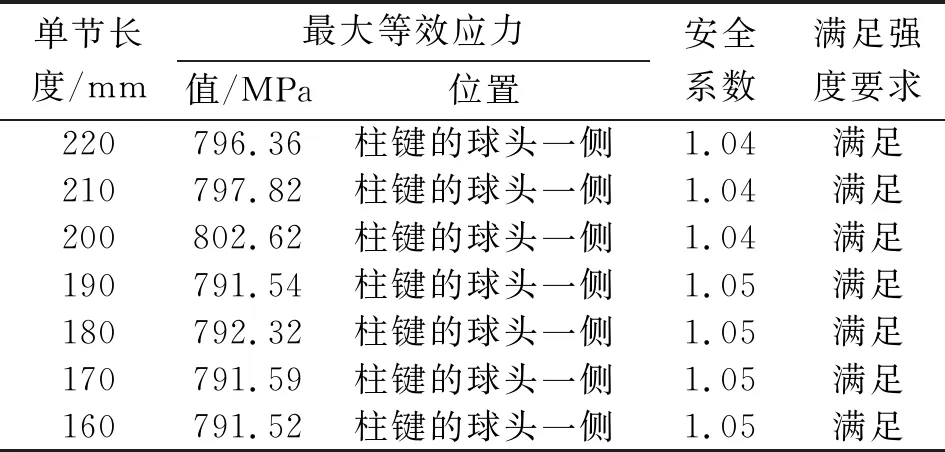
柔性鉆桿中球頭柱鍵與凹槽的配合構成一個可控鉸接結構,使柔性鉆桿能夠在一定的方向上旋轉一定的角度,從而實現造斜鉆進。由于凹槽位于球頭連桿上,根據上球座與球頭連桿的配合關系以及球頭連桿的結構特點可知,凹槽的長度l的取值范圍為d3 圖6 柱鍵與凹槽結構 由圖中的幾何關系可知 (8) 所以凹槽的長度為 (9) 式中:β為柔性鉆桿的單節彎曲角度;d3為柱鍵的直徑;r1為球頭連桿球頭處的半徑。 在柔性鉆桿中,球頭連桿和上球座之間通過接觸來傳遞軸向力,球頭柱鍵與球頭連桿凹槽通過接觸傳遞扭矩。所以對柔性鉆桿結構進行分析計算時,忽略結構中一些非主要影響因素的零件,將柔性鉆桿簡化為由上球座、球頭連桿和球頭柱鍵組成的簡單裝配體,如圖7所示。其計算實例的主要結構參數:柔性鉆桿所受的扭矩M=2 kN·m,材料為35CrMo,屈服極限σs=835 MPa,τs=0.6σs=501 MPa,導向篩管的內徑D=95 mm,上球座的內徑d2=54 mm,球頭連桿上的球頭半徑r1=32 mm,柱鍵直徑d3=10 mm,曲率半徑R=2.8~3.6 m。 圖7 簡化后的單節柔性鉆桿 根據式(3)可得,在滿足強度的條件下,上球座的外徑d1>55 mm。所以根據柔性鉆桿的結構特點,將上球座的外徑設計為d1=64 mm,柔性鉆桿的最大外徑d=86 mm。 根據式(5)計算出曲率半徑分別為2.8、3.2、3.6 m時,單節柔性鉆桿的極限長度分別為452、483、512 mm。 根據式(6)和式(7)可以求出不同的曲率半徑以及不同的單節長度所對應的鉸接度數的取值范圍,如圖8所示。 圖8 柔性鉆桿不同單節長度對應的鉸接度數范圍 由圖8可以看出:虛線左側區域滿足最小鉸接度數小于最大鉸接度數,為可行區域。在可行域內,單節長度越短,鉸接度數的取值范圍就越大,能取到的最大鉸接度數就越大;曲率半徑越大,單節柔性鉆桿極限長度越大,在滿足鉸接度數取值范圍的條件下,3種曲率半徑對應的單節柔性鉆桿的極限長度分別為227、242、257 mm。能夠同時滿足3種曲率半徑的單節柔性鉆桿的極限長度為227 mm。 以曲率半徑2.8 m為例,由圖8可以得到柔性鉆桿的不同單節長度對應的彎曲角度的取值范圍,如表1所示。 表1 曲率半徑2.8 m時彎曲角度的取值范圍 根據表1中柔性鉆桿的不同單節長度對應的彎曲角度的取值范圍,當彎曲角度取4.5°時,可以滿足所有不同單節長度的柔性鉆桿,所以將單節柔性鉆桿的彎曲角度設計為4.5°。 根據前面第1.5節的分析可知,凹槽的長度與單節柔性鉆桿的彎曲角度有關,所以當彎曲角度設計為4.5°時,根據式(9)可以計算出球頭連桿上凹槽的長度為14.9 mm,并且滿足凹槽長度的取值范圍。 柔性鉆桿的材料為35CrMo,屈服極限為835 MPa,強度極限為980 MPa,彈性模量為210 GPa,泊松比0.3,摩擦因數為0.2。假設材料為理想彈塑性,其應力應變關系曲線如圖9所示。 圖9 應力應變關系曲線 球頭柱鍵與凹槽以及球頭與球碗之間的接觸為摩擦接觸,采用增廣拉格朗日法計算接觸應力,其計算原理如式(10)所示: FNormal=kNormalxp+λ (10) 其中:FNormal為接觸力;kNormal為接觸剛度;xp為穿透量;λ為拉格朗日項。 其邊界條件為:右端全固定,左端施加40 kN的軸向力和2 kN·m扭矩。網格劃分:上球座和球頭連桿的圓柱部分采用六面體網格劃分,球頭和球碗部分采用四面體網格劃分,柱鍵和凹槽處的網格加密,單元尺寸為1 mm,網格質量為0.81。柔性鉆桿的力學模型與有限元模型如圖10所示。 圖10 柔性鉆桿的力學模型與有限元模型 通過以上分析,當單節柔性鉆桿的彎曲角度為4.5°、凹槽長度為14.9 mm時,柔性鉆桿能通過3種不同的曲率半徑,并且能滿足5種不同的單節長度所對應的鉸接度數的取值范圍。對柔性鉆桿這5種不同的結構參數進行了數值模擬,數值模擬的結果如表2所示。 表2 不同結構參數的數值模擬 由表2可以發現:柔性鉆桿的單節長度與最大等效應力之間為非線性關系。隨著單節長度的增加,最大等效應力相對穩定,應力值之間差值最大不超過6 MPa,并且都滿足強度要求。又考慮到加工量的問題,在彎曲角度的取值范圍內,選擇最大的單節長度作為設計尺寸,所以將柔性鉆桿的單節長度設計為220 mm。柔性鉆桿各個參數的設計值如表3所示。 表3 單節柔性鉆桿的設計尺寸 (1)根據柔性鉆桿的幾何關系、強度條件、彎曲度要求,推導出了單節柔性鉆桿最大外徑、單節長度、彎曲角度的取值范圍以及凹槽長度的計算公式。該公式揭示了各參數之間的相互關系,為柔性鉆具的設計提供了理論基礎。 (2)為同時滿足不同的井眼曲率半徑,設計并確定了曲率半徑為2.8 m時,柔性鉆桿的關鍵尺寸:上球座的外徑為64 mm,柔性鉆桿的最大外徑為86 mm,單節長度為220 mm,彎曲角度為4.5°,凹槽長度為14.9 mm。 (3)考慮到球頭柱鍵與凹槽之間以及球頭與球碗之間的接觸非線性,采用有限單元法建立了柔性鉆桿的有限元模型。對不同結構參數的柔性鉆桿進行仿真分析,可得各結構均滿足強度要求。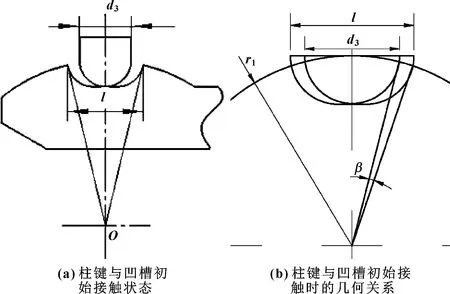
2 結構設計的計算實例
2.1 柔性鉆桿最大外徑的確定
2.2 單節柔性鉆桿的極限長度的確定
2.3 單節柔性鉆桿彎曲角度的確定
2.4 凹槽長度的確定
3 柔性鉆桿的仿真分析
3.1 力學模型的建立
3.2 不同結構參數的數值模擬

4 結論

