一種三自由度弱耦合并聯機構運動學分析

謝俊，左飛飛，楊啟志，李玉萍

(1.江蘇大學機械工程學院，江蘇鎮江 212013；2.江蘇大學農業裝備工程學院，江蘇鎮江 212013)

0 前言

兩平移一轉動(Two Translation and One Rotation, 2T1R)并聯機構兼顧移動和轉動輸出特性，在生產實踐中應用廣泛。毛軍華、薛城等人[1-2]研究了2T1R型并聯康復機器人；王成軍、謝俊、汪志煥等[3-5]將2T1R并聯機構應用于物料篩分領域。在機構學研究方面，黃秀琴等[6]對2T1R新構型并聯機構進行位置分析；劉延斌、董倩文等[7-8]針對一種3-RPR并聯機構分析其運動學特性；鄧嘉鳴等[9]研究了(RPa‖3R)-R+RSS型無寄生運動并聯機構。在機構耦合研究方面，馬履中等[10]研究了三平移弱耦合并聯機器人；范彩霞等[11]對完全解耦型2R并聯機構進行了運動學分析；TIAN、沈惠平[12-13]等研究了3T1R機構的耦合度和解耦特性。

上述并聯機構主要存在兩個問題：(1)未兼顧機構耦合度與解耦分析，使得所設計的并聯機構不能同時實現運動學分析的簡化與控制方式的解耦，不利于機構的快速設計與應用；(2)解耦分析未涉及控制方式耦合程度的判別，輸入-輸出控制方式的解耦特性不明確。

基于方位特征集理論，本文作者提出一種2T1R并聯機構。該并聯機構耦合度為1，位置分析所需聯立的運動支鏈數較少；基于位置分析求解動平臺工作空間和Jacobian矩陣，在并聯機構約束動平臺輸出三自由度運動的前提下，3種輸入-輸出控制方式解耦。此外，文中還對該機構速度和加速度進行了研究。

1 并聯機構設計及拓撲分析

1.1 機構設計

根據基于方位特征集(Position and Orientation Characteristic, POC)的并聯機構拓撲結構設計理論[14]，文中提出的2T1R并聯機構由動平臺1、靜平臺0和單開鏈(Single Opened Chain, SOC)Ⅰ、Ⅱ、Ⅲ組成，并聯機構的拓撲結構為PRR+2-PRRU。

如圖1所示，單開鏈Ⅰ(P1‖R1‖R2-U1)的結構等價于(P1‖R1‖R2‖R11⊥R12)，單開鏈Ⅱ(P2‖R3‖R4-U2)的結構等價于(P2‖R3‖R4‖R21⊥R22)，單開鏈Ⅲ結構為(P3‖R5‖R6)。靜平臺0上各移動副軸線布置關系為：移動副P1、P2、P3分別沿x軸、z軸、y軸方向布置，此外，移動副P1、P2、P3軸線兩兩垂直。

圖1 2T1R并聯機構結構簡圖

1.2 機構自由度計算

并聯機構的POC方程[14]分別為

(1)

(2)

式中：Msj為支鏈中第j個子SOC的POC集,j=1,2,…,k；Mbi為第i條支鏈末端的POC集,i=1,2,…,g；Mpa為機構動平臺的POC集。

(1)機構的拓撲結構

如圖1所示，組成并聯機構的3條單開鏈Ⅰ、Ⅱ、Ⅲ的拓撲結構分別為

SOC1{-P1‖R1‖R2-U1-}

SOC2{-P2‖R3‖R4-U2-}

SOC3{-P3‖R5‖R6-}

靜平臺0上，以單開鏈Ⅲ末端點O′為基點進行分析。

(2)確定各支鏈POC集

由式(1)可知：

并聯機構的全周自由度公式[14]為

(3)

其中：

(4)

(3)確定各支路獨立方程數ξLj

該機構可分解為2個獨立回路，其組成分別為

SOC1{-P1‖R1‖R2-U1-P3‖R5‖R6-}

SOC2{-P2‖R3‖R4-U2-}

它們的獨立位移方程數計算如下：

單開鏈Ⅰ和Ⅲ組成的子并聯機構構成第1個獨立回路，由式(4)可得：

ξL1=dim.{Mb1∪Mb3}=

由式(2)可知該子并聯機構的POC集：

上述子并聯機構與單開鏈SOC2組成第2個獨立回路，由式(4)可得

ξL2=dim.{Mpa(1-3)∪Mb2}=

(4)確定該并聯機構自由度

由式(3)可得該并聯機構自由度為

因此，該并聯機構自由度為3。由驅動副存在準則[14]選取靜平臺0上P1、P2、P3為驅動副。如圖1所示，驅動副P1、P2、P3提供往復直線運動，通過并聯機構約束動平臺輸出2T1R三自由度運動。

1.3 機構耦合度κ分析

由基于單開鏈單元的機構組成原理[14]可知，任意機構可分解為若干個基本運動鏈；而ν個獨立回路的基本運動鏈可進一步分解為ν個單開鏈SOC(Δj) (j=1,2,…,ν),而第j個單開鏈(SOCj)的約束度定義為

(5)

其中:

式中：mj為第j個SOCj的運動副數；Ij為第j個SOCj的驅動副數。

由∑Δj=0可知，基本運動鏈的耦合度κ定義為

(6)

耦合度[14]κ與機構構型的復雜程度有關，它反映各運動回路變量間的依賴程度：

(1)當κ=0時，機構基本運動鏈間完全解耦，其運動學和動力學分析可單獨求解。

(2)當κ>0時，機構基本運動鏈的運動學和動力學分析需聯立多個回路求解。

特別的，當κ=1的多回路機構，可用一維搜索法得到位置分析的全部實數解。

第1.2節已計算出2個回路的獨立位移方程數，分別為ξL1=ξL2=5，且各回路驅動副數目分別為I1=2、I2=1，由式(5)可知約束度Δ1、Δ2分別為

Δ1+Δ2=0→BKC=1

即該機構基本運動鏈數為1。由式(6)可知該機構耦合度κ為1，即該機構位置分析的全部實數解可用一維搜索法得到。

2 位置分析

2.1 坐標系的建立

如圖2所示，靜平臺0與動平臺1均為矩形，二者平行布置，動平臺1位于靜平臺0正上方，且相距為L0；以動平臺1中心P為原點建立動坐標系{P}：P-uvw，且u軸平行于動平臺長度方向，并指向A2，w軸豎直向上垂直于動平臺，v軸由右手定則確定；同理以靜平臺0中心O為原點建立定坐標系{O}：O-xyz。設驅動副P1運動量為X，驅動副P2運動量為Z時，動平臺與x軸夾角為β，連桿A2B2、連桿B2C2與連桿A3B3與x軸的夾角分別為θR4、θR3和θR5。

圖2 2T1R并聯機構運動學模型

該并聯機構的結構參數為：靜平臺0長為2l1，寬為2l2，動平臺1長為2l3，寬為2l4；其他尺寸B3C3=l5，A3B3=l6，A2B2=l7，B2C2=l8，C2D2=l9。

2.2 位置正解分析

機構位置正解[15]即已知該機構的輸入參數(X,Y,Z)，求解動平臺的位姿(x,y,β)。

(1)x、y求解

如圖1所示，該并聯機構運動過程中，移動副P1的移動量即為動平臺沿u軸向的移動量，則有：

x=X

(7)

如圖2所示，在定系{O}中C3=(-l1,Y,0)，B3=(-l1,Y,l5)，在動系{P}中A3=(0,-l4,0)。將點A3變換至定系{O}中：

(8)

(9)

進一步，式(9)整理可得：

(10)

(2)β求解

如圖2所示，由單開鏈Ⅱ與單開鏈Ⅲ在x軸與z軸方向的投影，單開鏈Ⅰ與單開鏈Ⅱ在x軸方向的投影組成的封閉回路[16-18]，可建立如下方程：

l5+l6sinθR5+l3sinβ=L0+Z

(11)

l6cosθR5+l3cosβ+l7cosθR4+l8cosθR3+l9=2l1

(12)

l9+l8cosθR3+l7cosθR4+l3cosβ=l1+X

(13)

將式(13)整理為l8cosθR3+l7cosθR4=l1+X-l9-l3cosβ，并代入式(12)中，整理可得：

(14)

進一步，將式(14)各式平方后相加可得：

(15)

進一步，整理式(15)可得：

Asin2β+Bsinβ+C=0

(16)

其中：

解式(16)可得：

(17)

即有：

β=arcsinU

(18)

2.3 位置反解分析

機構位置反解即已知動平臺位姿(x,y,β)，反求該機構的輸入參數(X,Y,Z)。

(1)X、Y求解

(19)

(2)Z求解

由式(15)可知：

(L0+Z-l5)2+d(L0+Z-l5)+e=0

(20)

其中：

解式(20)可得：

(21)

即有：

Z=u+l5-L0

(22)

2.4 位置分析算例

設并聯機構結構參數為：l1=400 mm，l2=370 mm，l3=150 mm，l4=75 mm，l5=185 mm，l6=560 mm，l7=165 mm，l8=60 mm，l9=210 mm，L0=415 mm。根據三維建模與實際裝配情況，式(10)與式(21)中的符號“±”選“+”，式(17)與式(19)中的符號“±”選“-”，通過MATLAB[19-20]驗證所得位置正反解方程正確性。仿真步驟如下：

(1)設置輸入參數(X,Y,Z)；

(2)將輸入參數(X,Y,Z)代入正解模型，計算得正解參數(x,y,β)；

(3)將正解參數(x,y,β)代入反解模型，計算得反解參數(X′,Y′,Z′)；

(4)計算所得反解參數(X′,Y′,Z′)與輸入參數(X,Y,Z)的差值；

(5)根據差值判斷位置分析正確性。

經上述仿真步驟，可得位置分析算例，如表1所示：由正反解方程所得的反解參數(X′,Y′,Z′)與輸入參數(X,Y,Z)差值為0，即所得位置正反解方程正確。

表1 位置分析算例

3 工作空間

工作空間即滿足約束條件的機構末端參考點集，假設桿件在運動過程中不發生干涉，基于運動學正解，使用極限邊界法求解機構工作空間，具體步驟如下：

(1)根據第2.4節設置機構尺寸參數；

(2)設定驅動副輸入參數(X,Y,Z)的搜索區間為X∈[-100 mm,0]，Y∈[-250 mm,250 mm]，Z∈[-150 mm,150 mm]；

(3)由幾何約束，求解約束方程：

(4)將步驟(1)和步驟(2)代入位置正解方程中，求解動平臺位姿參數，并由步驟(3)所示的約束條件對位姿參數進行篩選。

依次重復步驟(1)—步驟(4)，并以步長ΔX、ΔY、ΔZ在驅動副行程內進行搜索，當到達驅動副行程邊界時結束，最后利用MATLAB軟件記錄并輸出所有滿足約束條件的點集，所得機構三維工作空間如圖3所示。

由圖3和圖4可知，在X∈[-100 mm,0]范圍內，y-β截面工作空間凹凸有界，邊界內部區域連續無空洞。隨著x值的增大，截面面積朝y軸正向逐漸增大。

圖3 并聯機構三維工作空間

圖4 工作空間y-β截面

4 解耦分析

4.1 耦合類型判斷

解耦即機構某方向的運動僅受特定方向的驅動影響，而其他方向的驅動不影響該方向的運動[21]。隨著運動支鏈的增多，機構耦合性增強，進而影響機構的控制，降低運動精度，因此解耦分析是必要的。

(23)

整理式(23)，基于Jacobian矩陣可得如下形式：

(24)

式中:Jp和Jq分別為該并聯機構的正、逆Jacobian矩陣。

且有：

Jp=

根據耦合特性，GOGU[22]將并聯機構分為4類：

(1)完全同性并聯機構：Jacobian矩陣J為對角矩陣，且對角元素相同；

(2)去耦并聯機構：Jacobian矩陣J為對角矩陣，但對角元素不同；

(3)解耦并聯機構：Jacobian矩陣J為三角矩陣；

(4)若非上述三類，則為耦合并聯機構。

由第1.2節和第2.1節可知，該并聯機構沿x、y、z軸的直線移動輸入(X,Y,Z)產生沿x、y軸的平移和繞y軸的轉動，使動平臺輸出三自由度運動(x,y,β)。在保證動平臺輸出運動(x,y,β)的前提下共有7種輸入-輸出控制方式：

(1)X-x，即保持輸入(Y,Z)不變，改變輸入X，研究輸入X與輸出x間的對應關系。

(2)Y-y，即保持輸入(X,Z)不變，改變輸入Y，研究輸入Y與輸出y間的對應關系。

(3)Z-β,即保持輸入(X,Y)不變，改變輸入Z，研究輸入Z與輸出β間的對應關系。

(4)(X,Y)-(x,y),即保持輸入Z不變，改變輸入(X,Y)，研究輸入(X,Y)與輸出(x,y)間的對應關系。

(5)(X,Z)-(x,β),即保持輸入Y不變，改變輸入(X,Z)，研究輸入(X,Z)與輸出(x,β)間的對應關系。

(6)(Y,Z)-(y,β),即保持輸入X不變，改變輸入(Y,Z)，研究輸入(Y,Z)與輸出(y,β)間的對應關系。

(7)(X,Y,Z)-(x,y,β),即同時改變輸入(X,Y,Z)，研究輸入(X,Y,Z)與輸出(x,y,β)間的對應關系。

由式(24)中的Jp可知，該并聯機構J矩陣屬于非對角、非三角矩陣，該機構為耦合并聯機構，即存在耦合輸入-輸出控制方式。

4.2 控制方式解耦分析

由式(24)的Jp可知，正Jacobian矩陣Jp的列反映輸入-輸出參數的映射關系。為進一步研究機構控制方式的解耦特性，根據Jacobian矩陣列的相關性[23]可知：

(25)

式(25)表示第i列與第j列向量所代表的輸入-輸出控制方式線性無關，即無耦合；

(26)

(27)

若G為對角矩陣，則機構輸入-輸出控制方式完全解耦；反之則存在耦合，對應輸入-輸出控制方式具有相關性。由式(27)可知：

5 速度與加速度正解分析

5.1 速度正解公式推導

當機構不存在奇異位置時，即Jp可逆，由式(24)可知，該并聯機構速度正解[24-25]為

(28)

5.2 加速度正解公式推導

將式(24)中各變量對時間求一階導數，可得：

(29)

其中:

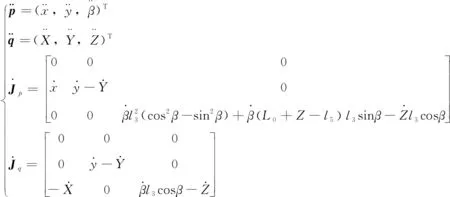
當機構不存在奇異位置時，即Jp可逆，則該并聯機構加速度正解為

(30)

5.3 速度與加速度仿真

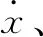
圖5 動平臺速度ADAMS仿真曲線

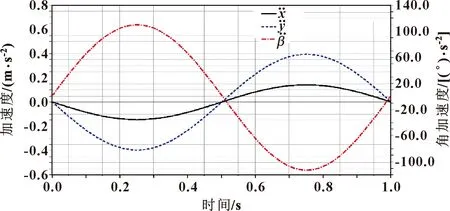
圖6 動平臺加速度ADAMS仿真曲線

由圖5和圖6可知:該并聯機構速度與加速度曲線變化平穩，無尖點，具有良好的動力學性能。

6 結論

(1)基于拓撲結構設計理論，提出一種新型2T1R弱耦合并聯機構，可實現動平臺沿x軸、y軸的平移和繞y軸的轉動。

(2)該并聯機構耦合度為1，降低了機構位置正解的求解難度，通過MATLAB仿真對比反解參數與輸入參數，二者差值趨于0,體現了位置分析的合理性。

(3)基于位置正解分析該機構的工作空間，發現其工作空間連續無空洞。

(4)基于Jacobian矩陣列的相關性，推得該機構平動輸入Y與平動輸出x間存在耦合，3種輸入-輸出控制方式X-x、Z-β和(X,Z)-(x,β)解耦。

(5)速度與加速度曲線變化平穩且無尖點，表明該并聯機構具有較好的動力學性能。