基于動態貝葉斯網絡的多狀態系統可靠性分析

齊金平，李少雄，周亞輝 ，王康

(1.蘭州交通大學機電技術研究所，甘肅蘭州 730070；2.甘肅省物流及運輸裝備信息化工程技術研究中心，甘肅蘭州 730070；3.甘肅省物流與運輸裝備行業技術中心，甘肅蘭州 730070)

0 前言

故障樹分析法(Fault Tree Analysis,FTA)是可靠性研究方法之一，已使用普遍，但其故障概率精確已知、邏輯門之間必須聯系明確等條件限制了它在可靠性分析以及故障診斷中的應用，T-S模糊故障樹既考慮到故障程度對系統的影響，也解決了事件之間的不確定性問題，但不能逆向推理。貝葉斯網絡(Bayesian Network，BN)的優勢在處理復雜系統可靠性問題時進一步凸顯，不僅廣受青睞，還得到了擴展，出現了離散、模糊、動態等貝葉斯網絡，相對于現存可靠性分析方法，BN層次清晰分明，推理關系明確，輔助軟件發展成熟，但建模相對困難。將兩種方法綜合求解，可將其建模推理優勢充分利用。

李興運、齊金平將T-S模糊故障樹轉化為BN解決了受電弓系統的多態性問題；任宇超等以聯接樹算法為基礎，對地鐵車門建立故障貝葉斯網絡,對其進行可靠性分析；張友鵬、解紹鋒等對不同的系統構建以故障樹為基礎的貝葉斯網絡，從而求解相關指標并尋出系統易故障部件。黃洪鐘等對太陽翼進行了動態故障樹分析(Dynamic Fault Tree Analysis，DFTA);房丙午等提出基于動態貝葉斯網絡(Dynamic Bayesian Network，DBN)的復雜系統定量分析；郭濟鳴等以制動系統為例，構建DBN進行可靠性分析。

以上方法都是單純的基于動態故障樹或離散BN的動態分析，無法刻畫出任意形式的失效行為，且難以反映可靠度與時間的函數關系。本文作者將基于沖激函數約束連續時間T-S動態故障樹，映射新型動態貝葉斯網絡，在GeNIe2.0軟件中搭建貝葉斯網絡模型，導出后驗概率，再計算合成動靜態模塊重要度，發揮兩者對復雜系統的建模與推理優勢，并為尋找系統薄弱環節提供依據，最后借助相關軟件仿真出系統的可靠度-時間變化曲線。

1 T-S模糊動態故障樹

T-S模糊動態故障樹區別于T-S模糊故障樹，它是基于動態門的時序邏輯關系構建，每條規則(=1,2,…,)為一個下級事件的故障時序。假設與分別表示(=1,2,…,)(下級事件)與(上級事件)故障時間和沖擊點時刻，=即與故障時間一致，則沖擊函數約束與的故障時間表達式(1)所示：

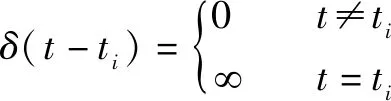
(1)

其中:表示事件，沖擊點的時刻為，當=，即(-)=∞時，故障后立刻故障。

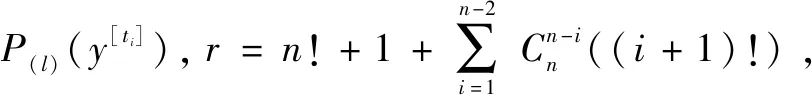
表1 T-S動態門的描述規則

2 新型模糊動態貝葉斯網絡

在靜態模糊BN中融入時間序列得到新型模糊DBN，基于第1節T-S模糊DFTA表述模糊DBN步驟如下：

(1)T-S模糊動態故障樹映射為模糊DBN，如圖1所示；

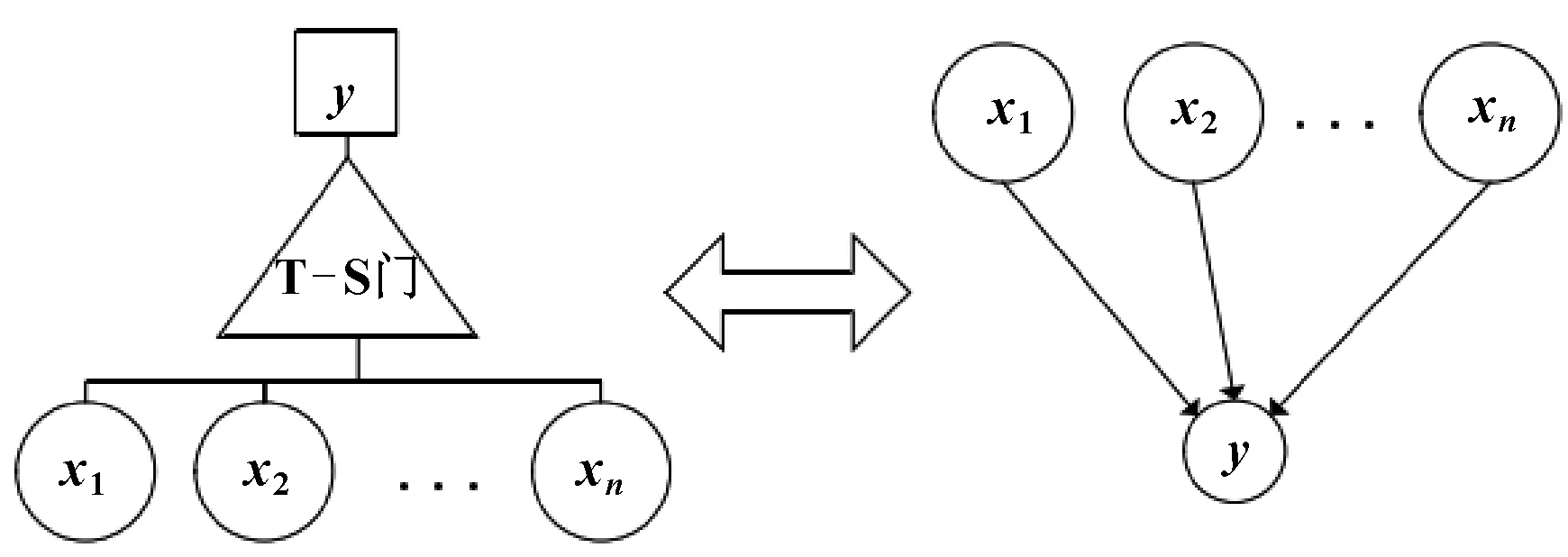
圖1 T-S模糊DFTA到模糊DBN映射圖

(2)動態門及規則對應表述條件概率表，具體如下：

若表示系統任務時間，以間隔=將總任務時間分為[0,),[,2),…,[(-1),),[,+∞)共段，記為時間段1,2,…,+1，假如父節點在時間段(=1,2,…,,+1)失效，子節點在時間段失效狀態為[]，則映射后的條件概率如表2所示。

表2 DBN條件概率

2.1 葉節點失效概率

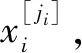
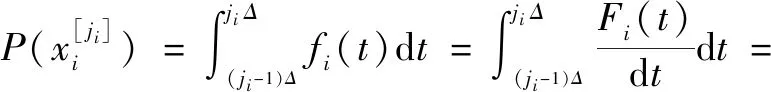
[exp()-1]exp(-)

(2)

式中:()為根節點的概率密度函數;()為根節點的不可靠度;為的失效率。

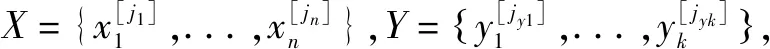
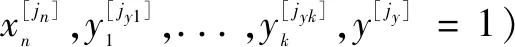
(3)

2.2 根節點后驗概率及重要度

根據貝葉斯網絡反向推理特點，若已知時間段的失效概率，可得根節點的后驗概率

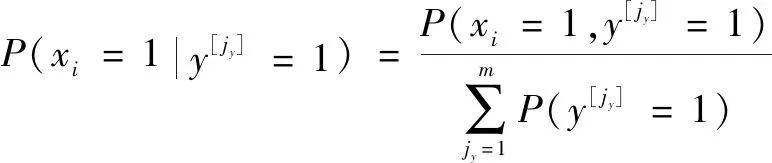
(4)

根據上式，可得根節點在任務時間失效的后驗概率為

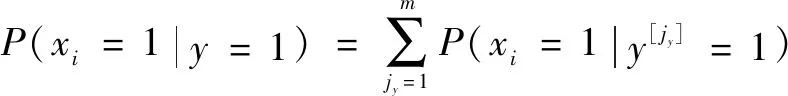
(5)

復雜系統中部件的重要性呈現非均等特性，重要度是可靠性分析中的一個重要指標，系統隨著根節點失效狀態的概率變化而變化的程度即為概率重要度，當葉節點在時間段內失效時根節點的概率重要度為

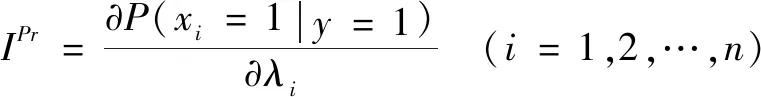
(6)

根節點在時間段內的概率重要度為

()=()·()

(7)

式中:()為每個底事件相對于系統的重要度;()為底事件對于子樹的重要度。

3 多狀態系統動態性可靠性分析

3.1 動車組空氣供給系統

以動車組空氣供給系統為例，對其可靠性分析。系統工作時，空壓機產生的壓縮空氣通過列車上的總風管傳輸，途經控制風管，至控制、制動風缸，如圖2所示。

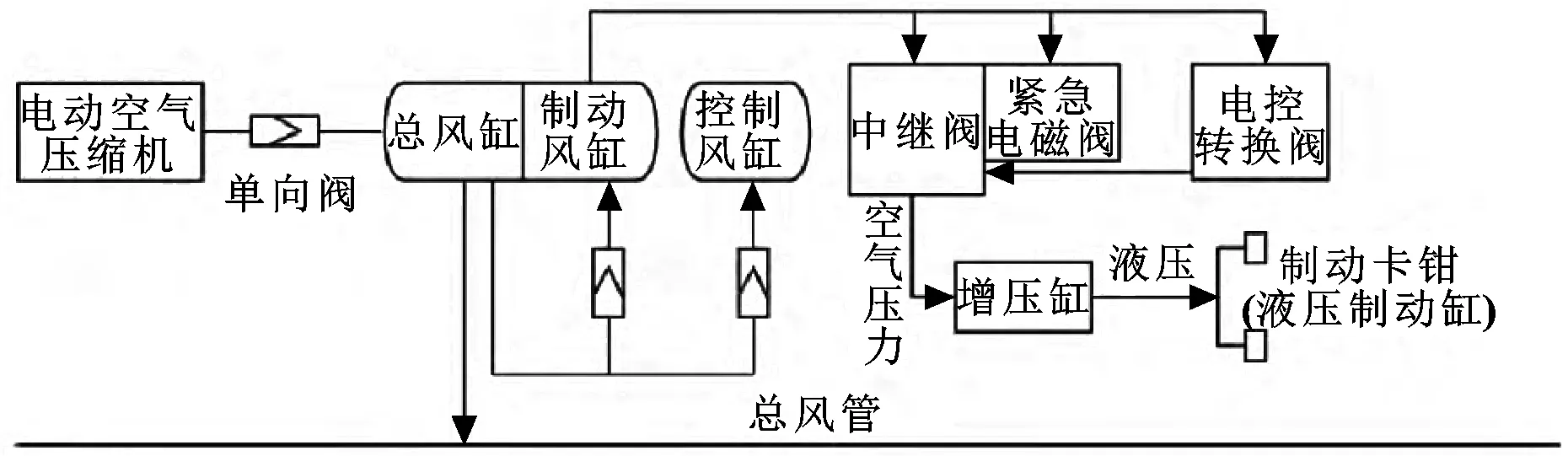
圖2 空氣供給系統簡圖

3.2 系統建模及可靠性分析

對某動車所動車組運行的歷史故障數據進行歸類、整理統計，綜合專家調查法與模糊數學知識分析處理，得到故障率較高的部件及其故障率，以其部件為底事件，以空氣供給系統為頂事件建立T-S模糊DFTA如圖3所示，事件名稱及模糊故障率如表3所示。

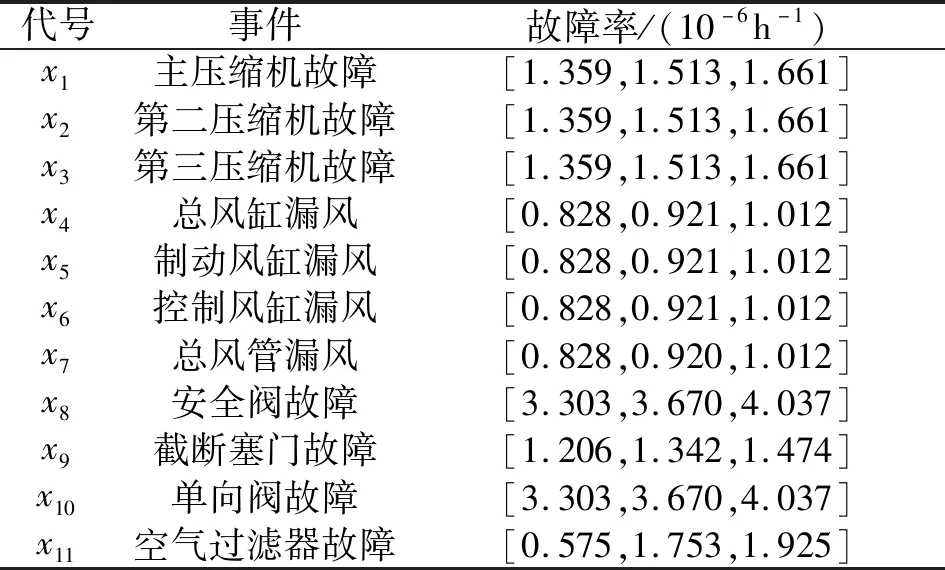
表3 事件代號及故障率

根據圖3所示的T-S模糊DFTA可得圖4所示的DBN圖。

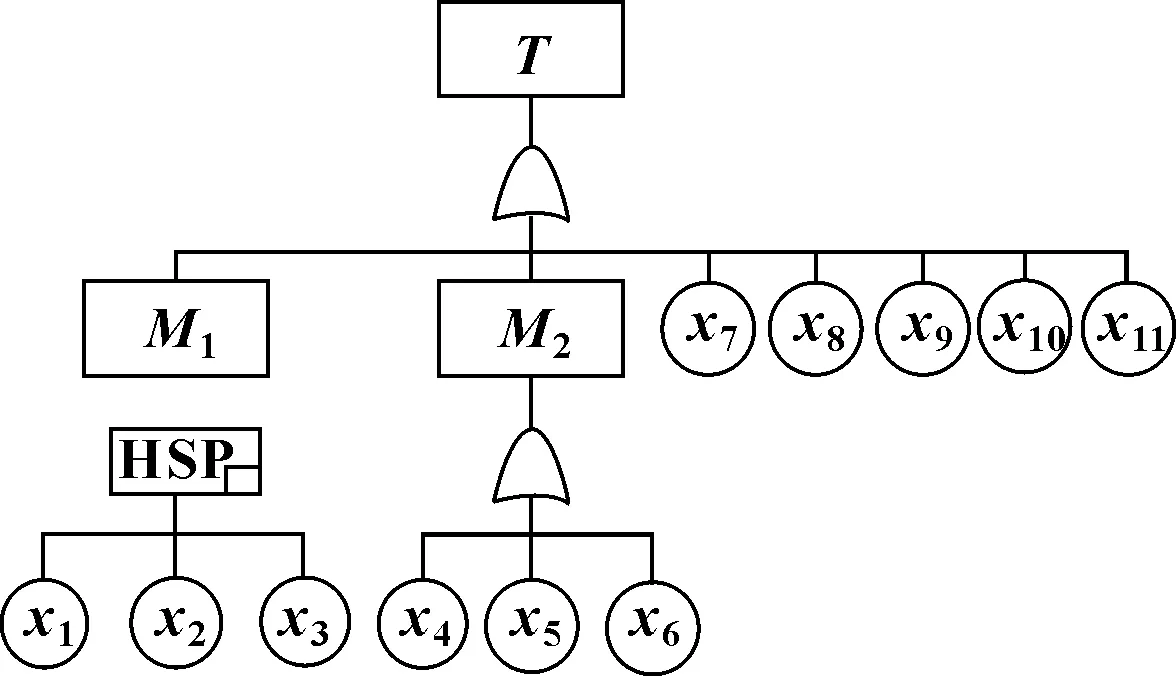
圖3 空氣供給系統故障樹

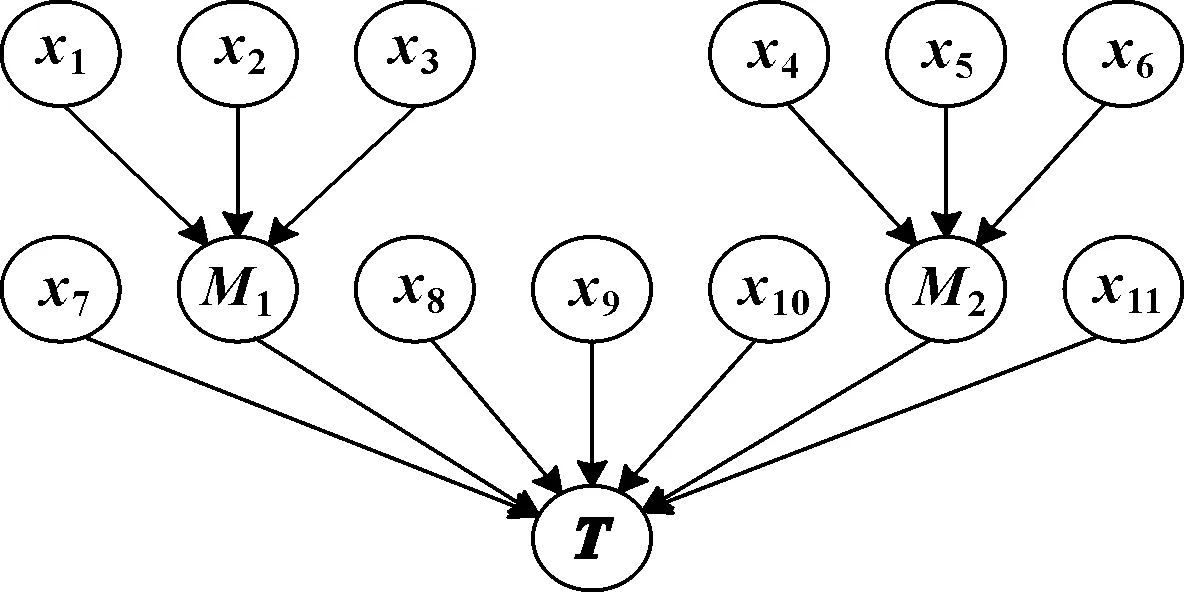
圖4 空氣供給系統DBN圖

假設任務時間為15 000 h，取=3 000 h，根據上述新型貝葉斯網絡方法，在GeNIe2.0軟件中繪制貝葉斯網絡，根據表2，得葉節點故障概率如表4所示，用模型導出后驗概率，根據式(6)(7)計算根節點相對于葉節點的重要度，數值如圖5所示。

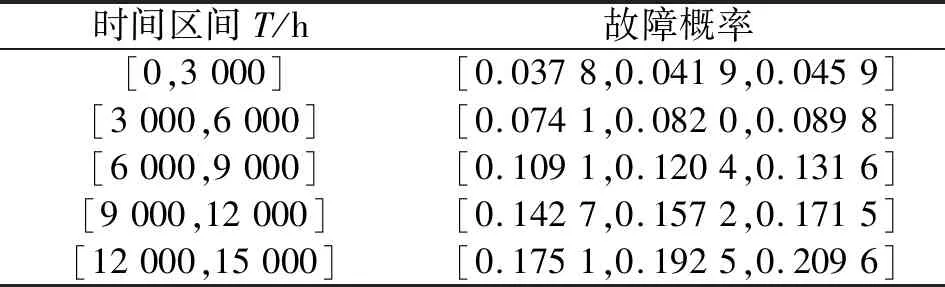
表4 葉節點故障概率

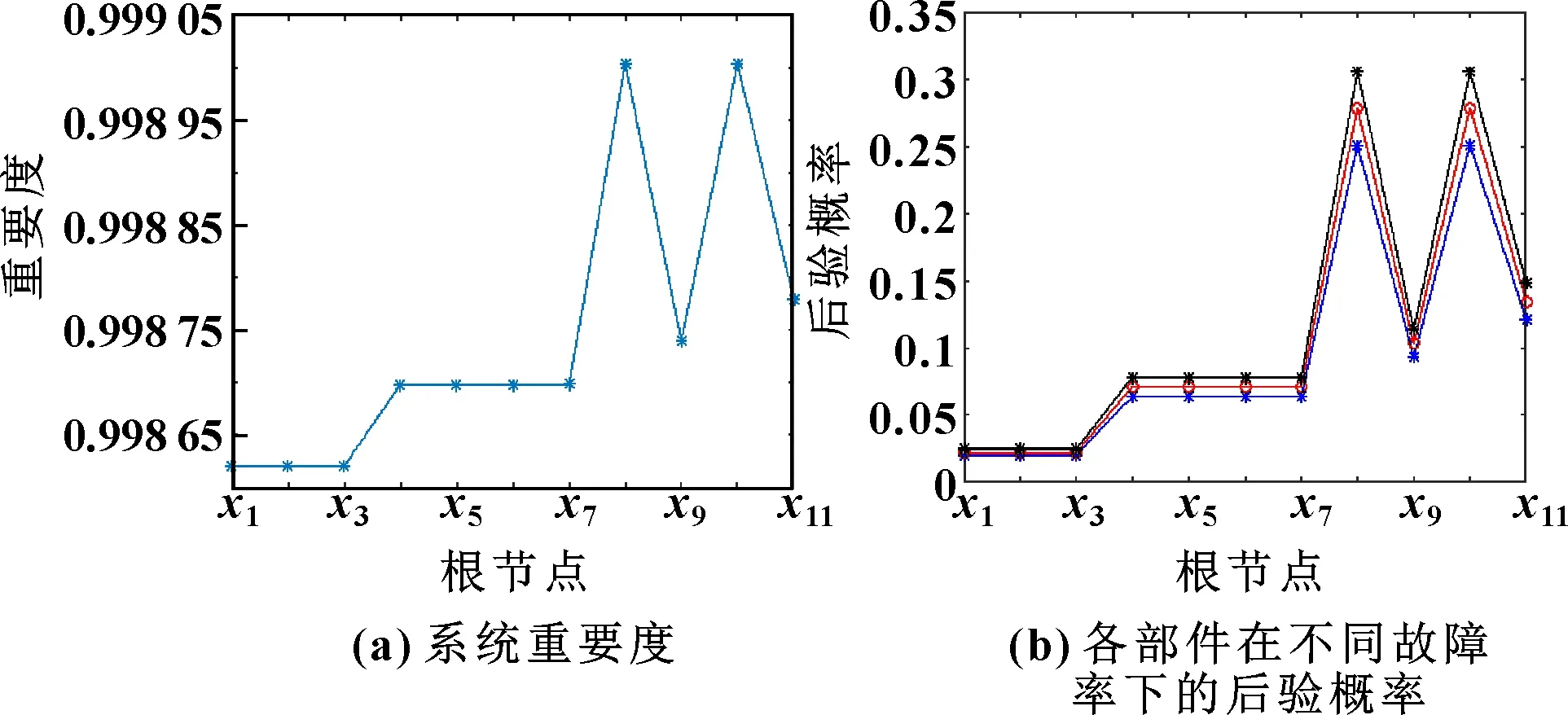
圖5 系統重要度與后驗概率分布

由圖5可知，安全閥()與單向閥()為系統的薄弱環節，若失效對系統的可靠度影響較大，應加大檢查檢修頻次，其余部件可參考圖示結果合理安排設備維護頻次。

根據文獻[14-15]，假設～均服從指數分布，在MATLAB軟件中編程仿真得系統可靠度變化曲線如圖6所示。可知:系統可靠度時間曲線縱向間距與時間保持正相關，這是因為部件隨著使用時間的增加，其可靠度的不確定性隨之變大。

圖6 系統可靠度變化曲線

4 結論

(1)新型動態貝葉斯網絡的提出，既發揮了連續時間T-S模糊動態故障樹的動靜態描述能力，又發揮了貝葉斯網絡的雙向推理建模與可描述動態優勢。基于沖激函數約束的連續時間T-S動態故障樹映射貝葉斯網絡，也解決了直接建立復雜貝葉斯模型的難題。

(2)以動車組空氣供給系統為例對其可靠性分析，原始的貝葉斯網絡模型只能分析故障的單一狀態，通過考慮故障的多態性，本文作者結合模糊數學理論建立模糊貝葉斯網絡模型，能夠同時分析故障的多態性和動態性。

(3)計算葉節點的故障概率，并通過仿真分析，得到動車組空氣供給系統隨時間變化時根節點的后驗概率以及重要度，并于軟件中仿真出可靠度-時間的變化曲線。