基于流-固耦合的測量耙設計

賈文杰， 孫科， 宋江濤， 牛文敬

(中航工業中國飛行試驗研究院， 西安 710089)

在航空發動機飛行試驗中，通常需要使用壓力和溫度測量耙測量發動機流道內的各種壓力和溫度信號，通過當地的總壓、靜壓、流動方向和溫度等數據來確定發動機的各個性能參數，因此測量耙的設計具有重要的意義。

航空發動機流道參數測量主要通過測量耙來實現[1-2]。目前，針對測量耙的結構強度設計與數值仿真方法已經有了較多的研究。陶冶等[3-4]、田琳等[5]已經針對測量耙的模態特性、動態特性和應力分布特性展開了相應的研究；李秋鋒等[6]研究了不同結構的測量耙對發動機流場參數的影響。目前國內外針對測量耙的研究已經較為成熟，并制定了相應的規范和標準[7-9]。國內測量耙的設計流程為：首先設計出測量耙的基本結構，然后通過有限元方法進行靜強度計算、模態分析和根據《軍用裝備實驗室環境試驗方法 振動試驗》(GJB 150.16A)中渦輪發動機振動環境功率譜密度進行隨機振動分析，考核測量耙的強度能否滿足要求。但在某型號發動機外涵出口測量耙設計過程中，發現通過有限元計算得到的靜應力與隨機振動應力遠遠超過該溫度下的材料許用應力，經過理論分析，并結合以往類似工況下的測量耙設計方案，發現這是由于現有測量耙設計方法及計算方法存在的不足所導致的，經過分析，現有的設計方法存在以下幾點問題：一是靜強度計算中，使用測量耙安裝截面的動態壓力作為均布面壓力載荷，模擬測量耙迎風面受到的氣動載荷，但實際上測量耙在流道的受力可以近似為圓柱繞流問題[10-11]，測量耙無法將氣流完全滯止在耙體前方，現有的加載方式與測量耙實際受力條件相差較大，導致靜強度計算結果可靠性較低。二是模態分析時，未考慮測量耙所受氣動力、溫度載荷等預應力對測量耙模態特性的影響。現有研究表明，結構受到不可忽略的應力載荷時，模態會發生變化，即“模態預應力效應”[12]。測量耙安裝在發動機流道內部，受到沿來流方向的氣動力和流場中內外涵溫度不均勻帶來的熱應力，模態特性與靜止大氣環境中的不同。三是在實際的環境試驗中，常規的掃頻試驗無法準確模擬測量耙在真實流道內所受的氣動力與熱載荷下的頻率，現有的試驗方法也很難模擬真實裝機狀態下的測量耙模態特性和所受應力載荷。

為解決現有設計方法中存在的不足，現綜合考慮測量耙所處的流場參數對測量耙強度和模態特性的影響，模擬測量耙在流場中所受到的真實載荷，選擇采用單向流-固耦合方法進行測量耙強度計算，以提高現有測量耙設計水平，并應用于后期測量耙設計中。

1 理論分析

流固耦合方法主要用于研究固體在流場作用下的受力以及固體位移對流場產生的影響[13-14]，主要分為單向流固耦合和雙向流固耦合，其中雙向流固耦合適用于流場產生的載荷使固體結構產生較大的變形，從而對流場分布產生影響的算例中，雙向流固耦合計算精度較高，但占用的計算資源較大且收斂緩慢；單向流固耦合適用于固體域形變較小，且對流場帶來的影響較小的工況，所用計算資源小且容易收斂，在小變形條件下有著較好的計算精度，考慮到測量耙通常由高強度鋼或高溫合金制成，安裝在發動機流道中變形較小，因此選用單向流固耦合方法進行研究，以下流固耦合均指單向流固耦合。

在流固耦合計算過程中，流體計算域通過流固耦合交界面實現與固體計算域之間的數據傳遞，因此在流固耦合交界面上需要保持位移、應力、熱流量以及溫度等變量之間的協調性，以保證數據傳遞的可靠性，需滿足以下4個守恒方程[15]，即

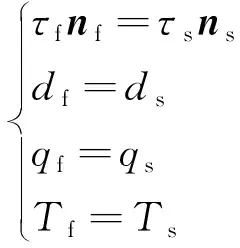
(1)

式(1)中：τ為應力；n為法向量；d為位移；q為熱流量；T為溫度；下標f為流體計算域，s為固體計算域。

考慮到熱應力和氣動力對測量耙模態特性的影響，在結構面上附加一個預應力剛度矩陣，結合幾何非線性問題中的有限變形理論，采用拉格朗日坐標系中的增量位能原理，建立有限元方程，將這些影響因素轉換為測量耙結構的預應力剛度矩陣，并將其疊加到結構的剛度矩陣上，最后生成考慮預應力和流固耦合的方程[16]，具體為

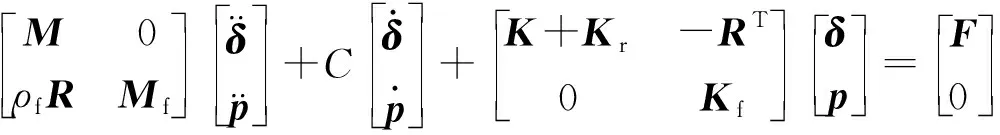
(2)

式(2)中：M為結構質量矩陣；Mf為流體等效質量矩陣；ρf為流體密度；R為流固耦合矩陣；C為阻尼；K為結構剛度矩陣；Kr和Kf分別為預應力剛度矩陣及流體等效剛度矩陣；F為結構外載荷；p為流體壓力；δ為結構位移，上標一個點和兩個點分別表示該參數的一階導和二階導。

求解上述問題時，首先進行靜態條件下的線性應力分析，將外部載荷轉化為結構的額外剛度。靜態分析時不考慮阻尼，且不考慮自由流場中流體的位移帶來的壓力變化，即

Kσθ=F

(3)

然后，基于靜態分析的應力位移σθ獲得預應力等效矩陣S，結合預應力等效矩陣并忽略阻尼，得到測量耙的模態方程為

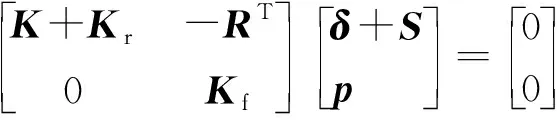
(4)

2 仿真計算

2.1 模型介紹

圖1(a)所示為某型發動機外涵出口總溫總壓測量耙在發動機流道中的裝配圖，測量耙使用外裝方式固定在發動機混合器機匣壁面上，在內涵機匣波瓣混合器上留有跑道形的安裝孔，測量耙通過該跑道形的小孔伸入內涵流道中，波瓣混合器幾何結構如圖1(b)所示。

對上述模型進行單向流固耦合計算，考慮到計算資源的合理分配，對計算域進行如下簡化。

(1)測量耙在加工過程中內部鋪設有引氣管路及相關附件，在測量耙模型中對其管路結構進行了相應的簡化。

(2)發動機機匣和波瓣混合器均為圓柱形中心對稱結構，為節約計算資源，取發動機流道1/8扇段進行研究。采用的計算流程如圖2所示。

2.2 流場分析

首先對測量耙進行流場分析，使用的計算流體動力學(computational fluid dynamics，CFD)流場計算軟件為Fluent，使用壓力求解器，湍流模型為Standardk-ε，近壁面處使用標準壁面函數，求解采用SIMPLEC方法，使用壓力進口和壓力出口邊界條件，進出口條件參數如表1所示。選用四面體網格進行網格劃分，經過網格無關性驗證，最終選擇的流場計算域網格數量為320萬。

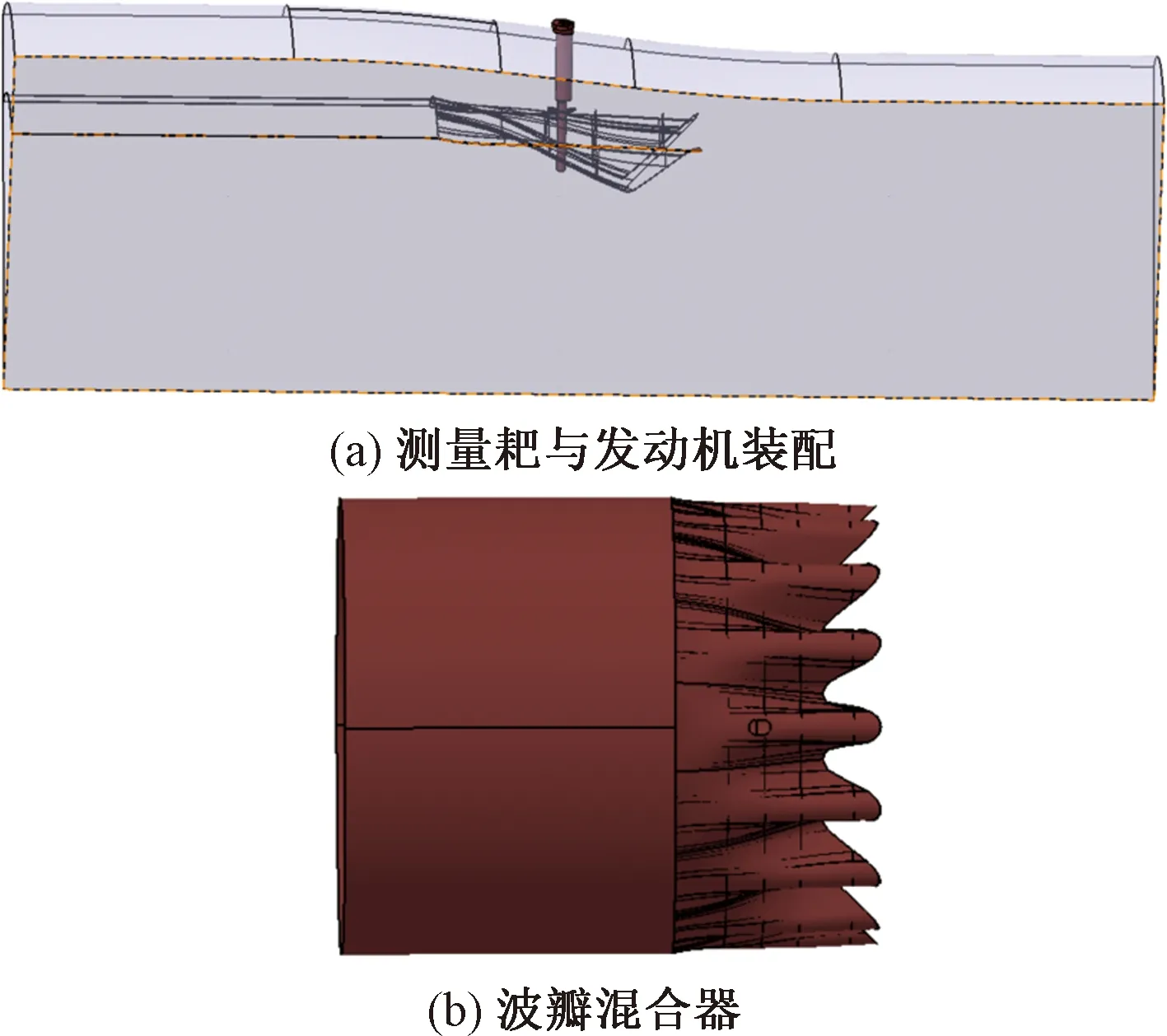
圖1 計算模型介紹Fig.1 Introduction to calculation model

如圖3(a)所示為流場計算得到的測量耙表面壓力分布云圖，圖3(b)為采用傳統方法進行靜強度計算時對測量耙迎風面施加的均布面壓力載荷。可

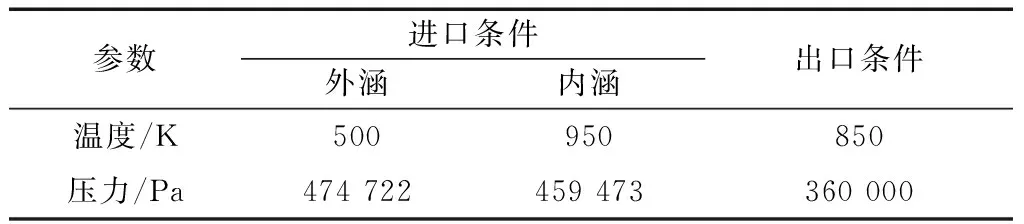
表1 進出口參數

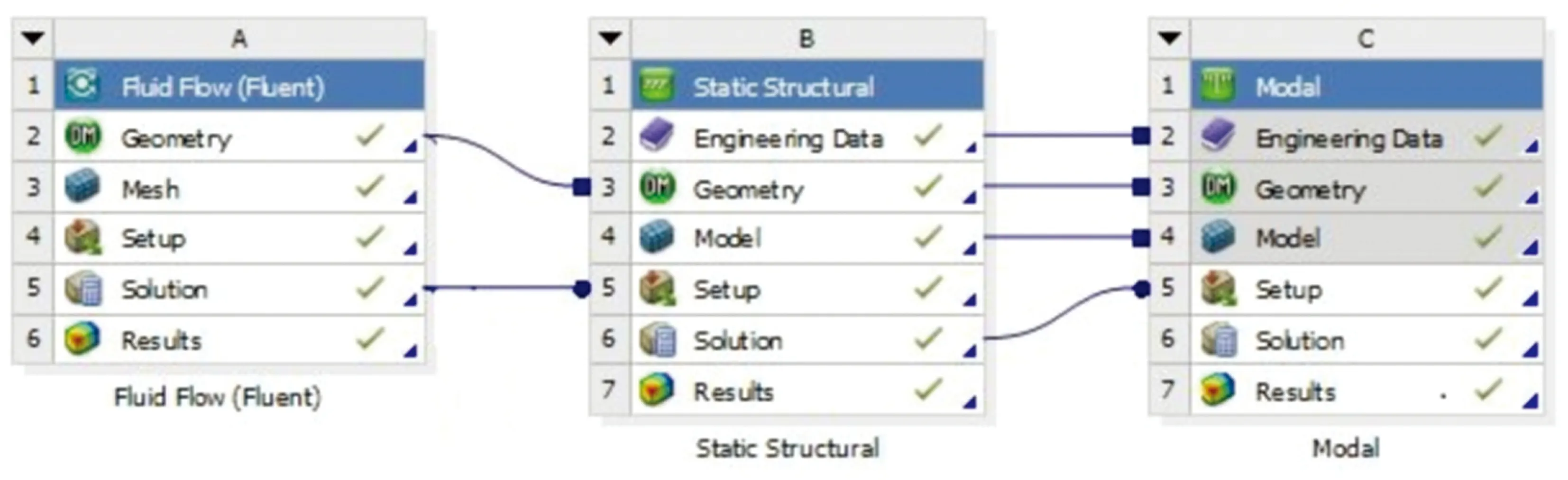
圖2 流固耦合計算流程示意圖Fig.2 Schematic diagram of coupling calculation process

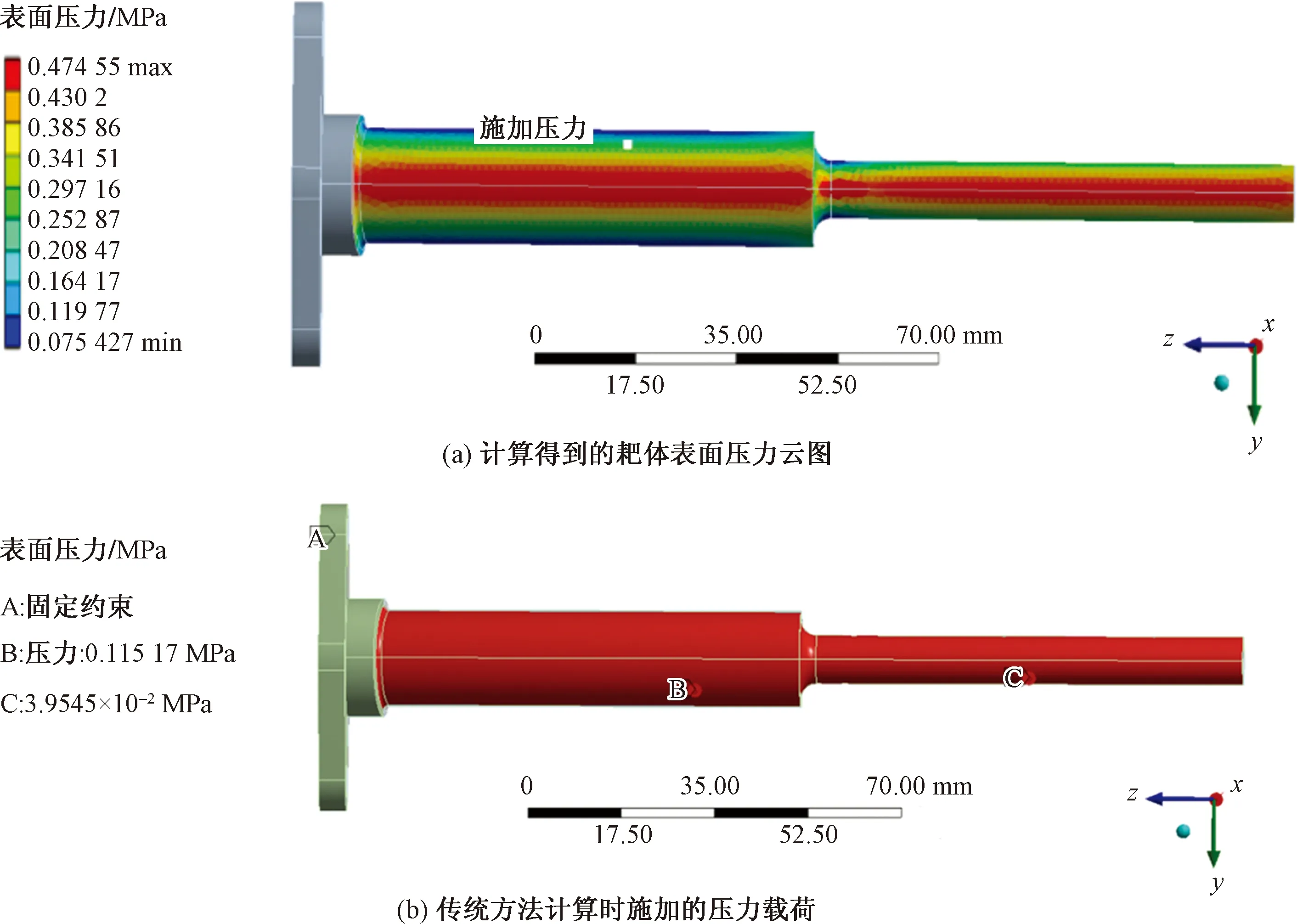
圖3 測量耙表面壓力載荷云圖Fig.3 Pressure contour of the rake surface

以看出，這與流場計算得到的測量耙表面真實受力有很大不同，在實際的發動機流道中，測量耙迎風面的壓力載荷并非均布載荷，靠近耙體中心位置可以完全滯止氣流，因此壓力最大；氣流從耙體兩側流過，因此迎風面兩側壓力較低，這與現有圓柱繞流中的研究結果相符。

2.3 靜強度分析

測量耙耙體暴露在外涵和內涵流道中，內外涵溫度和壓力差別較大，因此受到熱載荷與氣動壓力載荷，將流場計算得到的壓力載荷與溫度載荷作為輸入參數，進行氣動載荷分析。該測量耙由GH4169材料制成，材料密度為8 240 kg/m3，熔化溫度范圍為1 260～1 320 ℃，各溫度下彈性模量E及泊松比μ如表2所示，雙真空熔煉的圓餅鍛件持久強度如表3所示。

在ANSYS中進行分析，采用以四面體為主的網格劃分方法，共劃分402 446個網格節點，確保有限元網格尺寸與流場計算中流固耦合面的網格尺寸完全相同。圖4為耙體溫度分布，可以看出，測量耙內涵部分和外涵部分溫度相差較大，考慮到發動機內涵熱變形，波瓣混合器上預留的跑道型孔尺寸大于測量耙內涵部分直徑，導致有一部分內涵高溫氣體流入外涵，因此測量耙過渡段背風面存在局部高溫區。結合表3中不同溫度下材料的持久強度變化可以看出，溫度對測量耙的影響無法忽略，原有靜強度計算方法存在顯著不足，流固耦合方法更能準確模擬測量耙真實的受力情況。

表2 GH4169材料不同溫度下的彈性模量和泊松比

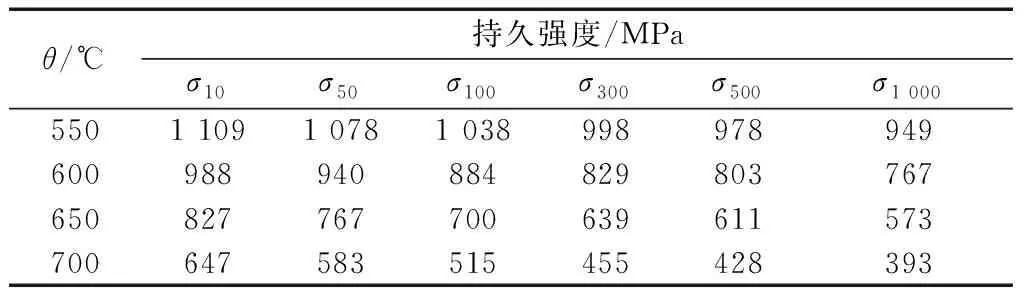
表3 GH4169材料持久強度

從表4中可以看出，兩種方法靜強度計算結果相差較大，靜應力由248.69 MPa減小為51.49 MPa，變形由0.81 mm減小為0.16 mm，分析原因如下。

(1)原有計算方法中假設氣體被測量耙完全滯止，因此在靜強度計算時施加的壓力載荷過大。

(2)原始方法不考慮熱應力的影響，考慮到測量耙的安全裕度，計算時一般通過插值得到測量耙在流場最高溫度下的彈性模型、泊松比等材料屬性，過于保守導致材料本身強度較低。

經過對比，可以看出流固耦合方法在測量耙靜強度計算方面效果更優。

表4 靜強度及變形分布

2.4 模態分析

測量耙安裝于發動機流道內，受到發動機轉子所產生的振動載荷，當測量耙的固有頻率和氣流的激振頻率或轉子的轉動頻率重合時，就會產生諧共振，造成耙體的損壞，因此需要進行模態分析，確保測量耙頻率可以避開發動機轉子固有頻率。

將前文計算得到的靜應力作為預應力，開展預應力載荷下的測量耙模態分析，表5為采用原有設計方法和流固耦合方法計算得到的模態對比，可以看出，采用流固耦合方法計算得到的測量耙前兩階固有頻率分別提高了13.96%和11.9%，分析原因可能是由于原有方法未考慮測量耙在實際流場中受到的氣動力對模態的影響，以及兩種計算方法中材料參數設置的不同導致。采用流固耦合的方法可以更加真實的模擬測量耙在發動機流道內所受的熱載荷和氣動載荷。

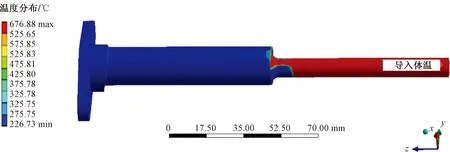
圖4 耙體溫度分布云圖Fig.4 Temperature contour of the rake

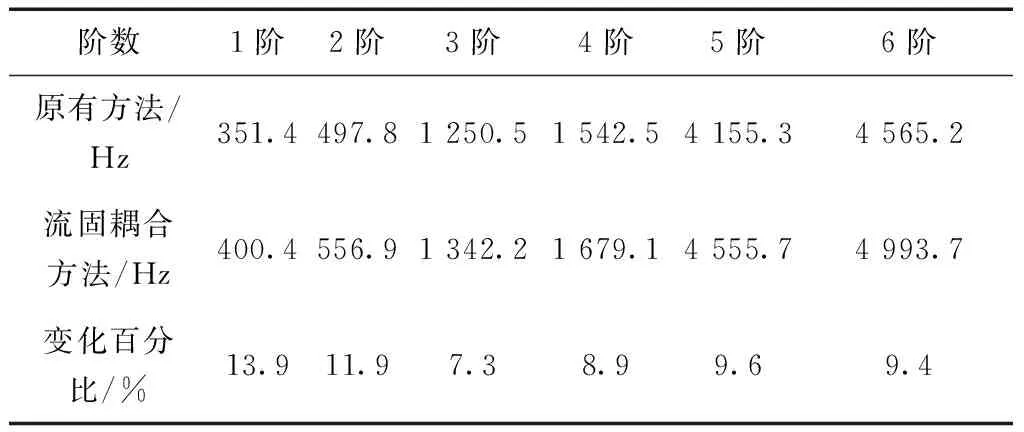
表5 兩種方法計算模態結果對比

3 結論

針對現有測量耙設計方法中存在的不足，提出采用流固耦合的方法開展測量耙在流場中的氣動載荷分析，然后以流場分析的結果作為輸入參數進行測量耙的模態特性分析，結論如下。

(1)原有方法進行靜強度計算時，將測量耙安裝截面動壓作為均布載荷施加在耙體迎風面上，這與實際裝機狀態相差較大，原有模態計算方法未考慮氣動力等預應力對測量耙模態特性的影響，導致計算結果誤差較大。

(2)采用流固耦合方法進行計算，將CFD流場計算的溫度和壓力載荷作為靜強度輸入參數，與傳統方法對比發現，靜應力由248.69 MPa減小為51.49 MPa，變形由0.81 mm減小為0.16 mm。

(3)將計算得到的靜應力作為預應力進行模態分析，與原有方法相比，前六階模態均增長超過7%，分析是由于傳統測量耙設計方法不能準確模擬測量耙真實的裝機狀態，且設計方法過于保守，導致計算得到的靜應力偏大，模態值偏低。

(4)考慮到流固耦合方法在渦輪葉片設計等領域已經有了越來越廣泛的應用，其可靠性已經得到充分驗證，因此流固耦合設計方法可以為提高現有的測量耙設計能力提供參考，同時應用于后續測量耙設計及校核計算中。