考慮磁性顆粒不均勻分布的磁流變液修正微觀力學模型及試驗驗證

楊 楊，徐趙東

(東南大學混凝土與預應力混凝土結構教育部重點實驗室，南京 210096)

磁流變液是一種典型的智能可控材料，由載液、磁性顆粒和各種添加劑混合而成[1]。磁流變液最顯著的特征是，在外加磁場的作用下，它可以在毫秒內從牛頓流體變成類固體，而且磁場撤銷后，又可以瞬間恢復原狀。這種磁致效應從微觀角度可以解釋為，在沒有磁場干擾的情況下，磁流變液中的磁性顆粒不受約束，磁流變液處于自由流動狀態；而在施加磁場后，磁性顆粒會快速沿磁場方向形成鏈狀和柱狀結構，磁流變液的流動需要剪切磁鏈，在宏觀上就表現為剪切應力顯著增大[2]。

剪切屈服應力是衡量磁流變液磁致效應高低的指標，也是磁流變液區別于普通液體的重要力學特征。為了描述剪切屈服應力隨磁感應強度和剪切速率的非線性變化關系，研究人員提出了很多不同的磁流變液力學模型。早期的磁流變液力學模型都是宏觀現象模型，如Bingham 模型，雙黏性模型Herschel-Bulkley 模型等[3-5]。宏觀力學模型形式簡單，但是不能反映磁流變液微觀結構參數對剪切屈服應力的影響。因此，很多學者開始致力于磁流變液微觀結構的分析，提出了各種考慮磁流變液微觀結構參數的力學模型。現有關于磁流變液微觀結構的研究都是基于磁偶極子理論，研究磁性顆粒在磁場作用下的成鏈與剪切斷裂等變化。SHULMAN 等[6]假設作用在磁化顆粒上的力矩等于磁矩，推導出了磁流變液剪切屈服應力的計算公式。PENG 等[7]基于磁鏈與磁場方向的夾角服從正態分布的假設，考慮了磁感應強度、磁性顆粒尺寸、體積分數、剪切應變速率和飽和磁化強度對磁流變液力學性能的影響，提出了磁流變液的微觀-宏觀交叉尺度模型。LIU 等[8]基于磁偶極子理論，分析了磁鏈在三種不同狀態下的力學性能，提出了磁流變液在受壓狀態下的微結構模型。李杰如等[9]對磁性顆粒進行微觀受力分析，對顆粒的鏈化與剪切過程進行數值模擬，建立了磁流變液微觀數值模型。姬晨等[10]基于分子動力學理論研究了磁鏈結構在外加磁場和驅動力作用下的變化規律。XU 等[11]假設磁流變液中磁性顆粒在磁場作用下呈初始傾斜的單鏈分布，提出了磁流變液初始傾斜單鏈模型。在單鏈模型基礎上，XU 等[12]從磁偶極子能量的角度出發，考慮相鄰磁鏈間的相互作用，推導了磁流變液雙鏈微觀結構的力學模型。在雙鏈模型基礎上，孫春麗[13]進一步考慮到磁流變液中磁鏈從單鏈到雙鏈的過渡和轉變，系統地提出了磁流變液單-雙鏈微觀力學模型。

總結現有的微觀力學模型可以發現，這些力學模型綜合考慮了磁流變液的各項微觀結構參數，在高磁感應強度下基本可以準確預測磁流變液的剪切屈服應力。然而，先前學者在推導磁流變液微觀模型時都假設相鄰鐵磁顆粒的間距是完全相等的且不隨磁感應強度而改變的，這與磁性顆粒分布的實際情況存在較大的偏差。從模型計算結果來看，當磁感應強度較低時，現有模型存在高估了磁流變液剪切屈服應力的缺點。因此，本文對磁性顆粒均勻分布這一假設進行修正，以提高微觀力學模型對磁流變液剪切屈服應力預測的準確性。本文假設相鄰磁性顆粒的間距服從卡方分布，并在現有的磁流變液雙鏈模型中引入分布系數來定量描述磁性顆粒的間距隨磁感應強度的變化關系，得到了基于磁性顆粒卡方分布的修正微觀力學模型。將本文提出的修正微觀力學模型帶入磁流變阻尼器的準靜態模型計算得到的阻尼器最大出力，和磁流變阻尼器性能試驗數據進行對比，驗證了本文提出的磁流變液修正微觀力學模型的有效性。

1 基于卡方分布的磁性顆粒不均勻分布假設

目前常用的磁流變液微觀力學模型主要有前文概括的單鏈模型、雙鏈模型和單-雙鏈模型。單鏈模型、雙鏈模型和單-雙鏈模型的共同點是模型的推導都基于一個假設，即同一條磁鏈上的磁性顆粒間距相等，均勻分布。如圖1 所示，磁性顆粒的間距d是一個固定值，即模型的建立是基于磁性顆粒均勻分布，且顆粒間距不隨磁感應強度的改變而變化的假設。然而，真實情況是在磁場作用下，磁性顆粒并不是均勻分布的，而且隨著磁感應強度的變化，磁性顆粒的間距也會隨之改變。從現有模型計算值和磁流變液性能試驗數據的對比來看[13-14]，當磁感應強度較低時，基于磁性顆粒均勻分布的力學模型都高估了磁流變液的剪切屈服應力。產生誤差的原因在于，當磁感應強度較低時磁性顆粒的分布不均勻性很強，而磁性顆粒均勻分布的假設就會導致計算得到的磁流變液剪切屈服應力大大超出實際值。同時，隨著磁感應強度的增強，磁性顆粒的間距會逐漸減小，而現有微觀模型中的磁性顆粒間距d被假定為固定值，并不會隨著磁感應強度而改變，從而進一步增大了模型計算值與實際值之間的誤差。

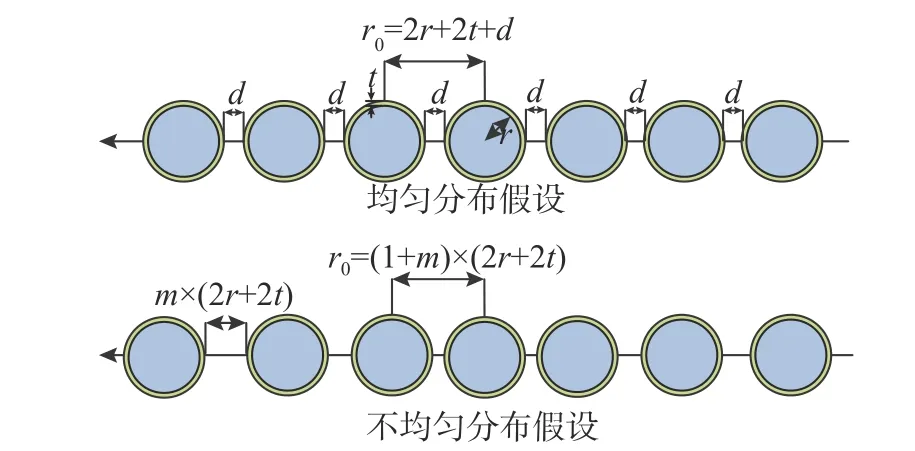
圖1 磁性顆粒均勻分布假設和不均勻分布假設Fig. 1 Even and uneven distribution hypotheses of magnetic particles

因此，很有必要對現有的基于磁性顆粒均勻分布假設的磁流變液微觀力學模型進行修正，將磁性顆粒的不均勻分布考慮進去。根據對磁流變塑性體微觀力學模型的研究[15]，在外加磁場作用下，磁性顆粒會呈現偏峰分布。基于磁性顆粒卡方分布假設的模型可以很好地描述磁流變彈性體的剪切屈服應力。本文借鑒這一假設，用卡方分布來描述磁流變液中磁性顆粒的不均勻分布，假設相鄰磁性顆粒的間距服從χ2分布，對磁流變液雙鏈微觀力學模型進行修正。

引入隨機變量m來表示磁性顆粒間距的不確定性，如式(1)和圖1 所示，r0為相鄰磁性顆粒的中心距，d為相鄰磁性顆粒凈距，t為包覆層厚度，r為顆粒半徑。m是一個大于等于0 的隨機變量。當其等于0 時，表示兩個磁性顆粒互相接觸。m越大，表示兩個磁性顆粒的間距越遠。假設m-χ2(n)，即相鄰磁性顆粒的間距服從卡方分布。卡方分布中的n是隨機變量m的期望值，如式(2)所示。分布參數n能反映相鄰磁性顆粒間距的平均密集程度，n越小，磁流變液中的磁性顆粒越密集。同時，n是一個與外加磁感應強度有關的參數，磁感應強度增大，n減小，磁性顆粒分布越密集。本文通過引入分布參數n，考慮了磁性顆粒分布的不均勻性以及顆粒間距隨磁感應強度的變化對磁流變液剪切屈服應力的影響，彌補了現有微觀力學模型中磁性顆粒均勻分布假設的不足。

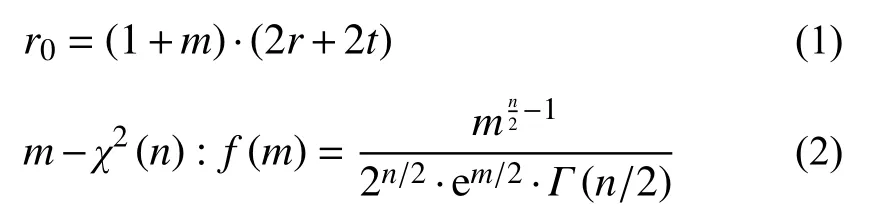
單鏈模型忽略了相鄰磁鏈的影響，計算結果低于實際剪切屈服應力；而單-雙鏈模型形式過于復雜，待定參數需要大量試驗數據確定。因此本文以準確性和實用性較為平衡的雙鏈微觀模型為基礎，研究考慮磁性顆粒不均勻分布的磁流變液微觀力學模型。基于式(1)和式(2)的磁性顆粒卡方分布假設，結合磁流變液雙鏈微觀力學模型，推導考慮磁性顆粒不均勻分布的磁流變液微觀力學模型。

將磁性顆粒看成磁偶極子，磁性顆粒i在外加磁場作用下的偶極距為：

2 考慮顆粒不均勻分布的磁流變液力學模型

2.1 模型推導

根據耦合場理論[14]，單條磁鏈中的單個磁性顆粒產生的磁偶極距包括外加磁場強度產生的偶極距和該磁鏈中其余顆粒磁化后產生的磁場強度導致的偶極距，如下式：

式中：m為磁鏈中單個磁性顆粒的磁偶極距(假設磁鏈中所有顆粒磁偶極距相等)；H0為磁鏈中顆粒受到的外加磁場強度； θ為磁鏈與外加磁場方向的夾角。

將本文提出的磁性顆粒卡方分布假設引入，即將式(1)代入式(5)，可以得到考慮磁性顆粒不均勻分布的單個磁性顆粒的磁偶極距：

得到單個磁性顆粒的總磁能后，對其進行求導得到雙鏈結構的剪切屈服應力。再對單位面積內所有雙鏈結構的剪切屈服應力求和，即可得到磁流變液的剪切屈服應力，如式(10)。具體推導過程與雙鏈模型一致[13]，本文不再贅述。

w(n)是本文引入的分布函數，表示磁性顆粒不均勻分布對磁流變液剪切屈服應力的影響。在低磁感應強度下，磁性顆粒分布十分不均勻，顆粒間距服從卡方分布。隨著磁感應強度的增大，磁性顆粒的分布逐漸均勻，相鄰磁性顆粒的間距不斷減小并趨于穩定。式(13)即是本文提出的磁流變液的修正雙鏈微觀力學模型，考慮了磁性顆粒的不均勻分布以及顆粒間距隨磁感應強度的變化對剪切屈服應力的影響。該模型綜合考慮了磁性顆粒不均勻分布、鄰鏈影響、磁感應強度、磁性顆粒體積分數、磁性顆粒尺寸和包覆層厚度等微觀結構參數對磁流變液剪切屈服應力的影響。

分布函數w(n)中顆粒間距隨磁感應強度的變化是通過分布參數n來體現的，n表示磁性顆粒分布的密集程度。分布參數隨磁感應強度的變化關系與磁流變液具體類型相關，需要磁流變液性能試驗數據來進行擬合。本文研究對象為論文[13]中制備的混合包覆磁流變液，該磁流變液基本參數如表1。選取磁性顆粒體積分數為35%和40%下的剪切屈服應力數據進行計算，可以得到不同磁感應強度下的分布參數，列在表2。需要說明的是，體積分數為35%和40%情況下，分布參數幾乎一致，說明在一定的體積分數范圍內，體積分數對分布參數的影響可以忽略。因此本文主要研究磁感應強度對分布參數的影響。

表1 磁流變液基本參數Table 1 Basic parameters of MR fluid

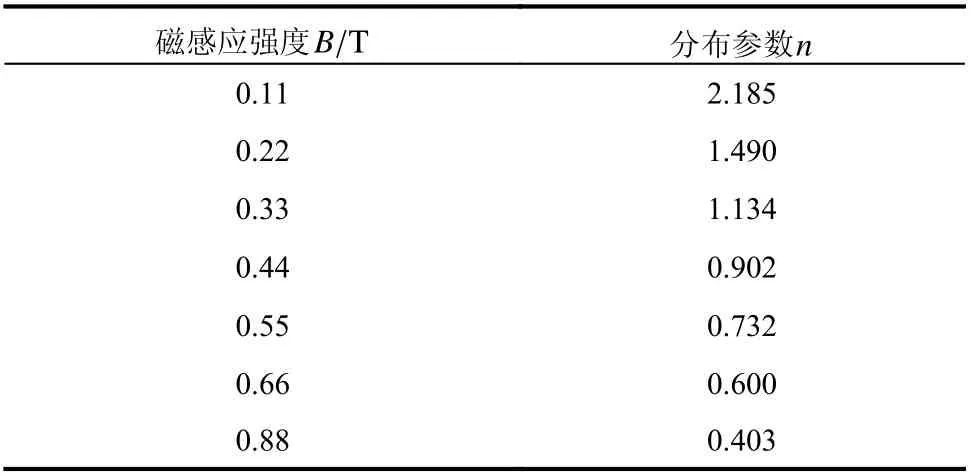
表2 不同磁感應強度下的分布參數Table 2 Distribution parameters with different magnetic induction intensities

利用Origin 軟件中的數據擬合工具，對表2的數據進行參數擬合，可以得到分布參數n隨磁感應強度B的變化關系，擬合曲線如圖2 所示。從圖2 可以看出，分布參數隨磁感應強度的增大而減小，并逐漸趨于穩定。分布參數n隨磁感應強度B變化的公式可表達為：

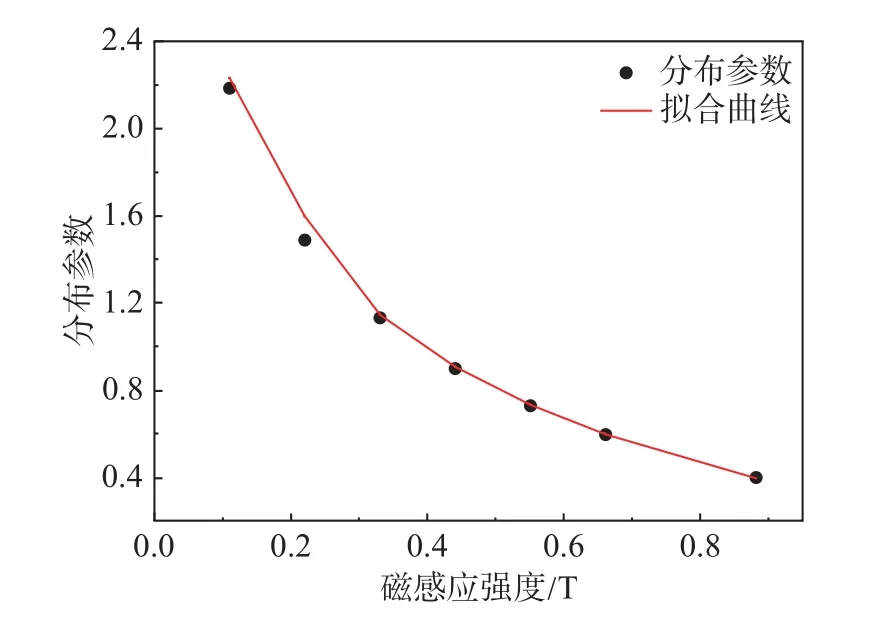
圖2 分布參數隨磁感應強度變化關系的擬合曲線Fig. 2 Fitting curve for variation between distribution parameter and magnetic induction intensity

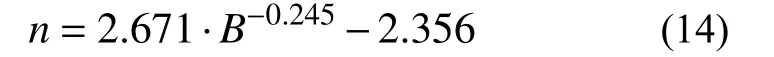
2.2 模型對比

圖3 顯示了磁流變液雙鏈模型、考慮磁性顆粒不均勻分布的修正雙鏈模型的理論計算結果和不同體積分數磁性顆粒下的剪切屈服應力試驗數據的比較。試驗數據采用混合包覆磁流變液剪切屈服應力測試數據[13]，將表1 中數據代入到本文提出的修正雙鏈微觀力學模型和原雙鏈微觀力學模型，可以得到相應的剪切屈服應力理論計算值。試驗數據選取磁性顆粒體積分數為42%和44%工況下的磁流變液剪切屈服應力測試數據。

由圖3 可以看出，當磁感應強度超過0.5 T時，雙鏈模型和修正的雙鏈模型都與試驗數據吻合較好，兩個微觀力學模型的計算結果略低于試驗數據。產生這種現象的原因是當磁感應強度過高時，磁流變液中的磁性顆粒會進一步聚集，形成三鏈狀甚至更為復雜的柱狀微觀結構，這是雙鏈微模型無法準確描述的。當磁感應強度小于0.5 T時，修正的雙鏈模型與試驗數據十分接近，而雙鏈模型的結果則高估了磁流變液的實際剪切屈服應力。相比于原雙鏈模型，改進的雙鏈模型考慮到低磁感應強度下磁性顆粒分布的不均勻性以及顆粒間距隨磁感應強度的變化，即在式(13)的修正雙鏈模型中引入分布函數w(n)來表征磁性顆粒的卡方分布，并通過式(14)引入了磁性顆粒間距隨磁感應強度的變化，從而降低了低磁感應強度下力學模型計算得到的磁流變液剪切屈服應力。試驗數據之間的誤差逐漸減小。當磁感應強度大于0.44 T 時，雙鏈模型和修正雙鏈模型計算結果與試驗數據非常接近，誤差均小于5%。而當磁感應強度小于0.44 T 時，雙鏈模型計算結果與試驗值有較大差距，在磁感應強度為0.11 T 和0.22 T時，誤差分別達到61.43%和48.13%。誤差產生原因是原雙鏈模型假設磁性顆粒均勻分布，顆粒間距為固定值。但實際情況是在低磁感應強度下，磁性顆粒的分布十分的不均勻，均勻分布假設會大大高估低磁感應強度下磁流變液的剪切屈服應力。而修正的雙鏈模型與試驗數據吻合較好，在所有磁感應強度下的誤差均小于15%。因此，通過引入分布參數，磁性顆粒的不均勻分布和顆粒間距隨磁感應強度的變化被考慮到了雙鏈微觀力學模型中，改進的雙鏈微觀力學模型有效地解決了原雙鏈模型高估了低磁感應強度區剪切屈服應力的問題。

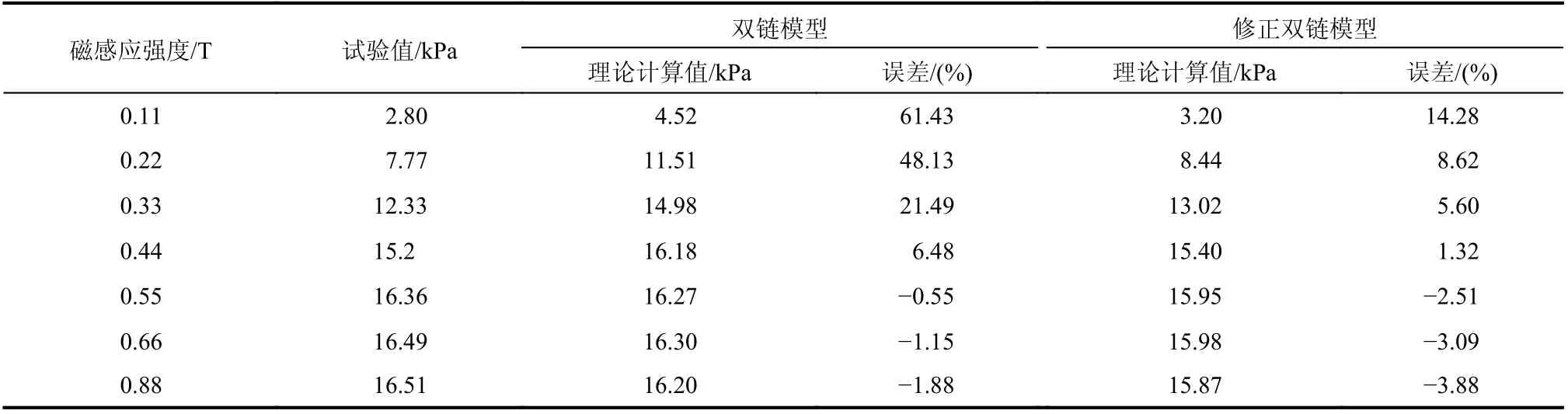
表3 雙鏈模型和修正雙鏈模型理論計算值與試驗值誤差Table 3 Errors between test data and theoretical value calculated by two-column model and modified two-column model

2.3 參數分析

從式(13)的磁流變液修正雙鏈微觀力學模型中可以看到，影響磁流變液剪切屈服應力的主要因素有磁性顆粒半徑、體積分數、包覆層厚度、磁感應強度和本文引入的分布參數。除了分布參數，其余因素對磁流變液剪切屈服應力的影響均被研究討論過[13]，因此，本文著重考察分布參數對磁流變液剪切屈服應力的影響。選取磁性顆粒體積分數為42%，磁感應強度為0.66T，根據式(13)和式(14)的力學模型來計算不同分布參數下剪切屈服應力，如圖4。從圖4 可以看出，當分布參數較小時 (n≤3)，磁流變液的剪切屈服應力隨著分布參數的增大而迅速降低。分布參數表征了磁性顆粒的分布密集程度，圖4 的變化趨勢表明磁性顆粒分布越密集，磁流變液的剪切屈服應力越大，這也符合式(13)的微觀力學模型，剪切屈服應力隨著顆粒間距的減小呈指數級增長。而當分布參數大于7 時，剪切屈服應力逐漸下降為0 并趨于穩定，這表明當磁性顆粒間距過大時，磁鏈逐漸分解，磁流變液的磁致效應基本上消失。因此，為了提高磁流變液的剪切屈服應力，需要盡可能地減小分布參數，即保證磁性顆粒的分布盡量密集。

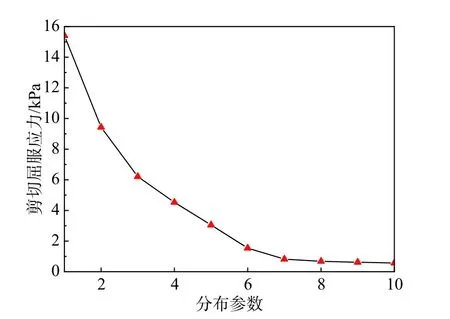
圖4 剪切屈服應力與分布參數的關系曲線Fig. 4 Relationship between yield shear stress and distribution parameter

3 模型試驗驗證

從第2 節對比可以發現，修正的磁流變液雙鏈微觀力學模型可以較為精確地描述不同磁感應強度下的剪切屈服應力。為了進一步驗證考慮磁性顆粒不均勻分布的磁流變液修正微觀力學模型的有效性和準確性，可以將根據修正磁流變液微觀模型計算得到的剪切屈服應力帶入到阻尼器的力學模型中，求得不同電流下磁流變阻尼器的最大出力理論值，并與阻尼器力學性能試驗數據進行對比。

本文將磁流變液修正微觀力學模型代入到經典的偽靜力模型[16-17]中(式(15))，可以求得磁流變阻尼器的最大出力。由式(15)可見，磁流變阻尼器的阻尼力分為庫倫力Fτ和粘滯力Fη兩部分，庫倫力Fτ與磁流變液的剪切屈服應力有關，粘滯力Fη與磁流變液的零場粘度有關[18]。

將磁流變液的參數和單線圈磁流變阻尼器的參數代入式(16)，可以得到磁流變阻尼器的最大出力。為了驗證基于本文提出的磁流變液修正微觀力學模型求得的阻尼器最大出力計算值的準確性，本文對課題組設計制作的單線圈磁流變阻尼器進行力學性能試驗[19-20]，如圖5，并對其力學性能試驗數據進行對比分析。阻尼器內部灌注的磁流變液采用文獻[13]中配制的混合包覆磁流變液，磁流變阻尼器的基本尺寸參數如表4。阻尼器最大出力的實際值可以從磁流變阻尼器的在不同電流下的力-位移滯回曲線中得到，如圖6。相應的激勵頻率為0.1 Hz，位移幅值為5 mm。從圖6中不同電流下的磁流變阻尼器最大出力可以看出，當電流在0 A 增加到1 A 時，阻尼器的最大出力增長迅速，而當電流大于1 A 時，阻尼器的最大出力增幅減緩，呈現出磁飽和的現象。因此，磁流變阻尼器的出力可調性更多地體現在低電流工況下，0 A～1 A 是實際應用中磁流變阻尼器常用的工作范圍[21]。本文提出的磁流變液修正力學模型在低電流情況下精確度更高，具有實際工程意義。

圖5 單線圈磁流變阻尼器力學性能試驗Fig. 5 Performance tests of single-coil MR damper

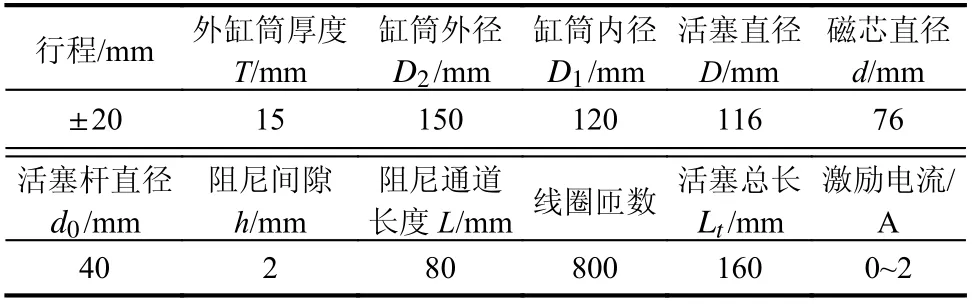
表4 磁流變阻尼器基本尺寸參數Table 4 Basic dimension parameters of MR damper

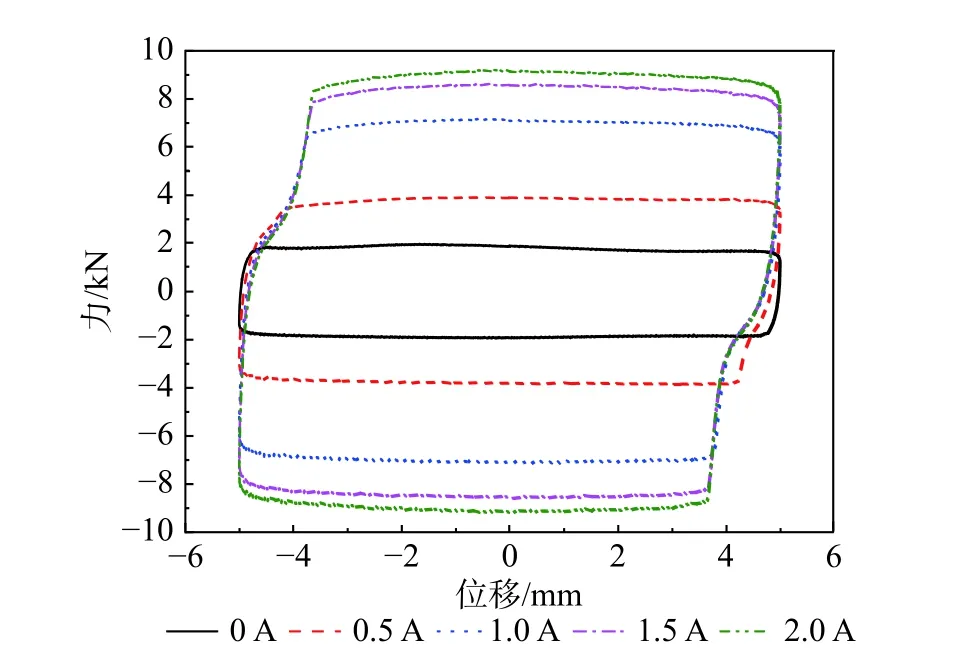
圖6 磁流變阻尼器力-位移滯回曲線Fig. 6 Force-displacement hysteretic curves of MR damper

圖7 顯示了由修正的雙鏈微觀力學模型計算得到的最大阻尼力理論值與由圖6 得到的磁流變阻尼器性能測試結果的比較。如圖7 所示，基于磁性顆粒卡方分布的修正雙鏈微觀力學模型計算得到的最大阻尼力與性能試驗結果吻合良好。當激勵電流為0 A、0.5 A、1.0 A、1.5 A、2.0 A 時，阻尼器力學性能試驗測得的最大阻尼力分別為1.96 kN、3.90 kN、7.17 kN、8.62 kN、9.21 kN。修正的雙鏈微觀力學模型計算結果分別為2.05 kN、4.04 kN、7.05 kN、8.52 kN、8.93 kN，誤差分別為4.59%、3.59%、3.35%、4.76%、3.04%，誤差均控制在5%以內。而基于磁性顆粒均勻分布假設的雙鏈微觀力學模型計算得到的理論值分別為2.57 kN、4.28 kN、7.25 kN、8.82 kN、8.95 kN，誤差分別為31.12%、9.74%、1.12%、0.58%、2.82%。從原雙鏈模型計算結果的誤差可以發現，在低電流情況下模型誤差較大，隨著電流的增大，誤差逐漸恢復到可接受的范圍內，這也與第2 節磁流變液剪切屈服應力的對比結果一致。比較修正雙鏈模型和原模型的計算誤差可以發現，相比于原雙鏈模型，根據磁流變液的修正雙鏈模型計算得到的阻尼器最大出力在低電流下(<1.0 A)更加符合試驗數據，即可以更加準確地描述剪切屈服應力與磁感應強度之間的關系。將本文提出的磁流變液修正雙鏈微觀力學模型與磁流變阻尼器準靜態模型相結合，可以準確估算磁流變阻尼器的最大出力，適合用于磁流變阻尼器的尺寸設計。

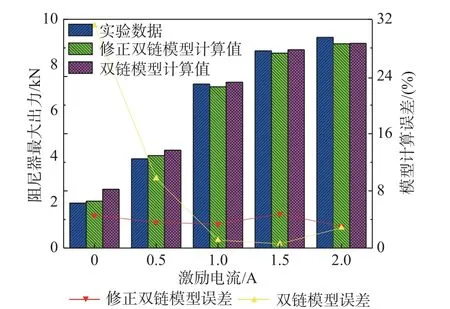
圖7 磁流變阻尼器最大出力理論計算值和試驗值對比Fig. 7 Comparison between theoretical and experimental results of maximum output of MR damper

另外，從圖6 可以發現磁流變阻尼器存在明顯的磁飽和特性，該單線圈磁流變阻尼器飽和電流約為1.5 A。而從圖3 可以看出，磁流變阻尼器的磁飽和特性可歸因于磁流變液的剪切屈服應力與磁感應強度之間的非線性關系。隨著激勵電流的增大，磁流變液的剪切屈服應力先增大后趨于穩定，最終導致磁流變阻尼器的出力呈現出明顯的磁飽和現象。因此，利用本文提出的修正磁流變液微觀力學模型來推導磁流變阻尼器的力學模型，可以將阻尼器的磁飽和特性考慮進去。

4 結論

本文用卡方分布來描述磁性顆粒在磁場作用下的不均勻分布，提出了修正的磁流變液雙鏈微觀力學模型，并通過磁流變阻尼器的力學性能試驗驗證了該模型的準確性，得到如下結論：

(1)在磁流變液雙鏈微觀力學模型中引入分布參數來表征磁性顆粒的分布密集程度及顆粒間距隨磁感應強度的變化，彌補現有微觀力學模型中磁性顆粒均勻分布假設的不足，提出了考慮磁性顆粒卡方分布的磁流變液微觀力學模型。模型形式簡單，可以反映磁性顆粒不均勻分布、鄰鏈影響、磁飽和特性以及磁流變液多個微觀結構參數對剪切屈服應力的影響。

(2)對比磁流變液性能試驗數據可以發現，修正后的力學模型可以準確預測磁流變液在不同磁感應強度下的剪切屈服應力，特別是在低磁感應強度情況下可以改善現有微觀力學模型放大了磁流變液剪切屈服應力的缺點。

(3)磁流變液的剪切屈服應力會隨著分布參數的增大而減小。當分布參數較小時，剪切屈服應力隨著分布參數的增大而迅速降低。而當分布參數大于7 時，磁流變液的剪切屈服應力逐漸下降為0 并趨于穩定，表明此時磁性顆粒間距過大，磁鏈逐漸分解，磁致效應基本上消失。

(4)將本文提出的磁流變液修正微觀力學模型代入阻尼器準靜態模型中，可以計算阻尼器的最大出力。對比不同電流下的最大出力理論計算值和單線圈磁流變阻尼器性能試驗數據，進一步驗證了該磁流變液修正模型的有效性和準確性。該方法可以準確估算磁流變阻尼器的最大出力，適合用于磁流變阻尼器的尺寸設計。