基于ABAQUS基礎面外附加壓應力數值模擬及簡化方法研究

汪學智，王超群，吳 桐，田佳甲

(陜西中海建工程設計院有限公司，陜西 西安 710075)

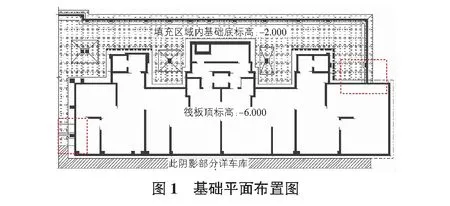
隨著經濟及科技的日益發展，人們對環境及建筑功能要求日益提高，越來越多的復雜建筑應運而生，復雜不僅僅體現在外立面及使用功能上，建筑地下基礎的布置方案及受力形式也越來越復雜，由此帶來的困擾也越來越多。例如現行規范《建筑邊坡工程技術規范》對于擋土墻附加側向土壓力的計算方法雖有明確規定，但從中所列種類可看出，其荷載布置方向均不包括垂直擋土墻方向，而在實際工程中該類情況也較為常見，尤其當主樓連帶商業、商業無地下室且商業條形基礎與主樓基礎存在高差時更為常見，如圖1所示。

與擋土墻垂直的條形基礎的分布荷載，對擋土墻的作用力相較之于平行方向時較小，但仍不可忽略[1-2]，工程中普遍的做法就是對該擋土墻進行適當加強，但如何加強，加強多少卻比較模糊。鑒于此，本文結合實際工程，采用有限元分析軟件ABAQUS對其進行數值模擬，以期得出較為貼合實際的結果，并以此為相關工程提供參考。

1 工程概況

某工程位于陜西省西安市，建筑使用年限50 a，抗震設防烈度8度，地基基礎設計等級乙級。主樓為26層剪力墻結構，附帶3層商業，主樓含1層地下室，商業不含地下室，根據結構布置及基礎形式，主樓為筏板基礎，商業基礎為墻下條形基礎，如圖1所示。圖1中虛線框中部位基礎存在較大高差，使主樓擋墻平面外相接條形基礎。本文則著重研究該條形基礎對主樓擋土墻的平面外影響。

2 基于ABAQUS有限元數值模擬

2.1 模型參數選取

土體應力應變關系是十分復雜的，通常具有非線性、彈塑性、剪脹性和各向異性等特點，迄今為止，學者們所提出的土體模型都只能模擬某種加載條件下某類土體的主要特征[3-4]。實踐證明，Mohr-Coulomb模型的參數不僅容易確定，而且其在以極限承載力為分析重點的問題中非常合適[5-7]。其塑性模型主要適用于單調載荷下顆粒狀材料，適用于巖土工程中。因此，本文土體數值模擬采用該模型。

Mohr-Coulomb模型屈服面函數為：

F=Rmcq-ptanφ-c=0。

其中，φ為q-p應力面上Mohr-Coulomb屈服面的傾斜角，即摩擦角；c為材料黏聚力；Rmc(Θ，φ)按下式計算，其控制屈服面在π平面的形狀。

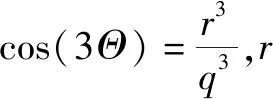
Mohr-Coulomb模型勢面函數為：

其中，ψ為剪脹角；cl0為初始黏聚力；ε為子午面上的偏心率。

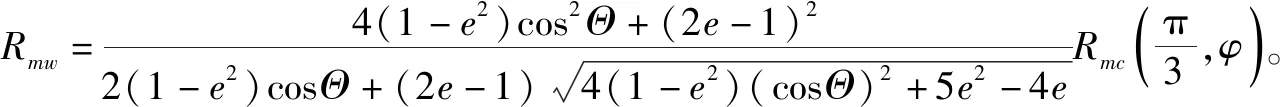
土體材料本構參數采用地勘資料提供數據，本文為了研究目的的明確性，對擋土墻高范圍土質材料采用均質理想彈塑性材料，以減少多余變量的干擾，土體彈性模量取值207 MPa，泊松比取值0.3，土體擴散角取值20°，材料塑性參數列于表1。

表1 Mohr-Coulomb塑性本構參數

基礎及擋墻混凝土采用C30，屈服抗壓強度取值14.3 N/mm2，彈性模量30 000 N/mm2。

本文采用3D可變形實體拉伸單元模擬擋土墻、條形基礎及土體，并定義擋墻與土體間摩擦系數0.2，以模擬二者間的有限滑動，基礎底面與土體間完全綁定，擋墻頂部限制X向與Z向位移，以模擬頂部結構板對擋墻側移的約束，并在Load中不加載重力，由此得出的側向壓應力即為基礎產生的附加側向壓應力[8]。建立ABAQUS有限元分析模型，如圖2所示。為了分析研究其在特殊工況下附加側向土壓力的大小及分布規律，本文兼顧實際工程常見的基礎寬度及基底壓應力的范圍取值，以基礎基底壓應力大小和基礎寬度為變量，工況變量列于表2。

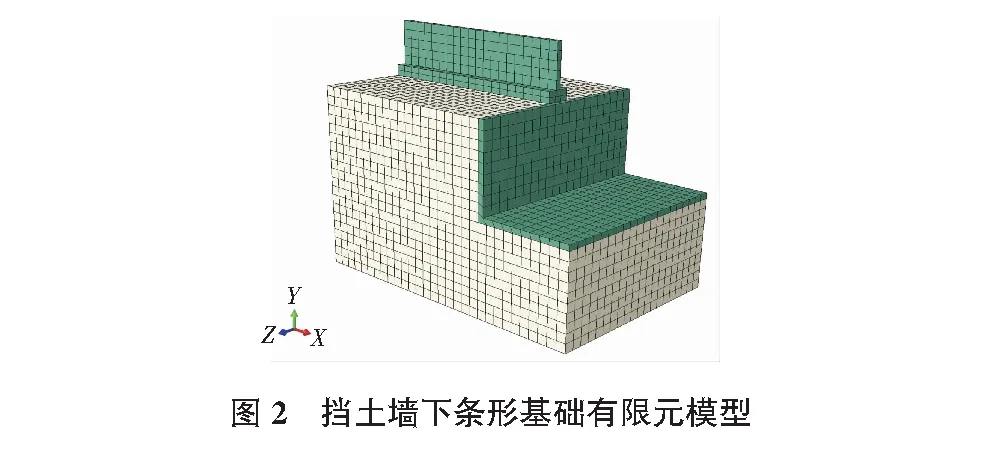
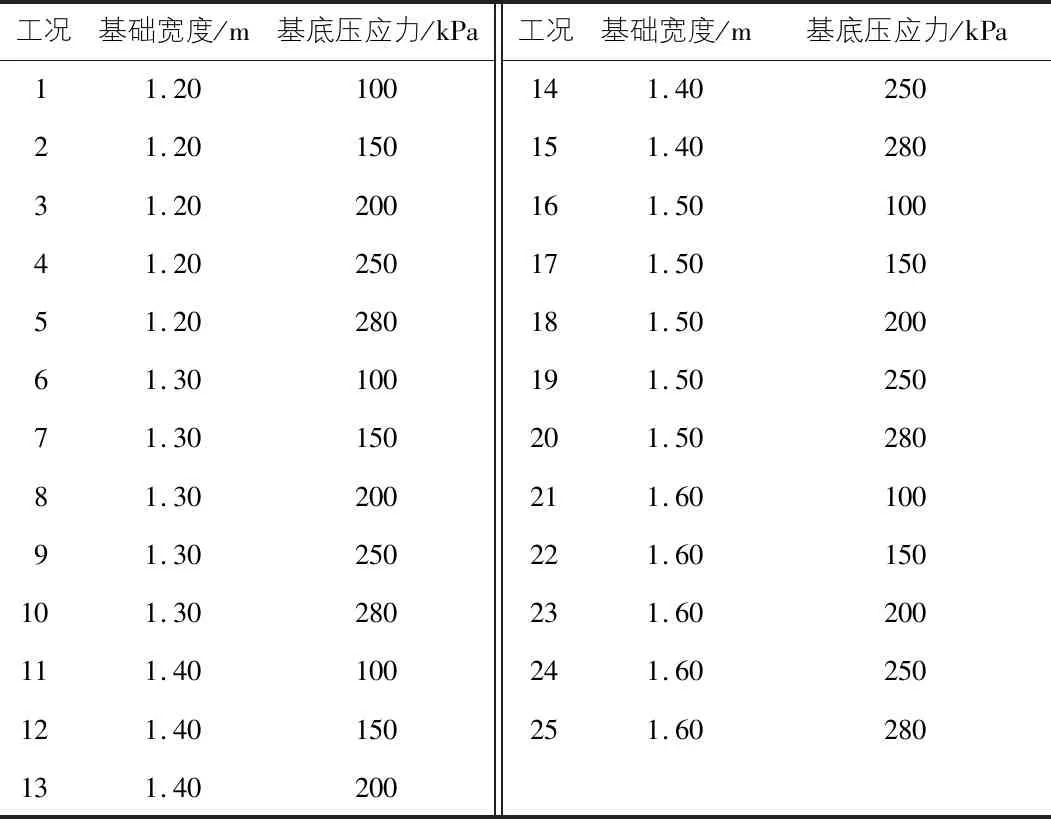
表2 擋土墻工況表

2.2 數值模擬分析

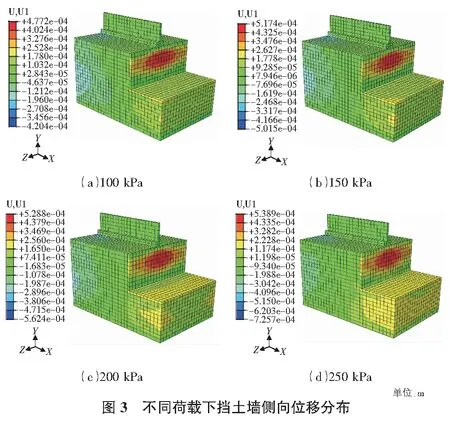
以1.20 m寬擋土墻基礎在100 kPa～280 kPa工況為例，經有限元分析，得出不同工況參數下擋土墻的側向位移，如圖3所示。由圖3可知，側向位移分布呈如下規律：由于擋墻頂部結構板的側移限值，位移隨土層深度的增加先增大后減小，隨距擋土墻基礎水平距離的增加而減小，并且在整體受力范圍內，位移均非常小，在最大基底壓應力280 kPa的工況下，擋土墻最大側向位移僅為0.54 mm，即工程中當條形基礎基底壓應力不超過280 kPa時，可以忽略由此產生的側向位移。

擋土墻側向壓應力分布如圖4所示。由圖4可知，附加側向壓應力的大小隨著深度的增加而減小，隨著距擋土墻基礎水平距離的增加而急劇減小，水平分布范圍基本均在基礎寬度范圍內。不同工況下擋土墻附加側向壓應力匯總于表3。

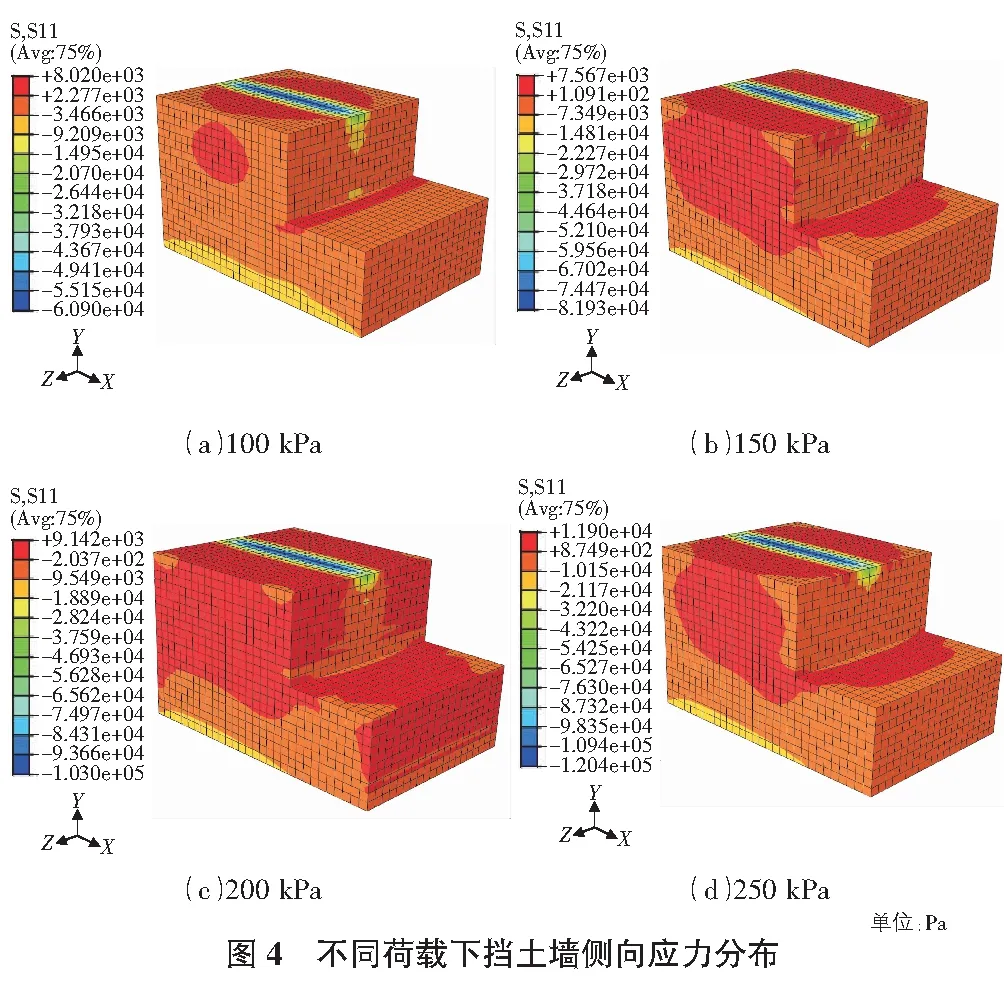
表3中占比指擋土墻最大附加壓應力與基底壓應力的比值百分數。由表3可知：當基礎寬度不變時，基底壓應力越大，擋墻受到基礎傳來的附加側向壓應力也越大；當基底壓應力不變時，基礎寬度越大，擋墻受到基礎傳來的附加側向壓應力越小，最大附加側向壓應力占比也越小。

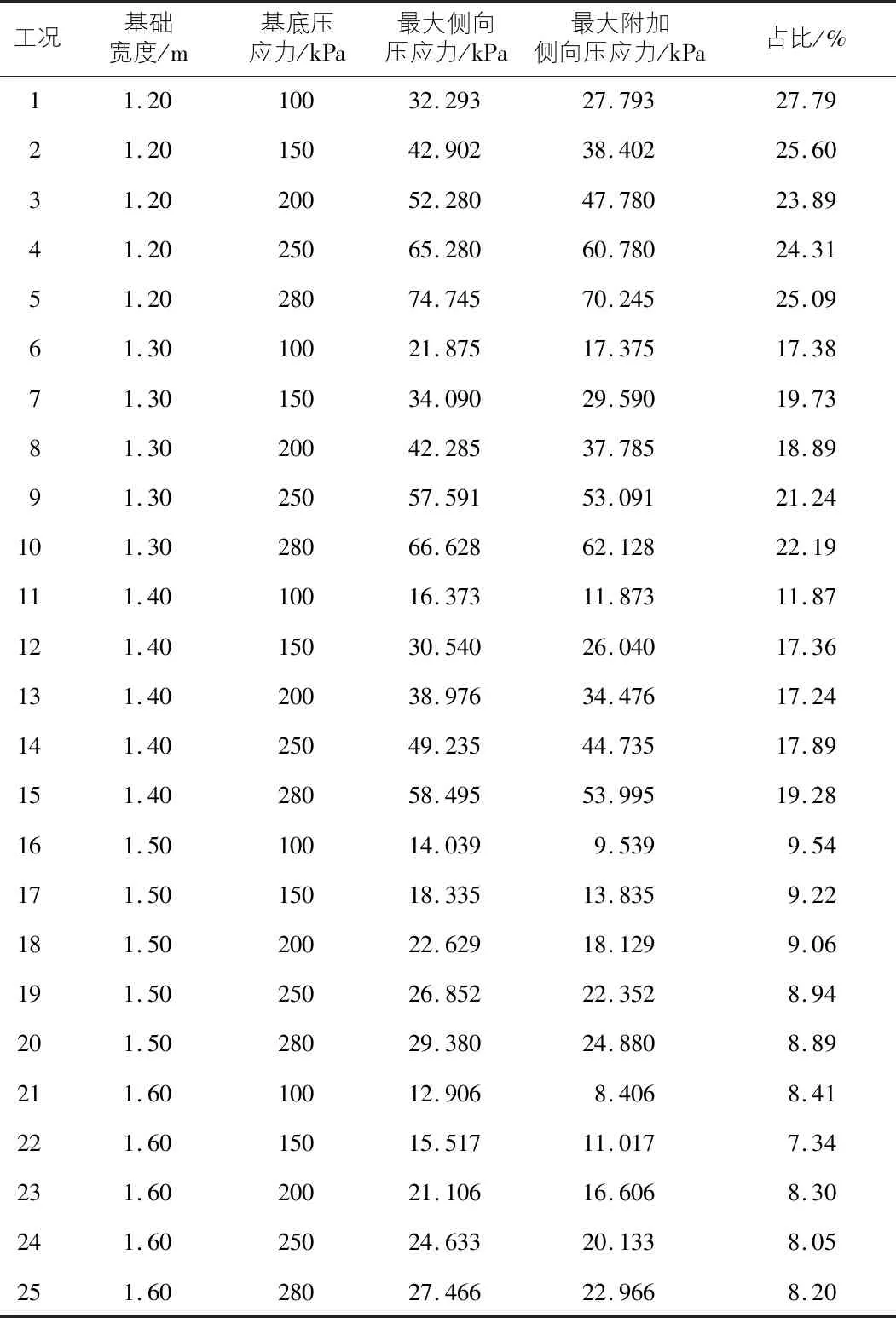
表3 擋土墻附加側向壓應力

3 工程簡化方法應用研究

為了使實際工程應用較為簡便實用，根據有限元模擬數據結果，曲線以一次線性曲線擬合，擬合如圖5所示。由圖5可知，基礎寬度在1.20 m～1.40 m之間時，曲線斜率最大為0.244 3，基礎寬度大于1.50 m時，曲線斜率最大為0.085 2。即當基礎寬度不大于1.40 m時，擋土墻附加側向壓應力隨基底壓應力的增加有較為顯著的增大，而當基礎寬度不小于1.50 m時，擋土墻附加側向壓應力隨基底壓應力的增加僅有緩慢的增幅，增幅不顯著。

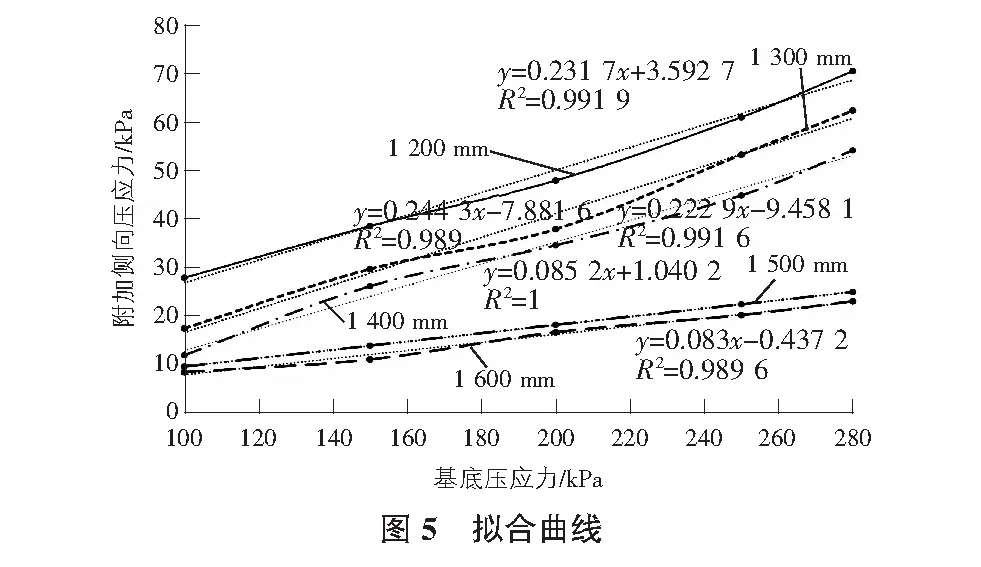
結合文獻[9-10]的研究成果，兼顧土體摩擦角、擴散角及基礎寬度的變量，保證結構安全性及經濟性的前提下，現對擬合方程進行簡化，則有：

(基礎寬度B≤1.4 m)。

(基礎寬度B≥1.5 m)。

其中，x為基礎基底壓應力，kPa；y為擋土墻附加側向壓應力，kPa；B為基礎寬度，m；c為摩擦角；φ為擴散角；K為系數，靜止土壓力時為0.5，主動土壓力時為0.4，被動土壓力時為0.6。

4 簡化方法的驗證

為了驗證本文擬合簡化公式的實用性，現對該公式進行數值模擬驗證，驗證項次如表4所示，其中土質參數及結構布置均按前述。

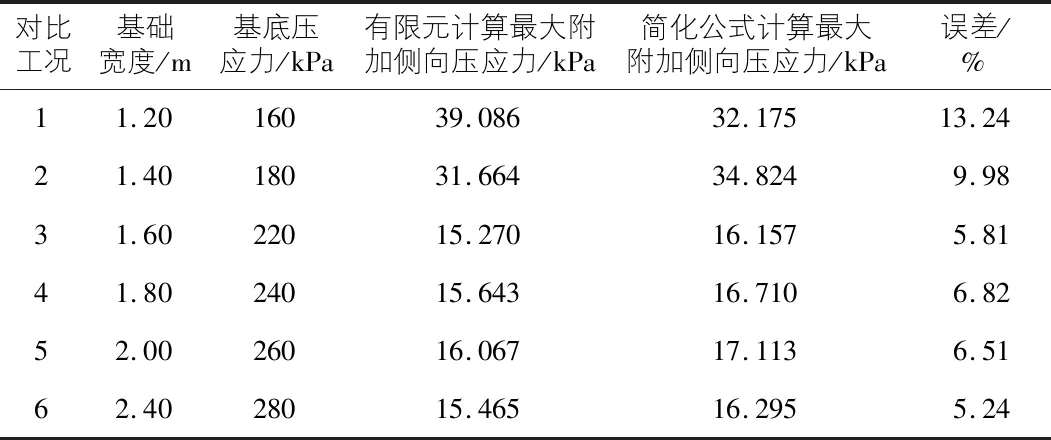
表4 公式驗證

由表4可知，簡化公式計算結果與有限元數值模擬結果較為接近。由于基礎寬度1.4 m以內有限元數值模擬曲線較為分散，為了保證工程安全，簡化公式取為曲線包絡值，導致誤差較大；基礎寬度1.5 m以上時，曲線較為聚攏，簡化公式能夠較好的反映數值分析結構，并且隨著基礎寬度的增大，二者誤差越來越小。因此，該簡化公式可較好的反映有限元數值模擬的結果，能夠較為安全、經濟的適用于實際工程中。

5 結論

本文通過對實際工程中擋土墻的數值模擬，結合理論分析，總結歸納出適用于實際工程中的擋土墻附加側向土壓力的簡化計算方法，并通過有限元復核驗證了該方法的實用性及有效性，得到如下主要結論：

1)對同一條形基礎，隨著基底壓應力的增大，擋土墻附加側向壓應力也隨之增大，增大幅度隨基礎寬度的增加而減小。

2)基礎寬度1.40 m以內時，擋土墻附加側向壓應力的大小隨基礎寬度的變化趨勢較為離散，而當基礎寬度大于1.50 m時，該變化趨勢趨于穩定。

3)本文簡化公式在基礎寬度大于1.5 m時，簡化公式與有限元分析結果之間誤差較小，能夠較好的體現有限元數值分析結果，能夠較為安全、經濟的應用于實際工程中。