風電場經VSC-MTDC并網的交直流系統最優潮流計算

黃榮澤

(百色新鋁電力有限公司調度中心，廣西 百色 533000)

0 引 言

由多個直流換流站經過串聯、并聯或混聯連接成的直流輸電系統稱為多端柔性直流輸電(voltage source converter based multi-terminal direct current system，VSC-MTDC)，VSC-MTDC相比于兩端直流輸電系統能夠更好地協調各個換流站之間的潮流分配，靈活性和可靠性更好，適用于可再生能源并網、向大負荷中心供電及異步交流系統聯網等場景[1-3]。

潮流計算是電力系統規劃和運行的基礎，因此研究包含VSC-MTDC的交直流輸電系統的潮流計算具有重要的意義。該文根據VSC-MTDC的工作原理，建立適用于內點法最優潮流計算(optimal power flow，OPF)的穩態模型，并將公共直流結點加入到模型中，應用場景分析法模擬風電場出力的概率分布，并應用預測-校正內點法對模型進行求解。

1 VSC-MTDC交直流輸電系統穩態模型

1.1 單個VSC換流站模型

單端VSC換流站與交流電網連接的等效電路圖如圖1所示[4]。

圖1 VSC-HVDC 模型Fig.1 Model of VSC-HVDC

圖中Us，i∠θs，i為交流系統的電壓，Uc，i∠θc，i為VSC換流站的輸入電壓，XL,i為換流變壓器的電抗，Ri為換流變壓器損耗的等效電阻，Ps，i、Qs，i分別是交流系統和直流系統交換的有功功率和無功功率，Pc，i、Qc，i分別是從換流變壓器進入換流器的有功功率和無功功率，Ud，i、Id，i分別是換流器輸出的直流電壓和直流電流。根據PWM調制原理，換流站輸出的直流電壓與輸入的交流電壓關系為

(1)

式中：Uc，i為換流站輸入電壓Uc，i∠θc，i的有效值，Mi為PWM的調制度(0≤M≤1)，即正弦調制峰值與三角載波幅值的比值。

根據圖1所示的示意圖，可推導出其穩態潮流方程如下：

(2)

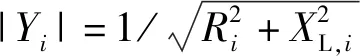
1.2 VSC-MTDC并網的交直流系統模型

如何將VSC的穩態模型和交流系統潮流方程結合起來進行求解，是解決含VSC的交直流系統最優潮流計算的難點。為了方便討論，將連有VSC的節點稱為直流節點，其他節點稱為交流節點[5-6]。

對于交流節點，可列出潮流方程如下：

(3)

式中：ΔPs，i、ΔPs,i表示交流節點有功不平衡量和無功不平衡量;Ps，i、Qs，i為交流節點發出的有功功率和無功功率;Ui表示節點電壓;Gij、Bij表示相連2個節點之間的電導和電納;θij表示相連2個節點之間的電壓相角差。

對于直流節點，在原來交流節點上增加了直流變量，根據圖2所示系統，可列出其潮流方程如下：

圖2 修改后的11節點交直流系統Fig.2 Modified IEEE-11bus of AC-DC system

(4)

式中：ΔPt,i、ΔQt,i表示直流節點有功不平衡量和無功不平衡量;Pt,i，Qt,i為VSC從交流母線吸收的有功和無功功率；Ut,i為連有VSC的交流母線的電壓幅值。

以2區4機系統為例[7]，風電場經三端VSC并網。直流公共連接點(direct current point of commoncoupling，DC-PCC)的電壓也是未知量，需要在計算中求得，DC-PCC的潮流方程為

(5)

式中：ΔI表示DC-PCC節點電流不平衡量;Udc，j為DC-PCC點電壓;Gdc，j為與DC-PCC點連接支路的電導;Nd為直流線路的支路數。

1.3 風電場出力模型

風電場和火電、水電等傳統電源不同，其出力存在較大的波動性，所以在對含風電場的電網進行優化時必須考慮其波動性，否則可能導致傳統的調頻電源無法快速調整出力，造成系統頻率劇烈波動，威脅電網安全。

通常應用場景分析法來模擬風電場出力的波動性。場景分析法通過幾個容易確定的場景來描述復雜多變的隨機事物，以減小計算復雜度。為了減少計算耗時，采用場景分析法來模擬風電場出力的波動性，將風電場某一段時間出力的預測值稱為預測場景，預測所產生的誤差稱為誤差場景。通常風電場的短期出力服從正態分布[8]：所以誤差場景可由式(6)給出：

(6)

式中：Pd為誤差場景出力值;μ為風電場出力預測值；σ為預測值的標準差。通常風電場出力預測的誤差為25%～40%，假設出力預測誤差為30%，即σ2=30%。

當風電出力波動時，為了保證系統頻率在正常值范圍內，需要網內的火電機組或水電機組能夠快速地調整出力，保證系統發供電處于平衡狀態。對于圖1的系統，假設4個火電廠快速調整出力的范圍是其額定功率的±8%，如式(7)所示：

(7)

2 含 VSC-MTDC 的交直流系統內點法OPF

含VSC-MTDC的交直流系統的OPF模型[9-10]可表示為

(8)

應用內點法求解含不等式約束的優化模型基本思路是通過引入松弛變量將模型中的不等式約束轉化為等式約束，并利用障礙函數對松弛變量進行約束，再把目標函數改造為障礙函數，這樣便把含不等式約束的優化問題變成只含等式約束的優化問題，最后用拉格朗日乘子法求解。

將式(8)構造的拉格朗日函數,如式(9)所示：

(9)

式中：y=[y1,…,ym]，z=[z1,…,zr]，w=[w1,…,wr]為拉格朗日乘子;l=[l1,…,lr]T，u=[u1,…,ur]T為松弛變量；μ為障礙常數。該模型的最優解存在的必要條件為拉格朗日函數對所有變量及乘子的偏導為0，如式(10)所示：

式中：L=diag(ll,…,lr)，u=diag(ul,…,ur)，Z=diag(zl,…,zr)，w=diag(wl,…,wr)，e=[1,…,1]T。

由式(10)最后的2個方程可以求出μ=(lTz-uTw)/(2r)，定義Gap=lTz-uTw為對偶間隙，Fiacco和McCormic證明在一定的條件下，迭代過程中當Gap趨于0時，變量x將收斂于目標函數最優值[10]x*，所以內點法迭代過程中收斂的條件為Gap接近于0，通常當Gap小于10-6時即可認為變量x值為目標函數的最優解。通常目標函數中的罰因子μ按照式(10)取值時迭代過程收斂較差，一般采用μ=σGap/(2r)，式中σ稱為中心參數，一般取0.1時迭代過程具有良好的收斂性。

通過采用牛頓法對非線性方程組式(10)進行求解，即可求得含VSC-MTDC的交直流系統最優潮流模型的最優解。將其線性化可得

(11)

(12)

(13)

求解方程(11)～(13)即可得到第k次的迭代修正量Δx,Δy,Δz,Δl,Δu,Δw。

式(12)中的中心參數σ是影響迭代收斂性的重要參數，預測-校正內點法的實質是對中心參數σ的動態預測，在每一次迭代過程中通過預測步求出仿射方向修正量以修正μ增加一次前代回代計算，然后利用估計互補方程求出校正修正量。具體步驟如下：

1)預測步：

① 設定中心參數σ=0。

② 求解式(11)～(13)，得到仿射方向Δxaff,Δyaff,Δzaff,Δlaff,Δuaff,Δwaff。

(14)

(15)

(16)

⑤ 動態估計中心參數：

(17)

2)校正步：

①對互補松弛條件進行修正:

(18)

(19)

3 算例分析

以圖2所示的4機11節點系統為例，利用Visual Basic 6.0編程計算，驗證所討論模型的有效性。其中，風電場經3端VSC并入系統的5、7節點。假設風電場有功出力為5 (p.u.)(系統容量基準值為100 MVA)。直流線路參數見表1，各個發電機發電費用見表2。

表1 直流系統參數Table 1 Parameters of DC system

表2 各火電廠發電成本函數Table 2 Power generation cost function of each thermal power plant

表1中：R表示換流器有功損耗的等效電阻，XL為換流變壓器電抗，R12，14、R5，14、R7，14為直流線路電阻，Xt為12、13節點間風電場升壓變壓器的電抗。同時，假定系統內所有的換流站參數相同。表2中發電機發電成本函數表示當發電機有功出力為P(取標幺值，無單位)時，運行1 h的成本。

3.1 算法效率比較

圖3為不考慮誤差場景條件下分別采用該文所提預測-校正內點法和原對偶內點法對VSC-MTDC最優潮流計算模型進行優化時迭代次數的比較(圖中為了便于觀察只畫出迭代過程接近收斂部分)。從圖3可以看出：在相同條件下，2種優化算法的收斂曲線變化趨勢一致，迭代過程中補償間隙一直是下降的，在有限次迭代步內都能收斂到給定精度；采用該文所提的預測-校正內點法比原對偶內點法少迭代60次，效率有較大提升。

圖3 收斂特性比較Fig.3 Comparison of convergence characteristics

3.2 多個誤差場景計算結果比較

為了節省計算時間，分別取2組5個誤差場景和 2 組10個誤差場景的風電場4組出力數據模型進行計算(見表3)，討論誤差場景標準差和場景數量對所提算法的影響。計算結果如圖4(圖中為了便于觀察只畫出迭代過程接近收斂部分)、表4和表5所示。表4中PG1、PG2、PG3、PG4表示圖2中1～4號發電機有功出力值，表5中M5、M7、M12表示圖2的交直流系統中節點5、7、12的換流器的調制度，δ5、δ7、δ12表示節點5、7、12的換流變壓器的輸入端和輸出端的相位差。從圖4可以看出:在相同的誤差場景數量條件下，誤差場景標準差越大,需要的迭代步驟越多，表明當風電場出力波動較大時，需要更多的迭代步驟才能得到最優結果；當誤差場景標準差相近時場景數增加后優化過程迭代次數明顯增加，這是由于引入更多的誤差場景之后約束條件增加，需要更多的迭代步驟才能獲得最優解。從表4可以看出:誤差場景標準差(即風電出力波動性)對系統總的發電成本影響較小，但當誤差場景增多后發電成本上升，這是由于引入更多的誤差場景后約束條件變多，使得模型可行域變小，所有優化后的發電成本增加。誤差場景個數在優化過程中只影響可行域的大小，進而影響交流控制量的優化結果，直流控制量只受風電場預測值場景的出力大小影響，所以5個誤差場景和10個誤差場景優化后的直流控制量結果相同。表5僅列出了5個誤差場景優化后的直流控制量值。

表3 風電場出力誤差場景及標準差Table 3 Standard deviation of wind farm output error scenarios

表4 計算結果(交流控制量)Table 4 Results of OPF (AC variables)

表5 計算結果(直流控制量)Table 5 Results of OPF (DC variables)

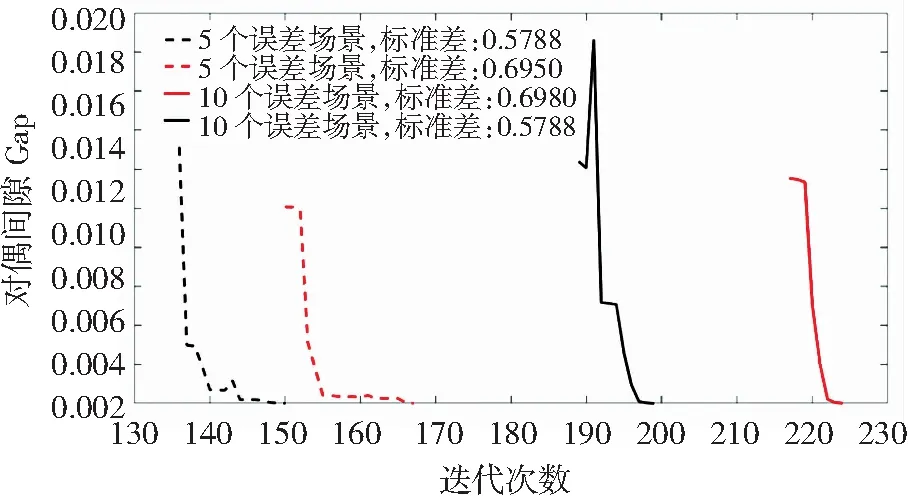
圖4 不同條件下算法收斂特性比較Fig.4 Comparison of algorithm convergence characteristics under different conditions

該文所采用的優化方法為預測-校正內點法，在預測階段，變量x的預測值是通過前一次迭代獲得的x值加上一定的步長獲得，所以獲得的預測值有可能比前一次迭代獲得的值遠離最優解，導致Gap反而增大，但是在目標函數的罰函數的作用下，下一個預測值將快速收斂于目標函數最優解，即Gap將快速趨近于0。所以10個誤差場景，標準差為0.578 8時收斂曲線有上升趨勢后迅速下降，屬于正常的震蕩現象。

4 結 語

根據VSC的穩態模型，建立了風電場經多端VSC并網的最優潮流計算模型，利用場景分析法模擬風電場出力的波動性，以系統總的發電成本最小為目標函數，采用預測-校正內點法對模型進行求解，結果表明：

1)利用預測-校正內點法求解含多端VSC的交直流系統比原對偶內點法具有更好的收斂速度。

2)隨著誤差場景的增加，優化過程中迭代次數也增加，并且系統的發電成本也增加；相同數量的誤差場景條件下，誤差場景標準差越大(即風電出力波動越大)，優化過程中迭代次數也增加，系統的發電成本也增加。