利用變式教學，提高核心素養
——以“數列的通項公式的求法”為例

王 峰

(泗縣第三中學 安徽宿州 234300)

數學核心素養包括數學抽象思維、邏輯推理、數學建模、數學運算、直觀想象與數據分析等方面，它們既相互獨立，又相融相生、相輔相成。在國家“雙減”政策的指引下，如何利用課堂教學，在教學目標中落實核心素養，這是我們教學工作者當前要思考的課題。

變式教學是激活學生的發散思維能力、遷移能力及思維的靈活性的重要方式，是培養學生的數學核心素養的有效方式。利用變式教學，可從多角度和各個層次進行有針對性的設計，引導學生從“變”的現象發現“不變”的本質，從而使學生擁有其未來發展所需要的及必要的邏輯思維能力和解決問題的能力，提高課堂教學效果及學生的數學核心素養。下面我就“數列的通項公式的求法”的案例教學，談談我的一些做法。

一、案例展示

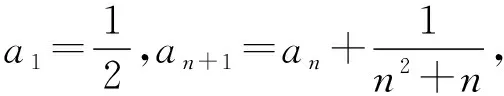
引導 1+1-等于什么?

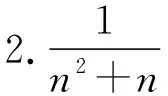
3(-)+(-)+(-)等于什么?

4-等于什么?

設計目的：通過這幾個循序漸進的問題，逐步打開學生解決此題的思路，既符合學生思維發展過程，又促進了學生學習的邏輯思維的提高及數學素養的養成。

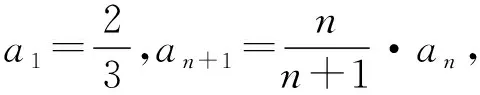
設計目的：通過類比案例一，歸納、推理得出解決此題的方法，讓學生學會觸類旁通，在解決問題的過程中理解知識，促進學生對知識的縱向遷移，從而弄清知識的本質和規律，形成精細化的認知結構。

案例三 已知數列{}中，=3，+1=3-4，求。

引導 1利用前面學習的觀察法、公式法，利用與的關系法、累加法、累商法能否求出此題？

2若有+1-5=3(-5)，可知什么信息？

3對于+1=3-4能構造成第2題這種形式嗎？

4對于+1=+，其中、均為常數，(-1)≠0，求。此類問題如何轉化解答？

設計目的：這里設置的幾個問題，使題目的難度由淺入深、層層遞進，從思想角度給學生以指引，提升學生的數學核心素養。

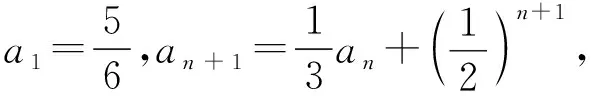
引導 投影一學生的解答過程：

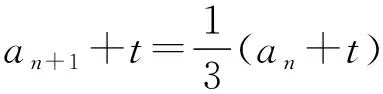
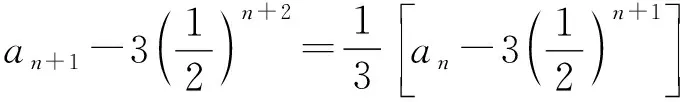
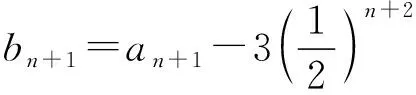
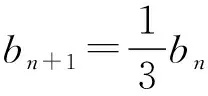
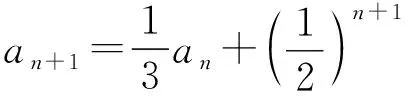
3本題還可以用什么方法解答？投影解答過程(略)

4若一個數列的遞推公式為+1=+(，，-1是均不為0的常數)，如何求？

設計目的:通過幾個問題，幫助學生逐步尋求解題方法，讓學生學會靈活運用所學知識解決問題，挖掘并強化學生的思維深度，讓學生更好地去分析并解決問題，促進他們的邏輯思維等方面數學素養的發展。

案例五 設數列{}滿足=4，=3-1+2-1(≥2)，求

引導 1將=3-1+2-1兩邊同除以(2-1)，行嗎？

2將=3-1+2-1設為+=3(-1+)，可以解出嗎？

3將=3-1+2-1設為++=3[-1+(-1)+]是否行?若行，如何求出、值？

4對于+1=++(≠1，≠0，≠0)，如何求解？

5對于+1=+++(≠1，≠0，≠0)，如何求解？

設計目的：通過這五個由易到難的問題，逐步深入，利用轉化和歸納數學思想方法，使得知識生成自然流暢，符合學生的認知規律，從而優化學生的思維模式，有利于培養學生的理性思維素養。

二、教學反思

在核心素養理念下，學生的學習能力并不是過去所說的應試的能力，而是指學習知識的能力，將所學知識在實踐中創造性運用的能力等，變式教學方式可以有效促使學生獲得這種能力。核心素養的養成來源于數學知識技能又高于它，它是在數學學習的過程中一點一滴逐步形成的。這五個教學案例，通過轉化、類比、歸納等一系列過程，讓學生學習數學的思想方法，積累一定的數學學習活動方面的經驗，進而促進學生的數學核心素養的提高。

課堂上，教師要根據學生的思維能力及教學內容，設計一系列由易到難相關的問題。在向學生發問后，我們給學生一定的時間去思考，學生有了自己的見解后再表達自己的解題思路和方法，這時教師再帶領學生總結、提煉、概括，幫助學生透過問題的表象去看清本質。教師設計的問題要由淺入深有變化，能引起學生的興趣，讓學生積極地投入進去，鼓勵學生討論探究，最終實現提高學生的解題能力這一目標。變式教學方式注重培養學生去發現存在問題，勇于去提出自己的見解并通過實踐行動去分析與解決問題。變式教學方式鼓勵學生帶著問題去思考，注重對學生思維能力的訓練，培養學生用創新的方式解決問題的能力。

在課堂教學中，教師要多勉勵學生，讓他們多多交流觀點，相互討論，讓他們在相互交流、相互討論中尋求解題的思路與方法，讓學生善傾聽、敢發言、會表達，使學生主動參與，積極思考，進而培養學生的運算、推理、抽象等素養，幫助學生完善思維，培育理性思維。

變式教學中，教師要準確把握題目所要求的知識內容與能力培養的目標，要有目的、有意識地引導學生，使學生學會舉一反三。這樣才可以幫助學生融會貫通所學的知識，讓學生在變化中領略數學魅力，從而提高學生的數學應用能力及思維能力。

在課堂教學中，教師要把握好變式教學中的針對性、適應性、參與性原則，重視培養學生總結歸納分析問題的能力，讓學生能夠活學活用，培養學生的思維能力。教師通過變式教學點撥啟發引導學生去掌握新的知識，培養新的能力，在課堂教學中逐步地去培養并提高學生的數學核心素養。實踐表明，變式教學是一種促進學生數學核心素養發展的較為有效的教學模式。