時滯和擴散影響下社交網絡謠言傳播動力學*

王楠 肖敏? 蔣海軍 黃霞

1) (南京郵電大學自動化學院&人工智能學院,南京 210023)

2) (新疆大學數學與系統科學學院,烏魯木齊 830047)

3) (山東科技大學電氣與自動化工程學院,青島 266590)

提出了一個考慮空間擴散與發酵期時滯的社交網絡謠言傳播模型,重點研究了擴散與時滯對在線社交網絡中謠言時空傳播的影響.首先,分析了謠言傳播平衡點的存在性,并得到了基本再生數 R0 ;其次,運用Roth-Hurwitz 穩定判據分析了謠言傳播平衡點的局部穩定性,并討論了擴散誘導的Turing 不穩定;最后,選取時滯為分岔參數,建立了謠言傳播模型的Hopf 分岔條件.數值仿真結果表明,擴散和時滯的出現都能使得謠言傳播模型的穩定性發生根本性改變.本文從時間和空間兩個維度擴展了傳統謠言傳播動力學僅考慮時間演化的局限,更加真實地模擬了謠言在現實社會中的時空傳播規律,為謠言傳播的治理提供了全新的角度和思路.

1 引言

2022 年2 月,中國網民規模達10.32 億,互聯網普及率達73.0%,形成了全球最為龐大的數字社區.在線社交網絡的發展一方面使得網民之間的交流變得更加便捷,另一方面也為謠言傳播提供了新的途徑[1-3].網絡謠言傳播比傳統途徑傳播速度更快,范圍更廣,不加以阻斷可能會在短時間內占用大量社會資源,引發民眾恐慌甚至造成巨大的經濟損失[4,5].特別是在突發性公共衛生事件中,由于民眾對事件本身不了解,往往會被謠言和不實信息所吸引,甚至成為謠言傳播者,極大地破壞了社會的穩定[6,7].因此,定性和定量地研究社交網絡中虛假信息的傳播規律,成為謠言治理工作的重中之重.

如何建立符合現實的社交網絡謠言傳播模型受到廣大學者的高度關注.謠言在網絡中傳播具有隱蔽性強、傳播范圍廣、傳播途徑復雜以及傳播過程難以控制等特征,這與傳染病在人群中擴散有著極大的相似.因此,謠言經常被稱作互聯網中的傳染病.現有的網絡謠言傳播模型大多借鑒了傳染病模型[8-10].例如,利用傳染病動力學中倉室模型[11,12]的概念將社交網絡中的人群區分為謠言易感者、謠言已知者和謠言恢復者等基本類型,并在SIR (susceptible-infected-recovered)模型的基礎上建立起各類網絡謠言傳播模型.這些數學模型能夠精準而直觀地描述網絡謠言的傳播規律,充分而深刻地揭示網絡謠言傳播的危害.因此,基于傳染病模型的謠言傳播動力學已引起廣泛關注.例如,Moreno 等[13]在2004 年首次研究虛假信息在隨機無標度網絡中的擴散過程,通過對參數時間分布的數值計算區分不同的謠言傳播算法;Zhou 等[14]考慮網絡拓撲結構及感染節點的鄰近節點之間的差異對謠言傳播的影響,發現感染節點的總數取決于網絡的拓撲結構;張芳等[15]指出,謠言是一種典型的社會群體心理現象,在建立傳播模型時應引入心理學因素,如感知、情緒、記憶、決策等;趙來軍等[16]考慮了記憶因素對謠言傳播過程的影響,提出了具有遺忘機制的謠言傳播模型,并且發現網絡的平均度存在閾值,超過這個閾值,謠言的影響就會達到飽和;顧亦然和夏玲玲[17]注意到重要熟人免疫策略能有效地抑制謠言傳播,建立了新的SEIR (spreader-exposed-ignorant-recovered)謠言模型并根據真實在線社交平臺Facebook 的用戶數據進行數值模擬;萬佑紅和王小初[18]基于現實社交網絡中存在的從眾效應進行模擬仿真,研究個體影響力對謠言擴散的作用;朱霖河和李玲[19]在傳統的網絡謠言傳播模型中引入飽和辟謠函數用以刻畫政府辟謠行為對謠言傳播的約束能力;Ruan 等[20]研究在簡單傳播模型里引入智能節點研究惡意節點對謠言傳播的影響,結果表明惡意節點緊密度的增加會助長虛假信息的傳播;Chen 和Wang[21]將謠言未知者按性格分為穩重型未知者和激進型未知者,提出了新的SEIsIrR (spreader-exposed-steady ignorantradical ignorant-recovered)謠言傳播模型,通過對Twitter 上真實傳播的謠言數據集進行仿真,證明人的性格、謠言的可信度及謠言與生活的相關性影響著謠言傳播的范圍與速度.

隨著近些年移動互聯網設備的迅猛發展,人們早已突破時空限制,可以隨時隨地通過社交網絡參與到公共事件的討論中.因此建立反應擴散方程[22,23]來描述網絡信息的時空擴散變得具有現實意義.反應擴散網絡謠言傳播模型不僅能夠反映謠言的網絡分布特征,還可以描述其發展趨勢: 擴散項刻畫了網絡謠言在一維空間中沿著某一固定傳播方向進行擴散的過程;在傳播方向上的某一固定空間位置內,網民自行傳播謠言,由于位置不變,該過程與謠言傳播的時間緊密關聯.一些學者也建立了相應的反應擴散謠言傳播模型,研究其豐富的時空動力學特征.例如,趙洪涌和朱霖河[24]針對媒體報道與空間擴散等因素,建立了反應擴散SIM (spreader-ignorant-medium)謠言傳播模型,并給出系統穩定與Hopf 分岔產生的條件;Zhu 等[25]為了使得模型更加貼合真實的傳播機制,在反應擴散SI(spreader-ignorant)謠言傳播模型中加入非線性發生率βSI/(1+αI),并分析了擴散系數對謠言傳播穩態的影響.

在實際的網絡謠言傳播過程中,時間滯后同樣不可忽視.在網絡謠言從產生、傳播、治理到消失的各個階段中都可能存在著時滯[26,27].謠言剛出現時一般只在小范圍內傳播,但借助開放的社交網絡,其在人群的討論中醞釀發酵,甚至會在更大范圍內傳播.發酵期時滯指的是網絡謠言從產生到傳播的過程中會在謠言易感者群體中存在時間滯后的現象,忽視謠言傳播的發酵期可能會導致謠言治理的不及時.

但是目前同時考慮空間擴散效應與發酵期時滯的謠言傳播模型并不多見.為了更好地刻畫不同人群在謠言傳播模型中相互轉化的過程,本文考慮在謠言傳播過程中謠言未知者會以不同類型的發生率分別轉化為謠言感染者及恢復者,并且謠言感染者會在社交網絡中接收到辟謠信息從而轉化為恢復者.基于上述分析,從時空維度建立一個具有飽和發生函數、發酵期時滯以及擴散項的謠言傳播模型,研究時滯與擴散項對謠言傳播模型穩定性的影響.

本文結構組織如下.在第2 節中,提出一個具有擴散效應和時滯的謠言傳播模型.在第3 節中,對模型進行穩定性分析,并研究無時滯反應擴散謠言傳播模型的Turing 不穩定性.選取時滯為分岔參數,給出了模型在平衡點處發生Hopf 分岔的條件.在第4 節中,通過數值仿真來驗證前文的理論結果.在第5 節中,對本文工作進行總結并展望未來的工作.

2 模型建立

文獻[10]將網民分為謠言未知者S、謠言已知者I和謠言恢復者R這三種狀態,其描述的SIR謠言傳播模型如下:

其中,未知者S未收到謠言,已知者I收到謠言并傳播,恢復者R收到謠言但不傳播.由于社交網絡具有開放性,未知者S以Λ的人口輸入率自然增長,γ表示謠言在社交網絡上傳播的速率,接觸到謠言的未知者S以θ和 1-θ的概率分別轉為已知者I和恢復者R,辟謠信息以β的速度在社交網絡中傳播.同時三種狀態的網民均以μ的概率離開.考慮現實意義,以上參數均為正.文獻[10]通過計算給出了模型(1)的平衡點和基本再生數R0的表達式,討論該模型的穩定性和分岔點,并通過幾何方法分析了局部平衡點的全局穩定性.仿真結果表明,模型(1)在R0=1 處存在分岔,并且當R0＞1時,已知者I密度隨著R0的增加而逐漸增加;θ的變化對穩定狀態下I密度的峰值有較大影響,但對I密度的收斂時間影響較弱.這為謠言治理工作提供了新的思路.

然而模型(1)沒有考慮擴散和時滯對于網絡謠言傳播的影響.為了使模型更加貼合現實,我們在模型(1)的基礎上引入擴散項、時滯與飽和發生率.文獻[19]提出用飽和函數h(I)=βI/(1+αI)來描述辟謠信息在社交網絡中的傳播,其中β表示辟謠信息在社交網絡上的傳播速度,α是衡量已知者種群數量對于辟謠信息傳播效果的飽和因子,這與現實中網絡謠言的傳播規律十分貼合.于是得到了以下具有飽和函數的時滯反應擴散謠言傳播模型:

其中t＞0,x∈Ω=(0,π) .初始條件為

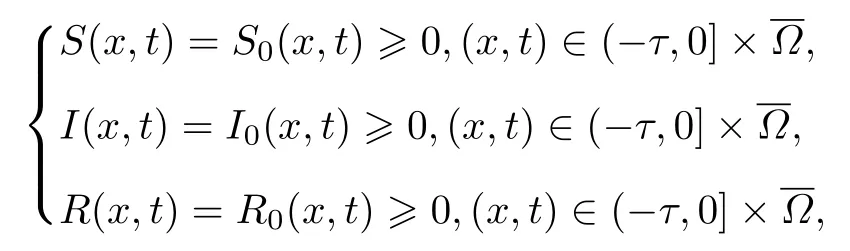
Neumann 邊界條件為

S(x,t),I(x,t)和R(x,t) 分別表示謠言未知者、謠言已知者和謠言恢復者在t時刻x位置處的密度.γS(x,t-τ)I(x,t)表示謠言已知者I在謠言未知者S種群中傳播謠言的能力,τ是謠言未知者S種群在接收到謠言后經過討論和思考而決定是否傳播謠言的反應時間.βI(x,t)/(1+αI(x,t)) 是辟謠信息在謠言已知者I數量的飽和作用下將謠言已知者I轉化為謠言恢復者R的辟謠能力.初始條件S0(x,t),I0(x,t)和R0(x,t)為非負連續函數.Δ=?2/?x2是拉普拉斯算子.d1＞0,d2＞0 和d3＞0分別是S(x,t),I(x,t)和R(x,t) 的空間擴散系數.Ω是一個有界域,?Ω是Ω的光滑邊界,η是?Ω的單位外法向量.Neumann 邊界條件表示謠言傳播系統是封閉的,謠言在網絡邊界沒有流進與流出.

3 時空動力學分析

根據現實意義,本文研究模型(2)的兩個非負平衡點:

(i)無謠言平衡點E0=(Λ/μ,0,0),此時模型(2)中僅存在謠言易感者,謠言未能在人群中傳播;

(ii)謠言傳播平衡點E*=(S*,I*,R*),此時存在謠言傳播者,謠言已在人群中持續傳播,其中

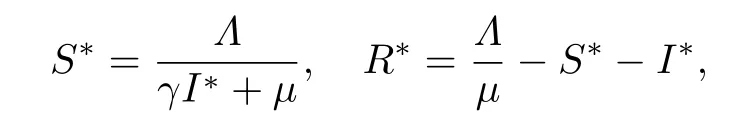
并且I*滿足方程

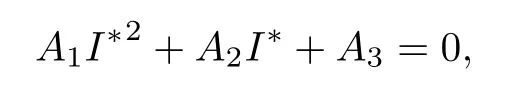
其中

假設:

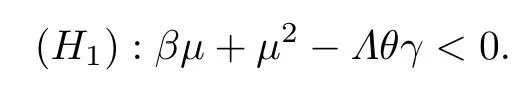
當 (H1) 成立時,則有

此時E*=(S*,I*,R*) 為模型(2)的唯一正平衡點.

基本再生數R0是謠言傳播模型中一個重要參量,用于衡量網絡謠言在人群中傳播擴散的能力.當R0＜1 時,謠言在人群中會自行消亡;當R0＞1時,謠言則會持續存在下去.本文根據文獻[28]的再生矩陣的方法計算R0.令X=(i,r)T,不考慮擴散項,由模型(2)可得

其中,

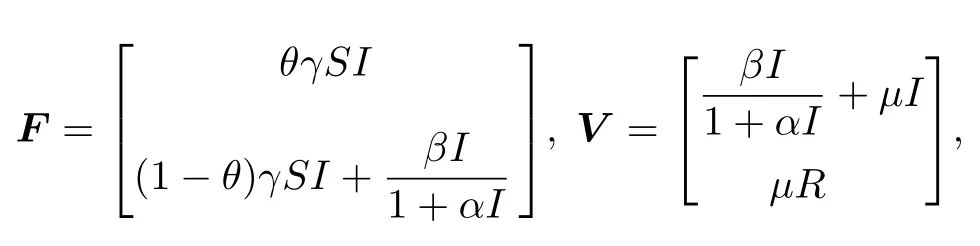
在無謠言平衡點E0處的雅克比矩陣分別為

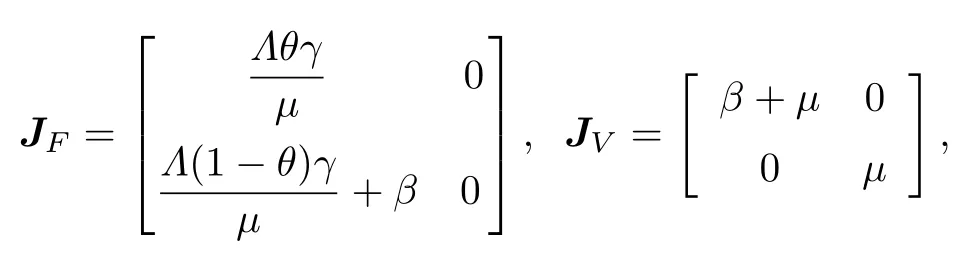
于是有

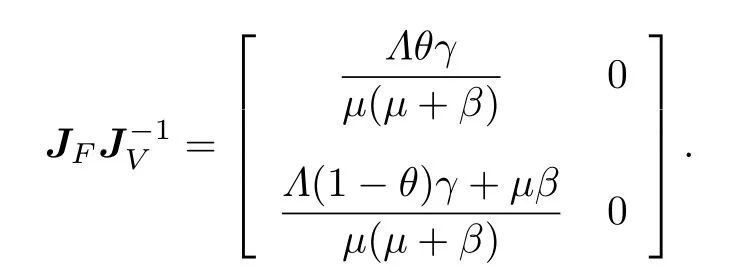
令

則模型(2)的線性化系統為

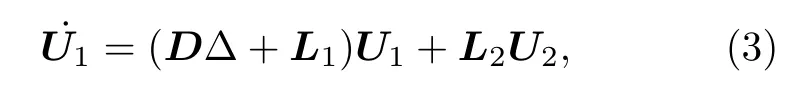
其中

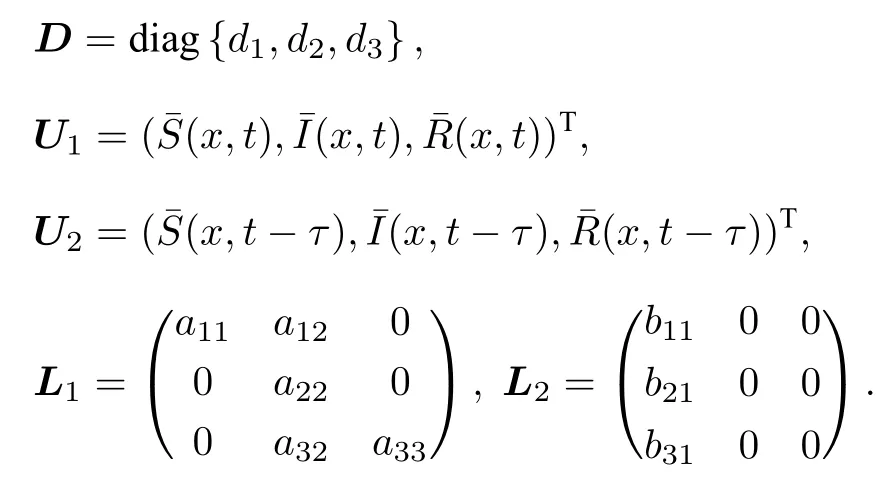
并且

對于所滿足的紐曼邊界條件,易知Δ 有特征值-k2(k∈{0,1,2,···}),模型(2)的特征方程為

其中I是 3×3 的單位矩陣,且

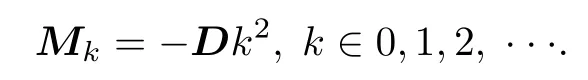
將特征方程(4)展開,得到如下表達式:

其中

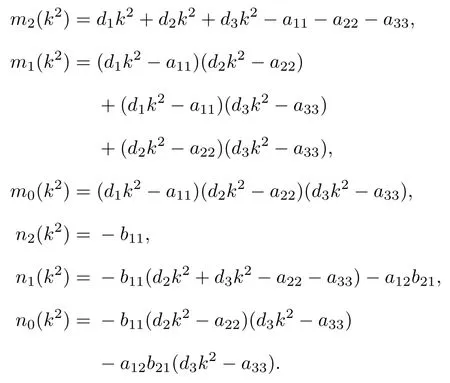
3.1 Turing 不穩定

本小節重點研究在無時滯的情形下,即τ=0時,擴散項對模型(2)穩定性的影響.

當無擴散,即d1=d2=d3=0 時,模型(2)在E*處的特征方程為

其中

由Roth-Hurwitz 穩定判據可知,當假設

成立時,方程(6)所有的根都具有負實部.因此,模型(2)在平衡點E*處是局部漸近穩定的.

當擴散效應出現時,即di＞0(i=1,2,3) 時,模型(2)在E*處的特征方程為

其中

并且

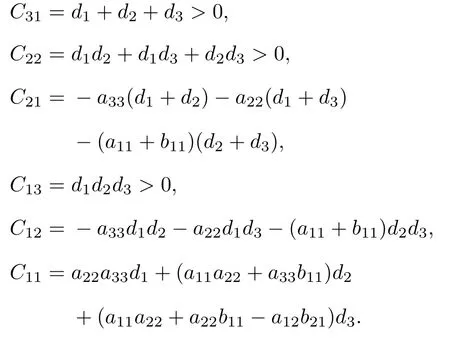
定義

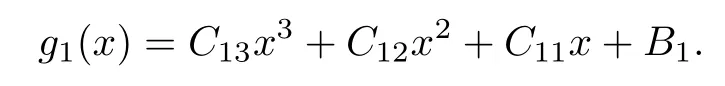
做如下假設:

其中

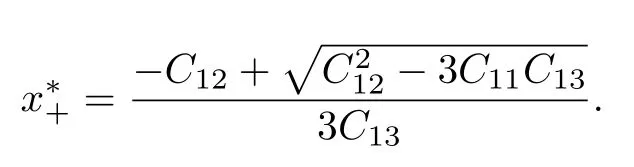
引理1當B1＞0 和 (H3)成立時,方程g1(x)=0有兩個正根x-和x+(0＜x-＜x+),使得當x∈(x-,x+)時,有g1(x)＜0 .

定理1假設R0＞1,τ=0,并且(H1)—(H4)成立.對于模型(2),以下結論成立 :

1) 當di=0(i=1,2,3) 時,模型(2)的謠言傳播平衡點E*是局部漸近穩定的;

2) 當di＞0(i=1,2,3) 時,模型(2)在謠言傳播平衡點E*處發生Turing 不穩定.

3.2 Hopf 分岔

本小節主要研究反應擴散謠言傳播模型(2)的時滯誘導Hopf 分岔.

當τ=0,di＞0(i=1,2,3) 時,模型(2)的特征方程為(7)式.做出如下假設:

由(8)式可知,若B3＞0 成立,則有C3(k2)＞0 ;若B2＞0 和 (H5)成立,則有C2(k2)＞0;若B1＞0 和(H5)成立,對于任意的x＞0 ,都有g1(x)＞0,于是得C1(k2)＞0.

計算可得

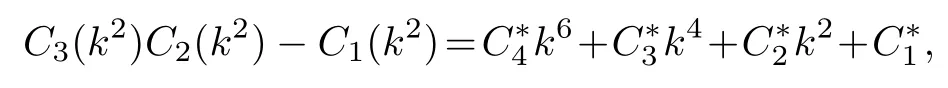
其中

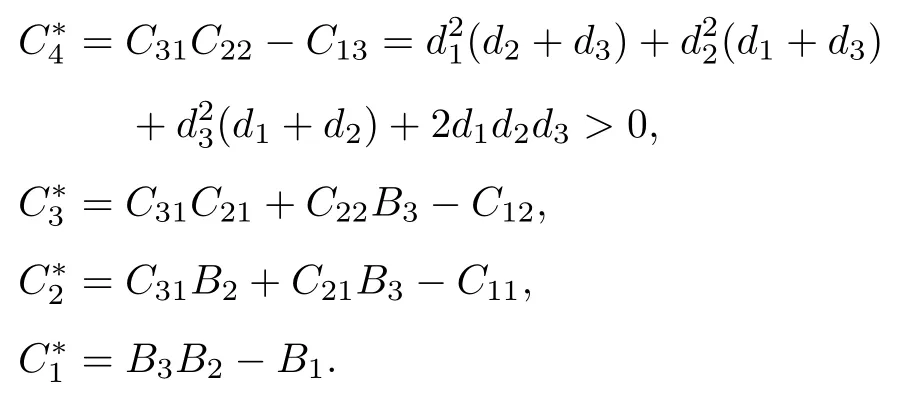
做出如下假設:

若B3B2-B1＞0 和 (H6)成立,則對任意k∈{0,1,2,3,···},有

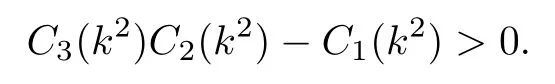
根據Routh-Hurwitz 穩定判據,若 (H2),(H5) 和(H6)均成立,對于任意的k∈{0,1,2,3,···},方程(7)的根均具有負實部.此時,無時滯模型(2)在謠言傳播平衡點E*處是局部漸近穩定的.

當τ＞0,di＞0(i=1,2,3) 時,模型(2)的特征方程為(5)式.令λ=iω(ω＞0) 并代入(5)式,分離實虛部得到

其中

根據 cos2(τω)+sin2(τω)=1 可得

其中

令z=ω2,則(10)式變為

令

當k=0 時,若以下條件成立:

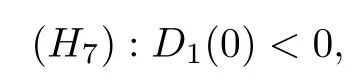
則有g3(0)|k=0=D1(0)＜0,且=+∞,根據零點定理可知,此時方程g3(x)|k=0=0內至少存在一個正根.不失一般性,假設方程g3(x)|k=0=0 存在三個正根xn(n=1,2,3),則特征方程(5)|k=0存在三個純虛根 iωn,其中ωn=(n=1,2,3).

由(9)式可得

其中

定義

當k≥1 時,令j=k2.定義

假設:

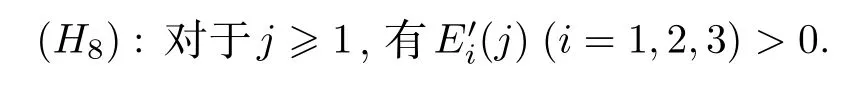
若 (H8)成立,那么當j≥1 時,Ei(j)(i=1,2,3) 是單調遞增的,有

做如下假設:

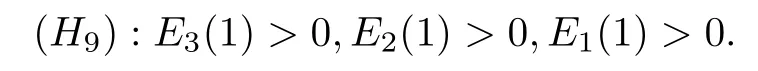
若 (H9)成立,則有Di(k2)=Ei(j)≥Ei(1)＞0(i=1,2,3),于是有方程(11)|k≥1無正根.

驗證k=0 時的穿越條件,對(5)式兩邊同時關于τ求導,于是有

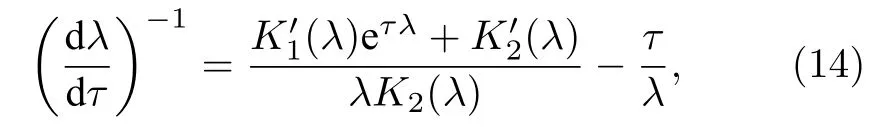
其中

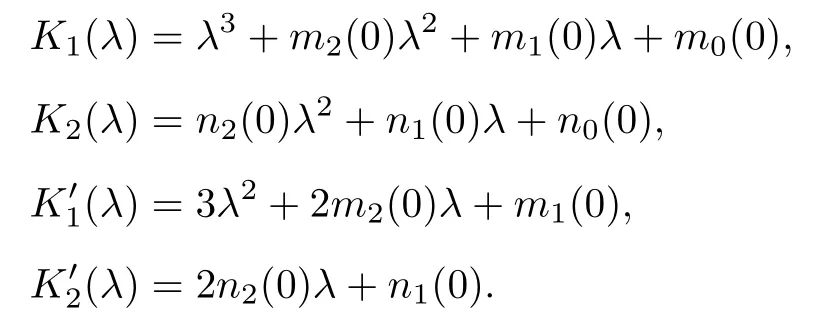
將τ=τ0和λ=iω0代入(14)式,得到

其中

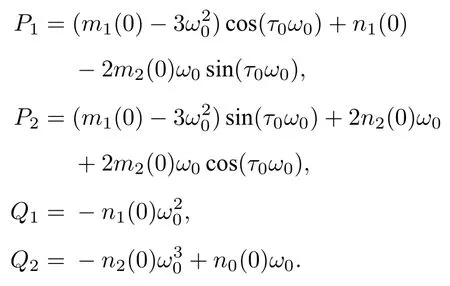
于是,

則,

做如下假設:

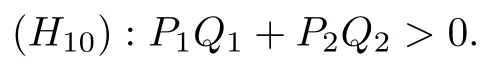
若滿足 (H10) ,則.基于上述討論,得到如下定理:

定理2假設R0＞1,di＞0(i=1,2,3),并且(H1),(H2),(H5)—(H10) 成立.對于反應擴散謠言傳播模型(2),以下結論成立:

1) 當τ∈[0,τ0)時,謠言傳播平衡點E*是局部漸近穩定的;

2) 當τ＞τ0時,謠言傳播平衡點E*是不穩定的;且當τ穿越τ0時,模型(2)在E*附近發生Hopf分岔.

4 數值仿真

本節在文獻[10]的基礎上選取參數,通過數值計算與分析來驗證上述理論的正確性,并研究謠言已知者I種群數量對辟謠信息傳播的飽和作用.

選取模型(2)的參數為Λ=0.8,γ=0.6,μ=0.3,α=0.5,β=0.2,θ=0.7.此時假設 (H1) 成立.通過計算得R0=2.24＞1 以及謠言傳播平衡點E*=(1.0595,0.7584,0.8487).

下面首先研究空間擴散對無時滯謠言傳播模型穩定性的影響,此時τ=0.研究選取的初始條件為S(x,0)=1.0595+0.1cosx,I(x,0)=0.7584+0.1cosx,R(x,0)=0.8487+0.1 cosx.當d1=d2=d3=0 時,通過驗證可以得到假設 (H2) 成立.由定理1 可知,模型(2)平衡點E*處是局部漸近穩定的,數值仿真結果如圖1 所示;當d1=6,d2=0.01,d3=0.01 時,通過驗證知假設 (H3) 和 (H4) 均成立.根據定理1,模型(2)在E*處失去其穩定性,發生Turing 不穩定,數值仿真結果如圖2 所示.圖3 是模型(2)發生Turing 不穩定時的Turing斑圖.

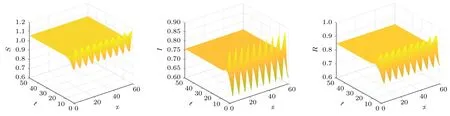
圖1 當 τ=0,d1=d2=d3=0 時,模型(2)在 E* 處是局部漸近穩定的Fig.1.Model (2) is locally asymptotically stable at E* when τ=0,d1=d2=d3=0.

圖2 當 τ=0,d1=6,d2=0.01,d3=0.01 時,模型(2)在 E* 處是不穩定的Fig.2.Model (2) is unstable at E* when τ=0,d1=6,d2=0.01,d3=0.01.

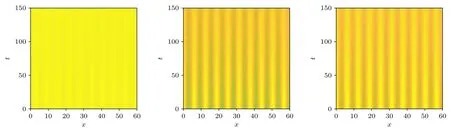
圖3 Turing 不穩定發生時模型(2)的Turing 斑圖Fig.3.Turing patterns of model (2) when Turing instability occurs.

從圖1 可以看出,在無擴散時,隨著時間的推移,社交網絡中未知者S、已知者I和恢復者R這三類人群的密度分別快速收斂于1.0595,0.7584和0.8487,這說明謠言在人群中穩定持續地存在著.從圖2 可以看出,引入擴散項后,謠言傳播在空間上呈現周期振蕩的趨勢,這意味著謠言于短時間內大規模地在社交網絡中快速地傳播開來.

其次,驗證由時滯誘發的Hopf 分岔.令d1=d2=d3=0.1,并選取初始條件為S(x,0)=1.25,I(x,0)=0.85,R(x,0)=0.74.計算可知此時ω0=0.5513,τ0=2.6332,通過驗證可以得到假設(H5)—(H10)均成立.根據定理2,當τ=2.6＜τ0=2.6332時,模型(2)在E*處是局部漸近穩定的,仿真結果如圖4 所示;當τ=2.655＞τ0=2.6332 時,模型(2)在E*處變得不穩定,仿真結果如圖5 所示.

從圖4 和圖5 可以看出,當時滯τ小于分岔閾值τ0時,三種狀態的網民密度趨于固定值,這表明此時人群中始終存在固定數量的謠言已知者;當時滯τ大于分岔閾值τ0時,三種狀態的網民密度呈現出周期振蕩,意味著謠言在社交網絡中持續存在且周期性地傳播,在增加謠言治理難度的同時也帶來了新的風險.圖6(a)是τ=2.6 時模型(2)在位置x=4 處的相圖,圖6(b)則是τ=2.655 時模型(2)在位置x=4 處的相圖.

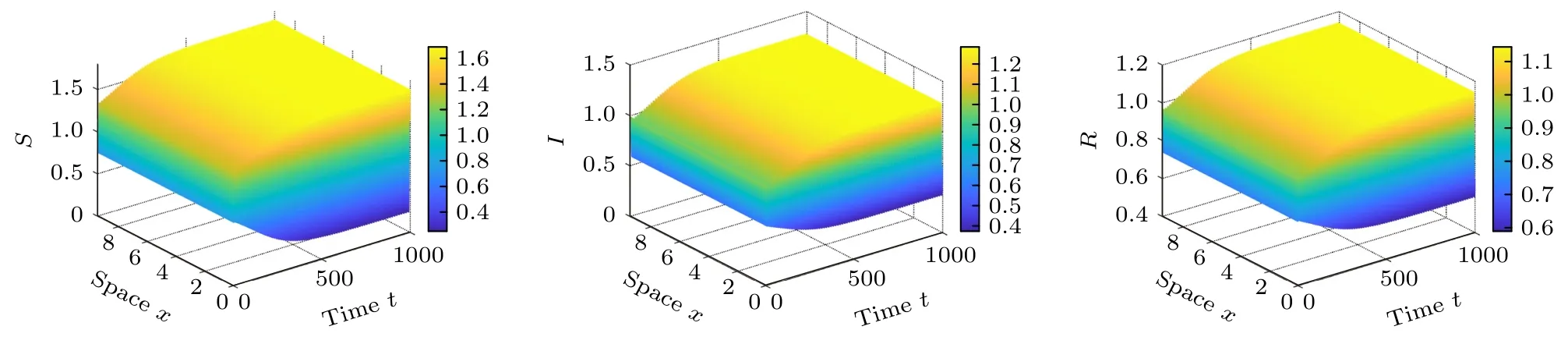
圖5 當 τ=2.655＞τ0=2.6332 時模型(2)的波形圖Fig.5.Waveform plots of model (2) with τ=2.655＞τ0=2.6332 .

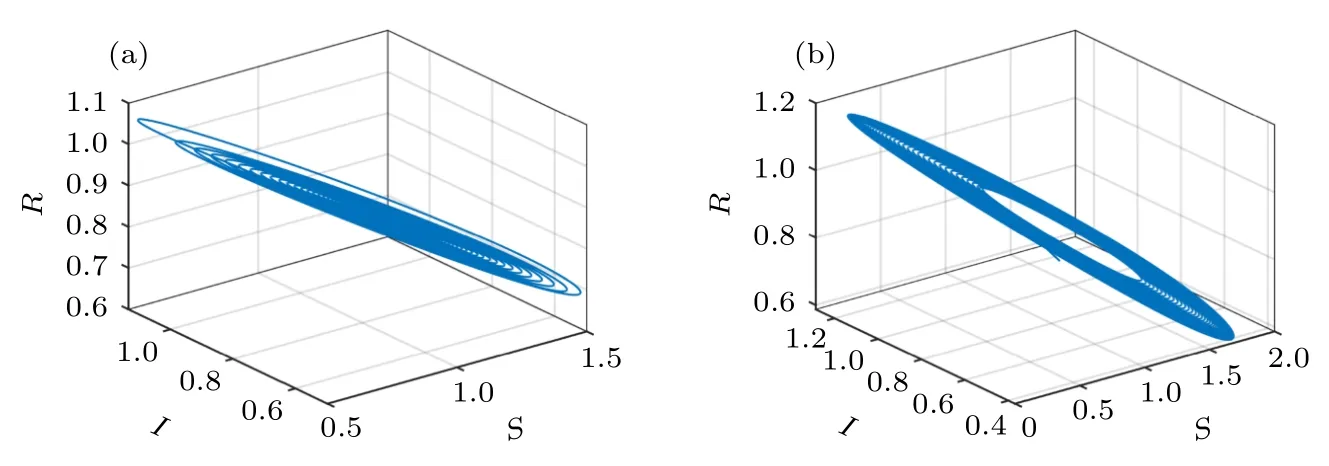
圖6 模型(2)在位置x=4 處的相圖 (a) τ=2.6;(b)τ=2.655Fig.6.Phase diagram of model (2) at x=4: (a) τ=2.6;(b) τ=2.655.

最后,研究飽和因子α對模型(2)穩定性的影響.為方便討論,取d1=d2=d3=0,其他參數不變,選取不同的α.從表1 可以看出,隨著I種群數量的飽和因子α增大,對辟謠效果的抑制作用也增大,人群中謠言已知者I的密度變大,謠言未知者S和恢復者R的密度則減小,并且謠言在社交網絡中發酵期時滯的分岔閾值τ0減小.

表1 不同α 對應的平衡點與分岔閾值Table 1.Equilibrium point and bifurcation threshold for different α.

圖7 是τ=2.4 時謠言已知者I的密度在α不同取值情況下的波形圖.顯然,α的增大不僅會使得謠言在更大范圍內傳播,還會延長謠言從產生到趨于穩定的時間,并且帶來更大的傳播峰值.

圖7 不同α 取值時I 的波形圖Fig.7.Waveform of I with different values of α.

5 結論

本文將發酵期時滯、空間擴散以及飽和辟謠函數引入到傳統SIR 謠言傳播模型中,研究了謠言在社交網絡中傳播的時空動態演化特性.首先,在穩定的無時滯謠言傳播模型中引入擴散項,給出模型發生Turing 不穩定的條件,證明了Turing 不穩定正是由擴散誘導的.其次,選取發酵期時滯作為分岔參數,給出模型產生Hopf 分岔的條件及分岔閾值τ0的表達式.當τ＜τ0時,含有擴散項的謠言傳播模型是穩定的;當τ＞τ0時,模型失去穩定性并發生Hopf 分岔.最后,在數值仿真部分驗證了前文的結論,并且模擬了I種群數量的飽和因子α對于謠言傳播的影響.α的增長表示I出現嚴重的擁擠現象,辟謠效果被削減,分岔閾值τ0減小,傳播峰值增大.這些結論為謠言預防和治理提供了新的理論依據.因此,監管仍處于發酵期的謠言,提高辟謠信息發布的時效性,加大對特定人群的辟謠力度,是構建良好社交網絡環境的重要內容.當前,本文主要研究的是時間滯后與空間擴散對社交網絡中謠言傳播的影響,在未來的工作中將進一步考慮多渠道對謠言傳播的影響并繼續研究分岔方向與分岔周期解的穩定性.