改進的QPSO 算法在自融資投資組合中的應用

何 光, 盧小麗, 李高西

(1. 重慶工商大學經濟社會應用統計重慶市重點實驗室，重慶 400067;2. 重慶工商大學數學與統計學院，重慶 400067;3. 重慶工商大學長江上游經濟研究中心，重慶 400067)

0 引言

在粒子群優化(Particle Swarm Optimization, PSO)算法[1]中，粒子的飛行速度受到取值邊界的限制，導致了粒子的搜索不能遍歷整個解空間，從而無法實現算法的全局收斂性。Sun 等人[2]研究發現，在量子空間中粒子的行為和人類的學習行為類似，具有很高的不確定性。于是，從量子力學的角度提出了一種改進的PSO 算法–量子行為粒子群優化(Quantum Particle Swarm Optimization, QPSO)算法。QPSO 算法的粒子更新只有位置方程，形式更簡單，控制參數更少，收斂速度和全局收斂性能更優，是PSO 算法中的一個較成功的改進，具有很強的理論意義和實際應用價值。然而，在實際計算時，粒子的搜索只是在可行解的空間進行搜索，導致粒子在迭代后期仍然會出現早熟和陷入局部最優點。因此，QPSO 算法仍具有很大的改進空間。

為了增強算法中粒子的全局搜索能力和算法的收斂速度，進一步提高優化問題解的精度，先后有學者提出了各種搜索策略和改進方法，以提升粒子的探索能力，避免算法陷入局部最優的困境。在QPSO 算法收斂性的分析中，Sun 等[3]和方偉等[4]討論了粒子迭代公式的參數選擇，他們的研究結果提升了算法的全局搜索能力。章國勇等[5]將精英學習策略加入到算法的改進中，更好地兼顧了算法的全局搜索和局部搜索能力。趙吉和程成[6]提出了一種基于演化搜索信息的改進算法，在拓展粒子搜索空間的同時，有效改善了算法的收斂精度。另外，部分學者在QPSO 算法的性能改進和應用方面，也取得了一些較好的研究結果[7–11]。

本文在已有研究的基礎上，準備從兩個方面對QPSO 算法進行改進。第一，在粒子的歷史位置更新公式中，考慮L′evy 搜索策略，以增強粒子的收斂速度，提高粒子的全局搜索能力和算法精度。第二，考慮混合概率分布的操作，幫助粒子在迭代后期脫離局部極值的束縛，增強種群的多樣性，避免算法陷入早熟。隨后，將改進的QPSO 算法應用到一類自融資投資組合問題中。

1 改進的QPSO 算法

1.1 QPSO 算法原理

在原始PSO 算法中，令xij和vij分別表示第i個粒子位置和速度的第j維，第i個粒子的歷史最優位置pbest 的第j維和全局最優位置gbest 的第j維分別記為pij(t)和pgj(t)。粒子的速度按照以下公式進行更新其中w為慣性權重，c1和c2為加速因子，r1和r2為0 到1 之間均勻分布的隨機數。

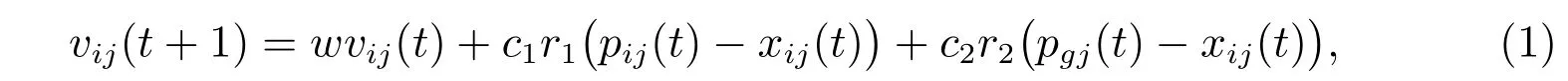
然而，QPSO 算法的更新公式中，不涉及粒子的速度公式，而采用蒙特卡羅法模擬粒子的運動狀態，更新不同時點的粒子位置。在粒子的迭代過程中，每個粒子會聚集到一個局部吸引點Pij(t)，速度更新公式(1)將變成吸引點的位置公式

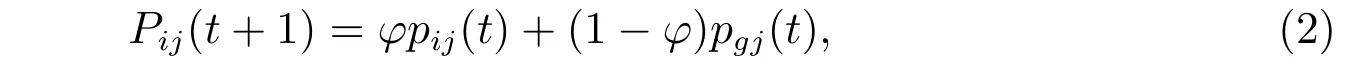
其中φ=c1r1/(c1r1+c2r2)。采用文獻[12]中的方法得到粒子的位置更新公式

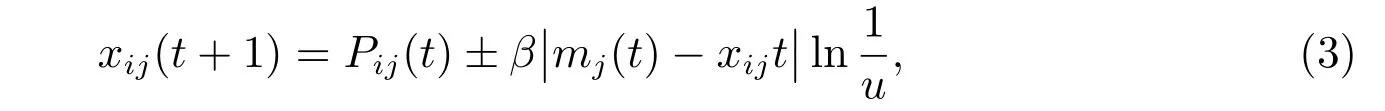
其中mj(t)表示粒子歷史最優位置的平均值的第j維，稱為平均最好位置。u表示0 到1 之間均勻分布的隨機數，當u大于0.5 時，公式(3)中取“+”，否則取“?”。β稱為收縮-擴張系數，用來調節粒子的速度，采用線性遞減公式，具體如下

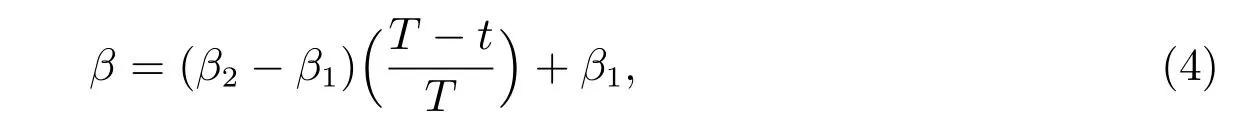
T表示最大迭代次數，β1和β2分別為β的最小值和最大值。

1.2 L′evy 飛行策略

作為一種隨機游走過程，L′evy 飛行策略有一個帶有寬尾的概率分布，這使得它的搜索方式具有很好的擾動能力，能夠大大提高算法的全局搜索性能和收斂精度。在搜索空間中，可以充分發揮L′evy 飛行的特點對粒子的運動方式進行改善，一方面利用其深入的短距離搜索有效提高算法的收斂精度，另一方面結合偶爾的長距離搜尋擴大粒子的探索空間，進而增強算法的全局搜索能力。

運用L′evy 飛行策略對粒子的位置更新公式(3)，作如下改進

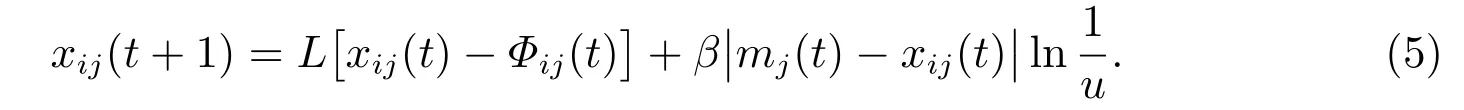
當u> 0.5 時，采用(5)式進行粒子位置的更新，其中L表示L′evy 隨機步長，采用Mantegna[13]提出的公式

其中μ ～N(0,),υ ～N(0,)為服從正態分布的隨機數，使用Gamma 函數Γ(·)，可得標準差滿足以下公式

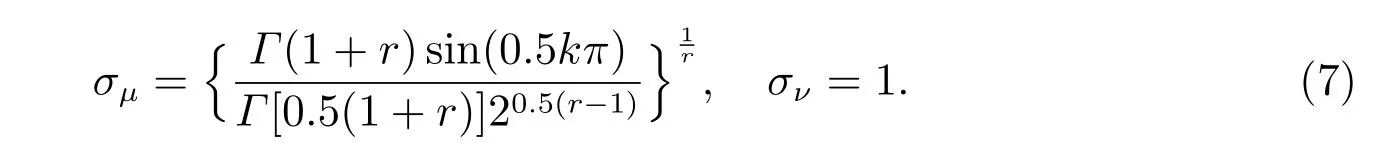
1.3 混合概率分布

隨著迭代進入后期，QPSO 算法中一些相似粒子會出現局部聚集的情況，從而大大減少算法的搜索范圍，導致算法早熟，這種情況與算法中吸引勢阱模型的分布選擇有著極大的關聯。Sun 等[14]通過實驗顯示，QPSO 中勢阱模型對應的指數分布在測試中有很好的實用性。然而，一些仿真結果表明具有正態分布的QPSO 算法在處理早熟問題上有著更好的表現。于是，可以考慮將兩種分布結合起來，用于改善算法在迭代后期容易陷入局部最優的困境。

考慮將正態分布和指數分布結合運用到粒子的位置更新中，形式如下

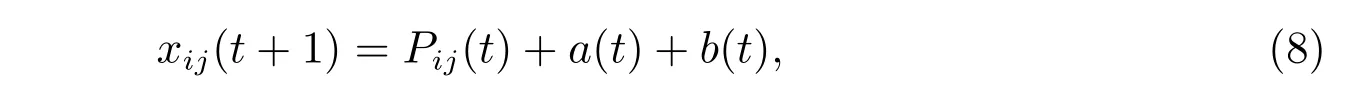
其中a(t)和b(t)分別為服從正態分布和指數分布的兩個隨機序列，具體的公式為

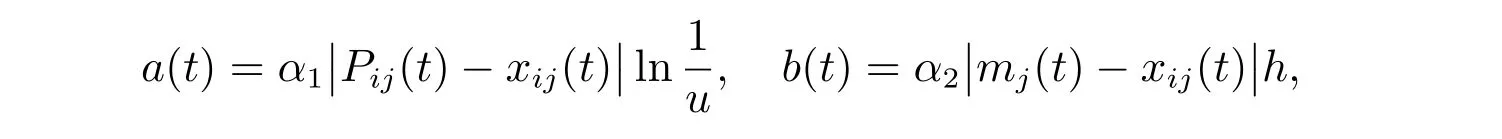
這里h為服從標準正態分布的隨機數，α1和α2均為收縮擴張系數。

1.4 算法流程

在QPSO 算法的改良中，融合了L′evy 飛行和混合概率分布這兩種手段。于是，將該算法簡記為HQPSO，算法的流程如下。

算法1HQPSO 算法

?

if u>0.5運用公式(6)計算L′evy 步長通過公式(se 通過公nd if 5)更新xij(t)el式(8)更新xij(t)e運用比較原則更新pbest 和gbest end for end while輸出結果

2 算法測試

2.1 測試函數及參數設定

在性能測試中，將HQPSO 算法與標準的QPSO 算法以及兩種優化效果較好的算法MDE 算法[15]和distABC 算法[16]進行比較。基準測試函數來源于CEC2005，其中f1～f6為高維單模函數，f13～f14為低維單模函數，主要用于測試算法的收斂精度；f7～f12為高維多模函數，f15～f16為低維多模函數，用于檢驗算法的全局尋優能力和局部搜索性能。其中f14的最優值為?1，其他測試函數的最優值均為0。

在對比實驗中，各算法的參數設置均來源于相關文獻。QPSO 算法中，β1和β2分別取0.4 和0.9。MDE 算法中，CR=0.4，F為隨機數。distABC 算法中，limit=(種群數×維度)/2。HQPSO 算法中，β1和β2分別取0.4 和0.9，隨機步長的參數r= 1.5。在對比測試中，高維函數中除f4取32 維外，其余均為30 維，低維函數都為2 維。各算法種群為50，最大函數評價次數為80 000，各算法對每個函數分別獨立運行30 次，取結果的最好值、均值和方差，具體數據見表1 和表2。

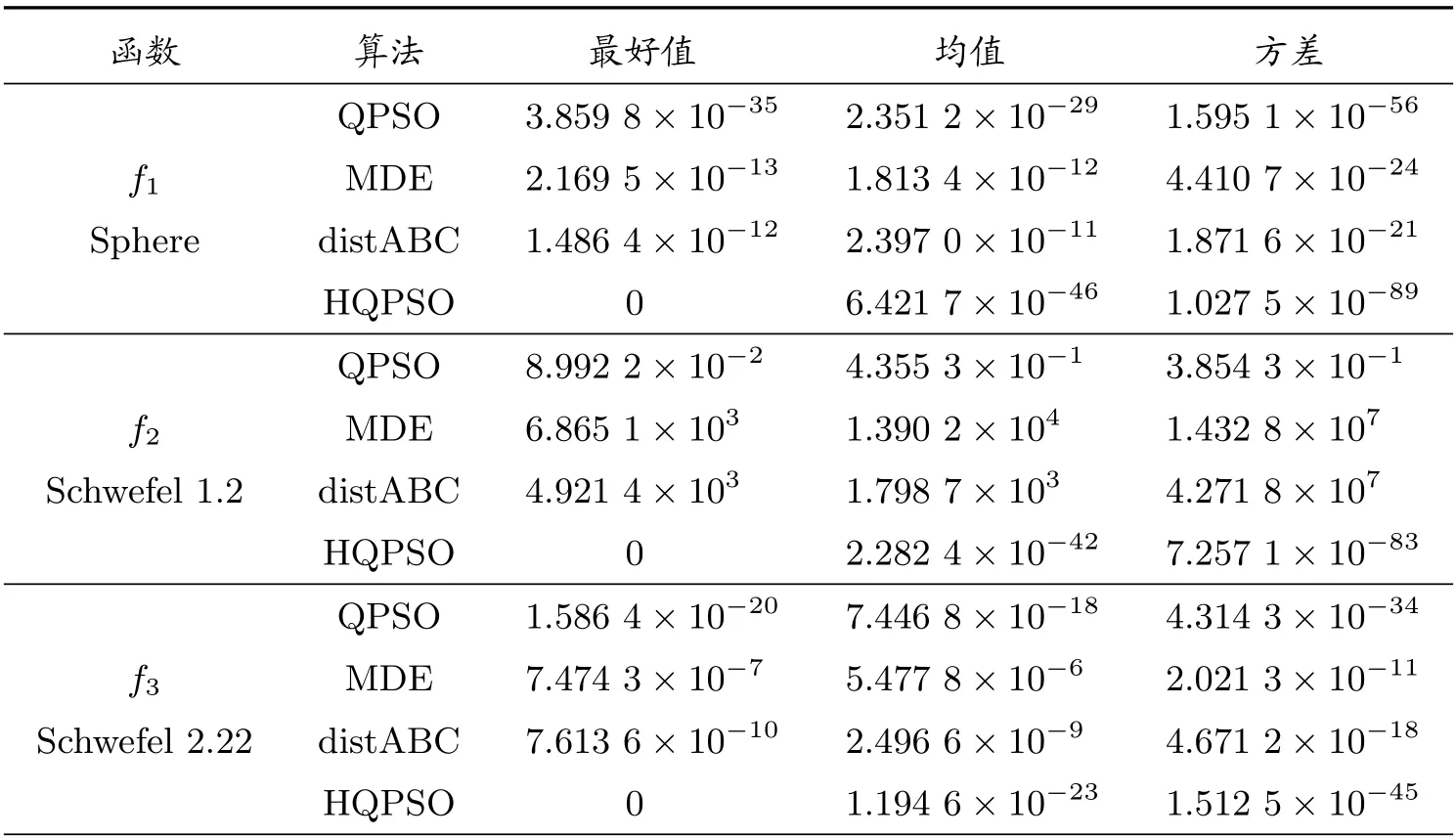
表1 f1 ～f8 測試結果

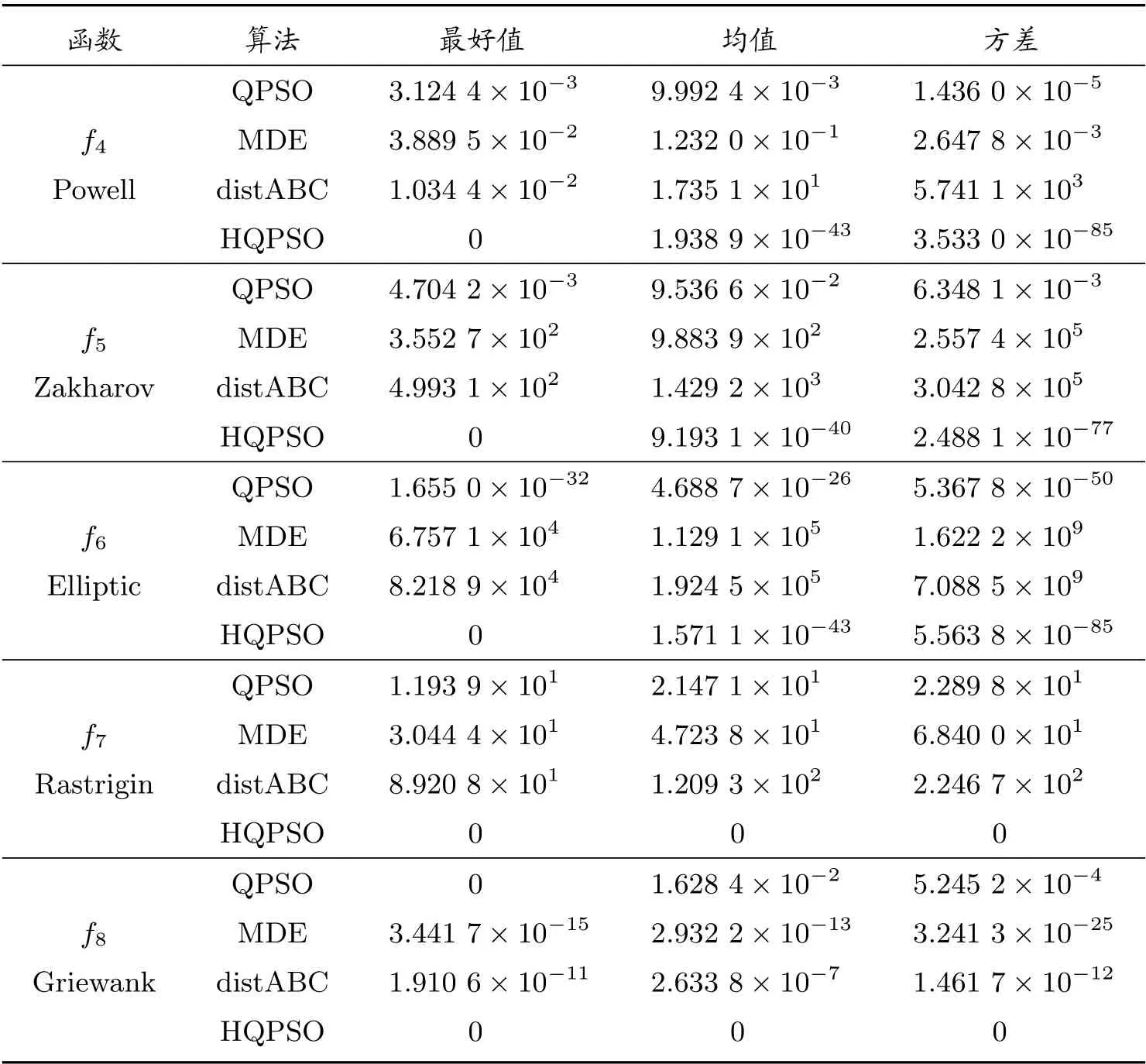
續表

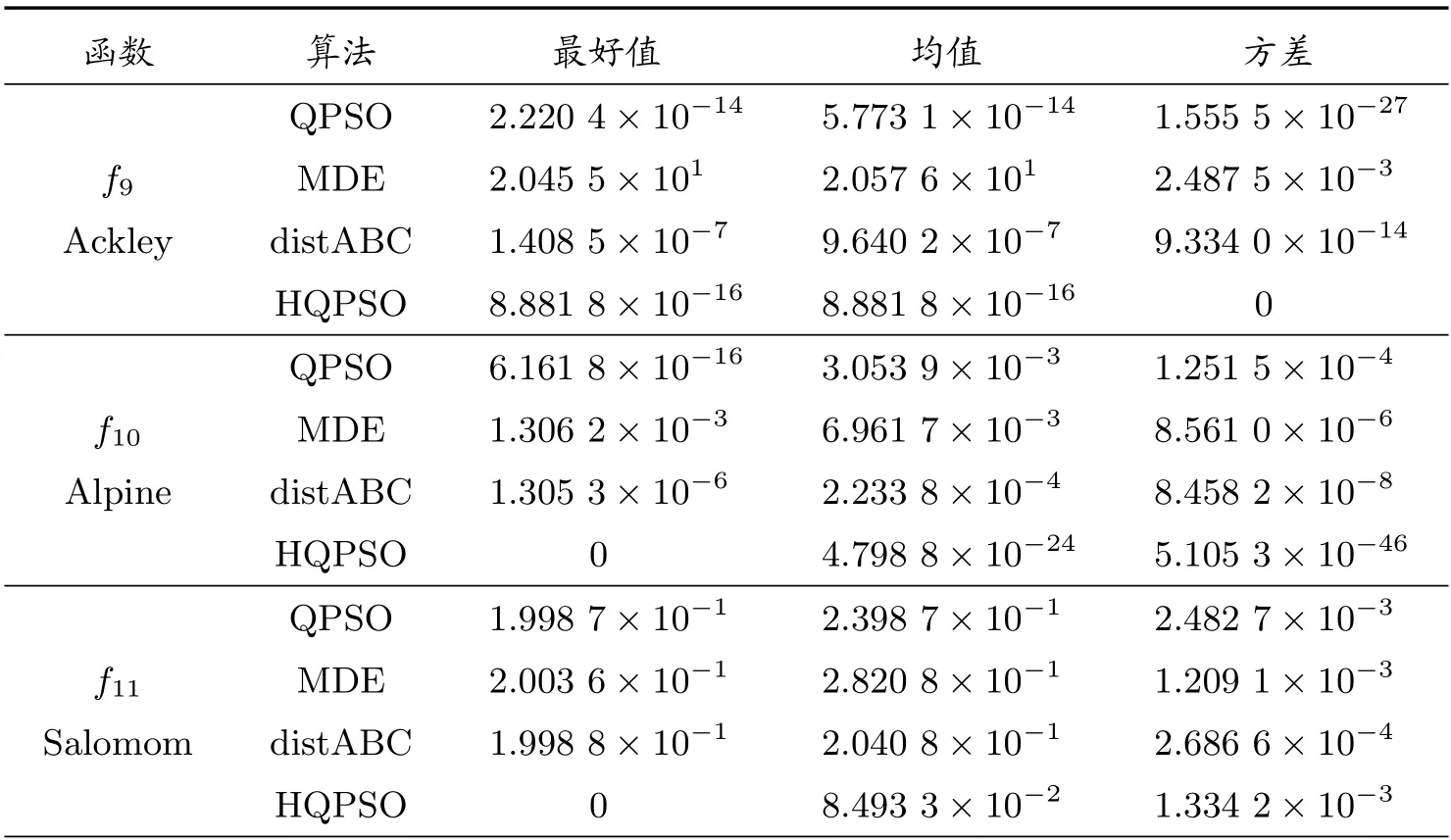
表2 f9 ～f16 測試結果

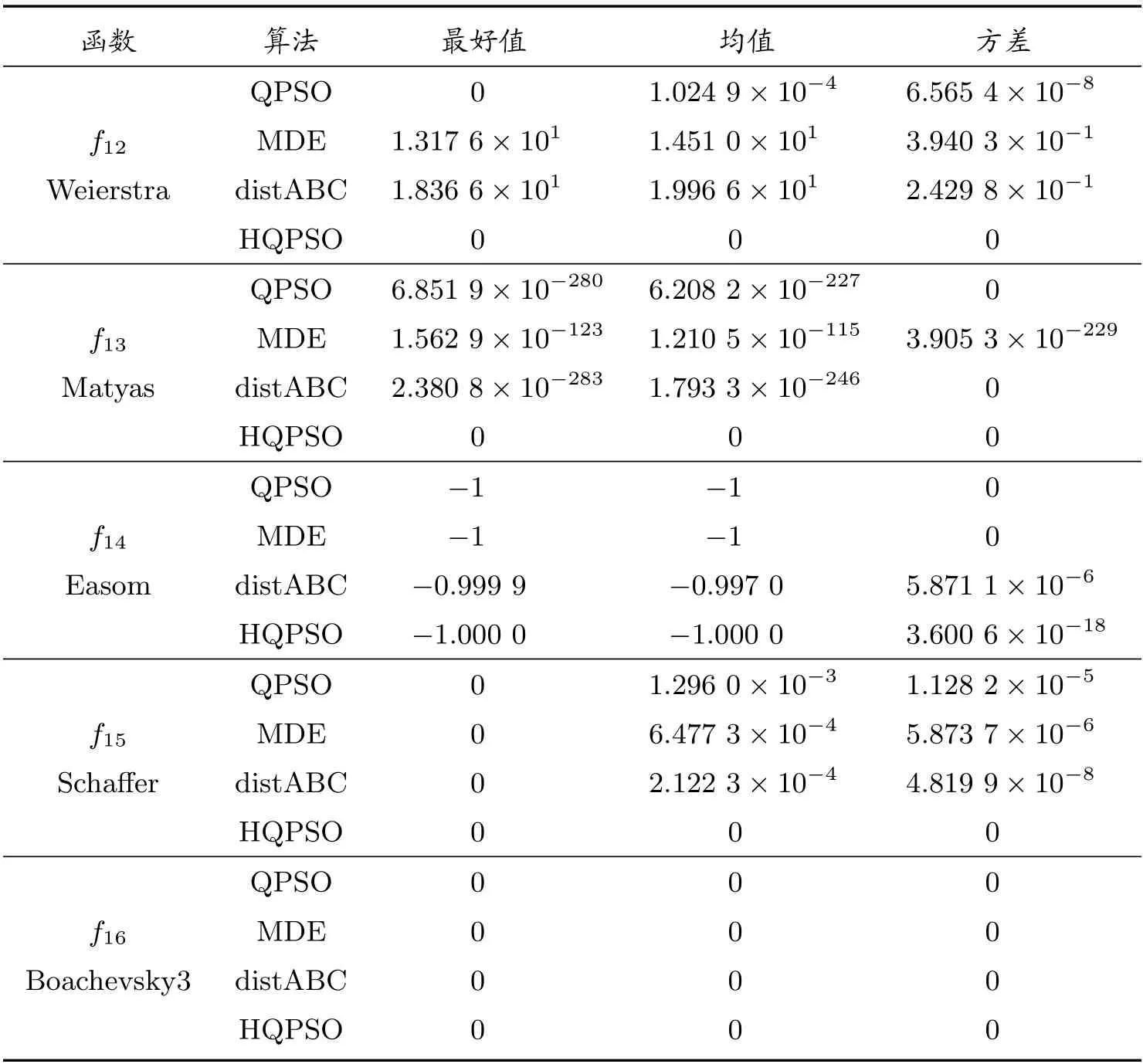
續表

2.2 算法的收斂精度分析

由表1 和表2 可見，HQPSO 在f1～f6以及f13～f14等單模函數上的精度幾乎都達到了10?10以上的數量級，在f13上取得了理論最優值。由于改進算法在粒子的迭代位置中引入了L′evy 飛行策略，使得粒子在搜索空間中更有效移動，提高了算法的收斂速度，在局部尋優能力上有明顯的增強。HQPSO 在f7～f12以及f15～f16等多模函數上同樣表現出色，在f7～f8、f12和f15～f16上取得了理論最優值。因為在算法中考慮了混合概率分布的特點，讓粒子以一定概率發生突變，在確保其全局搜索能力時，增強了種群的多樣性，從而使得算法可以及時跳出局部最優，避免早熟。于是，HQPSO 算法在單模和多模函數上，其收斂精度和穩定性均有優異的表現。

隨后，對比四種算法在高維和低維測試函數上的優化結果。HQPSO 在所有高維函數中的表現均優于其余三種算法。QPSO、MDE 和distABC 算法在12 個高維函數中都不能取到理論最優值，在f8～f12等5 個函數上三種算法都出現了早熟現象，優化結果不理想。相比之下，HQPSO 在f7～f8和f12上30 次測試均能取得理論最優值，而在其余的高維函數上也有一定的幾率搜索到理論最優值。在高維函數測試中，除了獲得更好的均值外，HQPSO 算法取得的方差也更小，表明該算法的穩定性更高。在低維函數測試中，除了f14外，HQPSO 算法均取得了理論最優值。MDE 算法在f14和f16上取得了理論最優值，然而，在f13和f15上未能取得理想的收斂結果。distABC 算法僅在f16上取得了理論最優值，在其余的低維函數中表現欠佳，對f14的測試中則陷入了局部最優。因此，在低維函數測試上，HQPSO 算法的綜合表現更好。

2.3 算法的魯棒性分析

進一步，比較四種算法的魯棒性。分別記錄各算法在測試函數f1～f15上收斂到10?10，以及在f16上收斂到10?10～1 的成功率，結果見表3。

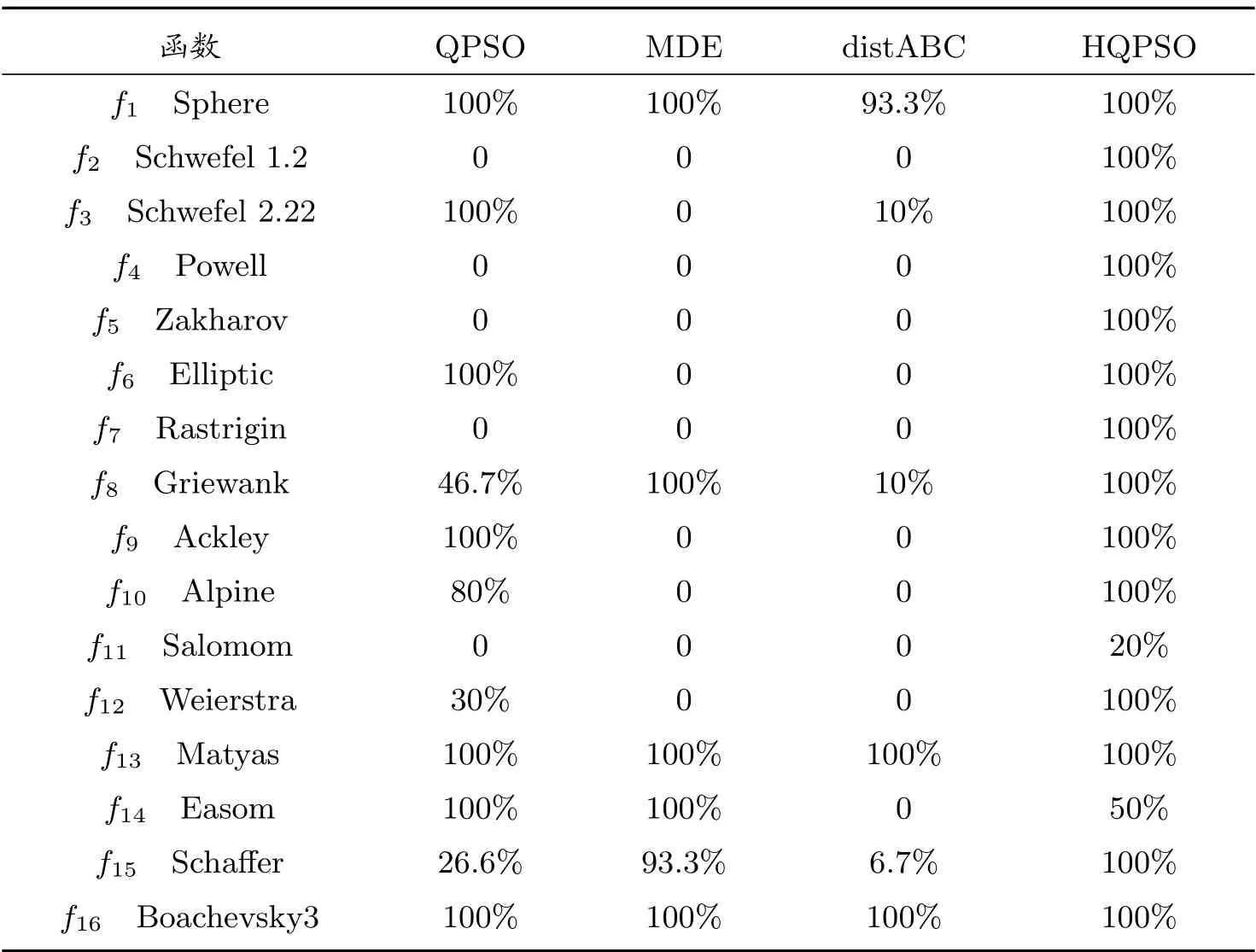
表3 魯棒性結果

由表3 可見，在16 個測試函數中，除了f11和f14，HQPSO 算法在30 次運行中的成功率均到達了100%，表明該算法具有較好的魯棒性。相比而言，QPSO、MDE 和distABC三種算法在低維測試函數上有較好的魯棒性，而MDE 和distABC 算法在大多數高維測試函數上成功率低，甚至為0。綜合來看，HQPSO 算法的魯棒性整體表現更出色。

2.4 算法的統計檢驗

隨后，為了驗證HQPSO 算法的有效性，將HQPSO 算法與其他三種算法兩兩進行Wilcoxon 符號秩檢驗，計算出配對算法的概率P值。另外，根據各種算法的Friedman秩均值在不同測試函數中的排名，得到四種算法的平均名次。具體的檢驗結果見表4。

由表4 可知，在Wilcoxon 檢驗中，HQPSO 與三種算法配對比較的概率值均小于0.01，意味著改進算法和其他算法有顯著差異。從Friedman 檢驗的平均排名結果可見，QPSO 算法在高維函數中的整體表現僅次于HQPSO，而在低維函數的測試中QPSO、MDE 和distABC 三者表現較接近。從總體上看，HQPSO 在所有測試函數中的綜合排名最高，性能更均衡。

表4 非參數檢驗結果

3 應用實例

3.1 自融資投資組合問題

經典的Markowitz 均值-方差模型為一類多目標優化問題，要求投資者在證券投資過程中選擇風險最小和收益最大的組合。自融資投資組合指除了初始的投資外，在投資過程中不追加任何投資，也不從中轉移資本，僅僅根據資產組合本身的收益變化情況進行組合的結構調整。自融資投資組合在套利、資產交換、市場中性投資、市場定時等方面有著廣泛的應用。考慮如下的自融資投資組合模型

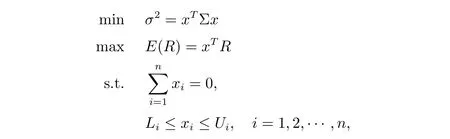
其中R= (R1,R2,···,Rn)T為組合的收益率向量，x= (x1,x2,···,xn)T為組合的權重向量，Σ 表示各種資產間的協方差矩陣，E(R)和σ2分別表示投資組合的預期收益率和風險，Li和Ui分別表示各種資產投資比例的下界與上界。

我們將以上優化模型轉化為無約束的優化模型，形式如下

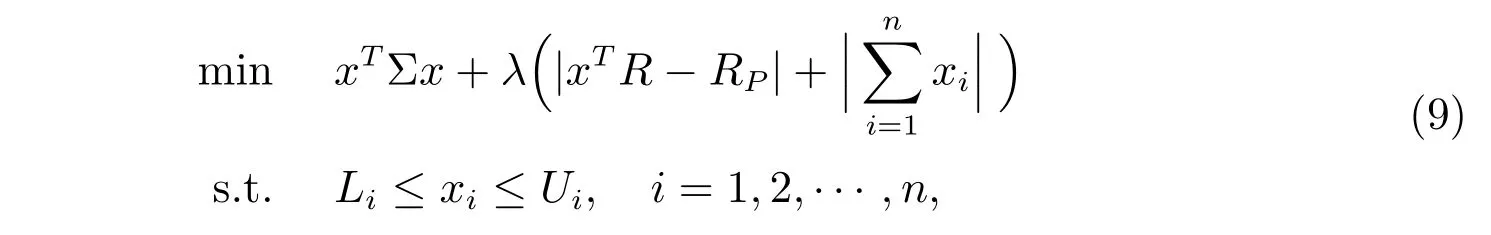
其中RP表示組合的預期收益率，其中λ為懲罰因子，在實驗中取值為10。

3.2 結果與分析

在數值實驗中，HQPSO 算法的參數設定與性能測試中相同，粒子總數為30 個，最大迭代次數為1 000 次，求解結果取30 次實驗的平均值。在實驗數據的選擇上，抽取了A 股市場中的15 只股票，以歷史收益率的平均值作為其預期收益率。各股票之間的方差-協方差矩陣，如表5 所示。預期收益率具體數據分別為：4.36%、3.58%、4.55%、8.91%、5.78%、8.79%、8.05%、3.54%、4.11%、3.87%、15.29%、3.65%、3.73%、12.61%、5.06%，初期的投資占比分別為：10%、10%、10%、0、10%、0、0、10%、10%、10%、0、10%、10%、0、10%。

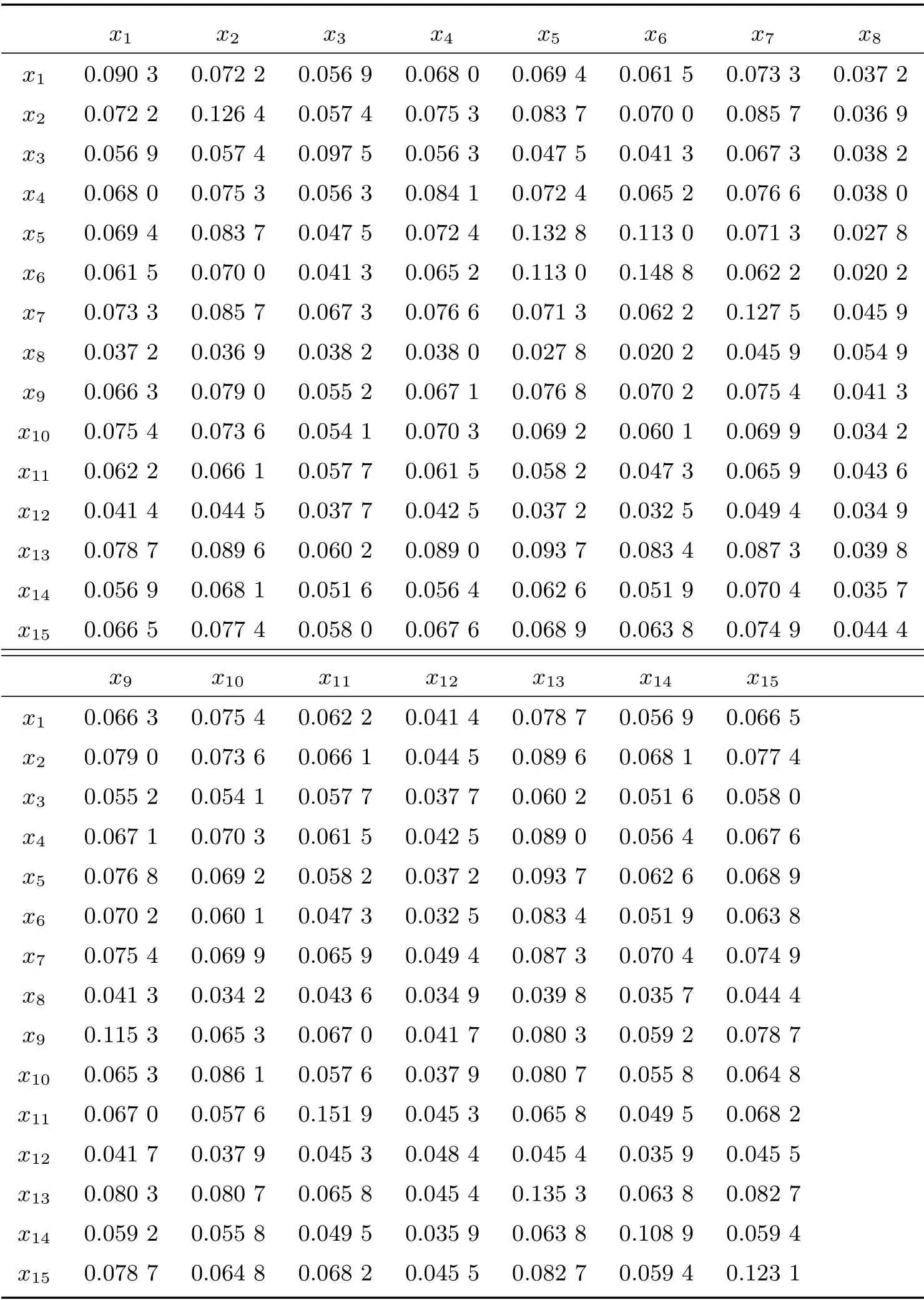
表5 方差-協方差矩陣

投資者希望原有投資額不變時，考慮將其他十支股票的投資合理分配到第4、6、7、11和14 這5 支股票上，在不允許賣空情況下尋求該自融資模型的解。表6 展示了在給定預期收益率時，投資組合模型(9)的最優解。通過給定的RP(在最小與最大預期收益率之間均勻選取)，分別計算出對應的最優組合和風險結果。根據表6 可知，隨著投資組合預期收益的增加，初期持有的10 只股票賣掉的比例基本上呈上升趨勢，主要用于購買收益更高的其余5 只股票。當達到最大的預期收益率11.37%時，初始的10 只股票全部賣掉，用于購買收益率更高的第11 和第14 支股票。當繼續提高組合的預期收益率時，這兩支股票仍然占據了全部的投資比重。

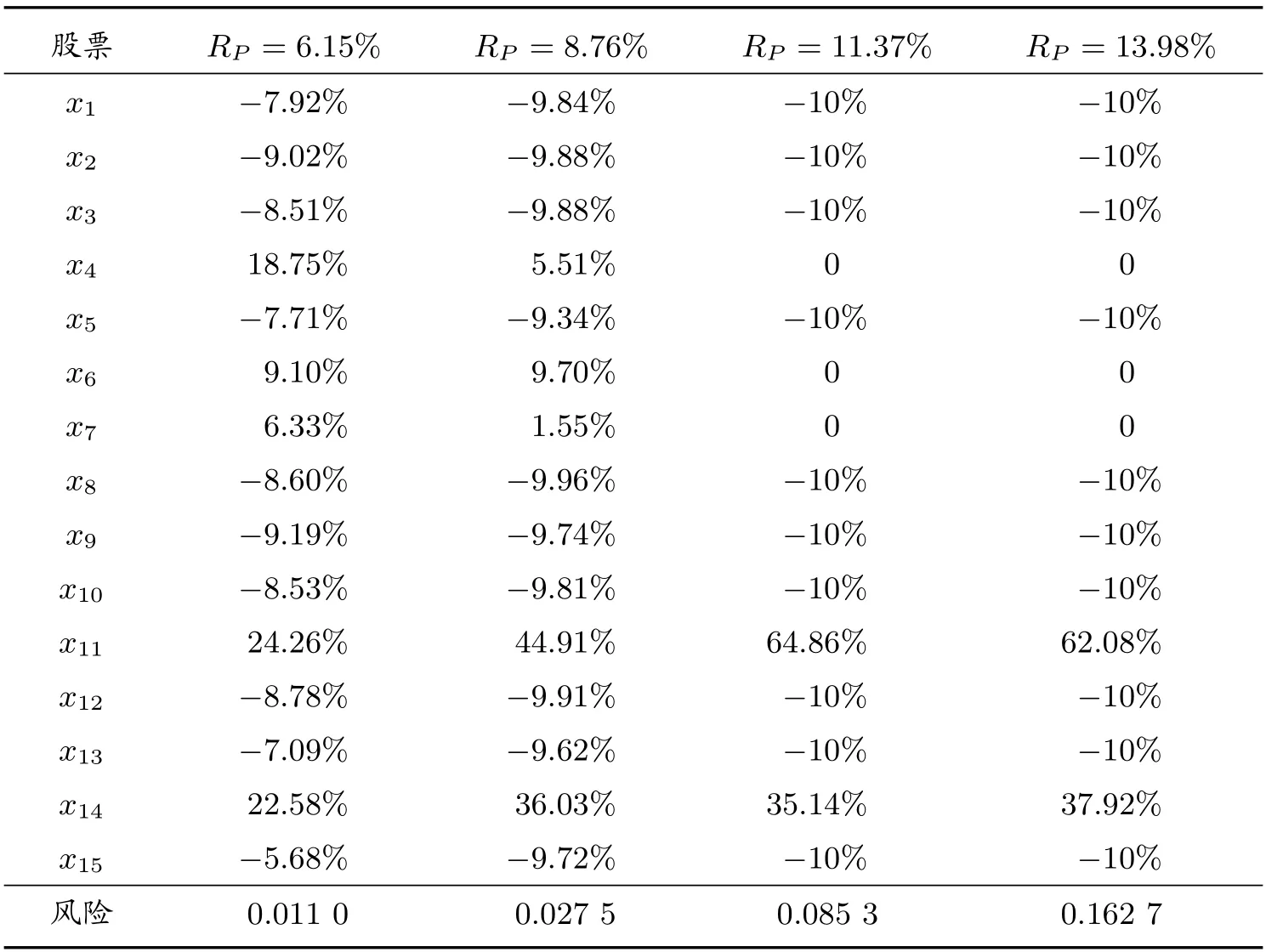
表6 投資組合模型的最優解

最后，將改進算法與差分進化算法、PSO 和QPSO 進行對比。比較實驗中，種群數均選擇3，迭代次數為1 000 次，每種算法運行30 次，計算不同預期收益率下的風險的均值和方差，結果見表7。由表7 可知，在給定預期收益率情況下，HQPSO 相比其余三種進化算法，都取得了更小的均值，同時其穩定性也更好。結果表明在給定收益的情況下，運用HQPSO 算法獲得的自融資投資組合承受較小的風險。

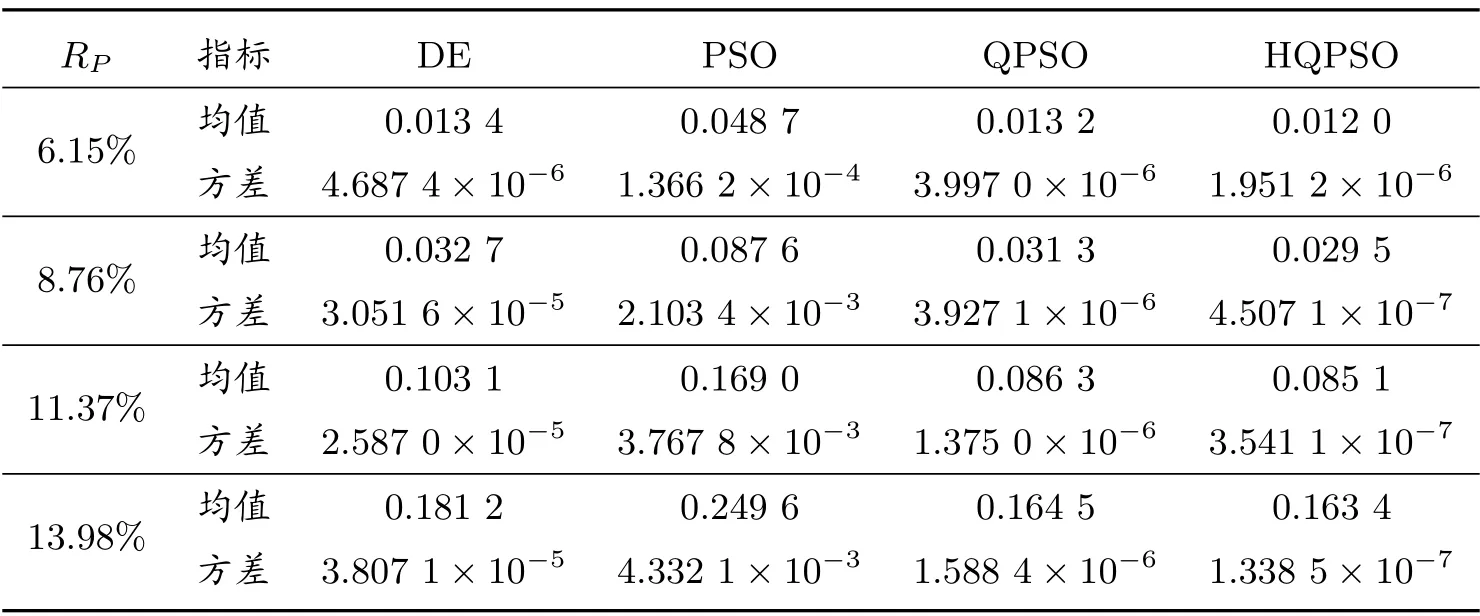
表7 不同智能算法的對比

4 結束語

為了有效地解決QPSO 算法在后期收斂速度慢以及易陷入局部最優的問題，提出了一種改進的量子粒子群群優化算法。在改進算法中，將L′evy 飛行策略引入到粒子迭代公式中，增強了粒子的局部探索精度和全局搜索速度。同時在算法中考慮了混合概率分布，在保證種群多樣性的情況下，避免算法過早陷入局部最優。通過算法對比分析，HQPSO 算法在一系列測試函數中展現出更好的收斂精度和魯棒性。在算法應用實例中，運用HQPSO 求解一類自融資投資組合問題，相比幾種經典的智能算法，改進算法在尋優的精度和穩定性上表現更好。如何進一步提高算法的收斂速度和精度，以及在更多領域中的應用，是今后研究中需要考慮的問題。