基于憶阻器的隨機(jī)神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性

王 芬

(廣東金融學(xué)院金融數(shù)學(xué)與統(tǒng)計學(xué)院，廣州 510521)

0 引言

人工神經(jīng)網(wǎng)絡(luò)是模擬生物神經(jīng)系統(tǒng)的組織結(jié)構(gòu)和系統(tǒng)功能的高度復(fù)雜的非線性動力系統(tǒng)，其中突觸是神經(jīng)網(wǎng)絡(luò)中神經(jīng)元信號的傳輸通道，也是人類大腦學(xué)習(xí)和記憶的基本組成單位，合理的突觸仿生是實現(xiàn)神經(jīng)形態(tài)計算的重要基礎(chǔ)[1–2]。在傳統(tǒng)的神經(jīng)網(wǎng)絡(luò)中，一般使用集成電路對突觸進(jìn)行模擬。1971 年，美國學(xué)者Chua 基于電路理論的完備性提出了憶阻器的概念[3]，稱其為第四種基本電路元件。2008 年，Strukov 等制造出了固體憶阻，并把他們的結(jié)果發(fā)表在Nature 雜志上[4]。憶阻器是一種具有“記憶”功能的納米級的天然非線性電阻，其阻值能夠跟隨流過器件本身的電流的變化而改變，并存儲電流斷開時的電阻值。憶阻器同時具備低功耗、學(xué)習(xí)和存儲功能，給人工神經(jīng)網(wǎng)絡(luò)中高密度的突觸模擬提供了一種極好的選擇[5]。目前，憶阻神經(jīng)網(wǎng)絡(luò)已經(jīng)在模式識別、智能計算、大數(shù)據(jù)分析、信號處理和圖像處理等方面表現(xiàn)出了良好的應(yīng)用潛質(zhì)。

迄今為止，針對憶阻神經(jīng)網(wǎng)絡(luò)的動力學(xué)行為及其控制的討論還處于起步階段，研究焦點之一是針對憶阻神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性、同步控制等內(nèi)容的分析[6–11]。

另一方面，按照生理學(xué)的觀點，生物神經(jīng)元本質(zhì)上是隨機(jī)的。然而，在隨機(jī)干擾的情況下，神經(jīng)網(wǎng)絡(luò)的動力學(xué)行為變得異常復(fù)雜[12–25]。

2019 年，基于不動點定理和激活函數(shù)的幾何性質(zhì)，研究者分析了基于憶阻器的模糊神經(jīng)網(wǎng)絡(luò)的多穩(wěn)定性和多周期性問題[10]。2017 年，Jiang 等利用Lyapunov 泛函法、拓?fù)涠壤碚摚芯苛司哂行孤稌r滯的憶阻神經(jīng)網(wǎng)絡(luò)周期解的全局指數(shù)穩(wěn)定性[11]。2017 年，Rao 等獲取了具有馬爾科夫跳變的脈沖BAM 神經(jīng)網(wǎng)絡(luò)的隨機(jī)穩(wěn)定性的LMI 判別條件[18]。遺憾的是，目前針對基于憶阻器的隨機(jī)神經(jīng)網(wǎng)絡(luò)的研究并不多見。怎樣在隨機(jī)擾動的環(huán)境下研究基于憶阻器的神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性，成為了擺在廣大研究者面前的重要課題。

綜上所述，本文將通過構(gòu)造合適的Lyapunov 泛函，應(yīng)用It?o 微分公式、微分包含和集值映射理論等，以基于憶阻器的隨機(jī)神經(jīng)網(wǎng)絡(luò)為研究對象，分析確保該系統(tǒng)的均方指數(shù)穩(wěn)定的充分判別條件。

符號說明：R 代表實數(shù)域；Rn表示n維歐式空間；R+代表非負(fù)實數(shù)集。

1 模型與預(yù)備知識

考慮如下基于憶阻器的隨機(jī)神經(jīng)網(wǎng)絡(luò)模型

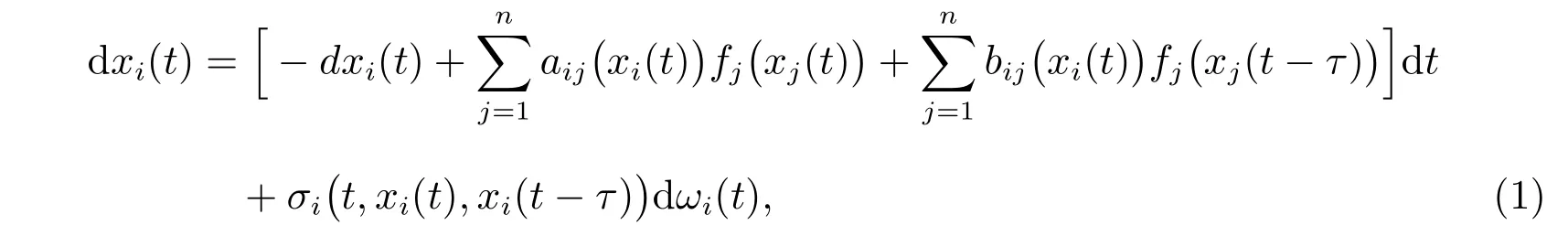
其中xi(t)為加在電容器Ci兩端的電壓；fi(xi(·))為神經(jīng)元的激勵函數(shù)；τ為離散時滯；aij(xi(t)),bij(xi(t))(i= 1,2,···,n),d> 0 表示反饋鏈接權(quán)重，其亦可以寫成如下形式

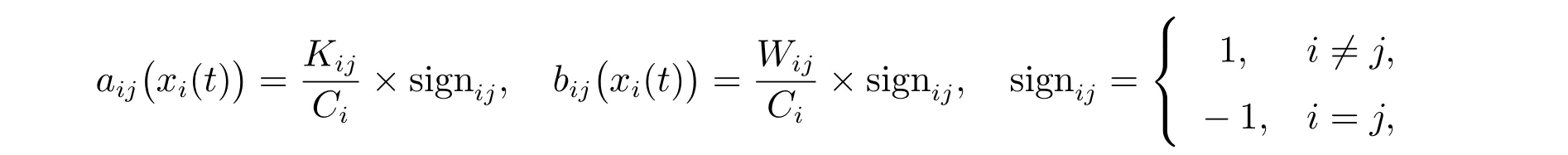
其中Kij和Wij均代表憶阻的憶感。根據(jù)憶阻的特性及其電壓與電流之間的曲線特點，為方便研究，可令

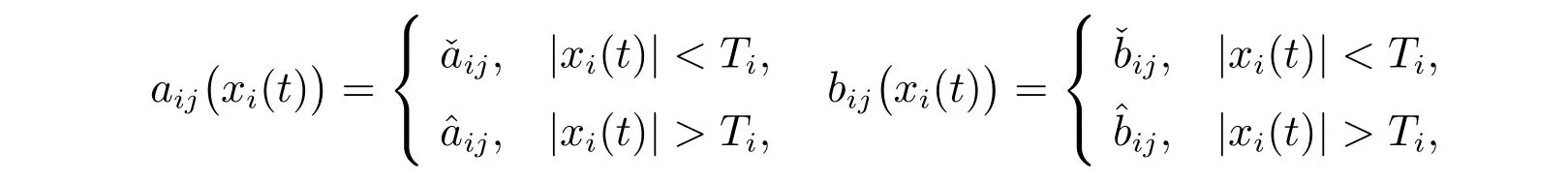
其中切換界值Ti>0(i,j=1,2,···,n)；、和都是常數(shù)。ω(t)=[ω1(t),ω2(t),···,ωn(t)]T ∈Rn是n維Brownian 運動，定義在帶有自然域流{Ft}t≥0上的完備概率空間(?,F,P)上。

系統(tǒng)(1)初始條件為x(s)=φ(s),s ∈[?τ,0]，其中x(s)=[x1(s),x2(s),···,xn(s)]T為系統(tǒng)在時刻s的狀態(tài)變量；φ(s)=[φ1(s),φ2(s),···,φn(s)]T,φi(s)是有界連續(xù)函數(shù)。

本文中所有系統(tǒng)的解都是在Filippov 的意義下，在這里

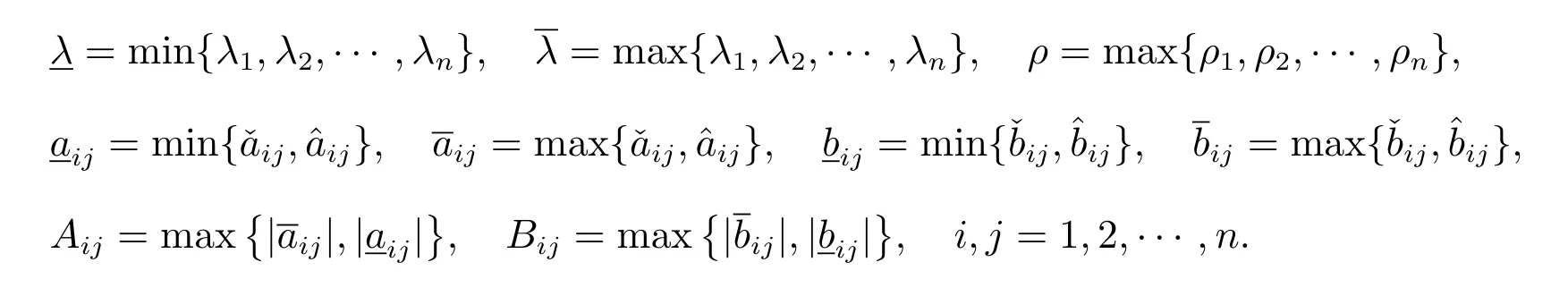
通過微分包含和集值映射理論，系統(tǒng)(1)可以描述為

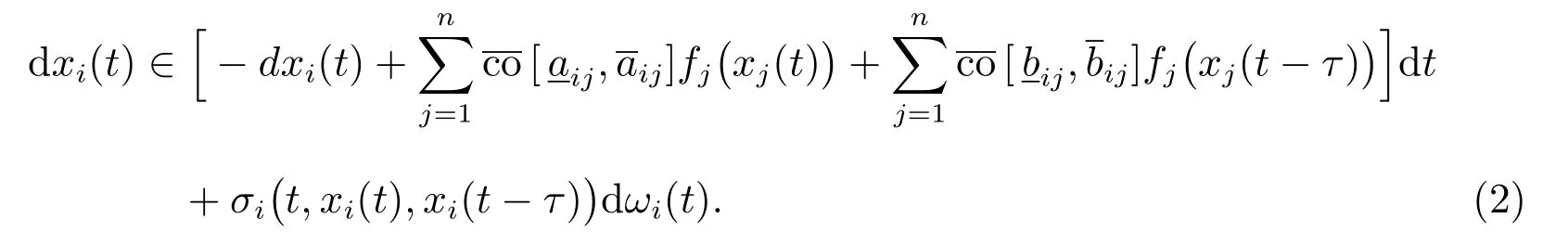
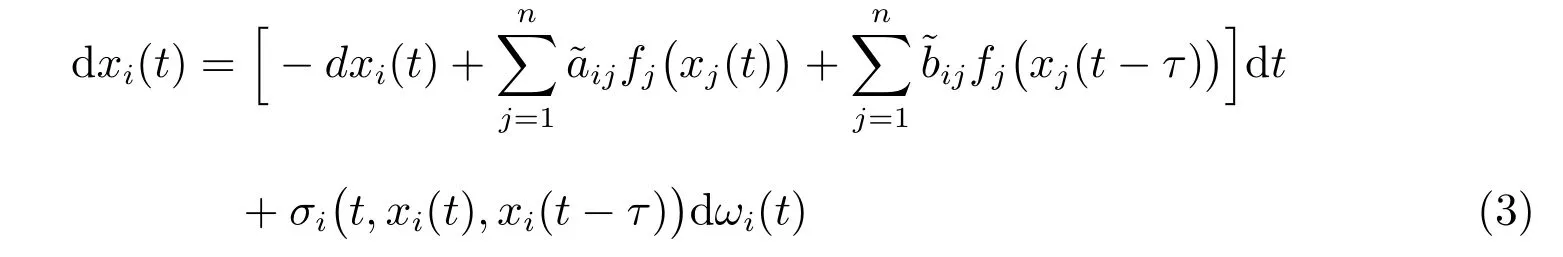
成立。

若不考慮隨機(jī)擾動的影響，則系統(tǒng)(1)可以簡化為

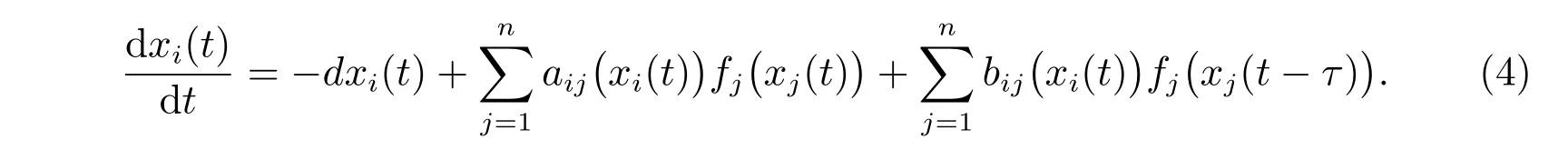
為了獲得主要結(jié)果，接下來給出如下定義和假設(shè)。

定義1[25]如果存在正數(shù)K>1 和α>0，使得系統(tǒng)(1)的解滿足

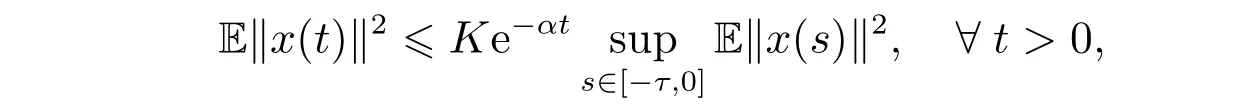
則稱系統(tǒng)(1)的平衡解均方指數(shù)穩(wěn)定。

定義2[26]如果存在正數(shù)β>1 和α>0，使得系統(tǒng)(4)的解滿足

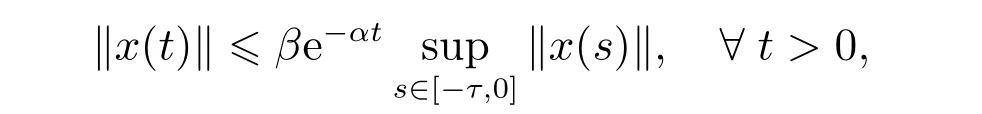
則稱系統(tǒng)(4)的解全局指數(shù)穩(wěn)定。

引理1(公式)[27]令u=u(t,x1,x2,···,xn)T是定義在[t0,T]×Rn上的連續(xù)函數(shù)且存在連續(xù)偏導(dǎo)數(shù)ut、uxi、uxixj(i,j=1,2,···,n)。若n維隨機(jī)過程x(t)=[x1(t),x2(t),···,xn(t)]T在[t0,T]滿足

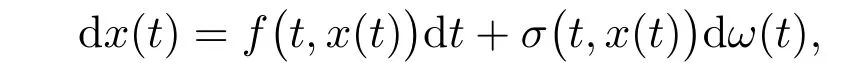
則隨機(jī)過程V(t,x(t))=u(t,x1,x2,···,xn)T的隨機(jī)微分為

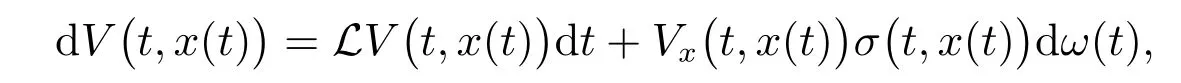
其中

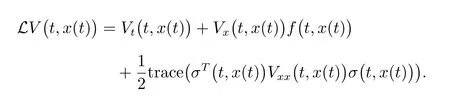
假設(shè)1激勵函數(shù)fi(·)滿足fi: R→R,fi(0) = 0。同時，存在正數(shù)Fi，使得對于任意ξ ?=0,ξ ∈R，不等式

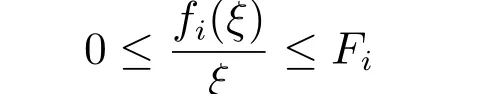
成立，其中i=1,2,···,n。

假設(shè)2σi: R+×R×R→R 滿足局部Lipschitz 連續(xù)性，并且σi(t,0,0) = 0。同時，存在非負(fù)實數(shù)ui和vi，使得不等式

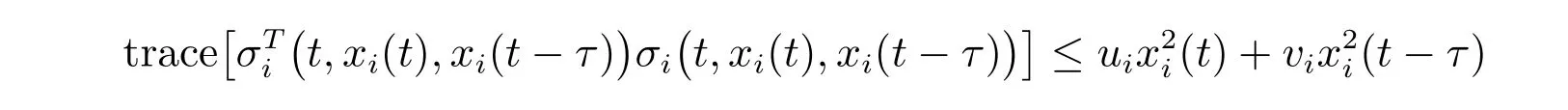
成立，其中i=1,2,···,n。

2 主要結(jié)論

定理1若系統(tǒng)(1)滿足假設(shè)1 和假設(shè)2，且存在正數(shù)ε、λi、ρi(i= 1,2,···,n)，使得下列的不等式組

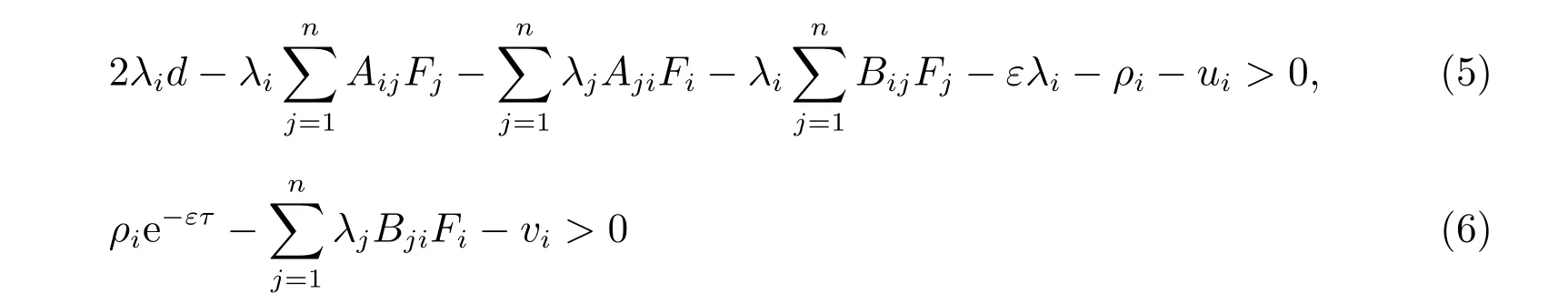
成立，則系統(tǒng)(1)均方指數(shù)穩(wěn)定。

證明 構(gòu)造如下正定的Lyapunov 泛函

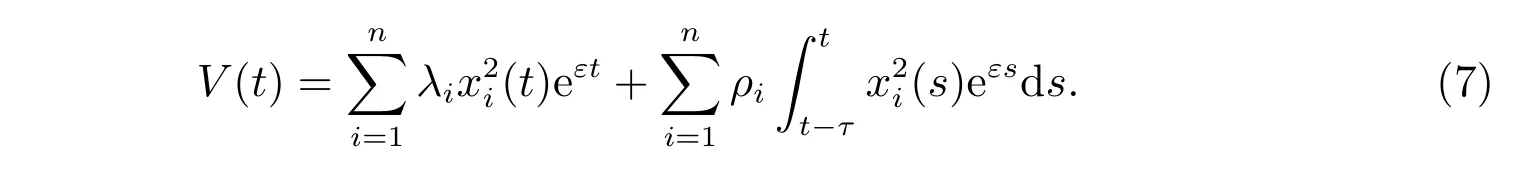
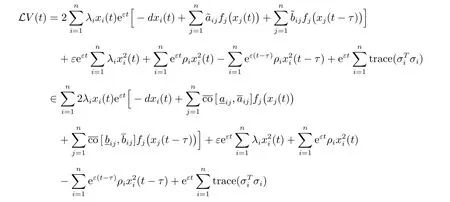
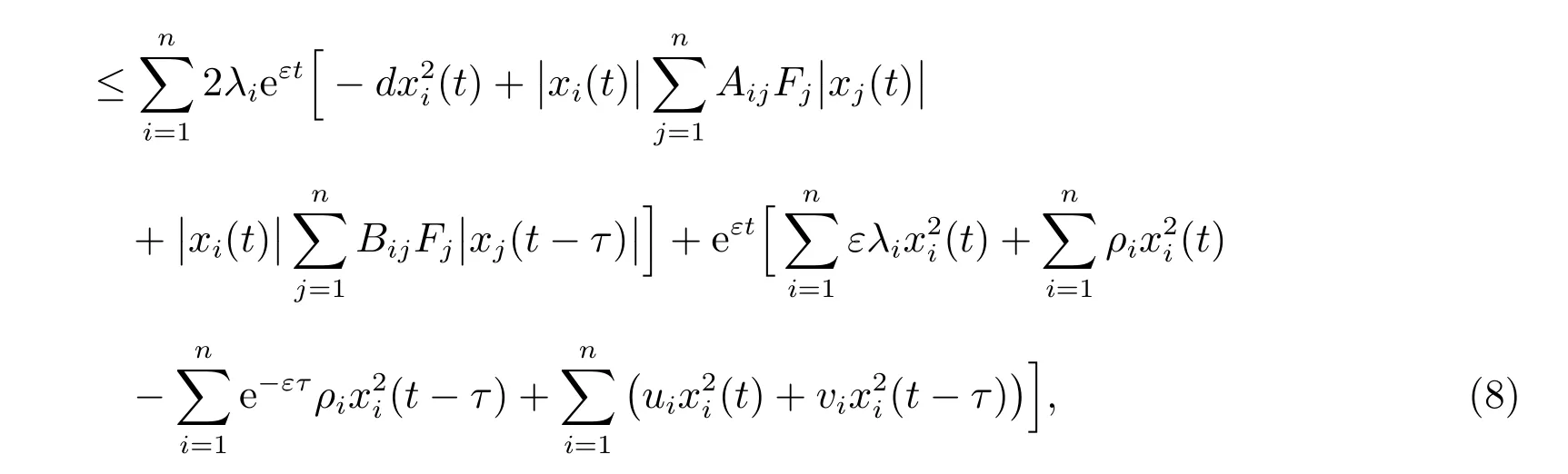
其中

將(9)式和(10)式代入(8)式，可得

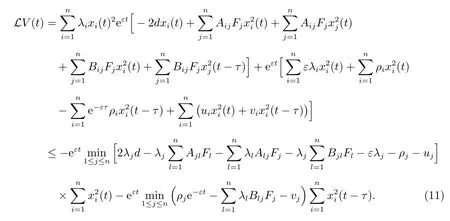
若存在正實數(shù)ε、λi、ρi(i=1,2,···,n)，使得下列不等式

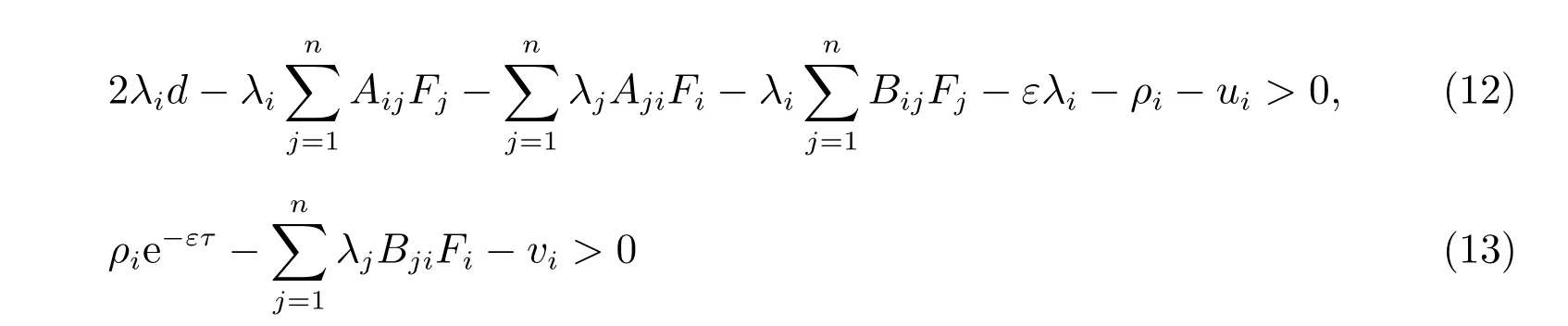
成立，則LV(t)≤0。進(jìn)一步，可得

同時，可以知道

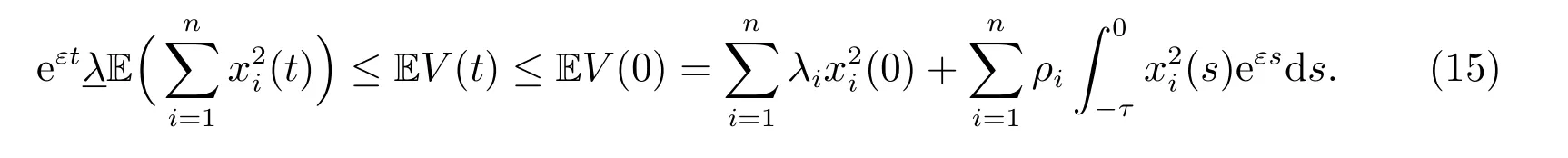
因而，可得

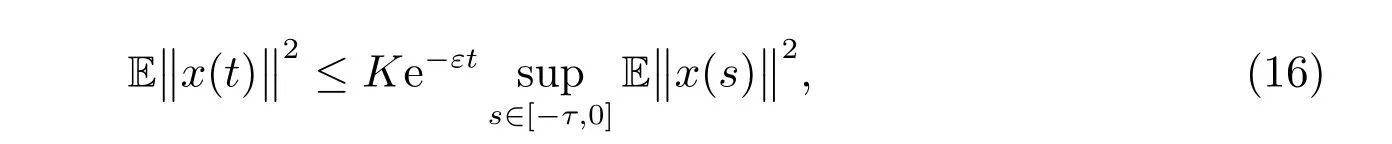
注1在文獻(xiàn)[28]中，研究者利用微分包含理論，研究了憶阻遞歸神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性問題。然而，文獻(xiàn)[28]并沒有考慮隨機(jī)擾動的影響。本文在隨機(jī)擾動的環(huán)境下，利用It?o 微分公式、微分包含，綜合考慮了基于憶阻器的神經(jīng)網(wǎng)絡(luò)的均方指數(shù)穩(wěn)定性問題。因而，較文獻(xiàn)[28]有更加廣泛的適用范圍。

注2在文獻(xiàn)[29]中，基于It?o 微分公式、Lyapunov-Krasovskii 泛函，研究者獲得了用線性矩陣不等式表示的具有漏泄時滯的隨機(jī)神經(jīng)網(wǎng)絡(luò)指數(shù)穩(wěn)定的充分條件。然而，文獻(xiàn)[29]并沒有在基于憶阻器的前提下展開研究。本文結(jié)合憶阻器在突觸模擬中的明顯優(yōu)勢，使用憶阻器模擬突觸。因而，本文的結(jié)論為神經(jīng)網(wǎng)絡(luò)在設(shè)計過程中高密度突觸的選擇提供了更加寬廣的理論基礎(chǔ)。

接下來，研究不具有隨機(jī)項的憶阻神經(jīng)網(wǎng)絡(luò)系統(tǒng)(4)的穩(wěn)定性，可以用類似定理1 的證明方法，得到下述推論。

推論1若系統(tǒng)(4)滿足假設(shè)1，且存在正數(shù)ε、λi、ρi(i= 1,2,···,n)，使得下列的不等式組成立，則系統(tǒng)(4)全局指數(shù)穩(wěn)定。

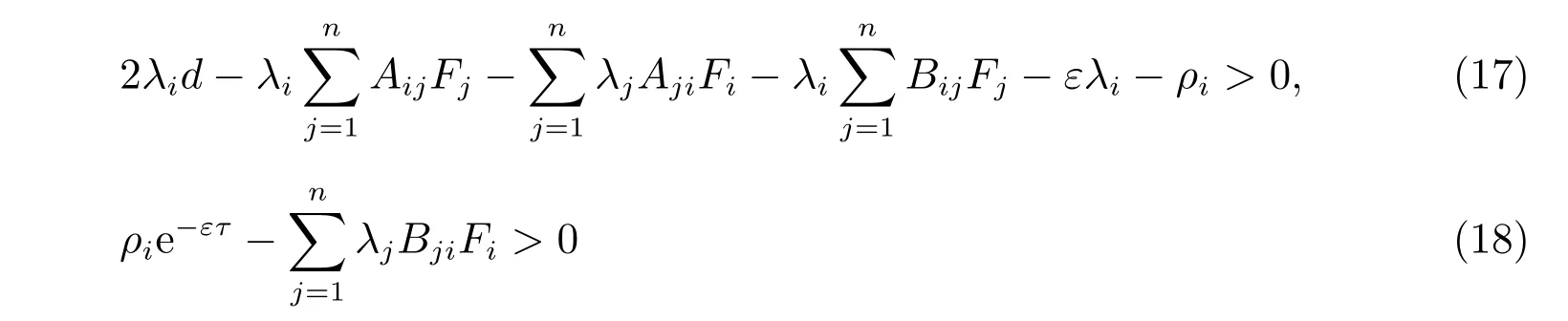
注3可以考慮在系統(tǒng)(1)中加入脈沖因子，依據(jù)類似于定理1 的分析方法，研究基于憶阻器的隨機(jī)脈沖神經(jīng)網(wǎng)絡(luò)的均方指數(shù)穩(wěn)定性，更深層次地展開針對隨機(jī)憶阻神經(jīng)網(wǎng)絡(luò)的研究。

3 數(shù)值仿真

例1考慮如下的基于憶阻器的隨機(jī)神經(jīng)網(wǎng)絡(luò)

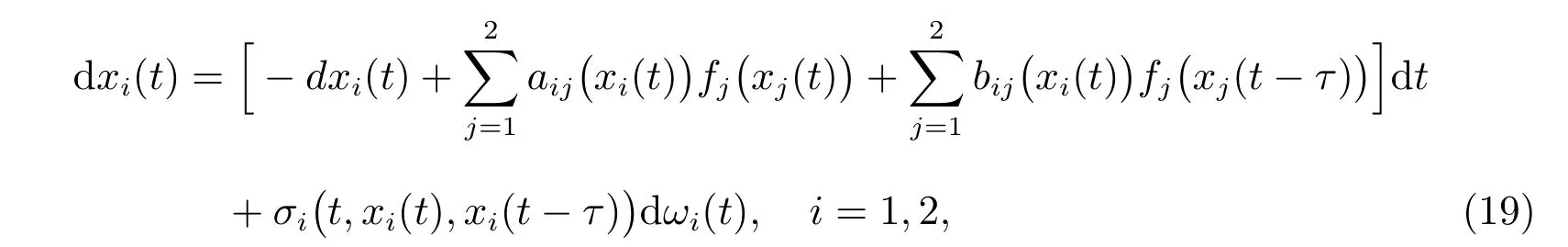
其中

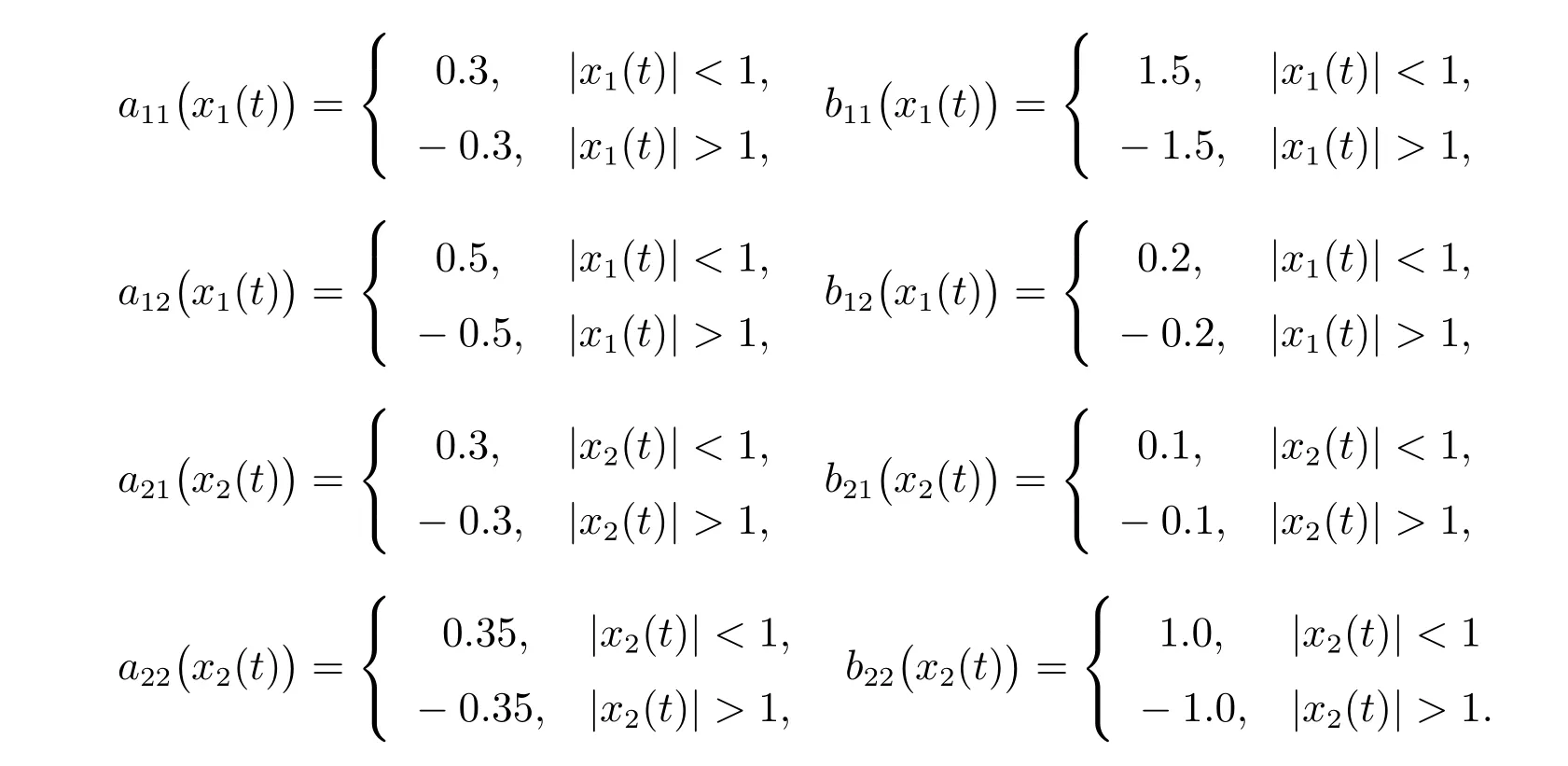
再由

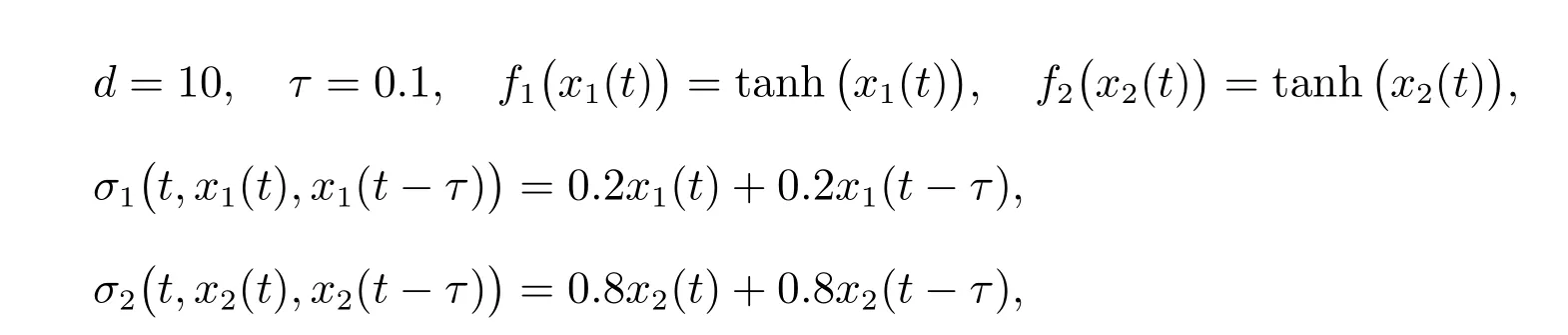
易知

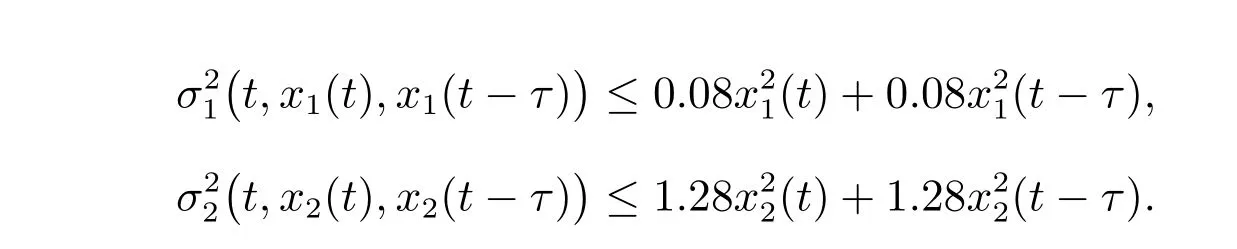
取λ1=λ2=2,ρ1=ρ2=10,ε=1，經(jīng)過簡單的計算可得

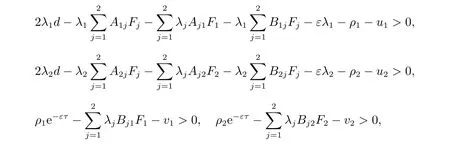
則由定理1 可得，系統(tǒng)(19)均方指數(shù)穩(wěn)定。取系統(tǒng)的初始條件為x1(t) = 50,x2(t) =?20，經(jīng)過Matlab 仿真可以得到系統(tǒng)(19)中的x(t)的狀態(tài)曲線，如圖1 所示。

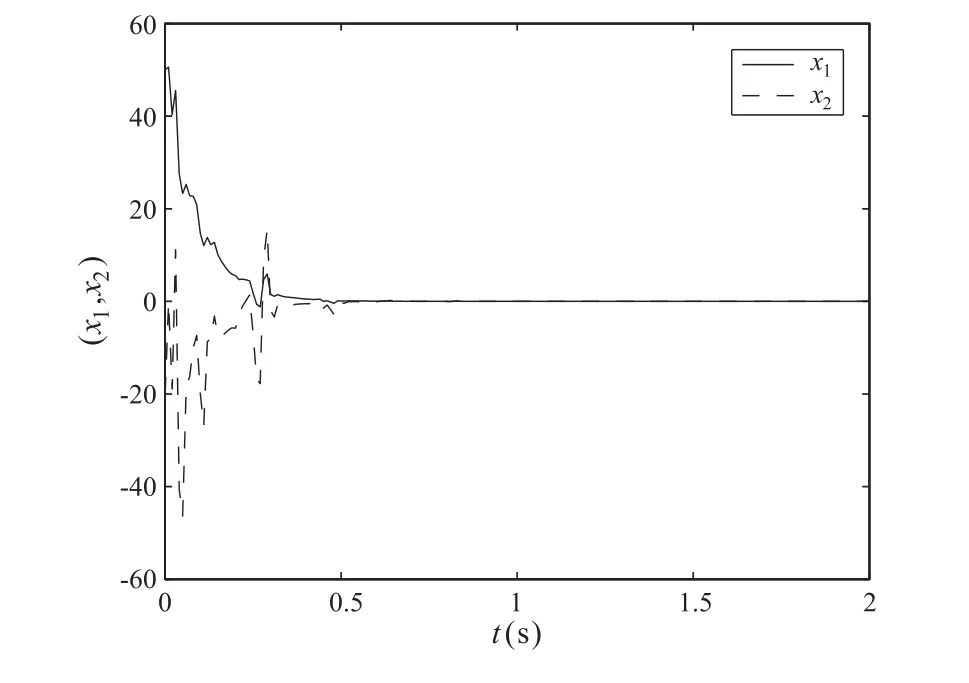
圖1 系統(tǒng)(19)中的x(t)的狀態(tài)曲線圖

例2考慮如下的基于憶阻器的神經(jīng)網(wǎng)絡(luò)

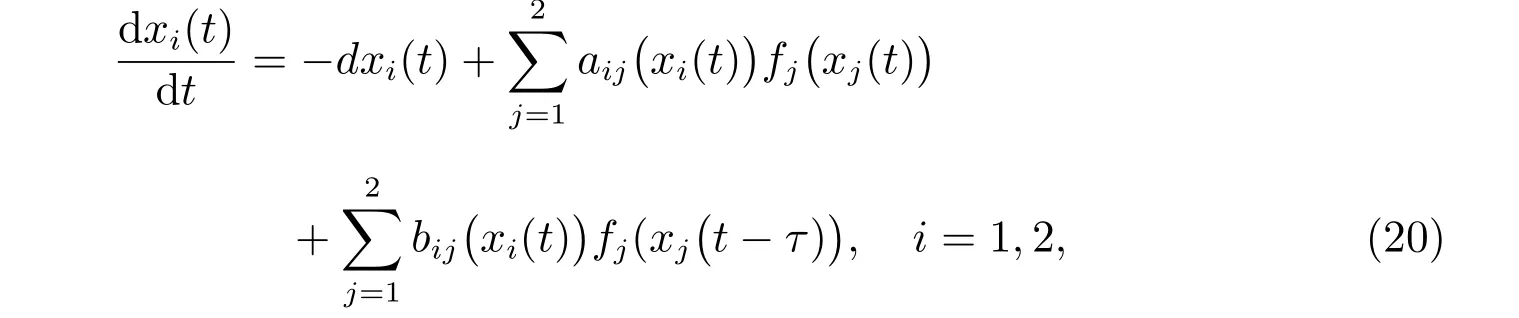
其中

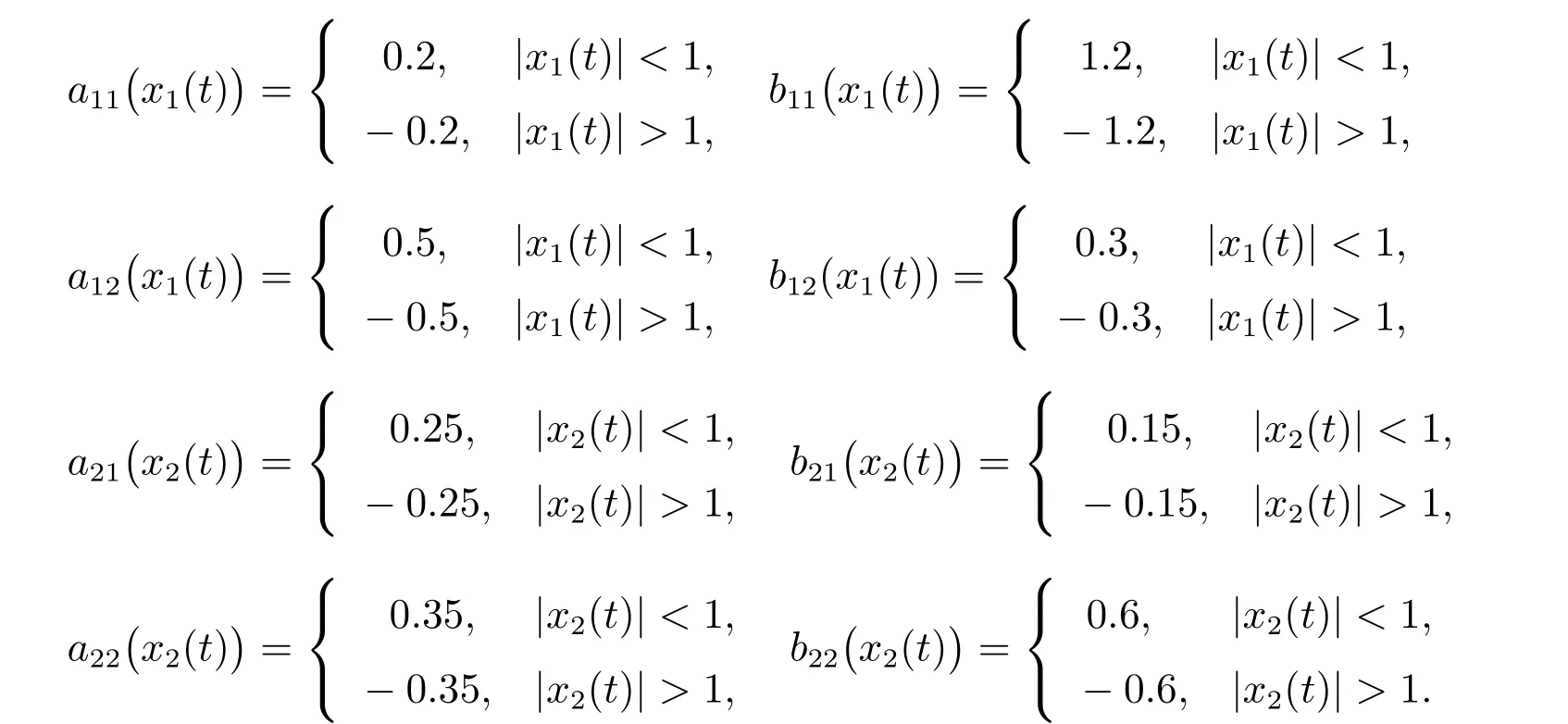
另有

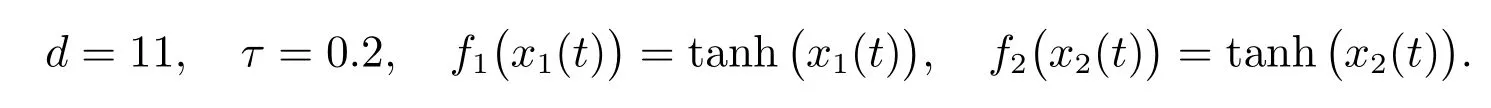
取λ1=λ2=2.5,ρ1=ρ2=10,ε=1，經(jīng)過簡單的計算可得

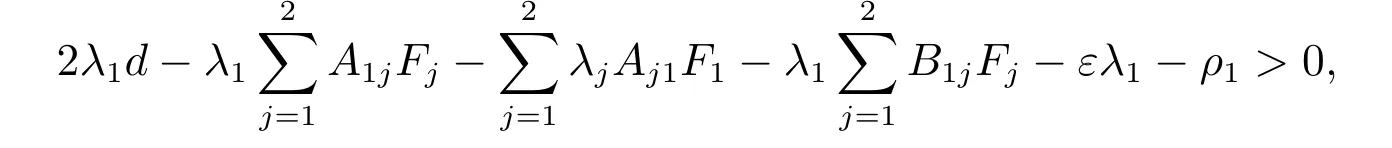
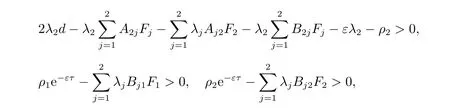
則由推論1 可得，系統(tǒng)(20)全局指數(shù)穩(wěn)定。取系統(tǒng)的初始條件為x1(t) =?35,x2(t) =35，經(jīng)過Matlab 仿真可以得到系統(tǒng)(20)中的x(t)的狀態(tài)曲線，如圖2 所示。

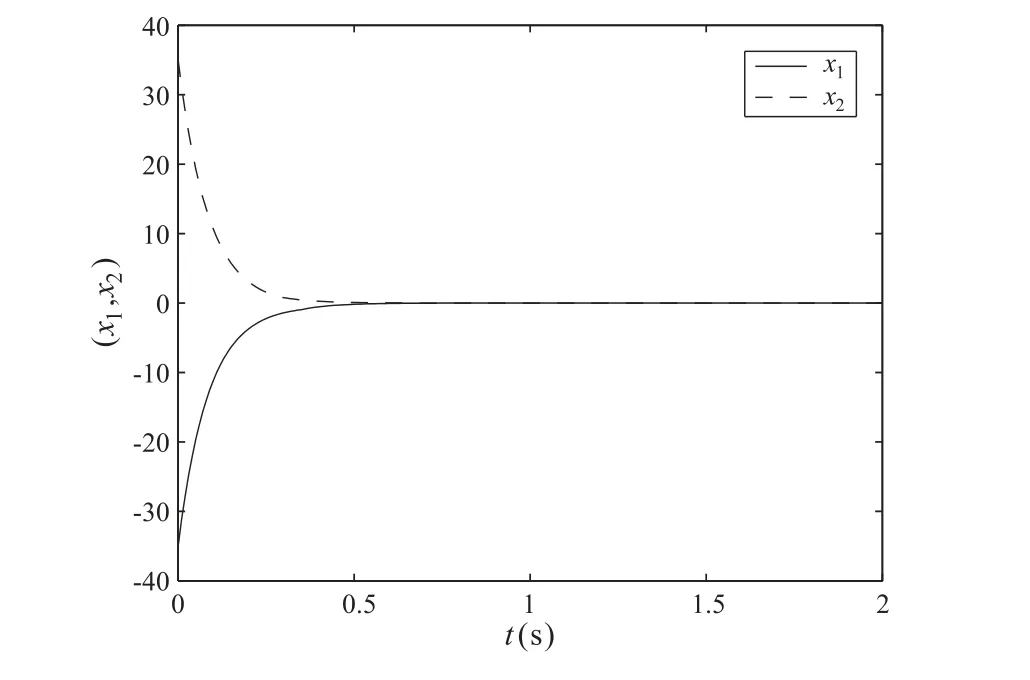
圖2 系統(tǒng)(20)中的x(t)的狀態(tài)曲線圖

4 結(jié)論

本文以隨機(jī)擾動下的憶阻神經(jīng)網(wǎng)絡(luò)為研究對象，應(yīng)用Lyapunov 泛函、It?o 微分公式和不等式技巧，得到了該系統(tǒng)均方指數(shù)穩(wěn)定的充分判別條件。最后，通過兩個仿真例子，說明了所得結(jié)論的有效性。