動態(tài)規(guī)劃及其算法應用

文超婷 沈秋銘 姚仁杰 李雙喜

牡丹江師范學院計算機與信息技術學院 黑龍江牡丹江 157011

1 概述

動態(tài)規(guī)劃類似于分治法。將一些待解決的問題全部分割為一個一個的小問題分別解決，一般情況下，動態(tài)規(guī)劃函數(shù)是指利用子問題的重疊關系可以得到求解問題的遞歸關系。得到遞歸關系之后，就可以利用這個關系來求解問題，這也就是動態(tài)規(guī)劃函數(shù)。采用動態(tài)規(guī)劃算法將子問題的解通過分析表格數(shù)據(jù)存儲下來，相較于分治法處理獨立子問題而言，記憶化搜索可以有效地解決分治法中重復求解子問題的效率問題。

2 動態(tài)規(guī)劃求解過程

動態(tài)規(guī)劃的本質是對問題進行定義之后建立狀態(tài)轉移的方程。我們可以將動態(tài)規(guī)劃的理論理解為將想要探究的問題劃分成若干個小的子問題，這些子問題都有相應的解。在這些可行的解決方案中，必須有一個最優(yōu)的解決方案。

如何合理地推導出求解最優(yōu)值的方程，正確地找到臨界值，是進行動態(tài)規(guī)劃方法過程中的基本的要求。基于此，研究某個問題時先要把研究對象劃分為N個密不可分的子對象，推算出其中的各個重要變量和最優(yōu)值方程式，這樣就把研究對象劃分為N個子對象，一一推導尋求出結果。每一個臨界條件，都有一個臨界值，再一次求解，這樣在每一個子過程求解中都可以找到最優(yōu)化的結果，這樣重復操作，就可以得到最后一個方程的結果，并且也可以得到研究對象的最佳計算結果。

對多個子對象的研究過程中，通常動態(tài)規(guī)劃方法不同于當前對象和未來子對象，然而綜合考慮當前和未來是解決最優(yōu)化的關鍵所在，每個子對象的研究結果都要綜合全局考慮，又不同于每個子對象的最優(yōu)研究結果。

在求解研究對象的最佳解決方案的時候，初始條件已知，每個子對象的結果都是該子對象的狀態(tài)函數(shù)，因此最優(yōu)解也是通過各個子對象的各個狀態(tài)一一變換時所得到的。

動態(tài)規(guī)劃算法是否有效主要取決于下述的兩個方面，首先，是子問題的最佳結構，其次，是子問題是否具有重疊性。

(1)最優(yōu)子結構：當該問題的最佳解決方案包括了下層子問題的最優(yōu)解的時候，可以說該子結構具有良好的性質。

(2)重疊子問題：當使用自頂向下的遞歸方法解決問題時，使用的每一個子問題都不一定是新產(chǎn)生的，有的時候，我們需要反復多次的計算其中的一部分子問題。在動態(tài)規(guī)劃方法中，每個子問題只能求解一次，但由于子問題是重疊的，所有子問題都可以存在于表中，未來我們解決問題的同時可以盡可能多地使用這些子問題的解。

實現(xiàn)動態(tài)規(guī)劃算法一般可以分為自頂向下遞歸或者自底向上遞推的方法。

自頂向下是指，先劃分整個數(shù)組，然后再劃分子數(shù)組，直到我們所有子數(shù)組只包含一個重要元素，然后逐層合并。因此，最好使用遞歸來實現(xiàn)這一點。

自底而上是指，對整個陣列世界進行合并，可以合并相鄰的兩個元素，然后再對相鄰的四個元素進行合并，直到將所有的數(shù)組都合并了之后，可以完成排序。

在使用動態(tài)規(guī)劃來處理這個問題時，我們首先需要得到最佳解決方案的基本性質，找到其基本的結構，然后可以使用上文中的遞歸的方法來找到最佳的計算結果。將問題進行細化分解后，再把每一個子問題得到的最優(yōu)值的有效信息通過表格形式存放，最后利用問題之間的重疊聯(lián)系得到解決問題的方程組，以獲得最優(yōu)解的具體結果。

3 應用分析

3.1 最長公共子序列(Longest Common Subsequence)

問題描述。給兩個字符串S1以及S2，求子序列在S1中且子序列也在S2中的字符串，所得的字符串的最大長度為多少。

首先定義子問題，設F(i，j)表示序列S1={x1，x2，…xn}和序列S2={y1，y2…ym}表示為最長公共子序列的長度，那么初始的子問題為序列S1和S2至少有一個空序列，因此S1和S2與空序列之間的最長公共子序列均為0，即F(i，0)=F(j，0)=F(0，0)=0。

根據(jù)圖1關于字符串a(chǎn)sdfgh以及字符串a(chǎn)dsdg的狀態(tài)矩陣，使用F[i][j]表示字符串前i個字符以及前j個字符的最長公共子序列長度。

該題目對于集合的劃分有四種情況。

(1)S1[i]不在集合中，S2[j]也不在集合中。

(2)S1[i]不在集合中，S2[j]在集合中。maxlength=F[i-1][j]，由于F[i-1][j]表示在S1和S2中前i-1個字符以及前j個字符出現(xiàn)，但是S2[j]不一定會在F[i-1][j]的集合中出現(xiàn)，與條件中的S1[i]不在集合中，S2[j]在集合中不符，但是在動態(tài)規(guī)劃函數(shù)中，依然可以用F[i-1][j]來表示，因為這個條件是F[i-1][j]的一個子集，而我們所需要獲取的是maxlength，所以使用F[i-1][j]對maxlength的結果并不會造成影響。

(3)S1[i]在集合中，b[j]不在集合中。原理同(2)，采用F[i][j-1]表示。

(4)S2[i]在集合中，b[j]也在集合中。則maxlength=F[i-1][j-1]+1。

在實際計算中，情況(1)被包含在情況(2)(3)，因此只需要將問題劃分為兩種可能。

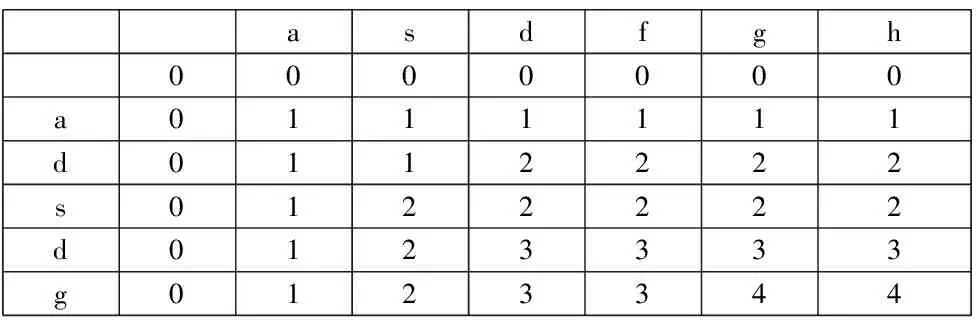
字符串a(chǎn)sdfgh與字符串a(chǎn)dsdg的狀態(tài)矩陣表

則有如下動態(tài)規(guī)劃函數(shù)：

對于該問題給出以下算法：

void LCS()

{

cin>>n>>m；

cin>>a+1>>b+1；

for(int i=1；i<=n；i++)

for(int j=1；j<=m；j++)

{

F[i][j]=max(F[i-1][j]，F(xiàn)[i][j-1])；//②和③的情況一定存在，所以可以無條件優(yōu)先判斷

if(a[i]==b[j])F[i][j]=max(F[i][j]，F(xiàn)[i-1][j-1]+1)；

}

cout<

}

3.2 0-1背包問題

問題描述。假設有一個背包，里面有很多東西，并且東西都有一定的價值。如果數(shù)量為n，且每件物品只能裝入背包一次，在不超過背包容量的情況下，這個背包可以裝入的總價值是多少？

我們將前i個物品，背包容量為j的最優(yōu)解的狀態(tài)設為F(i，j)，Capacity[i]為第i個物品所需的背包容量，第i個物品的價值由Value[i]來表示，目前的狀態(tài)的最優(yōu)解與前一個的狀態(tài)的最優(yōu)解有關，處于依賴關系，將F(0，0)設為初始狀態(tài)，也就是第0個物品裝入背包容量j=0的狀態(tài)下F(0，0)=0，當我們將第0個物品裝入背包容量j大于或者等于0或者前i個物品裝入背包容量j為0時的情況下狀態(tài)F(i，j)=0，由此可得F(0，j)=F(i，0)=0。由此可得背包容量比物品的重量小，j<第i個物品所需容量，即Capacity[i]，則第i個物品不能裝入背包內，因此前i個物品能裝入背包的價值最優(yōu)解也就是前i-1個物品能裝入背包的價值最優(yōu)解，由此可得F[i][j]=F[i-1][j]。

當背包容量足以放入第i個物品，也就是j>Capacity[i]，那么我們需要做出選擇，是否把第i個物品也放在里面。如果選擇裝入可得方程為：F[i][j]=F[i-1][j-Capacity[i]]+Value[i]；不裝入的話可以得到，F(xiàn)[i][j]=F[i-1][j]，最后為了得到選與不選的最優(yōu)解，需要對兩種情況進行比較，得到的最大值max則為當前狀態(tài)下的最優(yōu)解。則有如下動態(tài)規(guī)劃函數(shù)：

對于該問題給出以下算法：

void bag()

{

int n，m；

cin>>n>>m；

for(int i=1；i <=n；i++)

cin>>Capacity[i]>>Value[i]；

for(int i=1；i<=n；i++)

for(int j=1；j<=m；j++)

{

if(j

F[i][j]=F[i-1][j]；

else

F[i][j]=max(F[i-1][j]，F(xiàn)[i-1][j-Capacity[i]]+Value[i])；

}

cout<

}

根據(jù)以上分析，可以優(yōu)化為一維動態(tài)規(guī)劃求解。

首先，我們需要明確為什么可以簡化二維的動態(tài)規(guī)劃求解的思想為一維解法，因為第i項的最優(yōu)值依賴并且只依賴于第i-1項的最優(yōu)值，也就是說無論是i-2，i-3等的最優(yōu)狀態(tài)都不需要被第i項的求解使用。在背包問題上，每一個物品結束選擇之后，該物品的體積和價值對于之后的最優(yōu)值計算不會被利用，因此我們將二維壓縮為一維即可以有效節(jié)省空間復雜度。

其次，我們需要了解當二維被簡化，用一維解題時，為什么需要用逆序的方式來更新當前背包的容量的最優(yōu)結果，也就是j從Capacity開始向下更新。在我們對F一維數(shù)組進行更新時，只有上一層的F數(shù)組中的數(shù)值，因此在更新下標較大的數(shù)組數(shù)值時，其上一層的F數(shù)組數(shù)值保持原始值，沒被更新。所以在進行背包問題的最優(yōu)問題簡化到一維求解，我們需要將其的索引值從背包的總容量逐步減小進行更新。

定義狀態(tài)F[j]在背包容量為j的情況下，裝有N件物品的最優(yōu)解，由于采用一維解法，所以利用逆向思維將背包容量j從背包的最大容量開始枚舉。由此得到狀態(tài)轉移方程為F[j]=max(F[j]，F(xiàn)[j-Capacity[i]]+Value[i])。

對于該問題給出以下算法：

void bag_plus()

{

int n，m；

cin>>n>>m；

for(int i=1；i<=n；i++)

{

int Capacity，Value；

cin>>Capacity>>Value；

for(int j=m；j>=Capacity；j--)

F[j]=max(F[j]，F(xiàn)[j-Capacity]+Value)；

}

cout<

}

結語

采用動態(tài)規(guī)劃算法以最長子序列和背包問題為切入點進行研究，探究求得最優(yōu)解的方法，在最長子序列和背包問題中通過比較兩種情況(b[j]不在集合中/是否裝入第i個物品)分別分析兩種情況的結果，得出動態(tài)規(guī)劃函數(shù)，然后給出對應算法。動態(tài)規(guī)劃算法無論是在日常生活還是在程序設計實訓和競賽中，都有著顯著的算法地位并且被廣泛使用。本研究的結果意味著當解決相關的最優(yōu)解問題時，采用動態(tài)規(guī)劃算法可以有效地對時間復雜度和空間復雜度進行優(yōu)化和減少。后續(xù)研究中，將繼續(xù)尋找優(yōu)化最優(yōu)解問題的其他思想。