對稱空間濾波器組自匹配的波束形成算法*

楊 燁，秦 云

（江蘇大學，江蘇 鎮江 212013）

0 引言

陣列信號處理就是通過對傳感器進行特定的排列來采集空間中不同的信號，并對采集到的信號進行處理的技術。在此基礎上，對采集接收到的信號和空間中存在的干擾進行特定的處理，來獲得對期望信號的最優接收的技術就是自適應波束形成技術[1]。自適應波束形成技術廣泛應用于雷達、通信、電子對抗、射電天文[2-4]等領域，是陣列信號處理技術發展所帶來的產物。自適應波束形成技術可以定向地接收空間中特定方向的信號，并且對其他方向上的干擾信號進行抑制，避免干擾信號對系統造成影響[5]。該技術實現這一功能的核心就在于對陣列天線的權值進行合理的設置，并根據環境的變化自適應地改變各陣元對應的權值，這樣一來，陣列輸出選擇一個合適的權值進行補償傳播延時，以此獲得期望方向上陣列輸出的同向疊加，并且抑制其他方向上的干擾來波，實現對各來波方向信號的增強或者抑制，獲得最優的陣列輸出[6]。自適應波束形成算法就是通過獲取各個陣元權值，實現在某種最優準則下的權集尋優[7]的算法。各個換能器陣列加權的權值系數組成的向量就是最優權矢量，通過最優權矢量的處理可以獲得陣列方向圖[8]。陣列方向圖存在一個主瓣和多個旁瓣，方向圖的主瓣決定了陣列的分辨率[9-10]。陣列分辨率的高低決定了陣列對空間信號的區分能力的高低，所以陣列方向圖主瓣越窄，算法的性能越好。

為了獲得更佳的性能，許多基于傳統波束形成算法的延伸算法被提出，如文獻[11]提出的一種變步長的約束穩定性最小均方（Constraint Stability LMS，CS-LMS）算法，在噪聲環境下能夠降低誤差，提高算法的穩定性，有效濾除噪聲對系統的影響；文獻[12]將加載因子的選擇與信號協方差矩陣的特征值掛鉤，由特征值的特點來決定對角加載因子，加強了算法對干擾的抑制能力，而且在角度失衡的情況下也有較好的算法性能，但是加載因子的選擇存在誤差，使得系統的性能大幅度降低；文獻[13]提出了根據不同導向矢量誤差獲取對應的加載量，但是最優加載值的求解方法運算量大且收斂速度也慢。以上這些方法雖然獲得了更好的性能，但也帶來了其他問題。此外，文獻[14]提出的方法有效地提高了信噪比，在10 陣元情況下，其方向圖主瓣寬度約為0.13，旁瓣約為-8 dB；在文獻[15]提出的方法中，在10 陣元情況下，其方向圖主瓣寬度約為0.18，旁瓣寬度約為-25 dB。這兩種方法都是盡可能地提高信噪比，但是沒有突破主瓣瑞利極限。

針對無法突破主瓣瑞利極限獲得更窄主瓣和更低旁瓣這一問題，本文提出一種基于對稱空間濾波器組自匹配的方法。該方法對相控陣陣元進行偏轉調制，獲得多組輸出信號。對于主響應軸方向的波束分量，偏轉調制響應是一個左右對稱的向量，而其他波束分量的調制響應則不具備對稱特性，因此將調制響應向量反轉后進行匹配濾波，即可獲得主響應軸波束分量的強度[16]。通過該種方法可以有效地濾除干擾信號的影響，增強期望信號的增益，并獲得突破主瓣瑞利極限的陣列方向圖。此外，結合傳統的線性約束最小方差（Linearly Constrained Minimum Variance，LCMV）算法，對陣列的干擾方向進行零陷約束，從而進一步提高信噪比，獲得更優秀的性能。

1 陣列信號模型

設定空間中存在N個信號源，信號從不同方向入射到M（M＞N）元陣列上，則t時刻第（ii=1,2,…,M）個陣元接收到的信號為：

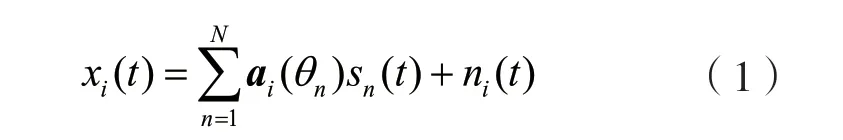
式中：sn(t)為第n個源信號；θn為第n個信號源的入射方向；ni(t)為t時刻第i個陣元接收到的高斯白噪聲；ai(θn)為信號的導向矢量，表達式為ai(θn)=e-j2πf0τin，其中τin是第n個信號源到達第i個陣元相對于參考陣元的時延，f0為期望信號的頻率。

均勻線陣所接收到的陣元數據用矩陣表示為：

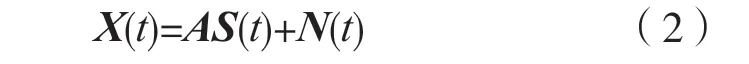
式中：陣列接收為X(t)=(x1(t),x2(t),…,xM(t))T；噪聲為N(t)=(n1(t),n2(t),…,nM(t))T；信號源復包絡為S(t)=(s0(t),s1(t),…,sN(t))T；矩陣A=(a(θ0),a(θ1),…,a(θN))是由n個導向矢量組成的，其中，a(θn)=(1,ejβl,…,ej(M-1)βl)T，βl表示第l個入射信號源入射到第二個陣元時相對于參考陣元的延遲。

2 對稱偏轉調制

本文在陣列調向的基礎上進行延伸，提出了對稱偏轉調制，即通過對換能器陣列左右進行等角度、等次數的對稱偏轉調制獲得多組陣列響應。對于主響應軸方向的波束分量，偏轉調制響應是一個左右對稱的向量，而其他波束分量的調制響應則不具備對稱特性[16]。

2.1 換能器陣列輸出信號

由n個換能器陣元構成陣列，在t時刻換能器陣列的輸出為：

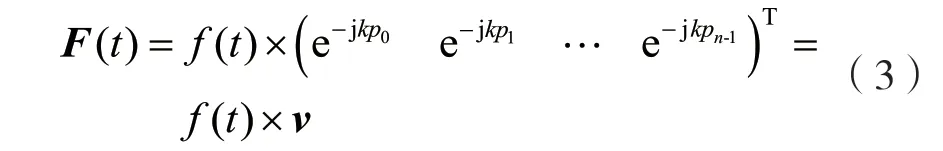
2.2 FIR 算法

利用基本的限長單位沖激響應（Finite Impulse Response，FIR）算法對n個陣元的陣列輸出信號進行處理，即對各陣元輸出進行加權和計算，計算公式為：

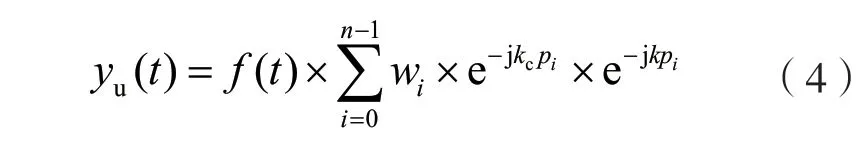
式中：yu(t)為n個陣元加權和的系統響應輸出。

以矩陣形式表示為：

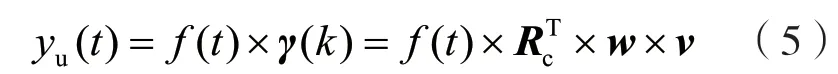
式中：γ(k)=RcT×w×v為系統對波數k分量的系統增益；為調向矢量；kc為主響應軸波數；為權矩陣；為陣列流形矢量。

2.3 對稱偏轉調制

對稱偏轉調制方法是陣列調向[17]這一基礎方法的延伸，通過多次對稱調向來獲得偏轉調制矩陣。

在主響應軸波數兩側一定范圍內，等間隔對稱設置m個偏轉角度，分別得到相應的m個偏轉矢量：

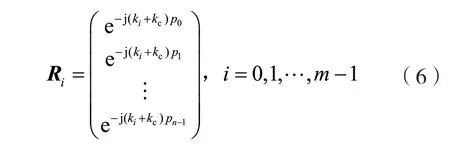
式中：ki為第i個偏轉方向的波數。

則由m個偏轉角度得到的偏轉調制矩陣為：

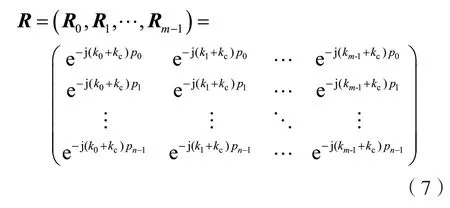
可得系統調制增益為：

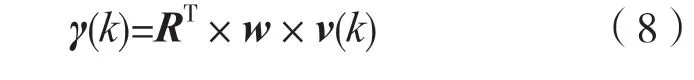
系統調制響應輸出即為一個m維向量：

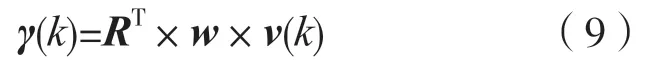
3 自對稱匹配濾波

根據FIR 濾波器基本特性可知，對于主響應軸方向的波束分量，偏轉調制響應是一個左右對稱的向量，而其他波束分量的調制響應則不具備對稱特性，因此將調制響應向量反轉后進行匹配濾波[18]，即可獲得主響應軸波束分量的強度，其表達式為：

式中：JM為M維的方陣，表達式為其反對角線上的元素為1，其他元素為0。偏轉調制后的自對稱匹配濾波環節使得各個偏轉角度的輸出先進行對稱，然后與對稱之前的輸出逐個相乘，最后累加獲得系統的輸出。

由于不具備左右對稱的特性，因此非主響應軸方向的波束分量將被大幅抑制，而主響應軸波束分量則可以得到較高的增益。

4 仿真結果與分析

4.1 仿真實驗

4.1.1 仿真1

陣列采用8 個陣元的標準線陣，陣元間距d設置為信號波長λ的一半，即d=λ/2。采樣快拍數設置為K=1 200。基本FIR 算法的8 陣元陣列響應仿真如圖1。

通過分析仿真圖1，可發現當為基本FIR 算法的8 陣元陣列響應時，陣列方向圖的主瓣半寬的正弦為0.12。

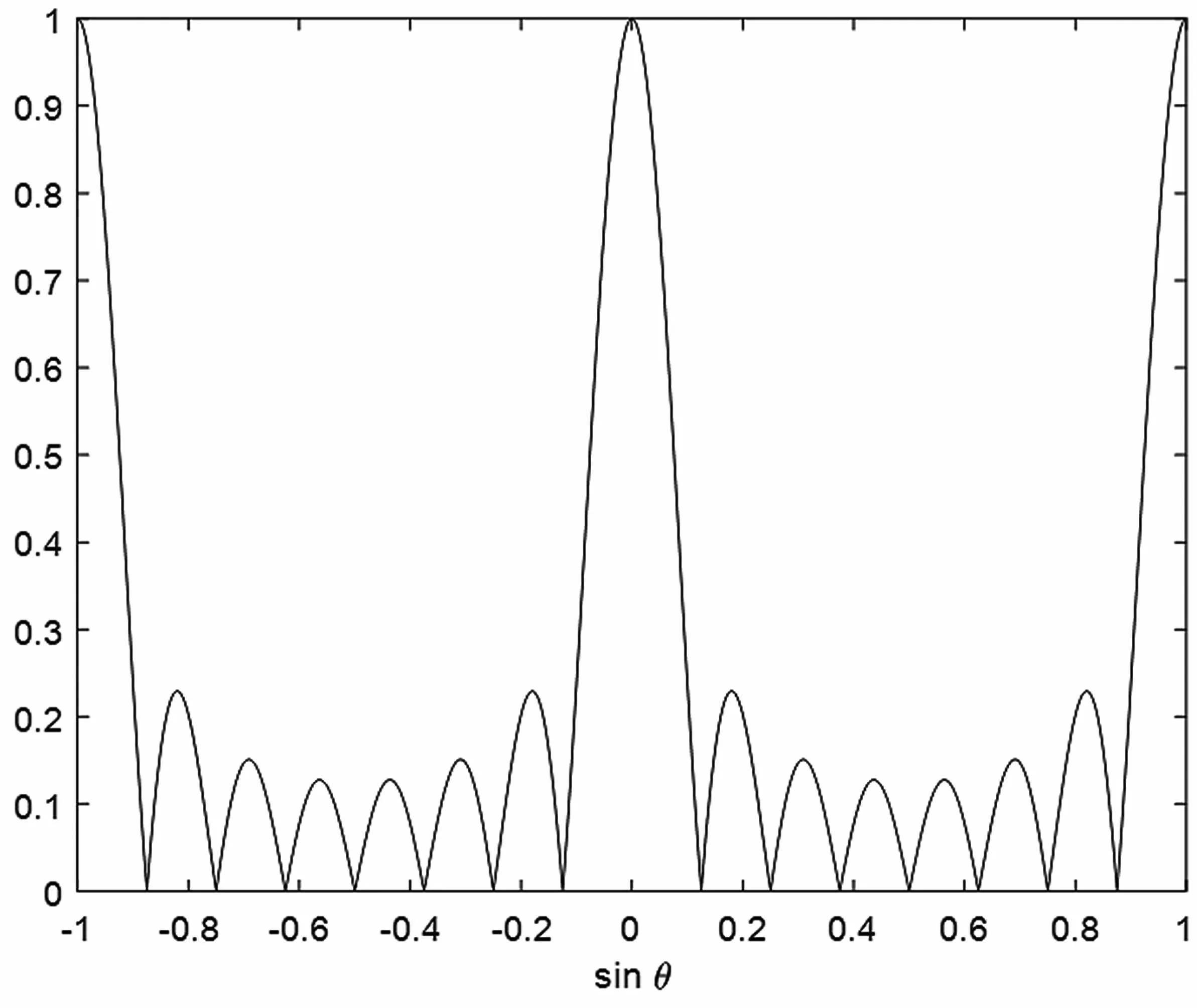
圖1 基礎FIR 算法陣列方向圖

4.1.2 仿真2

陣列采用8 個陣元的標準線陣，陣元間距d設置為信號波長λ的一半，即d=λ/2。采樣快拍數設置為K=1 200。對對稱空間濾波器組自匹配波束形成算法進行仿真實驗，對稱偏轉的角度設定為±3°，偏轉次數設置為11 次，結果如圖2 所示。

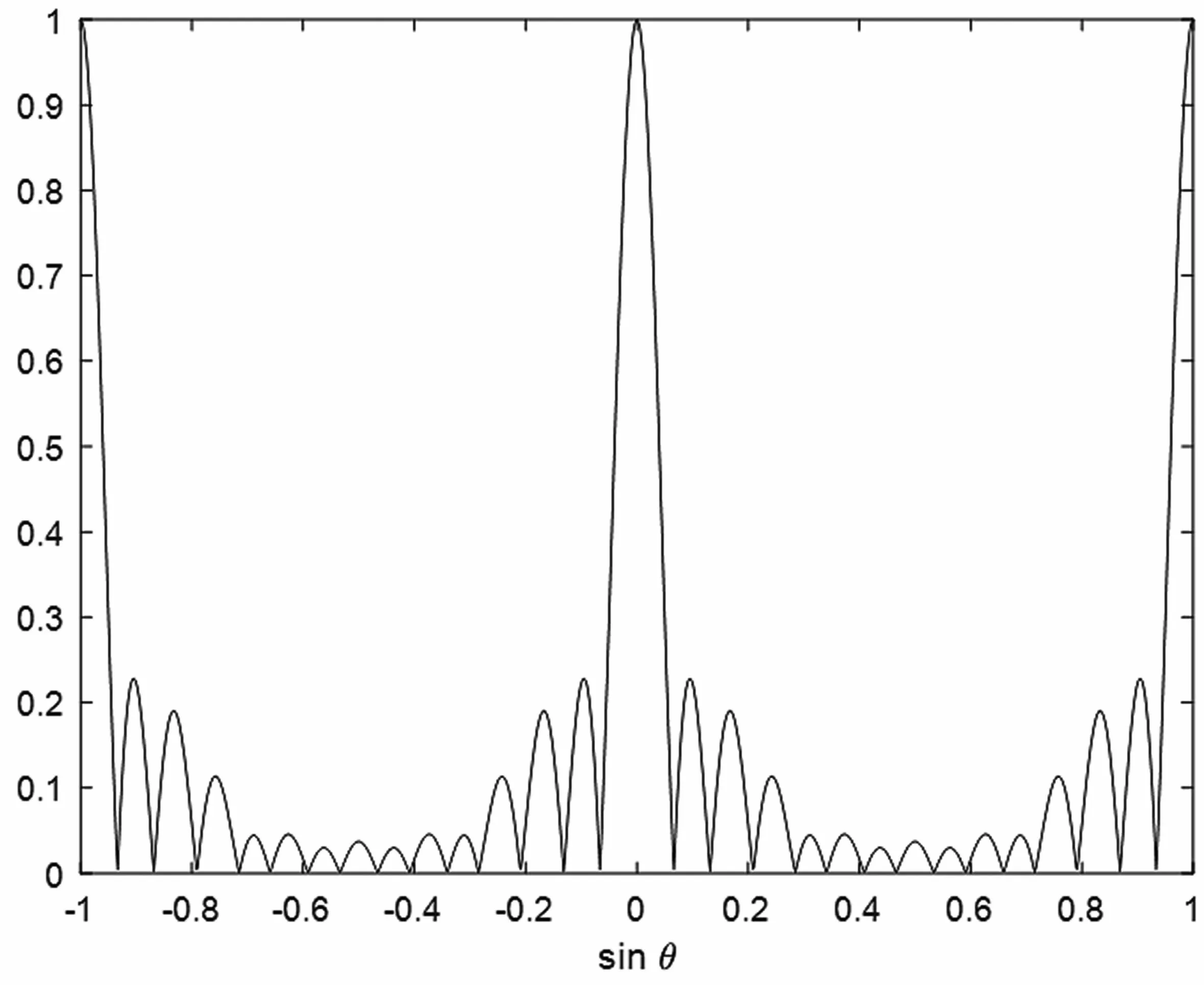
圖2 空間自匹配濾波波束形成算法陣列方向圖

通過仿真圖2 發現，相較于基礎的FIR 算法，通過對稱空間濾波器組自匹配波束形成算法得到的陣列方向圖主瓣更窄，對不同波束分量的濾波效果改善明顯。本方法得到的方向圖主瓣角度半寬的正弦僅僅是0.067，主瓣寬度降低到約為基本的FIR算法的一半。通過本文提出的算法，突破了主瓣瑞利極限，有效地收窄了主瓣寬度。

當兩個及兩個以上的不同頻率信號輸入非線性電路中時，會產生干擾，這種干擾稱為互調干擾[19-20]。在本方法的實際運行中存在信號互調的現象。

假設僅有兩個信源存在時，則：

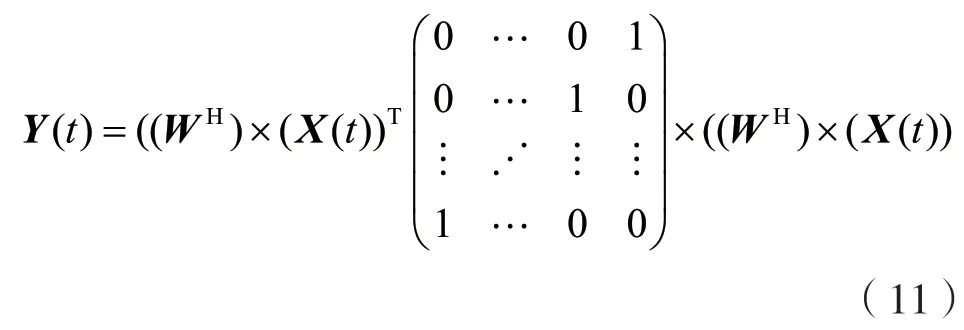
式中：WH為權矢量矩陣。

X(t)的表達式為：

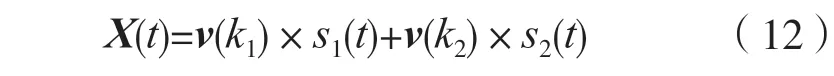
令Z1(t)=v(k1)×s1(t)，Z2(t)=v(k2)×s2(t)，則可推出：

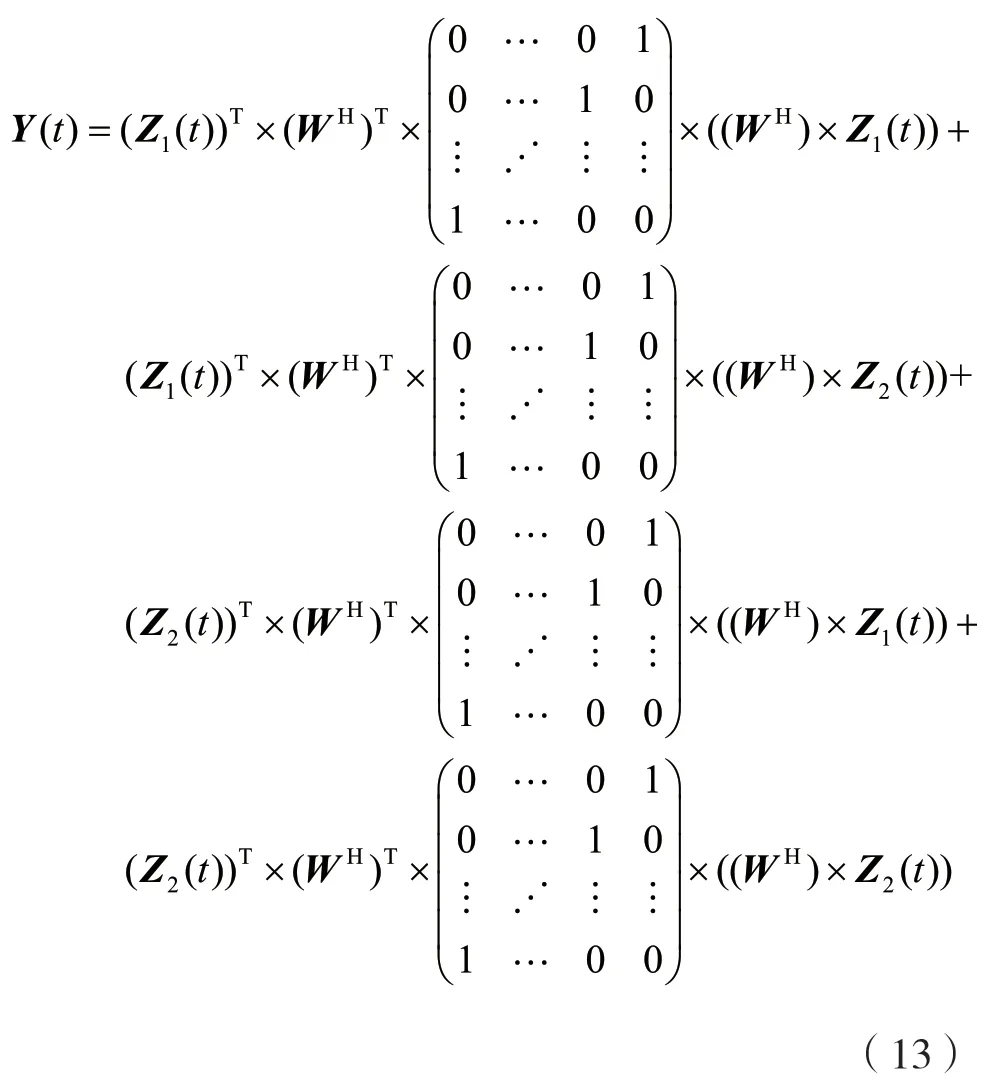
可以看出，干擾信號在經過自對稱匹配濾波器后會對期望信號產生干擾，兩個波束分量之間存在互調。

兩個信號之間互調的影響為：

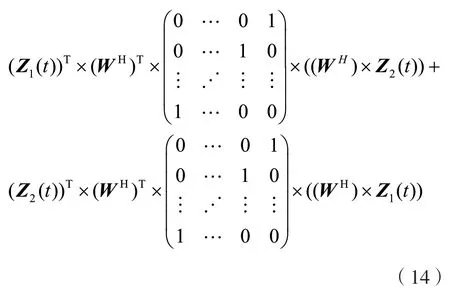
通過對上述公式的分析可以看出，兩個信號的互調影響程度可以通過分析任一項干擾增益來獲得。

4.1.3 仿真3

本文以第1 項互調干擾為例，通過兩個流形矢量在不同入射角度時干擾增益的大小來判定其誤差情況。當兩個信號以各自的入射角度被陣元接收到信號時，會得到其對應的信號互調影響的大小。

設置16 陣元的陣列，陣元間間隔為d=λ/2 的均勻線陣，接收信號源為遠場窄帶信號。陣元的采樣快拍數為1 200，波速為3 000 m/s。在-3°到3°之間平均選取了11 個偏轉角度構造權矢量矩陣，將入射信號從-90°到90°，以1°為標準選取181 個入射點，可得到仿真圖，如圖3。

上述三維仿真圖表示在兩個入射信號情況下，其入射角度在-90°到90°之間變化時信號互調所產生誤差的大小。由圖3 分析可知，大多數情況下兩個信號互調產生的影響基本可以忽略不計。當兩個信號中有一個信號為0°入射時，另一個信號的入射角度會與之有一定的信號互調影響。

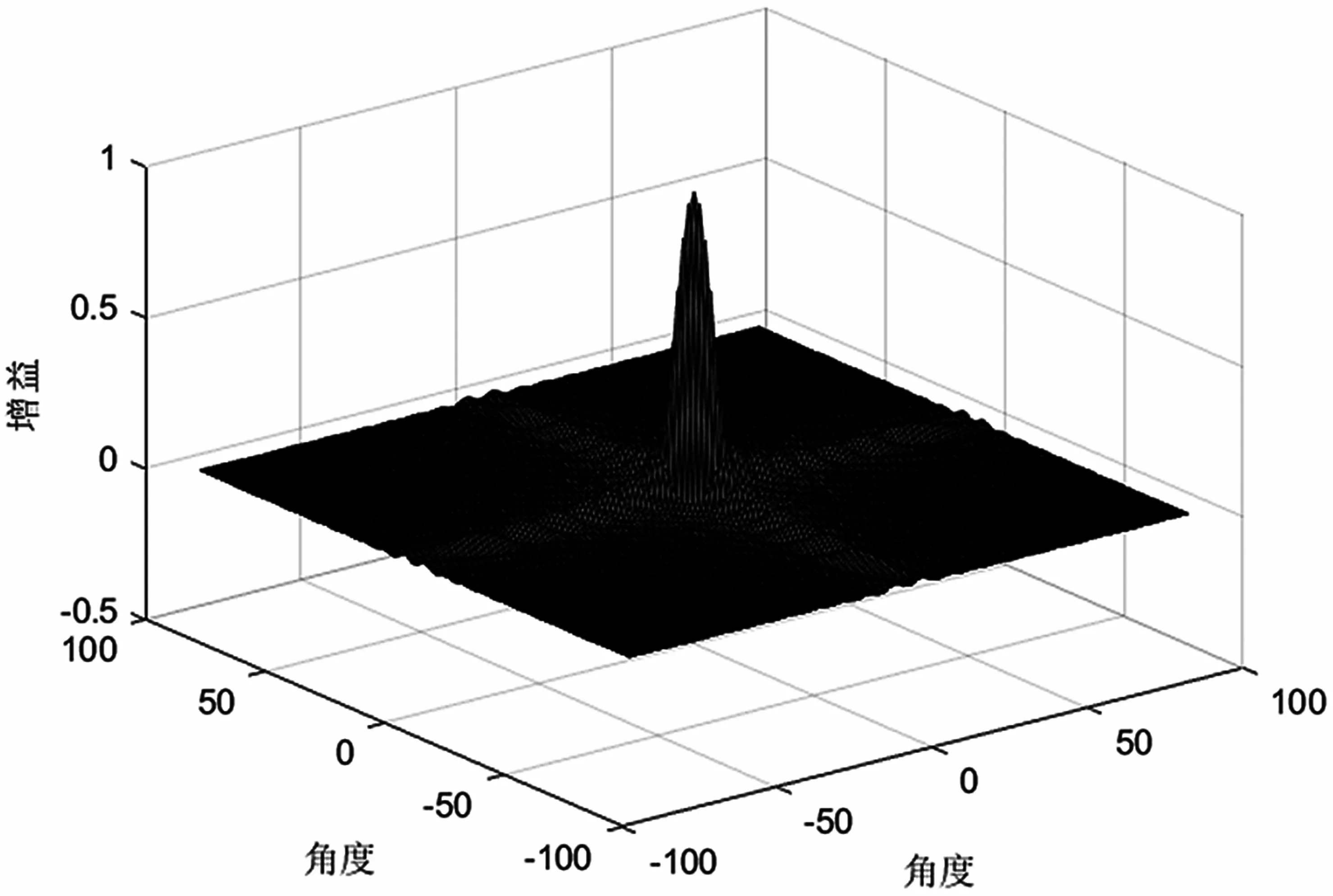
圖3 兩信號源不同角度入射下信號互調增益

由此可知，期望信號的入射角度為0°的情況下，兩個干擾信號之間的互調影響基本可以忽略，只有期望信號與干擾信號之間會有一定的互調影響，但是也比較小。

4.1.4 仿真4

如圖4 所示為進一步對仿真結果進行分析，分別對兩個入射分量進行限定選取，分為以下三種情況：曲面正對角線方向，即兩個分量具有相同的濾波，也就是某一個分量與其自身的濾波輸出；曲面反對角線方向，即兩個分量具有對稱的濾波；水平中央方向，即主軸分量與其他分量的濾波。

通過分析可以發現，只有在期望信號與干擾信號互調時，才會出現較大的互調干擾。干擾信號在入射角度遠大于偏轉角度的情況下，它們之間的互調影響可以從三維圖上清晰地看出基本為0。從圖4（c）可以看出，只有在干擾信號的入射角度在偏轉角度之內或者接近偏轉調制角度時，期望信號與干擾信號之間才有比較大的干擾增益；當遠離偏轉調制的角度時，干擾信號與期望信號之間的互調影響很小。

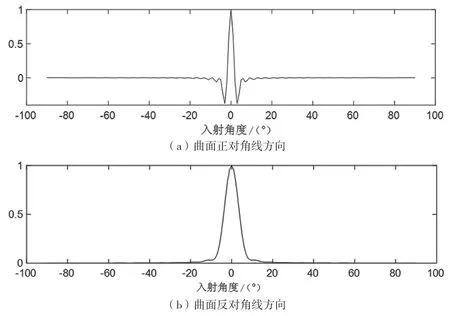
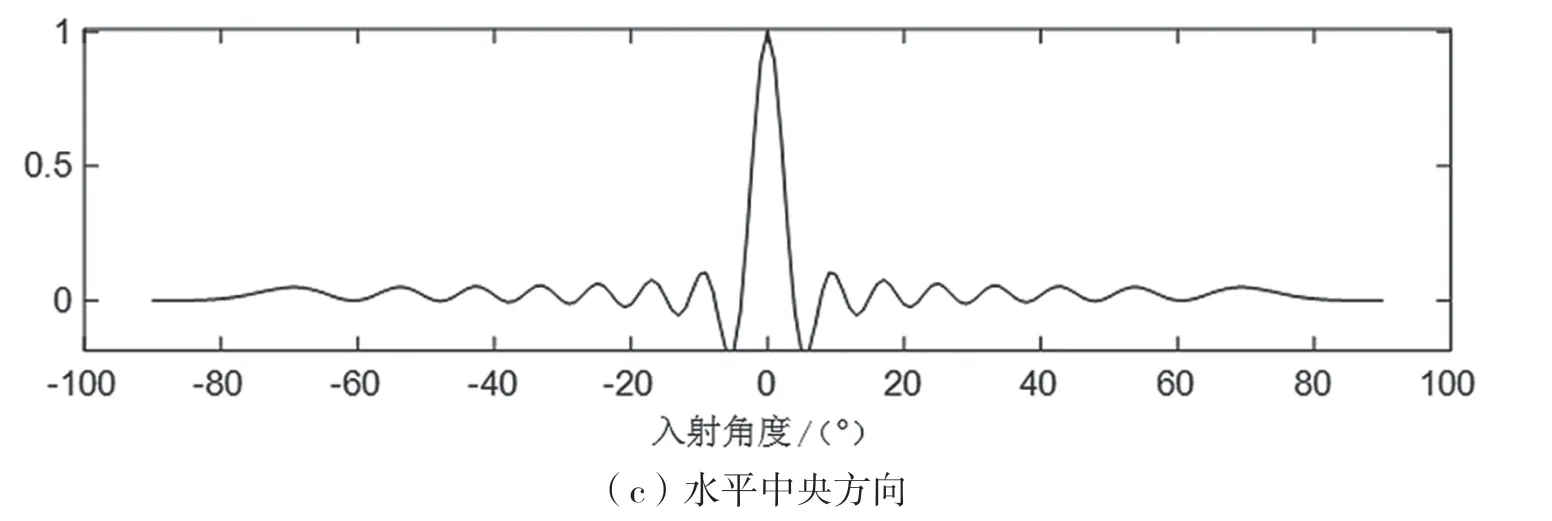
圖4 兩波束分量特定情況下互調分析

當曲面正對角線即兩個分量具有相同濾波時，-10°到10°之間具有較大的增益，正對主軸方向的期望信號具有最大的增益。其他方向的干擾信號，當入射角度遠大于選取的偏轉調制矩陣的偏轉角度時，其互調影響很小，相對于主軸方向的大增益來說基本可以忽略不計。也就是說，當干擾信號遠大于偏轉調制角度時，信號自身的增益對于仿真結果的影響可以忽略不計。結合三維仿真圖的結果可以發現，只有在期望信號與干擾信號互調時才有較大的增益影響，干擾信號在入射角度遠大于偏轉角度的情況下，它們之間的互調影響近似為0。

4.2 分析與結論

通過以上幾個方面的分析，可以看出本文方法在干擾信號來波方向的入射角比較大的情況下，能夠得到較好的實現，并且通過選取遠小于最小入射角的偏轉角度構造偏轉調制矩陣，可以最大限度地減小信號互調影響對本方法帶來的影響。

當然，降低本文方法所帶來的信號互調影響也是很有必要的。從式（13）中可以看出，信號的互調是必然存在的。為進一步優化算法性能，可以通過引入經典的自適應波束形成算法對權矢量矩陣進行約束處理。

5 引入LCMV 算法優化

經典的LCMV 算法可以通過設置權值矢量，使得波束方向圖在特定來波方向上生成零陷[21]。在本文所提方法中，同樣可以通過設置權值矢量，并帶入權矢量矩陣中，獲得一個可以在特定方向上得到零陷的權矢量矩陣，從而在已知的干擾信號來波方向生成零陷，抑制干擾對期望信號的影響。

設置16 陣元的陣列，陣元間間隔為d=λ/2 的均勻線陣，接收信號源為遠場窄帶信號，進行仿真實驗5。陣元的采樣快拍數為1 200，波速為3 000 m/s。在-3°到3°之間平均選取了11 個偏轉角度構造權矢量矩陣，將入射信號從-90°到90°以1°為標準選取181 個入射點，假定干擾信號以-20°、30°為入射角度。引入LCMV 算法后對本文算法可得到仿真結果如圖5 所示。

圖5 引入LCMV 算法零陷約束

從三維仿真圖5 可發現，仿真圖在-20°和30°的干擾方向上形成了較深的零陷，期望信號與干擾信號在以-20°和30°為入射角度入射時，產生的信號互調影響受到了極大的抑制，說明所提方法能夠有效地去除在空間自匹配濾波過程中由于信號互調所產生的干擾。

設置16 陣元，陣元間間隔為d=λ/2 的均勻線陣，陣元的采樣快拍數為1 200。空間中有3 個完全不相干的信源，來波方向角度為[0,-40°,20°]，對應的信源波束為[0,-0.64,0.34]。對經典的LCMV 算法和LCMV 優化的本文算法進行仿真對比，結果如圖6所示。

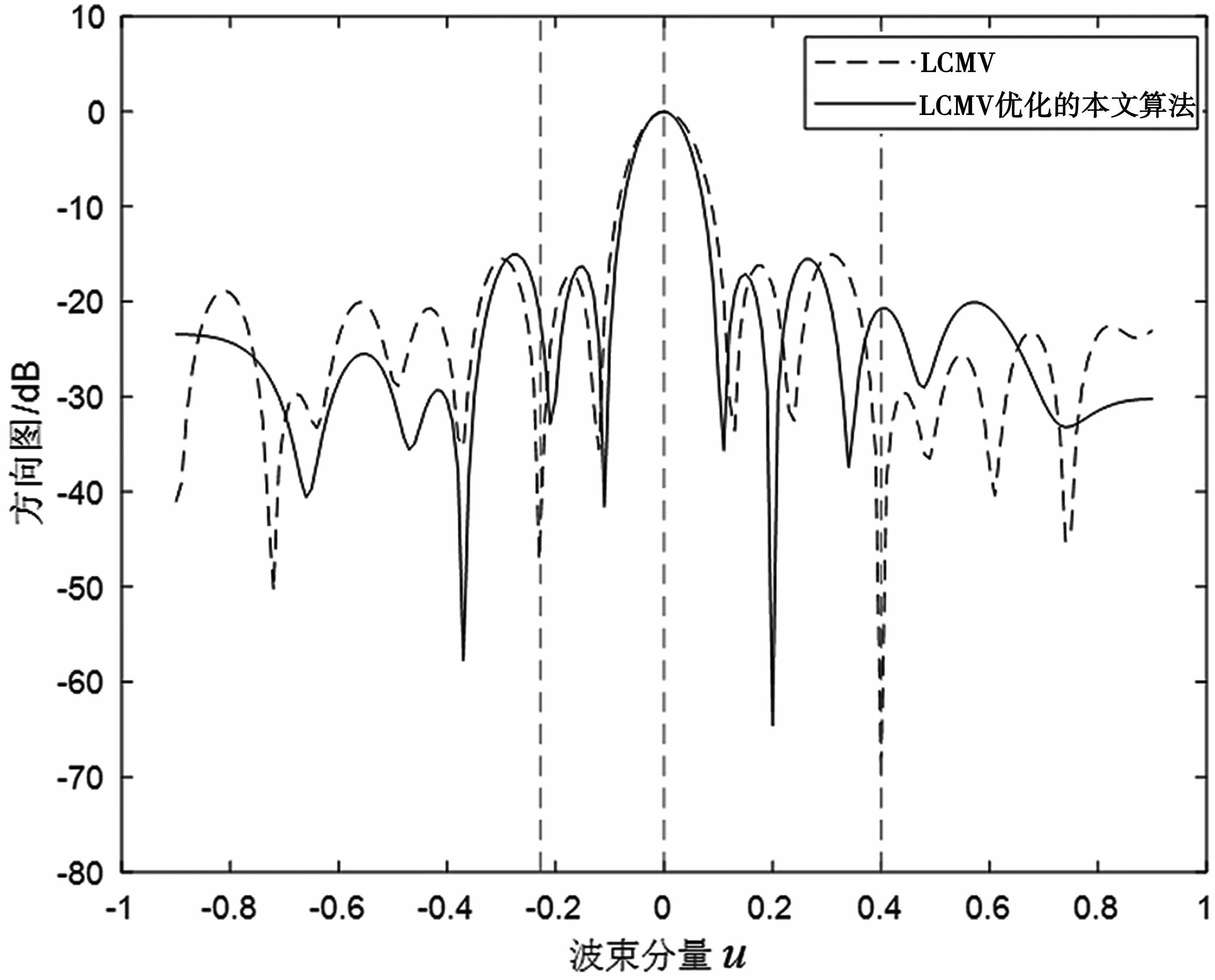
圖6 LCMV 算法和LCMV 優化的本文算法

通過圖6 可知，LCMV 算法優化后得到的偏轉調制線性約束最小方差（Deflect Modulation Linearly Constrained Minimum Variance,DM-LCMV）波束形成算法，可以在干擾信號的來波方向（即仿真圖中光標位置）形成零陷，進一步降低干擾信號對系統的影響。同時，陣列方向圖的主瓣半寬由LCMV 算法的0.13 收窄至0.11，陣列方向圖的主瓣寬度突破瑞利極限，算法的性能得到了提升。

6 結語

本文提出了一種基于對稱空間濾波器組自匹配的波束形成算法，能夠有效地得到主瓣更窄的陣列方向圖，突破主軸的瑞利極限。該方法通過對換能器陣列得到的輸入信號進行對稱偏轉調制，獲得系統調制響應的輸出，然后對其進行自對稱匹配濾波。由于對于主響應軸方向的波束分量，偏轉調制響應是一個左右對稱的向量，而其他波束分量的調制響應則不具備對稱特性，因此將調制響應向量反轉后進行匹配濾波，可獲得主響應軸波束分量的強度，在此情況下，陣列的方向圖突破了主瓣瑞利極限的限制。而由于信號互調的存在，本文又引入了LCMV 算法對干擾信號進一步抑制，在干擾方向上形成零陷，提高了算法的性能。