基于神經網絡和智能優化算法的水電機組自適應PID控制

黃金龍，秦小元，沈博淵，夏 晨，陳金保，肖志懷

（1.向家壩水力發電廠，四川宜賓 644612；2.南京南瑞繼保電氣有限公司，南京 211101；3.武漢大學水力機械過渡過程教育部重點實驗室，武漢 430072；4.武漢大學動力與機械學院，武漢 430072）

0 引 言

中國是水資源開發和利用大國，水電機組裝機容量世界領先。近年來，隨著金沙江、雅礱江等流域巨型水電站的相繼建成和投入運行，我國電力系統中水力發電占比進一步提高，加之風、光等可再生能源在電網中的滲透率增加，調度部門對水電調節的靈活性和可靠性要求日益嚴格［1］。在電網的調節過程中，水電機組主要通過承擔黑啟動、冷熱備用、調峰調頻等關鍵任務來滿足系統功率、頻率和電壓的穩定，保證電能質量。在水電占優電力系統中，低頻振蕩是重要的動穩定問題之一，與水電的負阻尼效應直接相關。大量研究表明，水輪機調速器控制參數設置不合理是造成此類現象的主要原因［2］。我國絕大多數電站的水輪機調速器根據不同的控制模式采用提前整定好的一組或幾組控制參數，并且在機組運行過程中，這些控制參數的設定值保持不變。水電機組所具有的強非線性、非最小相位特性決定了系統在不同水頭和負荷下的穩定性是不同的［3］。固定的PID 參數無法根據機組的運行工況進行適應性地調整，在某些工況下可能會出現調節品質惡化，甚至造成機組振蕩、解列等嚴重問題。因此，水電機組的優化控制是提高調速器調節品質和電力系統穩定性的重要方式。

PID 控制策略具有結構簡單、可靠性強，參數物理意義明確、調節方便等優點，在工業控制過程中得到了廣泛應用［4］。但對于復雜的非線性系統，僅靠一組PID 參數難以滿足多工況的控制要求。目前，水電機組的優化控制主要從PID 控制策略優化和先進控制算法兩個方面開展研究［5］。在PID 控制策略優化方面，可以通過優化控制器結構或參數或借助智能算法輔助調節等方式提高PID 控制器的控制性能以及PID 參數對機組工況的自適應性［6，7］。高菘等人利用生物地理學優化算法對水電機組的PID 參數進行了優化，并通過對比試驗驗證了該算法在控制參數優化方面的優勢［8］。Chen等人將分數階PID控制器引入水輪機調節系統，并利用改進的引力搜索算法優化控制器參數，得到了滿意的控制性能［9］。通過設計模糊系統以實時優化PID 參數，能夠實現調速器控制參數的自適應調整［10-12］。在先進控制算法方面，滑模控制、預測控制、模糊控制、神經網絡控制等在水電機組控制中的理論研究得到了較快發展，是最具潛力的幾種先進控制算法［13-16］。吳道平等人設計了適用于非最小相位系統的水電機組改進滑模控制策略，并對滑模控制參數進行了優化，克服了傳統滑模控制存在的假穩定現象［1］。Xiao和王濤等人分別設計了用于水電機組的神經網絡控制器，提升了水電機組的控制性能［17，18］。Zheng 等人開發了基于樹種算法的多模態預測控制算法，并在多種工況下證明了該控制器在機組電壓和頻率調節中的優異性能［19］。

雖然先進控制算法對水電機組的優異控制性能在仿真中得到了充分驗證，但算法的復雜性和可靠性使得其距離實際應用還需時日，而在以模糊系統為代表的自適應PID控制中，知識的獲取也需要專家經驗的支持，增加了算法設計的難度。考慮到目前水輪機調速器仍以PID 控制為主，本文基于智能優化算法和神經網絡，設計了一種易于實現的水電機組自適應PID 控制器。首先建立了水輪機的神經網絡非線性模型。其次，對水輪機非線性模型進行局部線性化處理，得到不同工況下的水輪機傳遞系數，進而建立水輪機調節系統的分段線性模型。基于該分段線性模型，利用一種改進的粒子群算法和絕對誤差時間積分目標函數，對不同工況下水輪機調節系統的PID 控制參數進行優化。最后以一系列參數優化結果作為學習樣本分別得到反映三個PID參數與機組運行工況（導葉開度和工作水頭）關系的神經網絡，進而得到水電機組的自適應PID 控制器。為驗證該控制器的性能，將其在不同工況下的控制性能與傳統的定PID 控制進行對比。結果表明，本文設計的自適應PID 控制器具有良好的工況自適應性，在不同工況下均具有比定PID 控制更優異的調節性能。

1 水輪機調節系統數學模型

1.1 調速器模型

調速器是水電機組的核心控制設備，包含控制器和隨動系統兩個部分。其主要工作原理是通過接收電網頻率波動信號調整導葉開度，使機組出力發生變化，進而保持電網的頻率穩定和功率平衡。對于本文研究的水電機組，控制器采用并聯PID 型控制策略，隨動系統主要由比例閥、中間接力器、主配壓閥和主接力器構成。調速器整體傳遞函數如式（1）所示［20］。

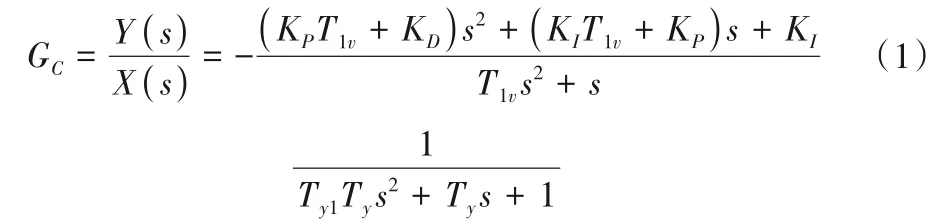
式中：KP、KI和KD分別為控制器的比例、微分和積分系數；T1v為微分環節時間常數；Ty1和Ty分別為中間接力器和主接力器反應時間常數；Y為導葉開度；X為機組轉速。

1.2 發電機模型

發電機模型由運動方程和電磁方程組成。當考慮電氣量暫態或次暫態過程時，需要使用三階及以上高階發電機模型。由于本文研究不涉及電力系統建模，僅考慮調速器的頻率控制模式，因此負載可用常數表示，發電機及負載傳遞函數采用一階慣性環節，如式（2）所示［20］。

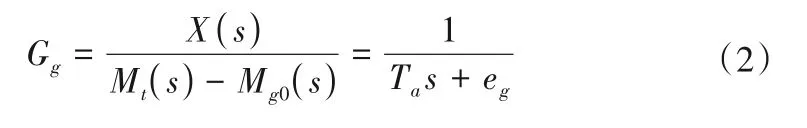
式中：Ta為機組慣性時間常數；eg為發電機負載自調節系數；Mt為水輪機力矩；Mg0為負載力矩。

1.3 水力系統模型

水電站水力系統自上而下一般包含水庫、引水管道、調壓室、水力機組、尾水隧洞等水力元件。根據壓力管道的長度以及仿真工況，引水系統可采用不同的水擊模型。在調節系統小波動條件下，當壓力管道長度小于600～800 m 時，一般采用剛性水機模型，反之采用彈性水擊模型；對于調節系統大波動過程，一般采用特征線法［21］。本文研究的機組壓力管道長度較短，因此采用如式（3）所示的剛性水機模型［20］。

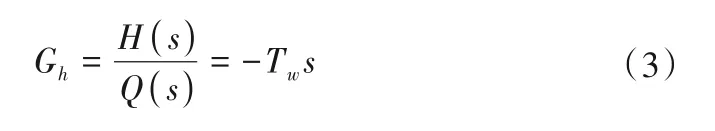
式中：Tw為水流慣性時間常數；H為水輪機水輪機工作水頭；Q為水輪機過流量。

1.4 水輪機模型

水輪機模型分為線性模型和非線性模型，均可由模型試驗得到。線性模型以傳遞系數表示，可用于調節系統小波動仿真；非線性模型一般利用插值、神經網絡等方法對模型試驗數據進行擬合，可用于調節系統大波動仿真。水輪機線性和非線性模型分別如式（4）和（5）所示［20］。

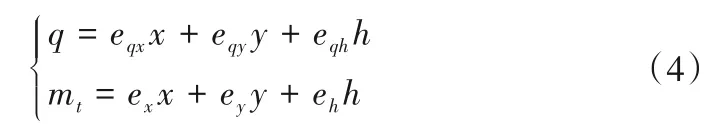
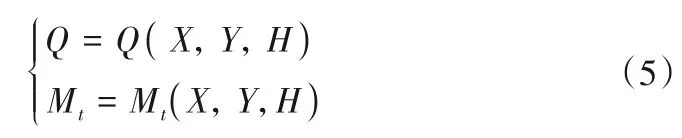
式中：eqx、eqy和eqh分別為水輪機流量對轉速、導葉開度和水頭的傳遞系數；ex、ey和eh分別為水輪機力矩對轉速、導葉開度和水頭的傳遞系數；Q為水輪機流量；Mt為水輪機力矩；q、mt、x、y和h分別表示水輪機流量、力矩、轉速、開度和水頭的偏差相對值。

聯合各子系統的數學模型，可得到水輪機調節系統的分段線性化模型，如圖1所示。在該模型中，水輪機的傳遞系數隨工況發生變化，當指定某一特定工況時，可將水輪機非線性模型在該工況處線性展開，求得該工況下水輪機的傳遞系數。傳遞系數的計算方法除了傳統方法之外，還可采用基于神經網絡的求導方法，具體內容見文獻［22］。

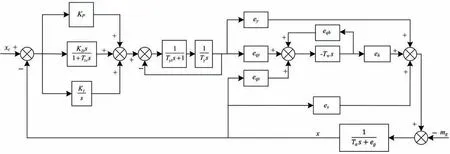
圖1 水輪機調節系統的分段線性化模型Fig.1 Piecewise linearization model of hydraulic turbine governing system

2 自適應PID控制器的設計

為設計適應于水輪機工況變化的PID 控制器，首先需要獲取機組運行工況與最優PID 參數的對應關系，其次利用傳統數學或人工智能方法構建映射這種復雜關系的非線性函數。基于上述思想，本文設計了基于智能優化算法和神經網絡的水電機組自適應PID 控制器，主要步驟如下，相應的流程圖如圖2所示。

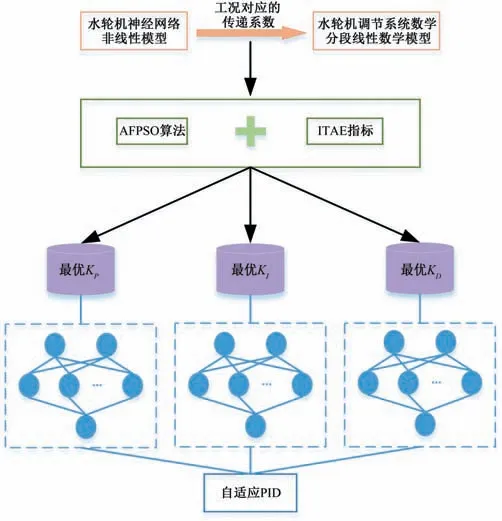
圖2 自適應PID控制器的設計流程圖Fig.2 Design flow chart of adaptive PID controller

（1）基于模型綜合特性曲線、飛逸特性曲線和其他邊界條件構成的學習樣本建立水輪機的神經網絡模型，詳細建模方法見文獻［22］。

（2）將機組整個運行工況按導葉開度和水頭均勻地劃分為若干工況點，利用文獻［22］提出的神經網絡求導法計算不同工況點處的水輪機傳遞系數，得到全工況下水電機組分段線性模型。這樣做的目的是降低模型的復雜性，節約計算時間。

（3）基于系統分段線性模型，以時間誤差積分（ITAE）指標為目標函數，利用一種性能優異的自適應模糊粒子群算法［23］優化不同工況點處的PID 控制參數，得到若干對應不同工況的最優PID參數。

（4）將若干工況點及其對應的最優PID參數作為學習樣本，以標準BP 神經網絡作為擬合工具，通過一定時間的訓練得到3個反映不同的最優PID 參數與工況關系的神經網絡，分別記為KP神經網絡、KI神經網絡和KD神經網絡。它們的輸入均為導葉開度和水頭。

（5）將構建的3 個用于PID 參數實時調整的神經網絡嵌入傳統的PID 控制器中，得到適應于水輪機工況變化自適應PID控制器。

通過以上步驟得到的自適應控制器的結構框圖如圖3 所示。可以看出，相比傳統的PID 控制器，該控制器的PID 參數可通過輸入的導葉開度和水頭，經過3 個不同的神經網絡計算求得，是一種在線PID 調整方法。由于神經網絡的訓練數據是各個工況下的最優PID 參數，因此能夠保證PID 控制器在不同工況下都具有良好的控制效果。

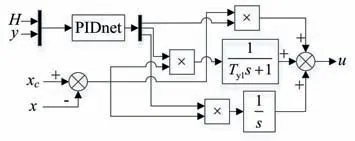
圖3 水電機組自適應PID控制器Fig.3 Adaptive PID controller of hydropower unit

3 仿真驗證和結果分析

本文以某電站為例，驗證本文提出的自適應PID 控制器在大型混流式水電機組上的應用效果。機組的基本參數為：額定功率812 WM，額定流量890 m3/s，額定轉速75.0 r/min，額定水頭100 m，水頭變化范圍為86.1～114.2 m，帶負荷條件下開度變化范圍為20%～100%。模型的基本參數為：T1d=0.1，Ty1=0.041，Ty=0.46，Tw=1.39，Ta=9.3，eg=0.086。根據水頭和導葉開度的變化范圍，導葉開度每隔10%作為一個工況點，水頭每隔2 m作為一個工況點，因此整個運行工況將劃分為135 個工況點。根據每個工況點對應的開度和水頭，利用水輪機神經網絡模型可以得到相應的水輪機傳遞系數和水輪機調節系統分段線性模型。對各個分段線性模型的PID 控制參數按照第3 部分中的步驟（3）進行優化，得到一系列最優PID 控制參數，如圖4-6 中的灰色圓點所示。利用不同控制參數和工況之間的關系樣本訓練BP 神經網絡。為保證良好的訓練效果，對于每個控制參數，將全部樣本分為訓練樣本、驗證樣本和測試樣本，占比分別為80%、10%和10%。訓練方法采用兼具梯度下降法和高斯牛頓法優點的LM 算法。最大迭代次數為1 000。經過反復比較，神經網絡采用1 個隱含層的3 層架構，隱含層的神經元數目對于KP、KI和KD分別為6、5和5。訓練得到的與不同控制參數有關的3 個神經網絡分別如圖4-6 中的曲面所示。訓練過程MSE 變化曲線以及最終誤差如圖7所示。由圖4-6可以看出，最優PID參數樣本點基本都落在了神經網絡的擬合曲面上，表明神經網絡的訓練誤差較小，擬合精度較高，能夠很好地表征最優控制參數隨工況的變化情況。由圖7可以看出：KP、KI和KD神經網絡訓練過程中的MSE 均能達到穩定狀態，表明訓練過程中無明顯的過擬合現象；網絡預測實際誤差較小，其輸出與樣本貼合度高。

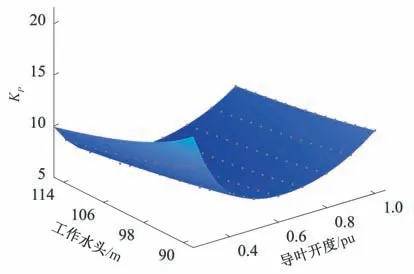
圖4 最優KP及其神經網絡擬合曲面Fig.4 Optimal KP and its neural network fitting surface

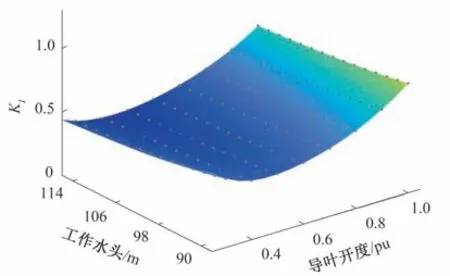
圖5 最優KI及其神經網絡擬合曲面Fig.5 Optimal KI and its neural network fitting surface

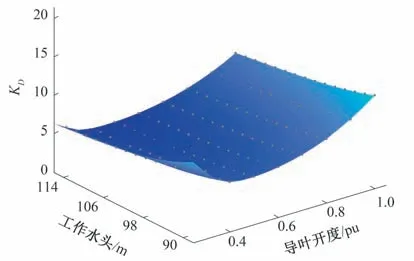
圖6 最優KD及其神經網絡擬合曲面Fig.6 Optimal KD and its neural network fitting surface

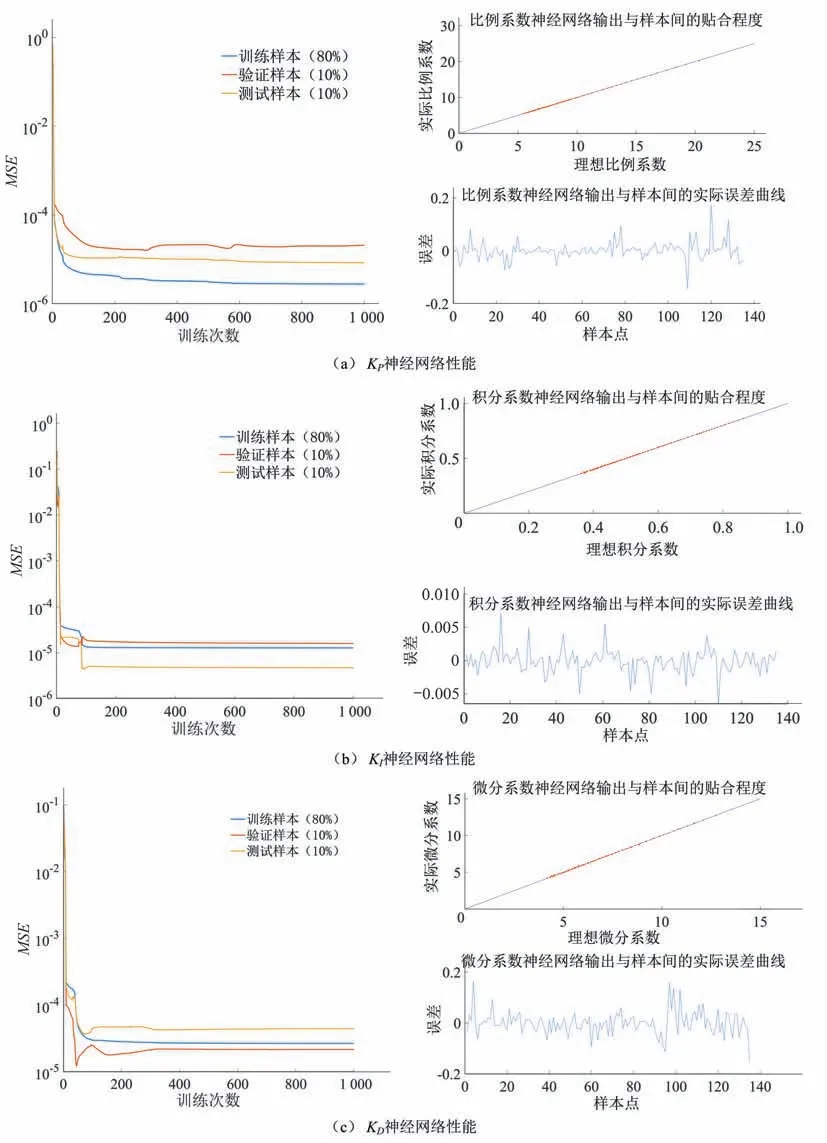
圖7 KP、KI和KD神經網絡訓練過程MSE變化曲線以及最終誤差Fig.7 MSE variation curve and final error of KP、KI and KD in the training process of neural network

最后，選擇4個不同的工況，用帶有水輪機神經網絡模型的水輪機調節系統模型進行仿真測試，驗證所提出的自適應PID控制器相較傳統的定PID控制器（以額定水頭、額定功率下的最優PID 為參考值進行設置，即KP=6.315，KI=0.463，KD=5.551）的優越性。結果如圖8所示。從圖8中可以看出，自適應PID控制器比傳統的定PID 控制有更短的上升時間和調節時間，這種優勢在低水頭工況下尤為明顯。同時，自適應PID 控制器的超調量和反調量均位于工程允許的安全范圍內，僅在個別工況下略高于傳統方法。因此，綜合來看，本文所提出的自適應PID控制器的控制性能優于傳統的定PID 控制，在不同工況下均能保證最優的控制效果，且該方法易于實施，計算量小，具有重要的應用價值。

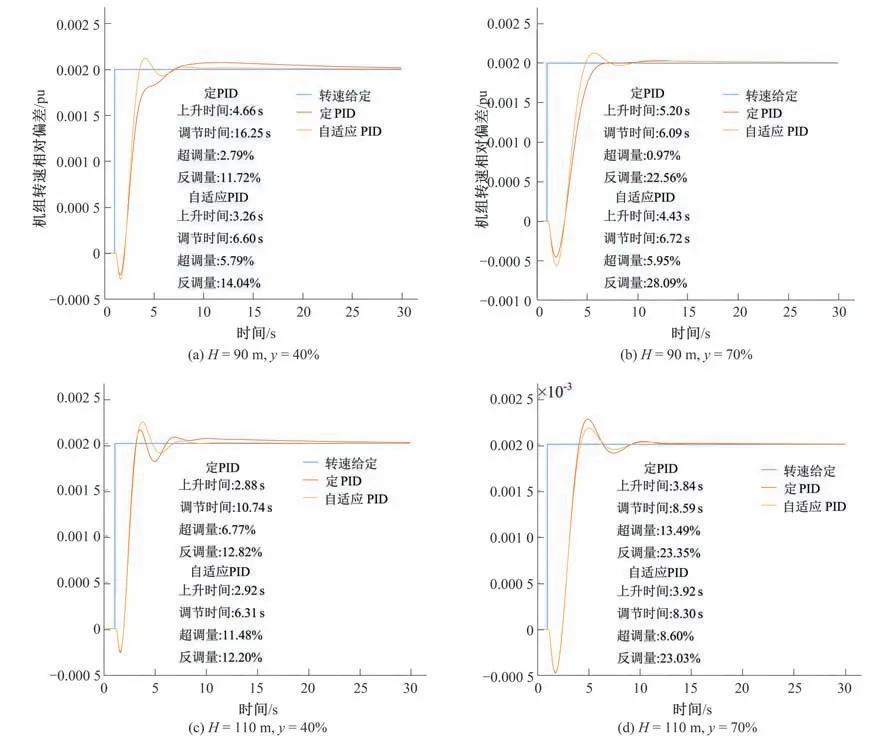
圖8 水電機組不同工況下自適應控制器和定PID控制器的調節性能對比Fig.8 Comparison of regulation performance between adaptive controller and constant PID controller under different working conditions of hydropower unit

4 結 論

電網中可再生能源的高滲透率和機組運行工況的復雜多變性使得調度部門對水電機組的控制性能提出了更高要求。在此背景下，本文針對傳統定PID 控制器難以適應工況變化的弊端，在保持原有控制器結構和不過多增加算法復雜性的條件下，基于神經網絡和智能優化算法設計了水電機組自適應PID控制器。對比試驗結果表明，所設計的控制器相較于傳統控制器，能夠根據機組工況變化自主調節PID控制參數，保證在任意工況下機組的調節性能均能滿足達到最小ITAE 指標的要求。同時，該控制器的超調量和反調量與傳統控制器相當，且均在工程要求的合理范圍內，在水電機組調速器發展中具有巨大的應用潛力。