基于顯式有限元的無(wú)砟軌道系力學(xué)行為分析與程序開(kāi)發(fā)

甘 愿，黃鈺潤(rùn)

(西南交通大學(xué)土木工程學(xué)院，四川成都 610031)

無(wú)砟軌道在我國(guó)應(yīng)用廣泛，但隨著我國(guó)高速鐵路的快速發(fā)展，行車速度越來(lái)越快，各部件的變形失效明顯加快，輪軌系統(tǒng)的動(dòng)力作用也越來(lái)越明顯，在列車長(zhǎng)期循環(huán)荷載和混凝土橋梁收縮徐變等作用下產(chǎn)生的橋墩變形和梁體結(jié)構(gòu)變形、砂漿損傷、板端上拱變形等典型病害引起無(wú)砟軌道系統(tǒng)出現(xiàn)局部脫空，嚴(yán)重影響了無(wú)砟軌道系統(tǒng)的動(dòng)力特性。

由于脫空的存在，系統(tǒng)的力學(xué)行為因可能的碰撞而演變?yōu)楦叨确蔷€性，處理此類問(wèn)題時(shí)，顯式有限元相對(duì)于隱式有限元具有先天的優(yōu)勢(shì)，其是否收斂只與時(shí)間步長(zhǎng)有關(guān)，具有良好的穩(wěn)定性，且可直接解耦，不形成大型矩陣，占用內(nèi)存空間較小。目前常用的商業(yè)顯式有限元軟件有LS-DYNA、ABAQUS/Explicit等，但由于代碼未開(kāi)源，計(jì)算過(guò)程不透明，也不利于進(jìn)行后續(xù)的參數(shù)化設(shè)計(jì)、結(jié)構(gòu)優(yōu)化、集成計(jì)算等工作，故基于顯式有限元分析方法，自主開(kāi)發(fā)了應(yīng)用于有脫空無(wú)砟軌道應(yīng)力分析的通用計(jì)算軟件。

1 有限元模型建立

1.1 無(wú)砟軌道有限元離散

目前無(wú)砟軌道的理論計(jì)算方法中運(yùn)用最多的是疊合梁模型、梁板模型和梁體模型，因?yàn)楸疚难芯恐攸c(diǎn)是軌道系統(tǒng)在有脫空狀態(tài)下應(yīng)力狀態(tài)及程序應(yīng)用可行性，故采用梁體模型。用減縮六面體實(shí)體單元離散軌道板，砂漿填充層，混凝土底座；鋼軌采用彈性點(diǎn)支承梁模型，用大轉(zhuǎn)動(dòng)空間梁?jiǎn)卧x散；考慮扣件的尺寸效應(yīng)，用彈簧單元連接鋼軌節(jié)點(diǎn)與軌道板扣件尺寸范圍內(nèi)節(jié)點(diǎn)，在不考慮地基不均勻沉降時(shí)，同樣也用彈簧單元模擬地基的支撐作用。

1.2 接觸問(wèn)題顯式有限元列式

顯式有限元處理接觸問(wèn)題的有限元理論與基本求解方法可以參考文獻(xiàn)[1-5]，在這里僅給出不考慮摩擦接觸的基本公式。

假定存在2個(gè)物體A與B，或者一個(gè)物體的2個(gè)部分A和B，在t1時(shí)刻占據(jù)空間VA和VB，其邊界分別為ΓA與ΓB，當(dāng)至t2時(shí)刻時(shí)，系統(tǒng)的空間位置或者構(gòu)型發(fā)生改變，2個(gè)物體發(fā)生了接觸。其基本控制方程與不含接觸系統(tǒng)的控制方程是一致的，但在接觸界面上需增加額外的動(dòng)力學(xué)與運(yùn)動(dòng)學(xué)條件，運(yùn)動(dòng)學(xué)約束為不可侵入條件，即對(duì)于ΓA中任意一點(diǎn)xA與ΓB中距離最近一點(diǎn)xB滿足:

gn=(xA-xB)·n≥0

(1)

式中:n為xB處ΓB的外法線。同時(shí)，法向作用力只能為壓力:

Pn≤0

(2)

根據(jù)虛功原理，系統(tǒng)的運(yùn)動(dòng)方程弱形式可以表述為:

(3)

pN=kNgN(gN<0)

(4)

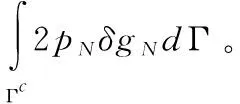
對(duì)式(3)進(jìn)行離散，可以得到系統(tǒng)的半離散:

Mü=f

(5)

式中:f=fext-fint+fc。fint為系統(tǒng)內(nèi)力，fext為系統(tǒng)外力，fc為接觸力，M為質(zhì)量矩陣，ü為加速度向量。

上式以中心差分法直接積分，由于本程序中采用集中質(zhì)量矩陣，因此可以將式(5)解耦。如已求得tn時(shí)刻的解，時(shí)刻tn+1的位移為:

(6)

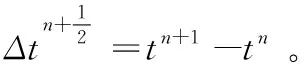
2 有限元程序設(shè)計(jì)與開(kāi)發(fā)

有限元程序的設(shè)計(jì)內(nèi)容大致可以分為前處理，分析計(jì)算，后處理3個(gè)部分。其中分析計(jì)算部分由于有限元分析方法其需要描述真實(shí)世界，需要對(duì)實(shí)例進(jìn)行多個(gè)層級(jí)的抽象與離散，天然的與面向?qū)ο蟪绦蛘Z(yǔ)言的形式邏輯吻合；同時(shí)從節(jié)點(diǎn)到單元和材料、對(duì)于各類荷載與邊界條件的處理，再到集總計(jì)算，這之間涉及到大量的數(shù)據(jù)交換與處理問(wèn)題，使得程序不可避免的變得龐大易錯(cuò)。考慮到上述問(wèn)題，本文選擇面向?qū)ο蟮腸++語(yǔ)言在Visual Studio 2019集成開(kāi)發(fā)環(huán)境下進(jìn)行設(shè)計(jì)開(kāi)發(fā)。將各層級(jí)的問(wèn)題抽象為類進(jìn)行組織，從而通過(guò)對(duì)不同類的實(shí)例化來(lái)實(shí)現(xiàn)有限元分析，提高程序的可重用性、易維護(hù)性和可拓展性。程序框架如圖 1所示。

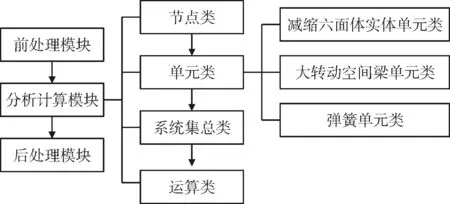
圖1 程序框架

2.1 前處理模塊

用戶在通過(guò)前處理模塊完成與有限元分析系統(tǒng)的交互，控制一系列參數(shù)完成幾何模型的建立，同時(shí)確定材料特性、單元?jiǎng)澐帧⒑奢d和邊界條件、計(jì)算終止時(shí)間，脫空位置等數(shù)據(jù)，再進(jìn)行整理并傳遞給分析計(jì)算模塊。

2.2 分析計(jì)算模塊

此模塊為有限元計(jì)算的核心，接收前處理模塊整理后的數(shù)據(jù)，實(shí)例化節(jié)點(diǎn)類，再以節(jié)點(diǎn)類為基礎(chǔ)，結(jié)合材料參數(shù)實(shí)例化單元類。其中節(jié)點(diǎn)類儲(chǔ)存了節(jié)點(diǎn)的節(jié)點(diǎn)號(hào)、位置、慣性、速度、加速度、節(jié)點(diǎn)力等信息，單元類儲(chǔ)存了此單元成員節(jié)點(diǎn)的索引、單元號(hào)、單元集中質(zhì)量矩陣、單元體積(長(zhǎng)度)、自由度等信息。再將各實(shí)例化后的節(jié)點(diǎn)與單元輸入系統(tǒng)集總類，形成整體集中質(zhì)量矩陣，遍歷節(jié)點(diǎn)，將集總得到的慣性賦予節(jié)點(diǎn)相應(yīng)的自由度，同時(shí)進(jìn)行加載與邊界條件的處理。最后再引入運(yùn)算類進(jìn)行迭代計(jì)算，其中包含節(jié)點(diǎn)內(nèi)力計(jì)算、接觸搜索、接觸力計(jì)算與沙漏力計(jì)算等過(guò)程。分析計(jì)算模塊程序執(zhí)行流程如圖2所示。

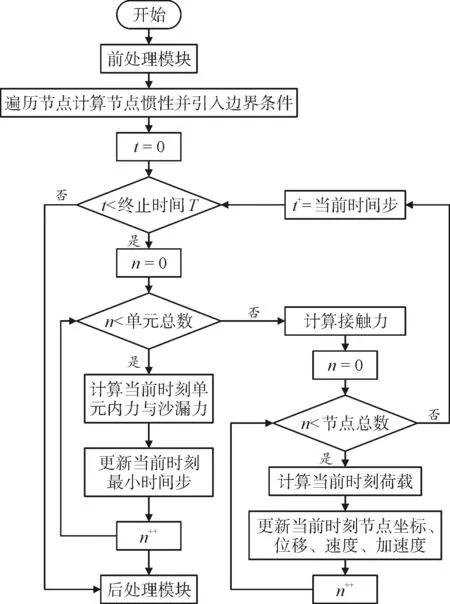
圖2 分析計(jì)算模塊程序執(zhí)行流程

2.3 后處理模塊

TECPLOT是一款功能強(qiáng)大的數(shù)據(jù)分析和可視化處理的軟件，它提供了豐富的繪圖格式，能后根據(jù)有限元分析輸出的節(jié)點(diǎn)信息生成網(wǎng)格，支持云圖繪制等有限元后處理過(guò)程中不可缺少的功能。

故本文使用TECPLOT軟件進(jìn)行可視化后處理，后處理模塊整理計(jì)算結(jié)果，根據(jù)用戶需求提取不同時(shí)間步結(jié)果，輸出為結(jié)構(gòu)化數(shù)據(jù)導(dǎo)入TECPLOT軟件。

3 程序驗(yàn)證

3.1 算例建立

本文依據(jù)CRTS Ⅰ 型板式無(wú)砟軌道結(jié)構(gòu)參數(shù)建立有限元模型作為算例，與通用顯式有限元軟件ANSYS/LS-DYNA進(jìn)行對(duì)比驗(yàn)證。

在ANSYS/LS-DYNA軟件中，用Beam161單元?jiǎng)澐周壍溃瑢?duì)應(yīng)本文程序中的大轉(zhuǎn)動(dòng)空間梁?jiǎn)卧挥肧olid164單元?jiǎng)澐周壍腊濉⑸皾{與混凝土底座板，對(duì)應(yīng)于本文程序中的減縮六面體實(shí)體單元；用Spring-damping165單元模擬地基與扣件，對(duì)應(yīng)于本文程序中的彈簧單元。

軌道采用CHN60鋼軌；扣件間距為0.625 m，剛度取50 MN/m；軌道板長(zhǎng)度為5 m、寬度為2.4 m、厚度0.19 m；軌道板選用C50混凝土，彈性模量取36 000 MPa；砂漿充填層的長(zhǎng)寬與軌道板相同，厚度為0.03 m，彈性模量取300 MPa；混凝土底座板寬3 m，厚0.3 m，選用C40混凝土，彈性模量取32 500 MPa；路基基礎(chǔ)面剛度取190 MPa/m。

為了避免邊界條件對(duì)結(jié)果的影響，建立3塊軌道板長(zhǎng)度的模型，取中間塊作為分析和研究的對(duì)象，模型如圖3所示。同時(shí)為了更好的模擬出CA砂漿離縫脫空狀態(tài)下軌道的力學(xué)行為，選擇最不利位置進(jìn)行加載。據(jù)參考文獻(xiàn)[12]可知，當(dāng)荷載加載于扣件附近的鋼軌之上時(shí)，結(jié)構(gòu)的受力最明顯，故本文在模型縱向方向8 500 mm位置設(shè)置長(zhǎng)1 500 mm，寬2 400 mm，高0.1 mm的離縫，再選擇在離縫范圍內(nèi)中間位置的扣件上方作為最不利位置，按照單軸雙輪荷載施加集中力P，示意見(jiàn)圖4，其中P取150 kN，以隨時(shí)間線性增大的方式加載于處于最不利位置的軌道上，以達(dá)到擬靜態(tài)的效果。

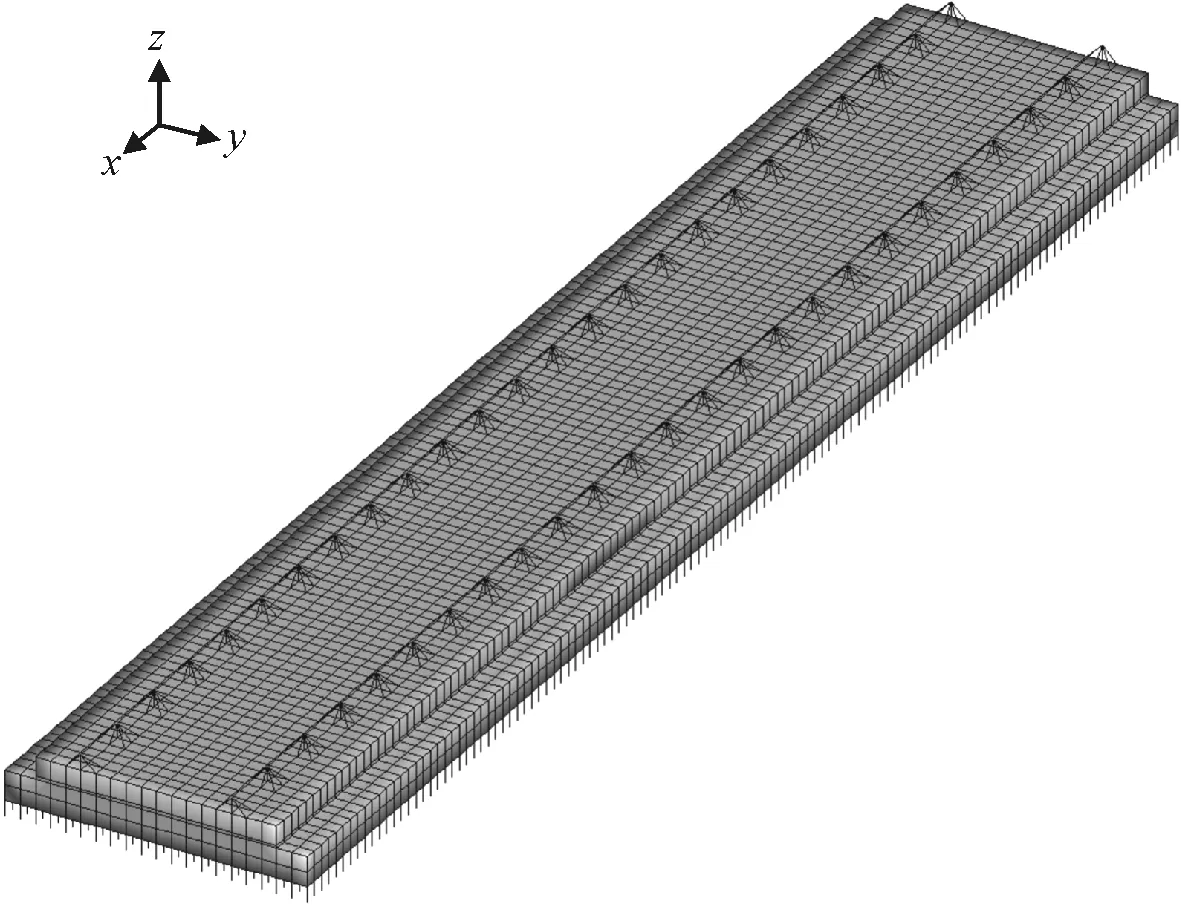
圖3 軌道模型

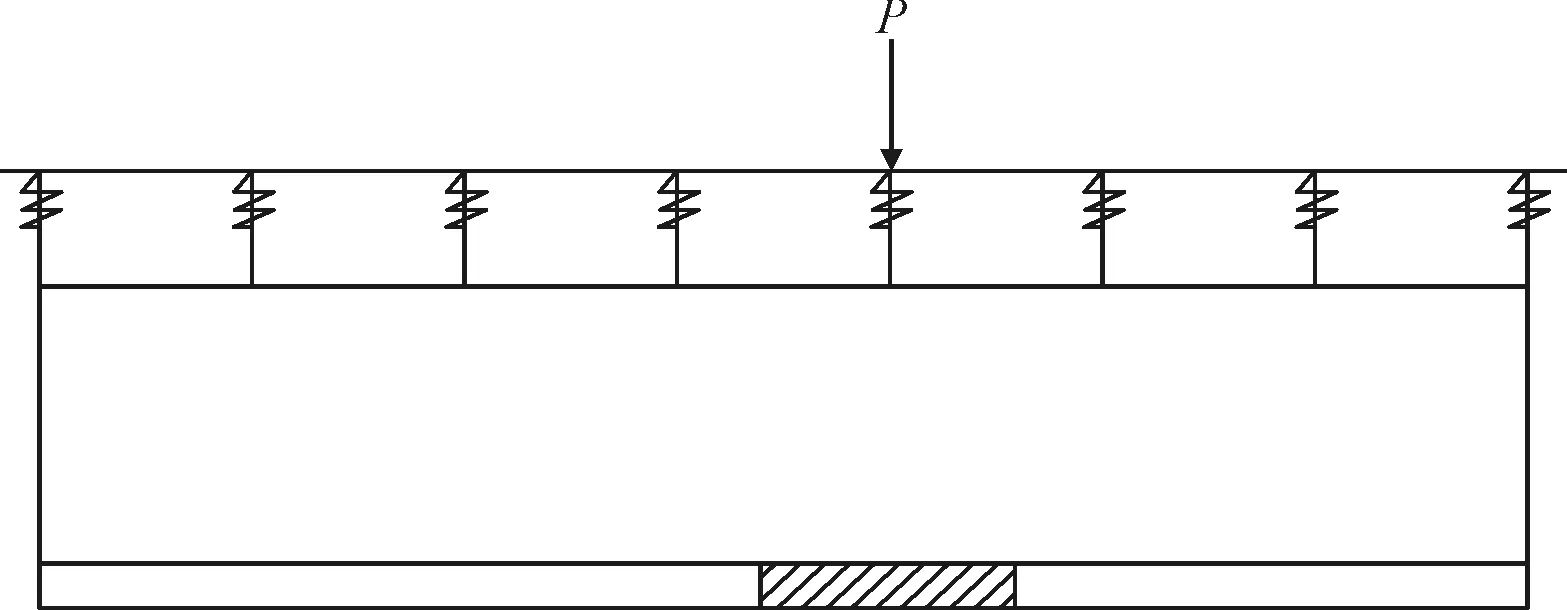
圖4 荷載示意

3.2 結(jié)果分析

提取ANSYS/LS-DYNA與本文程序結(jié)果進(jìn)行對(duì)比研究，發(fā)現(xiàn)：

(1) 考慮到有限元計(jì)算過(guò)程包含接觸分析，故提取由于離縫脫空而與砂漿發(fā)生接觸行為的軌道板部分計(jì)算結(jié)果進(jìn)行研究分析。通過(guò)對(duì)比軌道板部分最大垂向擾度關(guān)于時(shí)間的發(fā)展曲線,如圖5所示，ANSYS/LS-DYNA與本文程序結(jié)果符合良好，發(fā)展趨勢(shì)一致，最大相對(duì)誤差為2.6%，發(fā)生在0.19 s時(shí)，參考圖6軌道板部分最大垂向加速度關(guān)于時(shí)間的發(fā)展曲線，可以看到本文程序與ANSYS/LS-DYNA計(jì)算結(jié)果的相對(duì)誤差同樣也是在0.19 s附近波動(dòng)較大，而這正是發(fā)生接觸的時(shí)刻，故推測(cè)誤差可能是因?yàn)榻佑|算法部分的區(qū)別造成的。

(2) 提取1.0 s時(shí)刻模型整體的垂向擾度計(jì)算結(jié)果繪制云圖(圖7為ANSYS/LS-DYNA結(jié)果,圖8為本文程序結(jié)果)，可以看到垂向擾度分布規(guī)律一致，最大垂向擾度都出現(xiàn)在同一位置，位于加載位置扣件的下方。

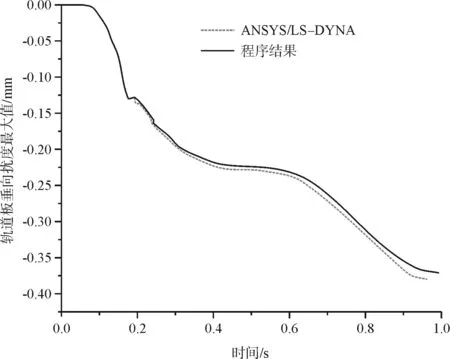
圖5 軌道板垂向位移

圖6 軌道板垂向加速度

圖7 ANSYS/LS-DYNA垂向位移云圖

圖8 程序垂向位移云圖

4 結(jié)束語(yǔ)

本文基于顯式有限元的基本思想，針對(duì)有脫空軌道板力學(xué)分析時(shí)難以處理的高度非線性接觸問(wèn)題，采用面向?qū)ο蟮腸++語(yǔ)言設(shè)計(jì)開(kāi)發(fā)了一套完整的有限元程序，并通過(guò)與通用商業(yè)有限元軟件ANSYS/LS-DYNA的對(duì)比驗(yàn)證了程序的正確性與、實(shí)用性與高效性，為有脫空軌道板力學(xué)分析計(jì)算提供了參考，為未來(lái)更進(jìn)一步的顯式有限元軟件開(kāi)發(fā)工作打下基礎(chǔ)。