高維三迭代算法對輸電線路故障的定位分析

吳衍鵬

（山東偉燁電力工程設計有限公司，山東 濟南 250000）

0 引 言

為了提高輸電效率，減少電能耗損，輸電企業常采用高壓傳輸、長距離傳輸等方式。長距離傳輸會增加輸電網的結構復雜性，以及線路故障的幾率。另外，高壓輸電線路的故障信號為暫態信號，需要進行連續性監測，否則難以識別故障信號。但是，連續性的監測，又會增加故障信號的數據量、故障信號識別的維度，增加信號監測的難度[1]。所以，500 kV輸電線路故障定位問題，一直是國內外的研究熱點。在此情況下，本文提出一種基于快速傅里葉變換（Fast Fourier Transformation，FFT）、跨組放大器等方法的高維三迭代算法，旨在提高輸電線路故障定位的準確性[2]。

1 輸電線路故障的數學模型

1.1 一維輸電線路故障的數學分析

假設1：500 kV輸電網中含有N個輸電線路，第i個線路中的諧波幅值為Si、角頻率為ωi、初始相位為αi，那么，輸電網的采樣周期Ti為

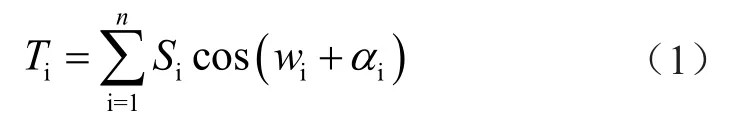
任意輸電線路Ni出現故障，該線路就會出現大幅的頻率變化，改變輸電線路的潮流分布。

假設2：任意線路Ni的頻率變化為Δfi，輸電線路狀態為e，輸電線路總數為set，那么頻率變化Δfi為

式中：e=1為正常狀態，e=-1為故障狀態；Si、ωi、αi方便諧波幅值、角頻率以及初始相位，In為采樣周期[3,4]。

1.2 高維輸電線路故障的數學分析

高維輸電線路故障定位，可以轉化為一維分析，對Δfin一階導數為

式中：i為所在線路；n為所在維度。

同樣，高維電壓、電流的一維轉化，對ΔUin一階導數為[5-7]

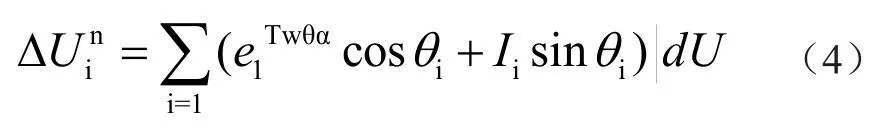
2 輸電線路故障定位的判斷模型

由于故障監測屬于連續過程，所以要將頻率變化Δf與Ti結合，構建輸電線路故障的判斷矩陣matri(ΔfTi)，具體計算如式（5）所示：

式中：ξ為線路間狀態的判斷系數，該系數的取值區間為[0,1]。

針對式（5）對輸電線路Ni的故障進行定位，定位步驟如下：

步驟1：依據式（3）對matri(ΔfTi)進行判斷，如果matri(ΔfTi)＞0，說明輸電線路存在異常，e=-1為故障狀態，并進行頻率、電壓和電流判斷。

步驟2：對電壓進行判斷，計算matri(ΔfTi)＞0，e=-1狀態下，電壓是否出現異常，具體判斷如式（6）所示。

式中：Uimin為i線路的最小電壓，Uimax為i線路的最大電壓。如果式（6）不成立，說明電壓出現異常，則進行電流測試，e=-1仍然為故障狀態。

步驟3：對電流進行判斷，計算matri(ΔfTi)＞0，e=-1、Uimin＞Ui和Ui＞Uimax狀態下，電流是否出現異常，具體判斷如式（7）所示。

式中：Uimax為i線路的最大電流。如果式（7）不成立，說明電流出現異常，說明輸電線路出現故障，e=-1為故障狀態，并記錄輸電線路Ni所在位置。

步驟4：如果Ni=Nset，說明輸電線路未出現故障，e=1。

3 500 kV輸電線路算例解析

為了驗證高維三迭代算法的有效，需要對500 kV線路進行以下分析，并與不同算法進行比較，驗證計算結果的準確性、計算時間。

對比不同維度的計算結果，如表1所示。

表1 一維的故障判斷分析

由表1分析可知，在準確性、結果相對誤差、故障的定位范圍等方面，高維三迭代算法顯著優于FFT法、最高電壓法、最大Δf法。其中，高維三迭代算法的定位范圍高于FFT法約為6.67 km，準確性高于最大Δf法約為8.67%，相對誤差小于最高電壓法約為0.05%。由此說明，高維三迭代算法具備FFT法、最高電壓法、最大Δf法三種方法的優點。進一步驗證，對上述方法進行二維故障判斷，結果如表2所示[8-11]。

表2 二維的故障判斷分析

由表2分析可知，準確性、結果相對誤差、故障的定位范圍等方面，高維三迭代算法優于FFT法、最高電壓法、最大Δf法，而且優化結果與表1基本一致，說明高維三迭代算法的計算結果并不會因為維度的變化而變化。而且，兩個維度之間的計算結果比較穩定，諸如，準確性為96.67%、96.31%，相對誤差為0.22%、0.21%，未出現顯著性的改變。為了更加準確地進行高維三迭代算法的驗證，要對高維輸電線路故障的定位時間進行分析，結果如表3所示。

表3 二維輸電線路故障的定位時間

由表3分析可知，電壓、定位時間、定位范圍、相對誤差等方面，高維三迭代算法優于FFT法、最高電壓法、最大Δf法。其中，高維三迭代算法的二維輸電線路的定位時間小于最大Δf法17～20 s。而且，兩個維度的計算時間穩定，時間差僅為1.36 s。另外，高維三迭代算法的相對誤差為0.11%、0.12%，小于FFT法的0.26%、0.12%。

4 結 論

本文針對輸電線路故障定位的問題，提出一種高維三迭代算法,充分考慮相鄰頻率、計算距離、故障距離的判斷范圍、相對誤差對故障的影響問題。對500 kV進行案例分析，結果顯示，高維三迭代算法的準確率、計算時間、故障定位范圍、相對誤差優于最高電壓、FFT、最大Δf法等算法，說明高維三迭代算法可以提高500 kV輸電線路故障的定位準確性，而且計算時間較短。