基于前景理論的多災點應急人員調度研究

劉康儒，朱昌鋒*，王慶榮，張志偉，馬 斌

（1.蘭州交通大學 交通運輸學院，蘭州 730070；2.蘭州交通大學 電子與信息工程學院，蘭州 730070）

大規模突發事件初期，應急人員調度作為應急救援中最關鍵的環節之一，將直接影響到應急救援效率.因此，如何科學合理地調度應急人員是一個極具現實意義的課題.

國內外學者對應急人員調度問題已開展了一定的研究.文獻［1-4］通過考慮救援時間不確定等災情特征，以救援時間效用、救援效果和救援可靠性等為目標，構建了應急人員調度多目標優化模型.Rauchecker等［5］通過考慮救援單位間的協作，將救援單位調度描述為一個二元線性最小化問題.Chen等［6］從雙邊匹配的角度研究了志愿者派遣問題，提出了一種基于證據推理的方法來解決志愿者隊伍與救援任務間的不確定匹配關系.然而，上述研究均未涉及多出救點-多受災點-多應急任務下的應急人員調度問題，與現實存在偏差.針對上述不足，相關學者開始研究多受災點背景下的應急人員調度問題.Zhang等［7］通過考慮救援隊伍特征，構建了多階段動態響應災害鏈條件下的應急人員調度模型及算法.Li等［8］通過綜合考慮應急人員的主觀偏好和客觀能力，構建了多受災點背景下的應急人員調度模型.以上研究主要從時間效用和救援效果兩個角度研究應急人員調度問題，但均以假設災民和應急人員完全理性為前提.事實上，由于不完全不對稱信息和不完美的判斷能力的限制，災民和應急人員對救援方案的心理感知是有限理性的.前景理論（prospect theory，PT）通過考慮現實中人的參照依賴和風險偏好等特征，真實描述了決策者的有限理性行為.文獻［9-11］通過引入PT，刻畫了有限理性條件下災民對救援時間和需求滿足率的心理感知.然而，上述研究均未考慮有限理性條件下應急人員對應急任務的心理感知.

基于上述分析，本文聚焦多受災點下的應急人員調度問題，通過考慮災民對救援到達時間和應急人員對應急任務的有限理性心理感知，構建以最大化時間滿意度和任務勝任度為目標的應急人員調度多目標優化模型，并設計相應的第二代非支配排序的遺傳算法（non-dominated sorting genetic algorithm II，NSGA-II）對模型進行求解.最后，通過算例求解與分析驗證了本文模型和算法的合理性和有效性.

1 問題描述

假設某地發生大規模突發事件，受災點和出救點集合分別為D=｛Dk｜k=1，2，…，n｝和A=｛Ai｜i=1，2，…，m｝．受災點Dk的災情嚴重程度為ρk，ρk越大，災情越嚴重，0＜ρk≤1且．出救點Ai的應急小組數量為ai，出救點Ai的第j個應急小組為Pij．

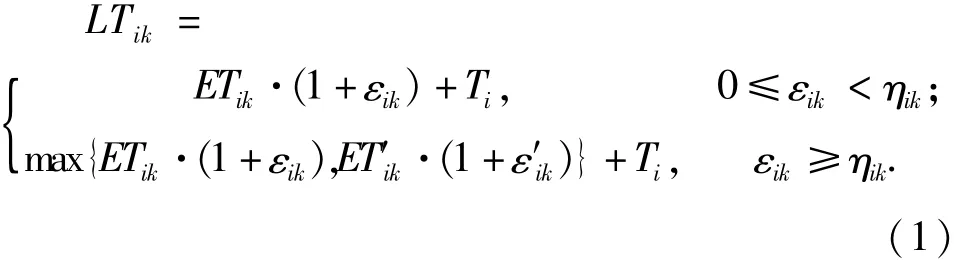
考慮到路況和天氣等因素對救援到達時間的影響，將到達時間刻畫為區間［ETik，LTik］．ETik為最短路徑的理想到達時間，LTik為考慮路況、應急小組整備時間和更換路徑條件下的最晚到達時間，即：其中：Ti為出救點Ai中應急小組的整備時間；εik為路況等因素對最短路徑理想到達時間的影響系數，εik≥0；ET′ik為Ai至Dk備選路徑的理想到達時間；ε′ik為路況等因素對備選路徑理想到達時間的影響系數，ε′ik≥0；ηik為路徑選擇閾值．

對任務勝任度的衡量需綜合考慮應急人員主觀滿意度和客觀能力［8］．應急任務集合為TA=｛TAc｜c=1，2，…，C｝，受災點Dk待完成任務的數量為Lk，Lk≤C．在主觀滿意度方面，應急小組Pij對應急任務TAc存在偏好序越小，應急小組Pij完成應急任務TAc的意愿越強，特別地表示Pij對應急任務TAc無意愿．在客觀能力評價方面，應急任務TAc的能力指標權重集合為表示應急任務TAc關于第h個指標的權重且．出救點Ai中應急小組能力指標評價矩陣為為應急小組Pij的第h個能力指標的評價值的值以評分的形式給出，如0至10分．

xijk∈｛0，1｝表示應急小組Pij是否被派往受災點Dk，為決策變量表示應急小組Pij是否被派往受災點Dk完成任務TAc，為決策變量．

2 模型構建

2.1 有限理性下的時間滿意度和任務勝任度

累積前景理論（cumulative prospect theory，CPT）是對PT的完善，其通過使用累積的而不是單獨的決策權重，彌補了PT不滿足隨機占優和不適用于結果任意多的風險前景的缺陷.CPT主要通過價值函數和權重函數評價某一風險結果的價值.

2.1.1 時間滿意度

對于不確定且結果任意多的到達時間，本文采用CPT刻畫災民對應急小組到達時間的滿意度.時間滿意度的價值函數如式（2）所示，價值函數曲線如圖1所示.價值函數反映了有限理性下的災民對時間價值的感知是基于參照點的，面對增益會規避風險，面對損失會追求風險，且對損失更敏感的心理.

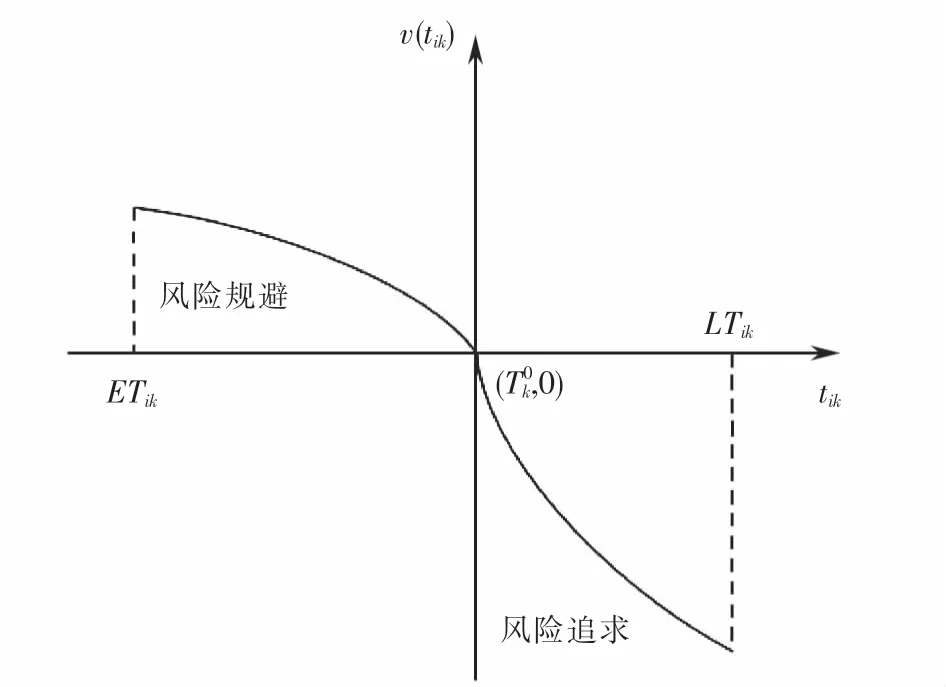
圖1 時間滿意度的價值函數曲線Fig．1 Value function curve of time satisfaction

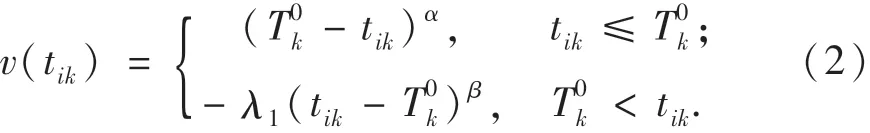
其中：α為風險規避參數，0＜α≤1；β為風險追求參數，0＜β≤1；λ1為災民的損失規避系數，λ1≥1，根據既有研究的標定，α=β=0．88，λ1=2．25［12-14］；tik為出救點Ai中應急小組至受災點Dk的實際到達時間，可取［ETik，LTik］中的任意時刻；T0k為受災點Dk中災民對救援到達時間的參照點，即：

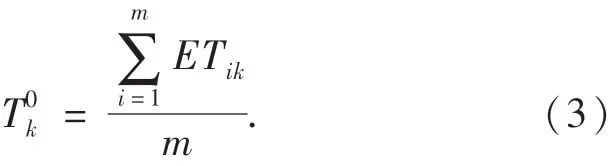
記pik是與tik對應的概率，災民感知收益和損失時的決策權重函數如式（4）所示，決策權重函數曲線如圖2所示.決策權重函數反映了有限理性條件下的災民會迷戀小概率事件的心理.

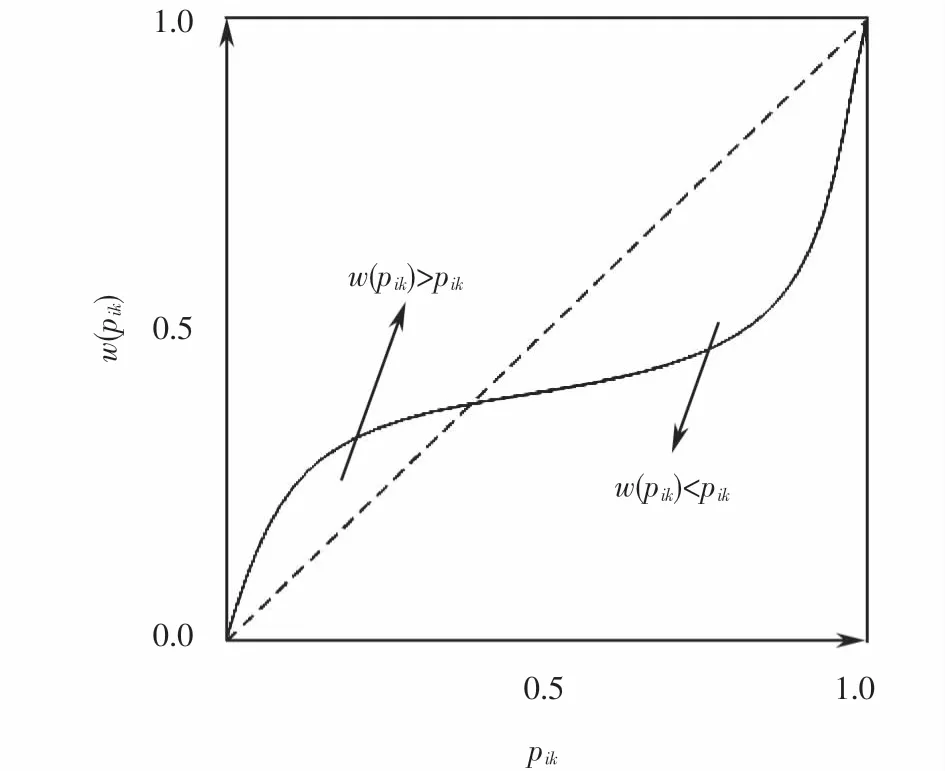
圖2 時間滿意度的決策權重函數曲線Fig．2 Decision weight function curve of time satisfaction

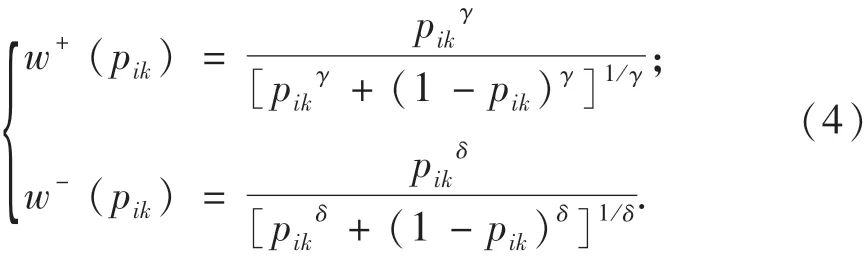
其中：γ為獲得感知概率參數，γ＞0；δ為損失感知概率參數，δ＞0．根據既有研究的標定，γ=0．61，δ=0．69［12-14］．

假設有M+N+1種可能的到達時間，將連續的到達時間區間［ETik，LTik］離散化為K段為第g段中值對應的概率［12-13］，則災民感知收益和損失時的累積權重函數為

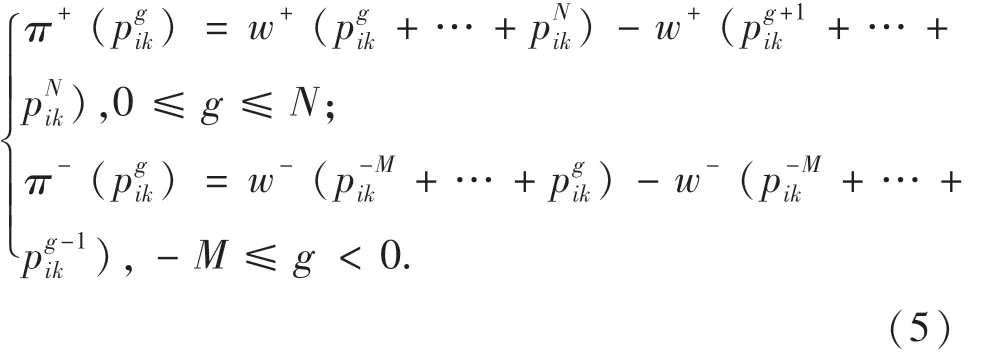
在價值函數和累積權重函數的基礎上，災民對應急小組Pij調往Dk的時間滿意度為

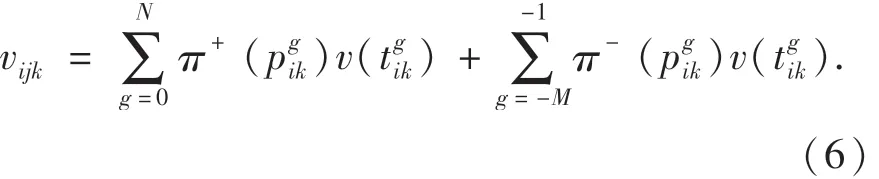
2．1．2 任務勝任度

任務勝任度是應急小組主觀滿意度和客觀能力的結合［8］．對于不同的應急任務，應急小組主觀滿意度的變化并非是線性的，且應急小組會對應急任務存在有限理性的心理感知．因此，基于應急小組對應急任務的偏好序，本文采用CPT的價值函數刻畫應急小組Pij對應急任務TAc的主觀滿意度S（rc ij），即：

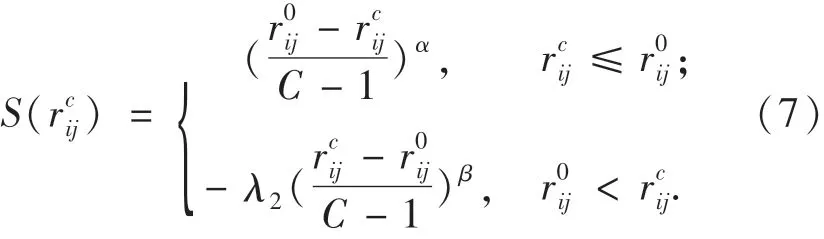
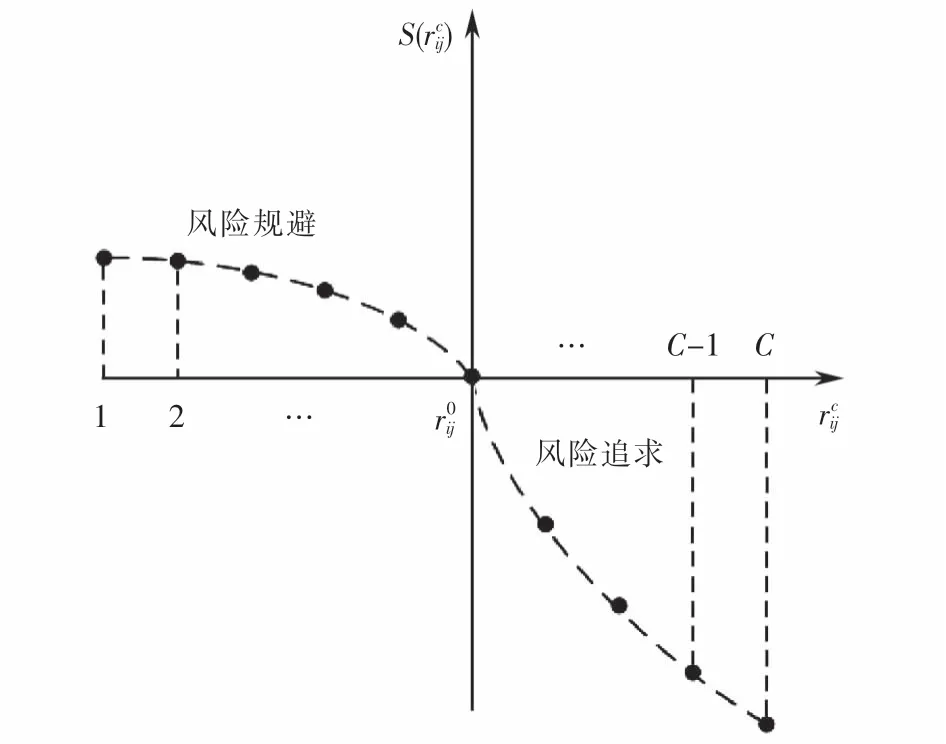
圖3 應急小組主觀滿意度函數曲線Fig．3 Subjective satisfaction function curve of emergency team

在應急小組主觀滿意度和客觀能力的基礎上，采用幾何平均算子得出Pij完成任務TAc的勝任度即：

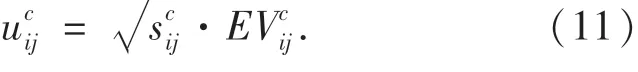
2．2 應急人員調度模型構建

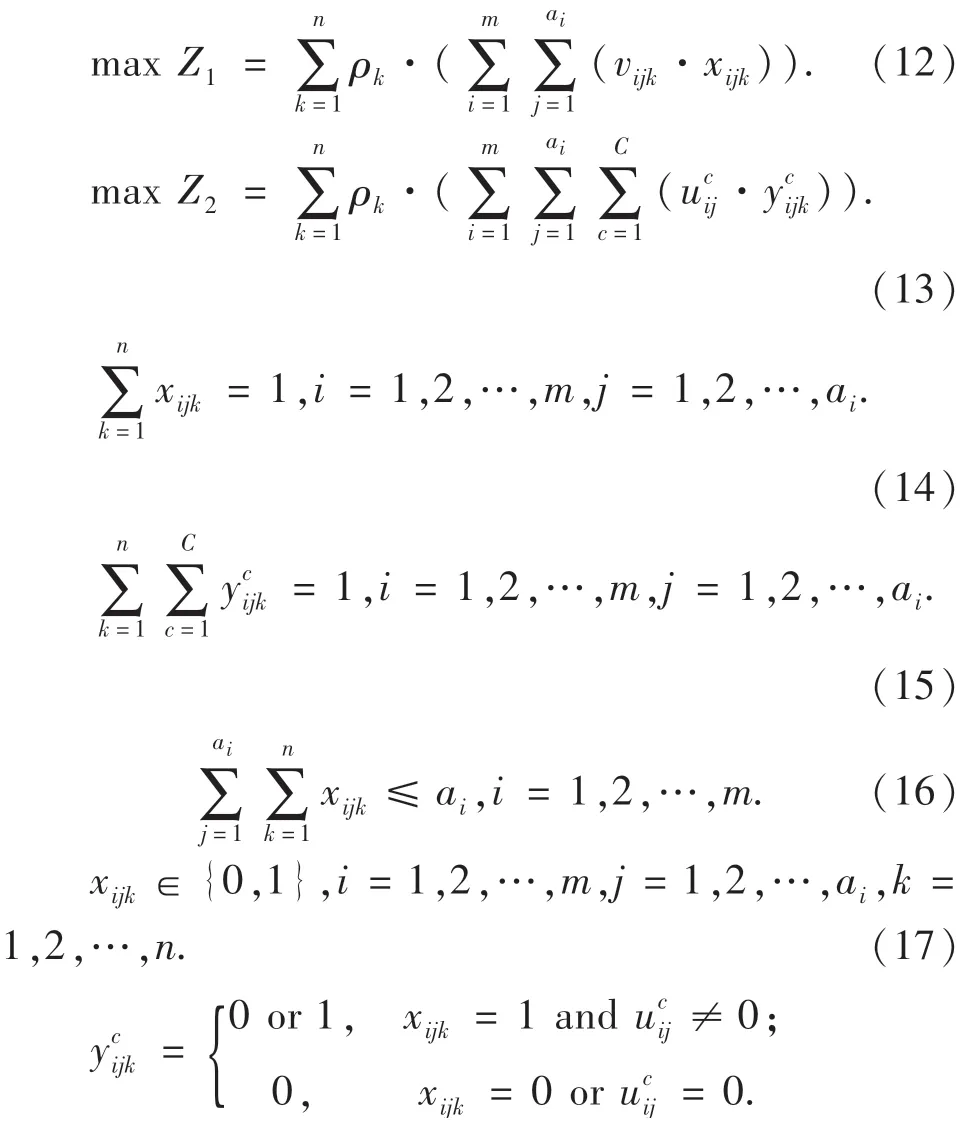
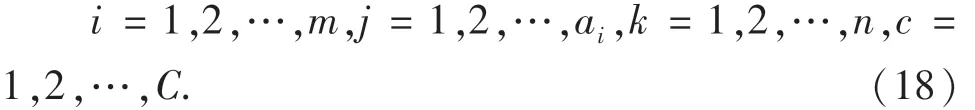
基于2．1節內容，結合應急人員調度實際，有限理性條件下考慮多受災點的應急人員調度模型如下：其中：式（12）和（13）分別為時間滿意度和任務勝任度目標函數；式（14）表示一個應急小組只能去往一個受災點；式（15）表示一個應急小組只能完成一項應急任務；式（16）為出救點Ai中應急小組的數量約束；式（17）和（18）為決策變量取值約束．

3 算法設計

3.1 勝任度求解策略

通過分析式（12）～（18）可發現，受災點Dk的任務勝任度的計算是一個以效益最大為目標的廣義最優指派問題．對此，匈牙利算法可在多項式時間內求解該類問題，且應用廣泛．另外，根據總應急小組數與總應急任務數間的不確定關系，應急人員調度存在三種情景.基于上述分析，本文在匈牙利算法的基礎上，提出了一種適應不同應急人員調度情景的任務勝任度求解策略，如表1所列.

表1 勝任度求解策略Tab．1 Competency solving strategy

3.2 多目標優化算法設計

在所建模型和勝任度求解策略的基礎上，應急小組調度方案的確定具有明顯的并行性，遺傳算法的群體適應度評價和隨機搜索等特征使其具備求解該類問題的優勢［15-16］.對于多目標優化，NSGA-II算法在繼承遺傳算法的全局并行搜索優勢的同時，通過提出快速非支配排序算子、擁擠比較算子和精英策略提高了Pareto前沿的精確性、均勻性和收斂性［17-18］.本文采用NSGA-II算法對應急小組調度模型進行求解，下面是NSGA-II算法的關鍵操作.

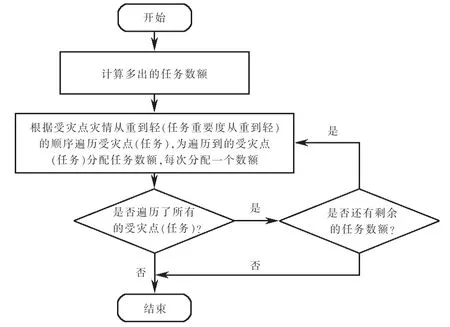
圖4 任務數額增加方法Fig．4 Method of increasing the number of tasks

1）染色體編碼

分析式（12）～（18）和勝任度求解策略可知，僅有決策變量xijk參與染色體編碼，故染色體編碼采用二進制編碼．整條染色體可劃分為個基因片段，每個片段的基因位數等于受災點數n．具體地，某一基因片段的第k個基因位的值表示：若該基因片段所指的應急小組被派往受災點Dk，則該基因片段第k個基因位的值為1，否則為0．染色體長度為，染色體編碼示意圖如圖5所示.

圖5 二進制編碼染色體Fig．5 The binary coded chromosome

2）約束處理方式及適應度函數的確定

在勝任度求解策略的基礎上，考慮到模型約束的復雜性不強，故將約束（14）～（18）直接加入到新個體的生成過程中，如個體初始化，交叉和變異等操作.另外，采用目標函數作為適應度函數，即：

3）交叉，變異算子

基于圖5所示二進制編碼染色體，本文采用單點交叉和單點變異算子.其中，交叉算子的交叉位置指向兩個相鄰基因片段的連接處，變異算子的變異位置指向任一基因片段.以三個受災點，三個出救點，每個出救點中有一個應急小組為例，交叉和變異算子分別如圖6～7所示.

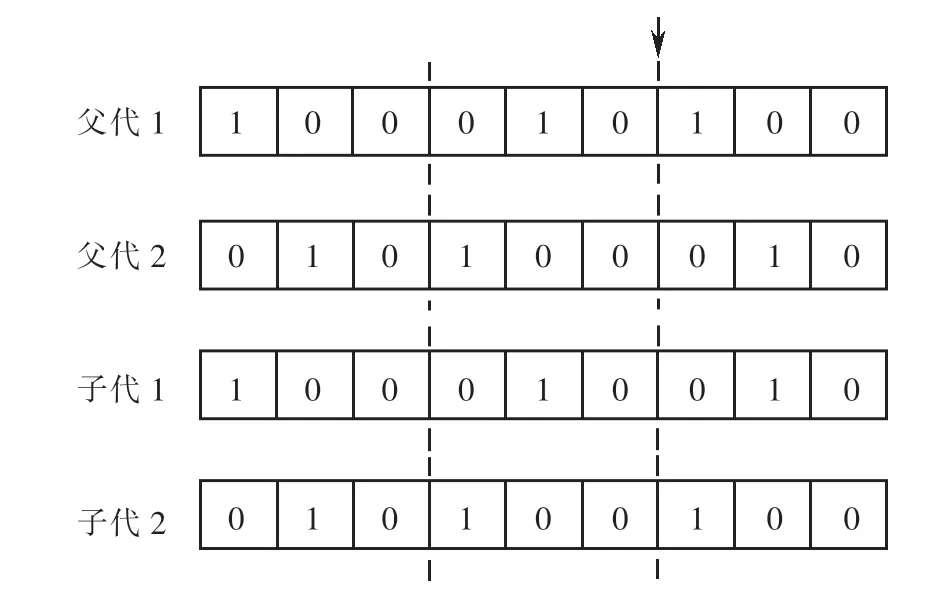
圖6 交叉算子Fig．6 Crossover operator

在確定算法關鍵操作的基礎上，算法流程如圖8所示.

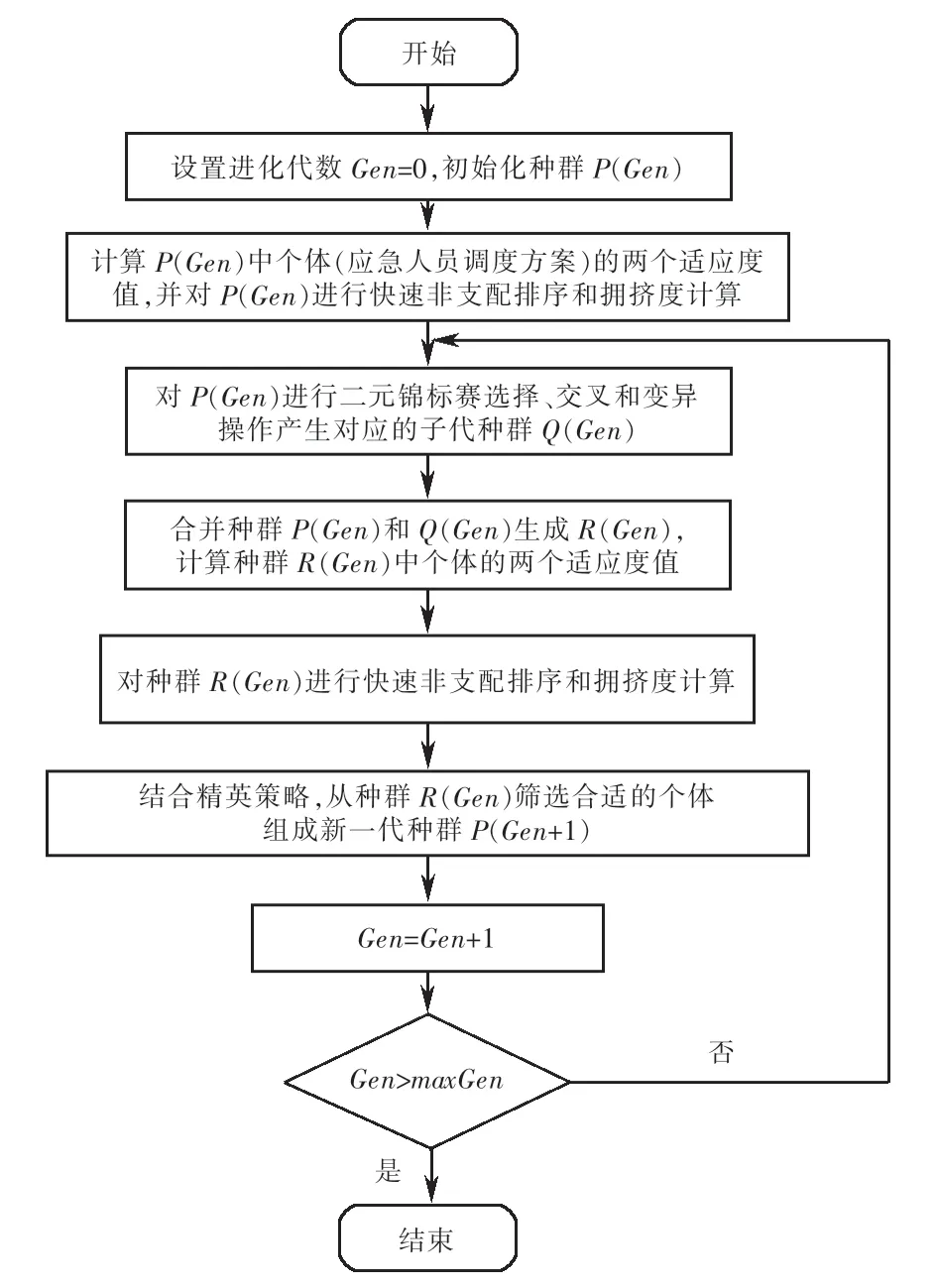
圖8 NSGA-II算法流程Fig．8 NSGA-II algorithm flow

Pareto前沿解集在提供多個可選方案的同時，也為決策者做出最終決策帶來了困難.在決策者沒有明顯偏好且應急決策時間緊迫的情況下，給出理想解篩選方法是有必要的.結合本研究內容，本文采用文獻［7］中的理想解篩選方法.

4 算例分析

4.1 算例背景

考慮到三種勝任度求解策略的應用情景最終都可轉化為情景Ⅱ，因此，為驗證模型和算法的合理性，本文在情景Ⅱ的基礎上設計算例，并對其進行求解與討論分析.

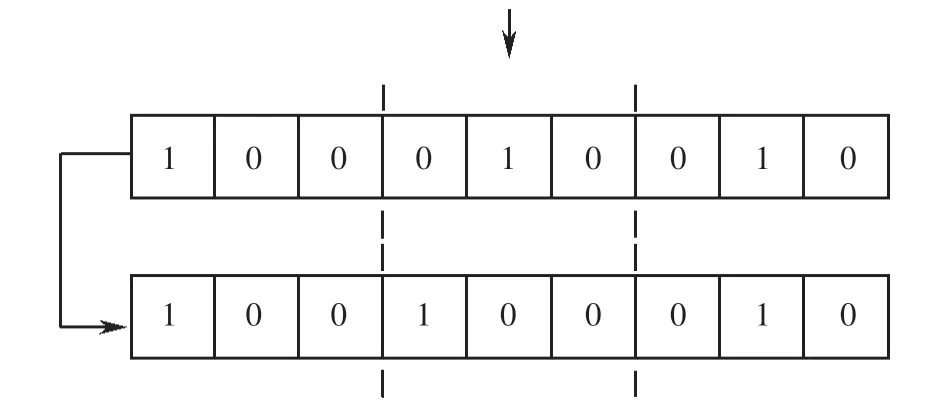
圖7 變異算子Fig．7 Mutation operator

算例由4個受災點，5個出救點和5類應急任務構成.各災點災情嚴重程度分別為ρ1=0．35，ρ2=0．2，ρ3=0．2，ρ4=0．25．各出救點中應急小組數量分別為a1=3，a2=2，a3=4，a4=3，a5=4，依照出救點的順序，各應急小組的任務偏好參照點為｛3，3，4，4，3，3，3，2，2，3，3，3，3，3，4，4｝．應急小組能力評價指標共7項．各出救點應急小組整備時間分別為T1=1，T2=1．5，T3=2，T4=1．5，T5=1.5.各受災點的最短路徑理想到達時間如表2所列；路況等因素對最短路徑理想到達時間的影響系數如表3所列；各受災點的應急任務如表4所列；應急任務指標權重如表5所列；應急小組對應急任務的偏好序如表6所列；應急小組能力指標評價值如表7所列.

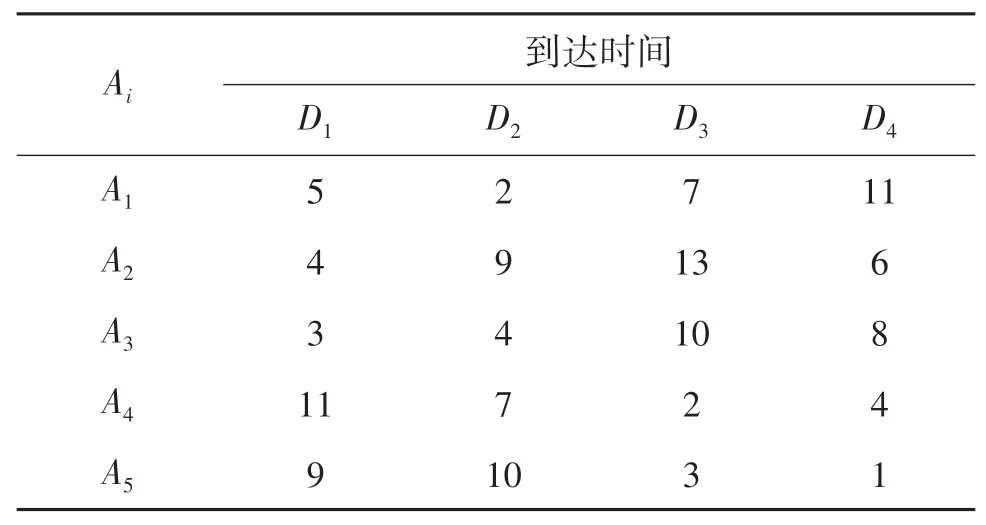
表2 理想到達時間Tab．2 Ideal arrival time h

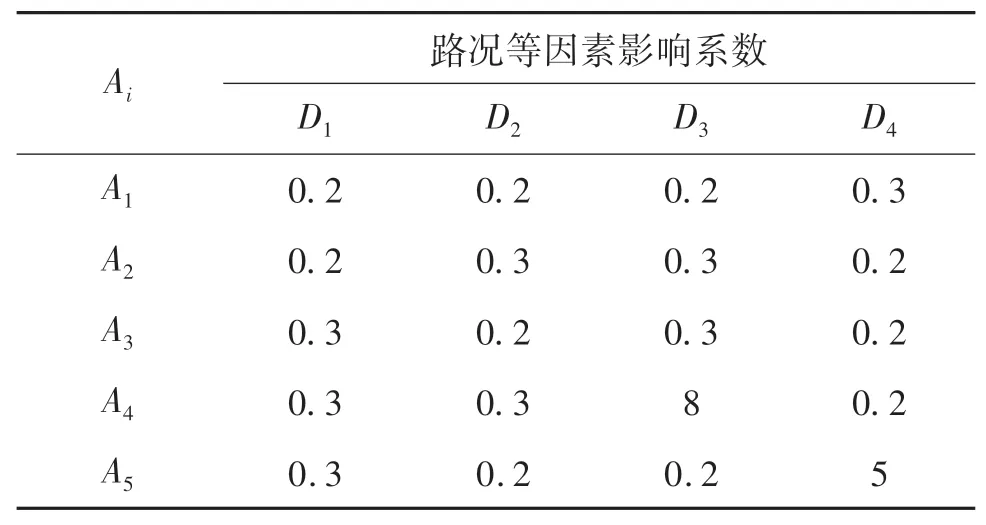
表3 路況等因素對理想到達時間的影響系數Tab．3 Influence coefficient of road conditions and other factors on ideal arrival time

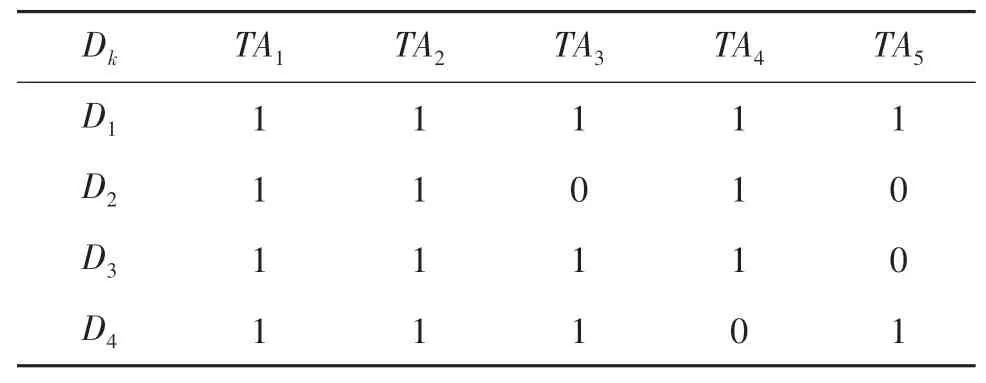
表4 各受災點待完成的應急任務Tab．4 Emergency tasks at each disaster area

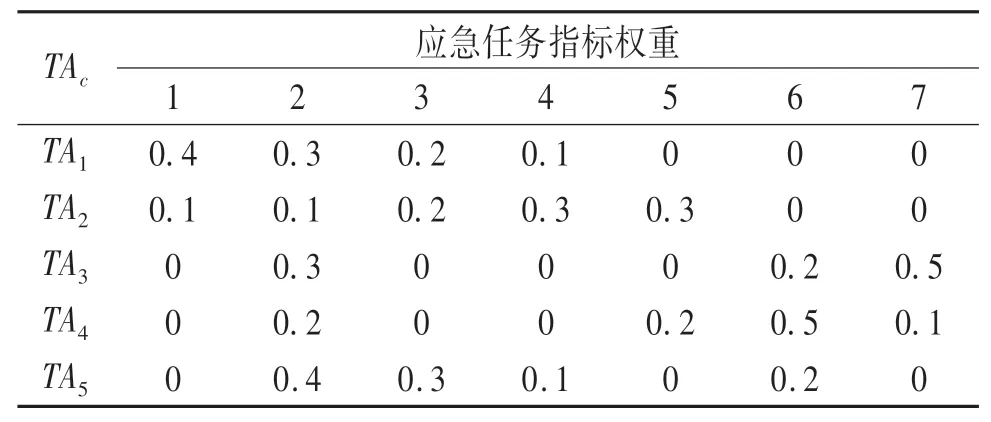
表5 應急任務指標權重Tab．5 Emergency task indicator weight

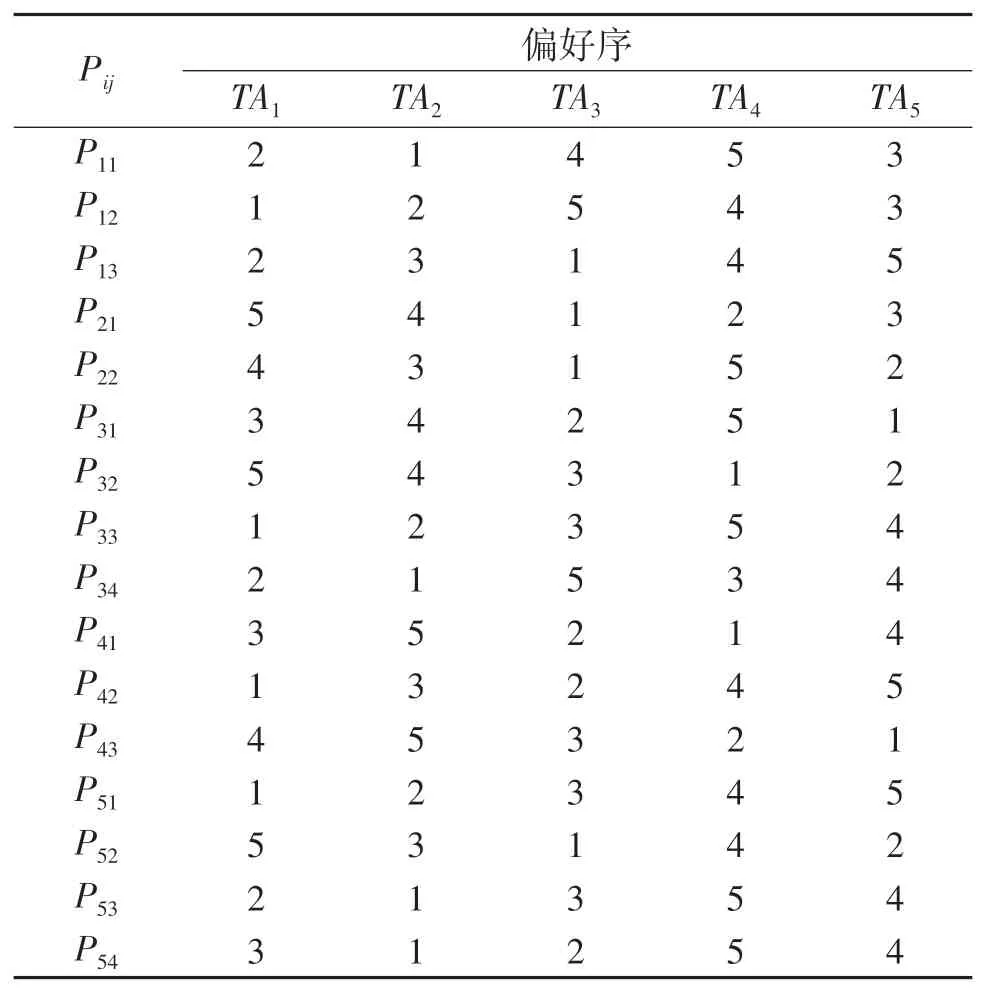
表6 應急小組偏好序Tab．6 Emergency team preference

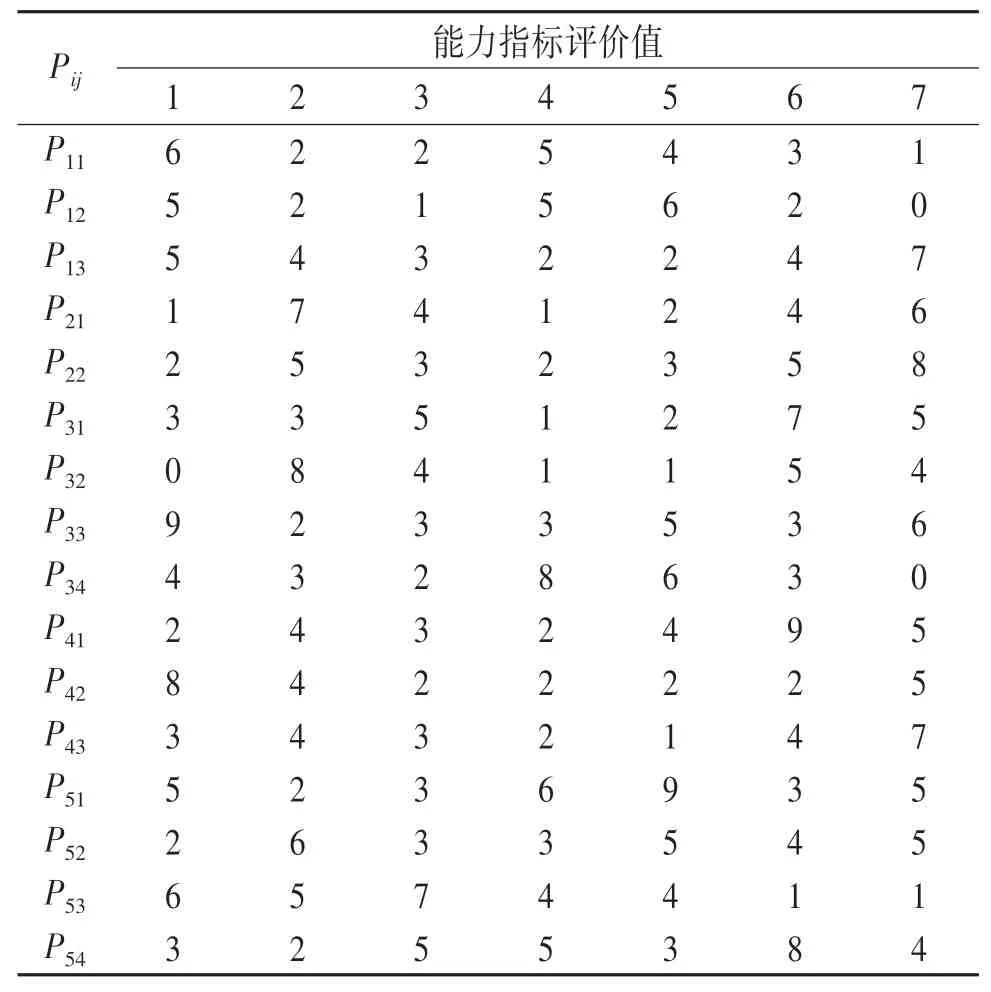
表7 應急小組能力指標評價值Tab．7 Evaluation value of emergency team capability index分

基于給定的基礎數據，應急小組對各項應急任務的勝任度如表8所列.

表8 應急小組任務勝任度Tab．8 Emergency team task competence

4.2 算例求解與分析

本文基于VisualStudio2017開發環境，采用C++編程語言實現算法并求解算例.在算法方面，設置種群規模為100，迭代次數maxGen為500次，交叉概率pc為0．9，變異概率pm為0．02．在模型參數方面，設置λ1=λ2=2.25.Pareto前沿解數的迭代曲線如圖9所示.

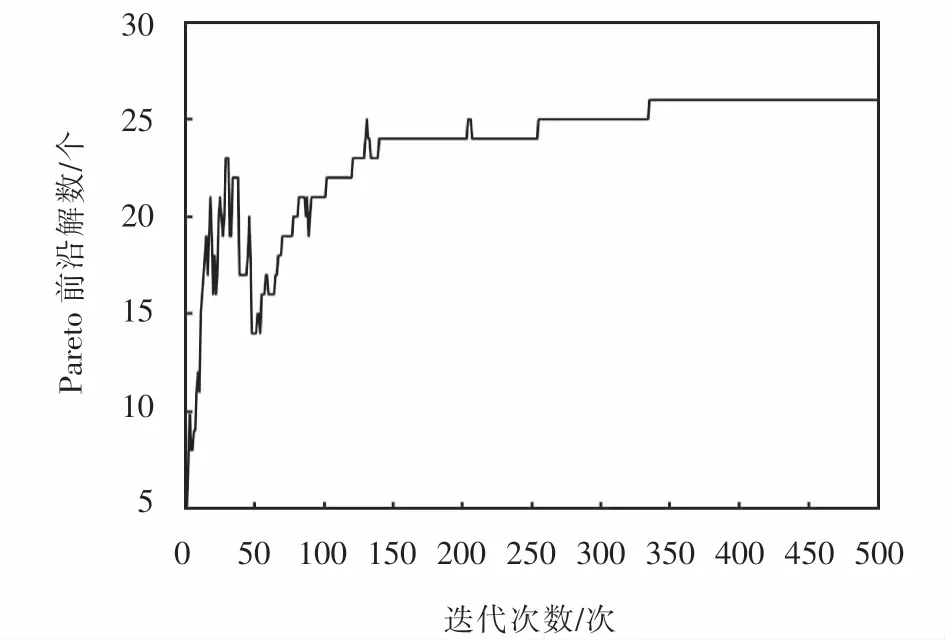
圖9 Pareto前沿解數的迭代曲線Fig．9 Number iteration curve of Pareto frontier solutions

由圖9可見，當算法迭代350次左右時，Pareto前沿解的數量收斂到26個.為進一步驗證迭代350次的Pareto前沿已經收斂，將迭代350次和500次的Pareto前沿進行對比，如圖10所示.

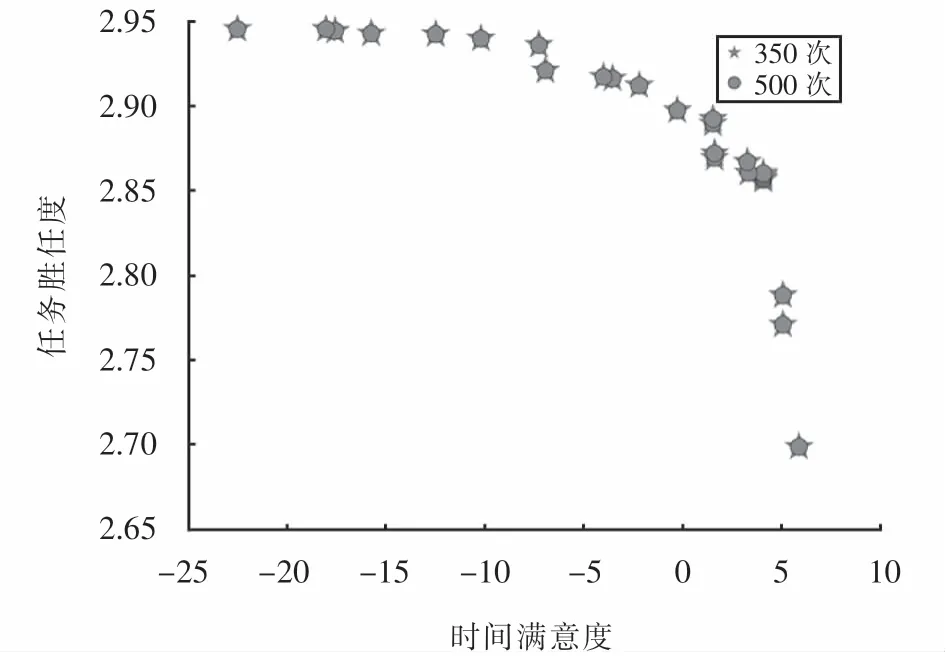
圖10 迭代350次與500次的Pareto前沿Fig．10 Pareto frontier with 350 and 500 iterations

由圖10可以看出，一方面，迭代350次和500次的Pareto前沿基本一致，這表明迭代350次的Pareto前沿已經收斂.基于以上分析可得，針對多受災點條件下的應急人員調度問題，設計的NSGA-II算法是有效的，可快速準確地收斂.另一方面，時間滿意度和任務勝任度間存在負相關關系：隨著救援時間的增加，任務勝任度先快速增加后趨于穩定，這是目標間的沖突造成的.

取迭代350次的Pareto前沿解集做進一步的分析，選擇時間滿意度最優解（方案1）、理想解（方案2）和任務勝任度最優解（方案3）作為研究對象.三個特殊解對應的目標函數值和具體調度方案如表9～10所列.

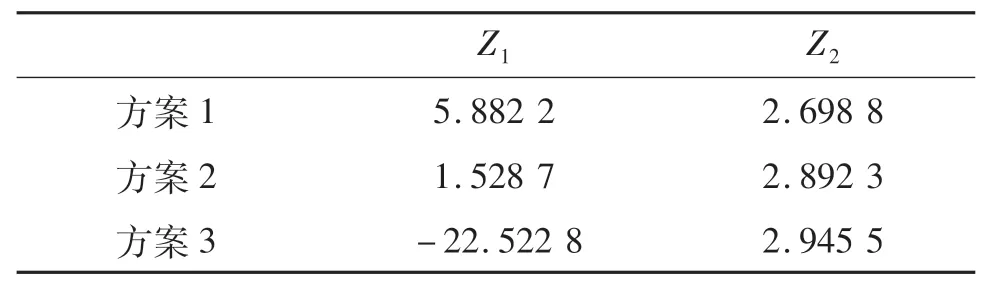
表9 三個特殊解的目標函數值Tab．9 Objective function values for three special solutions

首先，綜合表2、表3和表10可以看出，在方案2中，A4和A5中部分應急小組被派往因嚴重受路況等因素影響而在到達時間上明顯劣勢的受災點.這說明，嚴重受路況等因素影響的理想到達時間較短的路徑已成為制約救援效果提升的瓶頸，決策者須予以重視.其次，記應急小組勝任度最高的任務為1級任務，次高任務為2級任務，以此類推.為了驗證勝任度求解策略的合理性，我們給出了應急小組完成不同勝任度等級任務的數量分布，如圖11所示.

由圖11可以看出，方案2與方案3在任務分配效果上差異較小，方案1與另外兩個方案的任務分配效果差異較大.然而，結合表8和表10可發現，三個方案中各受災點的任務分配都是基于當前所得應急小組的最優分配.這說明，在所建模型的基礎上，勝任度求解策略兼顧了模型求解優化和高質量的任務分配.最后，考慮到應急救援初期的時間緊迫性，結合圖10，本文推薦在時間滿意度處于［1.528 7，5.882 2］的調度方案中選擇最優方案.

表10 三個特殊解的具體調度方案Tab．10 Specific scheduling schemes for three special solutions

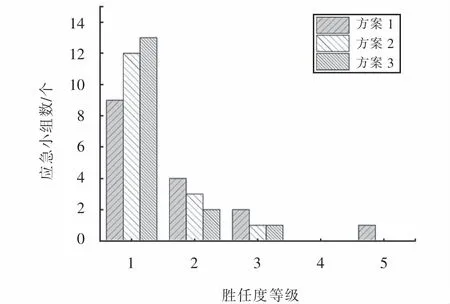
圖11 不同勝任度等級下的小組數分布Fig．11 Distribution of team numbers under different competency levels

4.3 前景理論參數分析

4.3.1 時間滿意度參數分析

時間滿意度主要會受到風險態度參數α，β和感知概率參數γ，δ的影響．為分析時間滿意度對α，β，γ，δ的靈敏度，以三個方案的時間滿意度為研究對象進行分析，如圖12所示.

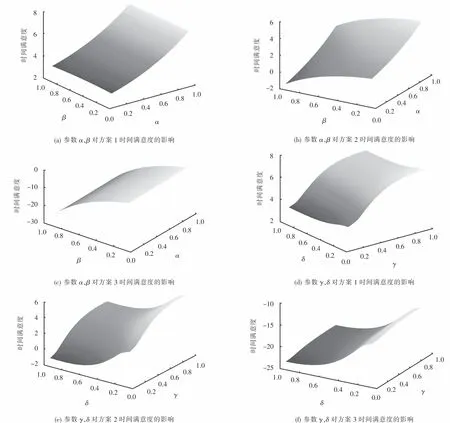
圖12 參數α，β，γ，δ對三個方案的時間滿意度的影響Fig．12 The influence of parametersα，β，γ，δon the time satisfaction of the three schemes

由圖12（a），12（b），12（c）可看出：時間滿意度與α呈正相關，與β呈負相關；方案1的時間滿意度對α的敏感度遠大于β，方案2的時間滿意度對α和β的敏感度相當，方案3的時間滿意度對β的敏感度遠大于α．考慮到三個方案下的災民對救援時間的感知分別為高增益、混合低增益和高損失，上述現象表明：當救援時間整體早于災民預期時，災民更傾向于為保留當前增益而規避風險；當救援時間整體晚于災民預期時，災民更傾向于追求增益而規避風險；當救援時間整體略早于災民預期時，災民在有規避風險傾向的同時，也會存在為追求更大增益而追求風險的傾向．這有助于促進方案的優化調整．另外，整體來看，時間滿意度對β的敏感度更強，這符合獲取信息有限（對救援到達時間的不確定性考慮不足）的災民會對救援時間有過高期望且對損失更敏感的現實.

由圖12（d），12（e），12（f）可看出：時間滿意度與γ呈正相關，與δ呈負相關；方案1的時間滿意度對γ的敏感度遠大于δ，方案2的時間滿意度對γ和δ的敏感度相近，方案3的時間滿意度對δ的敏感度遠大于γ。這是因為，γ越大，災民越傾向于感知方案在時間上較優，故方案1和方案2中處于增益狀態的災民的時間滿意度越大，方案3的災民處于高損失狀態，故幾乎不受γ的影響．對δ的分析與γ類似．另外，整體來看，時間滿意度受δ的影響更大，這說明災民會對方案無效更敏感.

4.3.2 任務勝任度參數分析

任務勝任度主要會受到風險態度參數α，β的影響．我們以三個方案的任務勝任度為研究對象，分析其對風險態度參數α，β的靈敏度，如圖13所示.

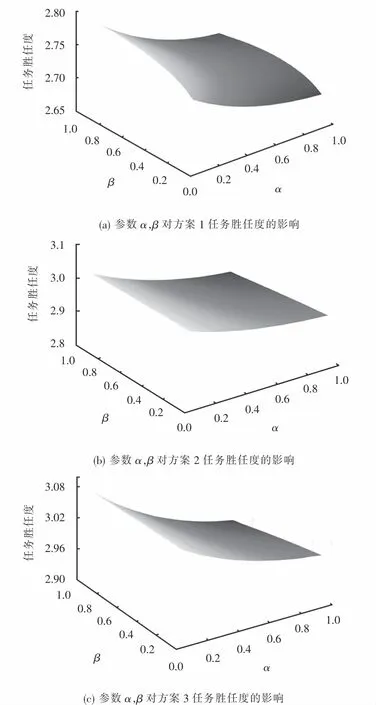
圖13 參數α和β對三個方案的任務勝任度的影響Fig．13 Influence of parametersαandβon task competency of three schemes

由圖13可看出：任務勝任度在整體上與α呈負相關，與β呈正相關；三個方案均對α更敏感.這說明三個方案在任務勝任度上均是較優的，故任務偏好得到滿足的應急人員會更傾向于為保留當前增益而規避風險.同時，該現象符合在救援時間緊迫的背景下，應急人員會對任務偏好序期望較低的現實.

5 結論

1）構建的多目標優化模型結合勝任度求解策略，可得到一系列Pareto前沿解供決策者依據具體災情選擇，可為多受災點下的應急人員調度及相關研究提供參考.

2）設計的NSGA-II算法可快速、準確地求出Pareto前沿，是解決本文目標問題的有效手段.

3）引入前景理論刻畫的時間滿意度和任務勝任度，真實地反映了應急救援中災民和應急人員的心理感知，有效彌補了既有研究完全理性人假設的不足.

4）考慮災情動態性和應急小組的不完全偏好序是下一步研究重點.