面向六自由度移動機械手底座位置優化方法

馬金茹，高文華，祁宇明

(1.北京電子科技職業學院汽車工程學院，北京100176；2.天津科技大學，天津 300222;3.天津職業技術師范大學，天津 300222)

0 前言

隨著機器人技術的快速發展，移動機械手由于具有良好的機動性和靈活性，可以靈活地到達不同的工作位置，完成復雜的加工任務，在大型復雜零件的加工中具有廣闊的應用前景。然而機器人在任務空間中的性能分布是高度非線性的，這使得確定最合適的基座位置 (BP)非常困難。因此有必要建立一種有效的移動機械手BP優化方法，快速準確地確定最優BP，這對裝配成本的降低具有重要意義。

移動機械手基座優化能夠有效提高任務的完成效率和質量，受到了眾多研究者的關注。為了實現更高的生產效率，面向任務的目標函數被應用于機器人基座優化問題，如最短路徑和最小循環時間、最低能耗。在大多數情況下，基座位置優化關注的是提高任務的完成質量，這與機器人的性能密切相關。因此，現有的許多方法主要是為了提高機器人的性能，蔣毅等人研究了某四自由度機器人基座優化方法，通過有限元軟件對機器人結構進行仿真，分析了機器人結構參數對機器人動態特性的影響，在此基礎上以基座基頻為優化目標確定了最優基座位置。張崇等人研究了風電塔筒機器人電機基座優化問題，建立了以電機基座的動態載荷為目標的有限元拓撲方法，確定了電機基座輕量化目標的最佳位置。REN等提出了優化移動機械手基礎位置的算法，該算法考慮到機械手的物理限制和奇異性，通過實驗驗證了該算法的優越性。YU等針對移動涂裝機器人，建立近似解耦模型，在此基礎上提出了機械手底座位置優化方法，考慮了定位約束、定向約束和奇異回避約束，將BP優化問題轉化為路徑準則的標準不等式約束優化問題，通過實驗驗證了所提方法的有效性。

以上主要方法為機器人系統的底座位置(BP)優化提供了重要參考，但基本上都是關注機器人的運動能力和運動性能，很少考慮機器人的剛度性能。鑒于機器人的剛度性能通常對加工質量有一定的影響，作者提出一種同時考慮機器人運動學和剛度性能的底座位置BP優化方法，以最大全局剛度性能評價指標為目標函數，以關節距離、關節速度、奇異避免和碰撞避免為約束條件，建立優化模型，采用稀疏均勻網格分解尋找優化模型的有效初值，通過序列二次規劃(SQP)方法最終求解基座的最優位置。

1 運動學和剛度性能指標

設計合適的性能評價指標是移動機械手BP優化的前提。以六自由度機器人為例，分別介紹用于BP優化的動力學和剛度性能指標。D-H參數模型和數據分別如圖1和表1所示，=0.3 m,=0.7 m,=0.28 m,=0.893 m,=0.2 m。

圖1 D-H參數模型

表1 機器人的D-H參數

1.1 運動性能指標

雅可比矩陣的條件數是評價運動學性能的有效方法。將采用基于Frobenius范數的運動學雅可比矩陣的條件數()作為量化奇點距離的方法，該指數稱為動靜調節指數(KCI)，定義為

(1)

其中：tr(·)為矩陣的跡；為具有相同物理單位的齊次雅可比矩陣，定義為

(2)

其中：、、分別為3×3的單位矩陣、3×3的零矩陣和雅可比矩陣;為特征長度，可通過求解的最大值得到。的取值范圍為(0,1]，值越高，機器人的運動學性能越好，特別是當=1時，雅可比矩陣的所有奇異值都相等，說明該機器人具有最佳的運動學性能。反之，當=0時，雅可比矩陣的最小奇異值趨近于零或最大奇異值趨近于無窮大，機器人的運動性能將惡化。

1.2 剛度性能指標

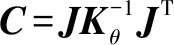
(3)

其中：diag(·)為對角化函數；(=1,2,…,6)為第個關節剛度值(N·m/rad)，可通過有限元分析方法得到。對于六自由度機器人，關節剛度矩陣為

=diag([2.03×106.02×101.91×10

0.45×100.22×100.07×10])

(4)

根據柔度模型，端部執行器(EE)的位移與施加在其上的扳手關系可以定義為

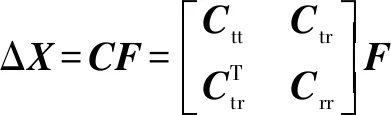
(5)

其中:是柔度矩陣，即的逆；Δ是由EE的平移和轉動位移組成的6×1位移矢量；是施加在EE上的力和力矩組成的6×1扳手矢量。、、分別為3×3平移子矩陣、耦合子矩陣和轉動子矩陣，其單位分別為m/N、rad/(N·m)和rad/N。此外，考慮到在加工過程中，可忽略刀具的轉動位移、平移位移和作用在刀具上的扭矩，則可將式(5)重新定義為

Δ=

(6)

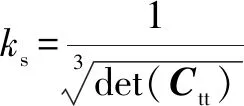
(7)

指標可以很好地表征機器人在一定關節角度下的剛度性能，的值越大，機器人的剛度性能越好。但僅為局部性能指標，不能直接用于評價機器人在加工任務中的全局剛度性能。基于此，提出了一種面向任務的全局剛度性能評價指標，其定義為

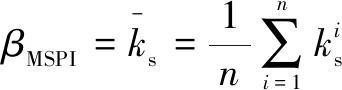
(8)

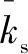
2 優化問題

BP優化的目標是在保證機器人運動學性能的前提下，盡可能地提高機器人的剛度性能。圖2所示為移動機械手加工系統模型。

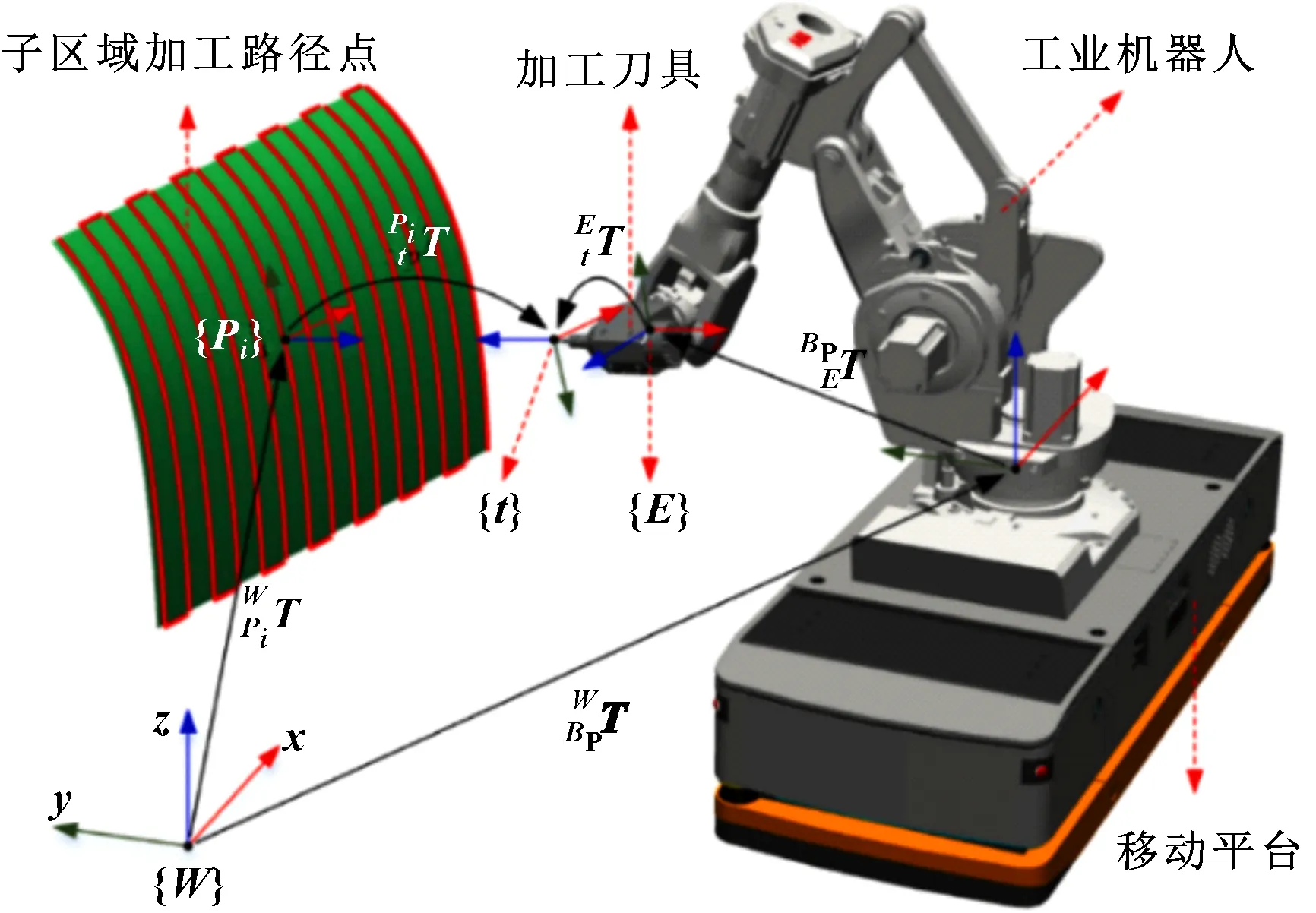
圖2 移動機械手加工系統

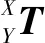
(9)

其中:=×。

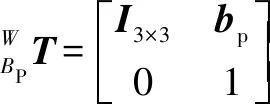
(10)

(11)

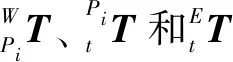
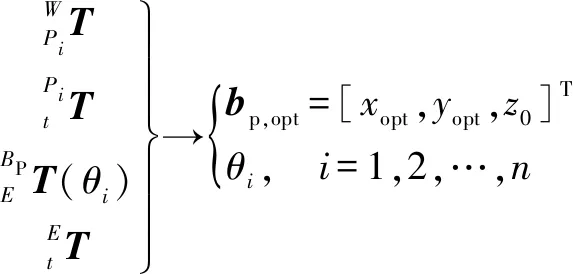
(12)

3 優化模型與方法

最優BP算法應滿足兩個要求：(1)機器人在每個關鍵加工點的剛度應盡可能高，以提高加工質量；(2)機器人應始終具有良好的運動性能，以保證其刀具能沿給定的加工路徑平穩、準確地運動。

3.1 優化模型

優化模型的建立包括兩個方面:(1)確定目標函數;(2)明確約束條件。考慮到基座BP優化的目的是盡可能提高機器人的剛度，將目標函數定義為最大全局剛度，即MSPI的最大化。因此目標函數的表達式為

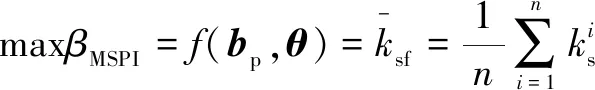
(13)

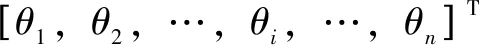
(1)關節距離

由于機械結構的限制，機器人各關節角,通常有明確的上、下限，即max和min(=1,2,…,6)。因此，關節距離約束的函數形式可以定義為

()=(,-min)(,-max)≤0

(14)

其中:=[,1,,2,,3,,4,,5,,6]，=1,2,…,。

(2)關節速度

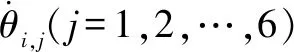
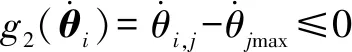
(15)

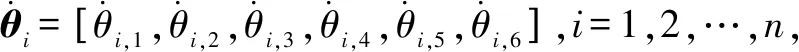
(3)奇異回避

當機器人處于或接近奇異位形時，機器人的自由度將丟失，進而影響機器人的控制精度。因此，在加工任務中，機器人必須遠離奇異位形，約束的函數形式可以定義為

()=()-≥0=1,2,…,

(16)

(4)避碰

在加工過程中，必須避免機器人與周圍環境之間的碰撞。為簡化避碰模型，本文作者采用工件和機器人的簡化模型，如圖3所示，工件與機器人之間的碰撞檢測將變得更加簡單。如果工件簡化模型中的所有點都不在機器人簡化模型的任何規則幾何內，則認為機器人與工件之間不存在碰撞，否則，就會發生碰撞。假設工件簡化模型中有個點，為其中之一。同時，在機器人的簡化模型中有個規則幾何對象，是其中之一，的質心為。考慮到的位置坐標是機器人關節角的函數，則碰撞檢測約束的函數形式可以定義為

()=(,)≥0=1,2,…,；=1,2,…,

(17)

式中:(·)為點到正則幾何曲面的最小距離。

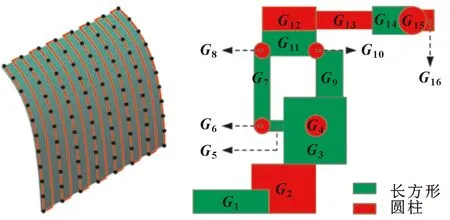
圖3 工件和機器人的簡化模型

如圖4所示，當規則幾何為球面、圓柱體和長方體時，(·)可分別定義為公式(18)—(20)，結果如下：

(,)=dist(,)-·

(18)

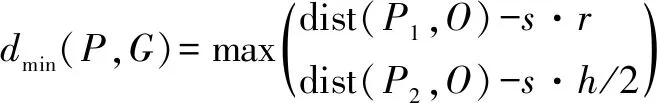
(19)

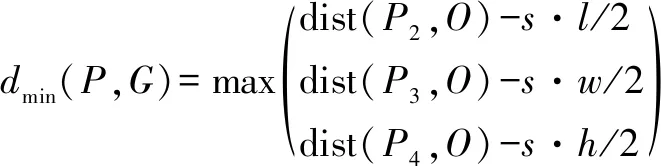
(20)

式中:、、、為正則幾何的尺寸參數；為大于1的安全系數，推薦值為1～1.5;距離dist(·)是兩點之間距離的函數。此外，如果點到規則幾何曲面的最小距離(記為)為正，則點不在幾何曲面內部，否則點在幾何內部。

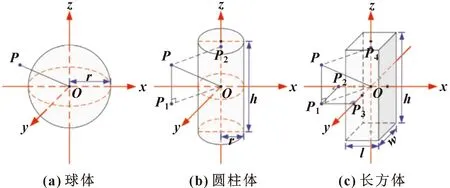
圖4 碰撞檢測原理

此外，為了保證優化方法的效率，基座BP的搜索范圍將受到限制。設BP上下限為=[,,],=[,,],優化模型可定義為

max(,)

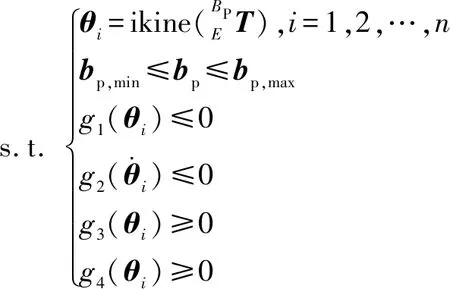
(21)

在式(21)所示的優化模型中，涉及到變量和，并且存在多個非線性約束，為了使優化模型更容易求解，有必要對其進行合理簡化。

由式(21)可知，機器人關節角度實際上是的函數。與此同時，約束條件(·)到(·)也是關節角的函數。因此，可以通過設計集成的IK算法來實現優化模型的簡化。集成的IK算法如算法1所示，其中IKflag為BP是否有效的標志，ikopt(·)為多個逆解的首選函數，且有效的BP值必須滿足(·)到(·)的約束條件。

算法1：

01:θ=zeros(n,6),IKflag=1

02:for i=1∶n

05:if g(θ)>0

06:IKflag=0,break

07:end

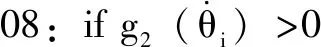
09:IKflag=0,break

10: end

11: if g(θ)<0

12:IKflag=0,break

13: end

14:if g(θ)<0

15:IKflag=0,break

16: end

17:end

18:return θ and IK

所有有效的BP集合稱為BP的可行域(簡稱RBP)，根據算法1，目標函數可以重新定義為

max=IKflag·(,)

(22)

最終優化模型為

max()

s.t.≤≤

(23)

3.2 優化方法

方程(23)是標準的有界非線性優化模型，可以采用內點法、序列二次規劃(SQP)法等多種方法求解，這些優化算法通常需要一個合適的初始值。在求解過程中，首先通過稀疏均勻網格分解法確定合適的初值，然后選擇SQP法計算最優值。具體的求解方法如下：

步驟1，確定初始基座BP的

由于約束條件(·)到(·)的存在，在笛卡爾子空間中，RBP的分布具有不規則和不連續的特征，因此有效的初始值應該滿足的條件是：(1)在RBP內部；(2)在最優BP所在的連通域；(3)靠近最優BP。考慮到這些要求，采用稀疏網格均勻分解方法將是一種較好的方法，不僅可以確定合適的初值，而且可以縮小最優BP的搜索范圍。該方法的原理圖如圖5所示。

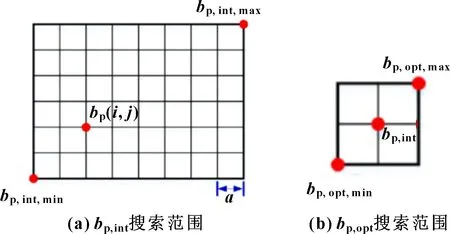
圖5 稀疏均勻網格分解

算法2：

01:b=fix(b/a)·a

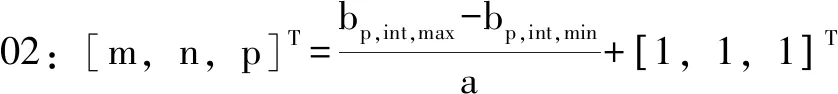
03:β=0

04:for i=1∶m

05: for j=1∶n

06: for p=1∶k

07:b=b+a·[i-1,j-1,p-1]

08:β(i,j,k)=F(b)

09: if β(i,j,k)>β

10: β=β(i,j,k)

11: maxind=[i,j,k]

12: end

13: end

14: end

15:end

16:b=b+a·(maxind-[1,1,1])

17:return band β

進一步，由圖5可知，最優BP搜索范圍()可以確定為：=[,]，其最小值和最大值表示式分別為=-[;;0],=+[;;0],其中是網格的邊長或分辨率。同時，為了保證的有效性和算法2的計算效率，在實際應用中將設為0.1 m或0.2 m。

步驟2,確定最優BP的

SQP是非常適合求解非線性約束優化模型的經典優化方法，已集成到各種通用優化算法工具箱或軟件包中，如MATLAB優化工具箱、IPOPT等。因此，在確定之后，使用SQP方法來求解是一個很好的選擇。在這里，利用MATLAB優化工具箱中的fmincon(·)函數求解最優BP，其調用格式為

=fmincon(-(),,,,,,,,option)

option=optimoptions(@fmincon,′Algorithm′,′sqp′)

根據MATLAB的SQP方法，可以精確求解。

4 模擬和實驗

為了說明基座BP優化方法的有效性，將分別通過仿真和實驗進行驗證。仿真結果主要說明了基座BP優化方法的有效性，即該優化方法能夠找到滿足～約束且MSPI最大的基座位置，實驗主要用于驗證性能指標MSPI與加工質量之間的對應關系。

4.1 模擬環境

以風機葉片表面拋光仿真為應用背景，如圖6所示，風機葉片的整體尺寸可以達到59.5 m×2.5 m×4.0 m，遠遠超出了機械手的操作范圍。因此，通常將風機葉片表面預先劃分為幾個待加工的子區域。綠色區域是其中的一個子區域，其大小為1.6 m×0.3 m×1.2 m，及其邊界尺寸參數=[-0.80,0.80,-0.34,0.07,1.44,2.66] m。機器人最大距離可達=1.90 m，底架高度為=0.75 m，則的搜索范圍可為=[-1,1.10;-2.20,-0.30;0.75,0.75] m。此外，機器人確定的約束條件如表2所示。

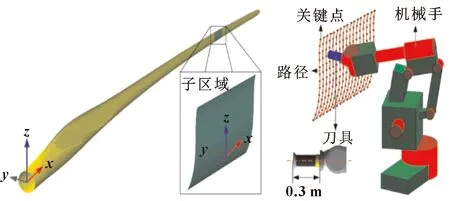
圖6 風機葉片表面磨削仿真環境

表2 g1(·)到g4(·)的約束

4.2 仿真結果

如圖7所示，給出了算法2得到的MSPI等高線圖，同時圖中也標出了準RBP的邊緣和最優BP精確搜索范圍的邊緣。另外，圖中白色部分表示該區域沒有有效的BP，但準RBP中的白色部分可能仍有有效的BP，這主要是由于網格分辨率較低所致。

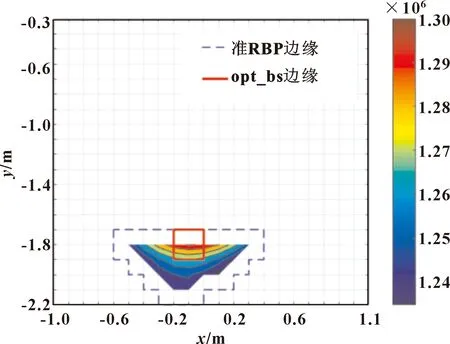
圖7 平均剛度性能指標(MSPI)等值線圖

根據等高線地圖，可以確定初始BP為=[-0.10;-1.80;0.75] m,精確搜索范圍=[-0.2,0.00;-1.90,-1.70;0.75,0.75] m。然后最優的BP可以通過SQP方法得到，其值為=[-0.099 4;-1.728 8;0.750 0] m。

為了進一步證明優化方法的有效性，分別給出了最優BP處各關鍵點的關節角度、關節速度、和的分布圖，如圖8—圖11所示。

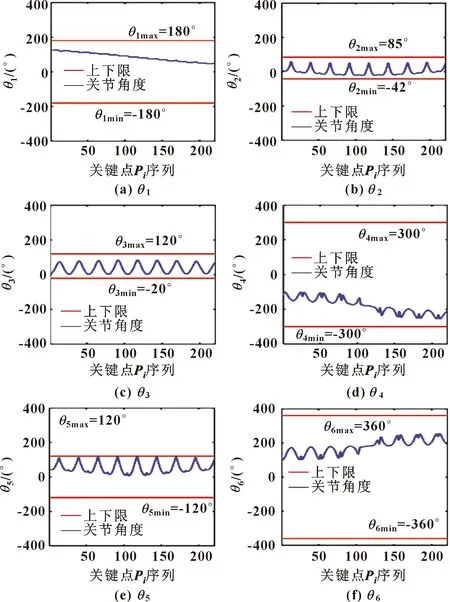
圖8 加工路徑上各關鍵點Pi的關節角度

圖8中，藍線表示加工路徑上各關鍵點的關節角度，紅線表示關節角度的上下限。圖9中，藍線表示加工路徑上各關鍵點的關節角速度，紅線表示關節角速度的正負最大值。在圖10中，藍線表示機器人在加工路徑上各關鍵點處的KCI值，紅線表示KCI的最小值。在圖11中，曲線分別表示了機器人簡化模型中加工對象的簡化模型與規則幾何(=1，2，…，15)之間的最小距離，的分布如圖3所示。從這些圖形中可以看出:機器人的關節角度和關節角速度均在限定范圍內，機器人的KCI值均大于最小值，所有關鍵點上(=1，2…，15)的值均大于0。

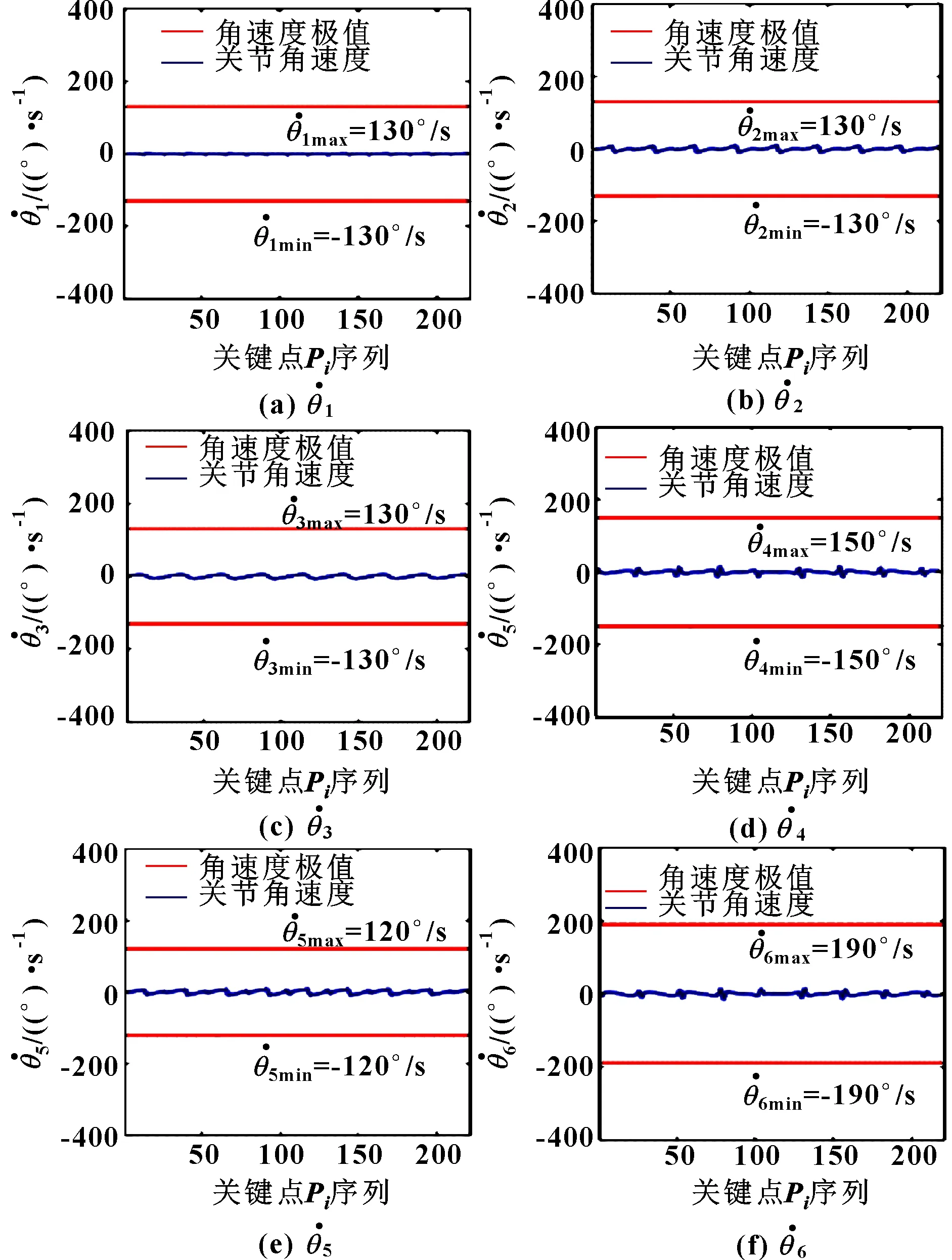
圖9 加工路徑上各關鍵點Pi的關節角速度

因此，在最優BP算法中，結果滿足(·)～(·)約束條件，保證了機器人的運動性能。上述分析表明了所提出的基座BP優化方法的正確性，該方法能有效地找到全局剛度性能最大的基座位置，滿足實際應用中需要考慮的所有運動約束條件，這對于提高移動機械手的操作性能具有重要意義。

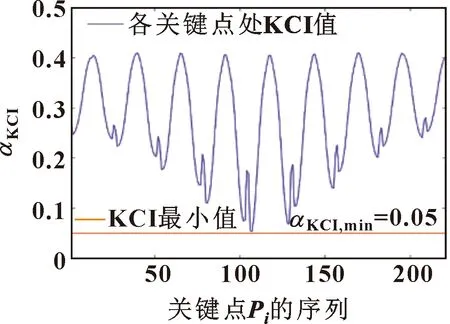
圖10 每個關鍵點Pi的KCI

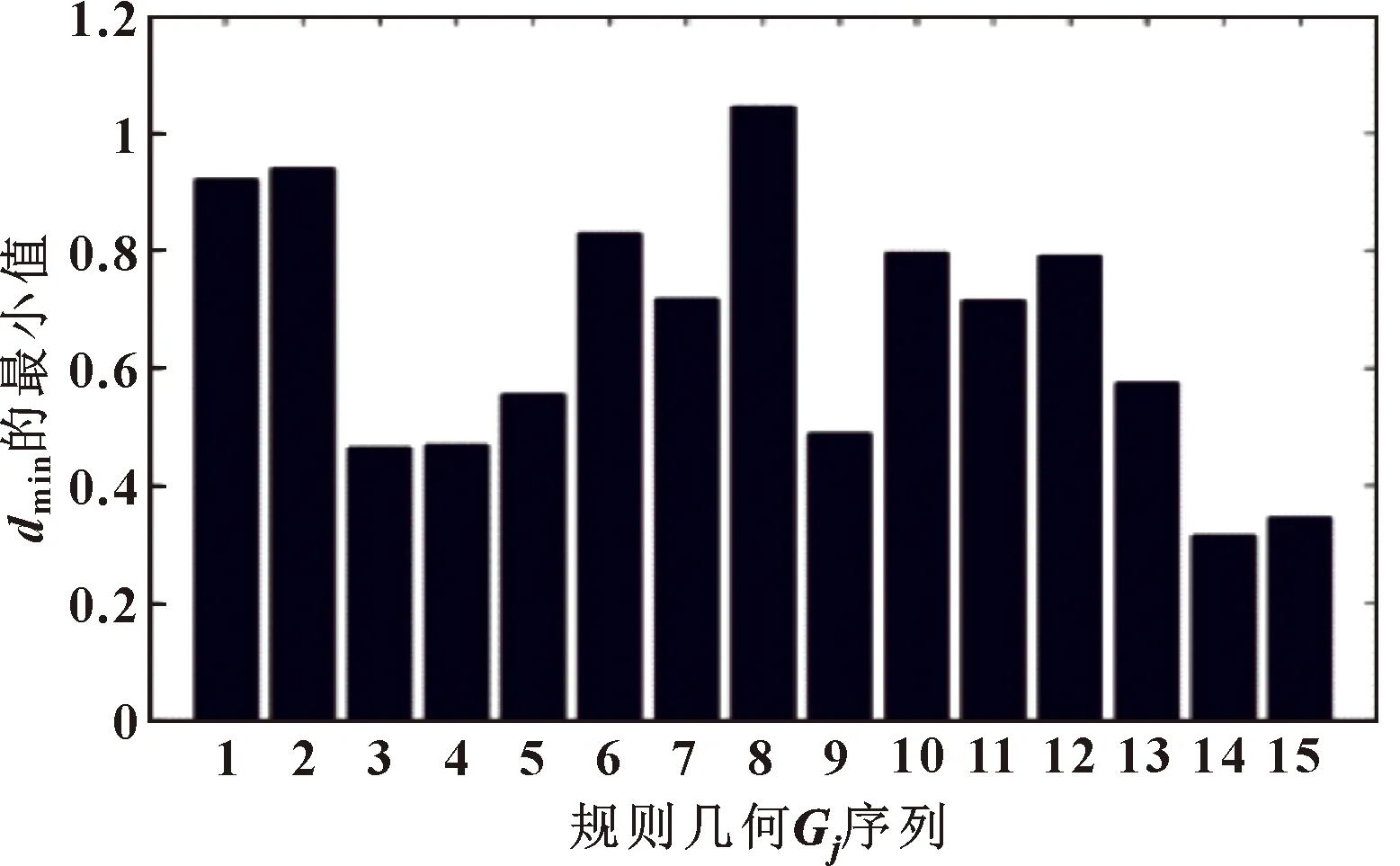
圖11 Gj所有關鍵點的dmin

5 結論

針對六自由度機械手在大型復雜零件的加工能力，提出一種面向移動機械手加工基座位置優化方法，其目標是在保證機器人運動性能的同時，優化機器人的剛度性能。建立了機械手運動性能指標和全局剛度指標，在此基礎上綜合考慮了機械手關節距離、關節速度、奇異回避和避碰等多約束條件，通過采用稀疏均勻網格分解和序列二次規劃(SQP)方法對機械手最優基座位置進行求解。最后通過仿真分析和實驗結果驗證了該優化方法的有效性。