一類帶組合非線性項波動方程解的破裂

張文君，韓偉，明森，杜嘉儀

（中北大學理學院，山西 太原 030051）

0 引言及主要結論

隨著現代科學技術的飛速發展，偏微分方程作為一門重要的學科被廣泛應用于諸多領域。波動方程是偏微分方程的重要分支，常被用于研究波的傳播及弦的微小振動等物理現象。波動方程是一類典型的雙曲型方程，具有重要的物理背景、理論意義和應用價值。波動方程已成為非線性發展方程研究的熱點問題之一，非線性波動方程的穩定性理論、散射理論及其破裂性態的研究可以更好地揭示波的傳播規律等。由于非線性項的影響，波在傳播過程中會變得陡峭直到破裂。由于現實中存在摩擦現象，因而阻尼等因素會影響物理系統的能量，結合非線性外力作用會影響解的破裂性態與生命跨度估計。然而，由于阻尼項系數依賴于時間變量，從而會對物理系統的能量以及振幅產生更為復雜的影響。因此，本文研究帶阻尼項波動方程解的破裂性態，更深刻和全面地認識波傳播理論中的物理現象，為數值模擬和實際應用提供理論支撐，具有重要的意義。

近來，許多數學工作者對波動方程的解的破裂及其生命跨度的上界估計與非線性項指數和空間維數的關系進行了大量的研究［1-20］。Strauss W A［1］得到波動方程utt-Δu=|u|p的初值問題具有Strauss臨界指數pc(n)。當n≥2時，pc(n)是二次方程

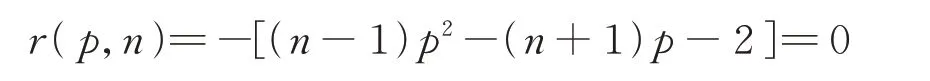
的正根；當1＜p≤pc(n)時，問題的解會在有限時間內破裂；當p＞pc(n)時，問題存在整體解。文獻［2］研究了變系數波動方程的初邊值問題，其中非線性項為|u|p。文獻［4］研究了帶導數非線性項的波動方程ut-Δu=a2|ut|p+b2|?u|p(a2+b2＞0)具有Glassey臨界指數pG(n)=1+2(n-1)。文獻［5］在n維全空間中研究了次臨界指數帶散射阻尼項μ(1+t)-βut(β＞1)的波動方程，其中非線性項為|u|p。文獻［6］研究了帶散射阻尼項與尺度不變阻尼項的波動方程，其中非線性項為|ut|p。文獻［7］在次臨界指數時研究了帶散射阻尼項與組合非線性項的波動方程。利用檢驗函數方法和迭代方法得到解的生命跨度的上界估計。文獻［12］研究了帶散射阻尼項和負質量項的波動方程，得到解的生命跨度的上界估計。文獻［18］在Rn中研究了半線性波動方程耦合系統解的破裂。

本文在外區域上研究如下變系數波動方程的初邊值問題

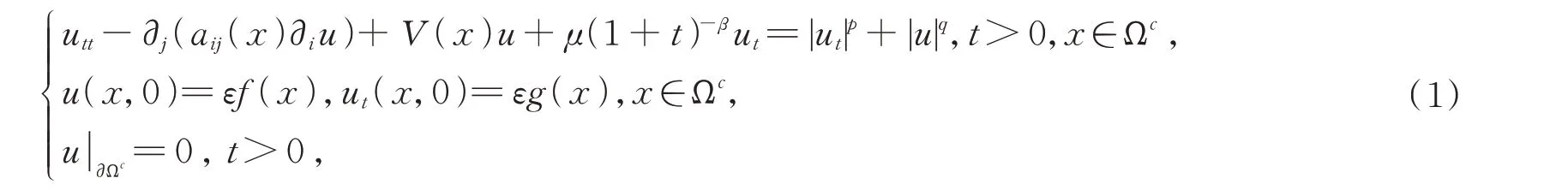
其 中μ＞0，β＞1，Ωc=RnB1(0)。supp(f，g)?BR(0)∩Ωc，其 中BR(0)={x||x|≤R}，R＞2。f(x)，g(x)≥0且f(x)，g(x)不恒等于0。A(x)={aij(x)}n i，j=1表示光滑實對稱n×n矩陣，并且存在正常數C使得C-1|ξ|2≤aij(x)ξi ξj≤C|ξ|2，?ξ∈Rn，x∈Ωc。此處采用愛因斯坦記號，重復指標i，j表示求和。當|x|＞R＞2時，aij(x)=δij，其中δij為Kroneckerδ函數。V(x)表示位勢。

本文擬結合文獻［7，12］，在外區域上研究變系數問題（1）。主要結果如下。

定理1設n≥1，V(x)＞0，且V(x)≤C(1+|x|2+δ)-1，C＞0，δ＞0均為常數。aij(x)=δij。假設問題（1）的解滿足suppu?{(x，t)∈Ωc×[0，T)||x|≤t+R}。若p＞1且

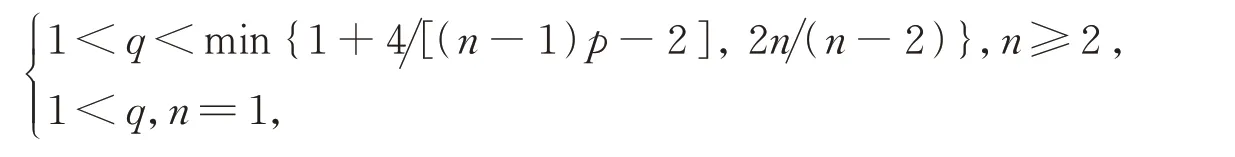
則解u會在有限時間內破裂，且生命跨度T(ε)的上界估計為T(ε)≤Cε-2p()q-1[2q+2-(n-1)p(q-1)]，其 中C是與ε無關的正常數。

定理2設n≥2，V(x)＞0，且V(x)≤C(1+|x|2+δ)-1，C＞0，δ＞0均為常數。aij(x)=δij。設問題（1）的解滿足與定理1相同的條件。當p＞2n(n-1)，1＜q＜(n+1)(n-1)時，解u會在有限時間內破裂，且生命跨度T(ε)的上界估計為

定理3設n≥1，V(x)＞0，且V(x)≤C(1+|x|2+δ)-1，C＞0，δ＞0均為常數。aij(x)=δij。假設問題（1）的解滿足與定理1相同的條件。則解的生命跨度上界估計為

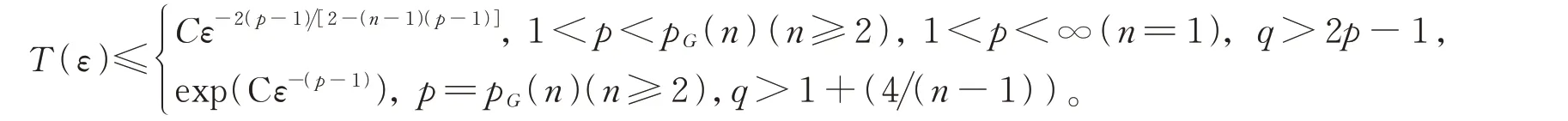
定理4設n=1時p＞1，n≥2時1＜p＜pG(n)，V(x)≤-K0，其中K0＞0。若問題（1）的解滿足與定理1相同的條件，則解u會在有限時間內破裂，且生命跨度的上界估計為T(ε)≤Cε-2p(p-1)r(p，n)。

注1當V(x)=0時，問題（1）為帶散射阻尼項的變系數波動方程的初邊值問題。類似于文獻［7］的證明過程，可知定理1-3的結論仍成立。

注2文獻［5-6］在全空間中研究波動方程的初值問題，其中非線性項分別為|u|p，|ut|p。本文在外區域上研究帶組合非線性項的變系數問題（1）。通過構造乘子，利用檢驗函數方法與迭代方法，得到問題（1）解的生命跨度的上界估計。當V(x)＞0時將文獻［7］中研究的問題推廣至外區域上帶位勢項的變系數問題。當V(x)=0時將文獻［7］研究的問題推廣至外區域上變系數問題。當V(x)≤-K0時將文獻［12］中研究的問題推廣至外區域上帶負位勢項的變系數問題。

1 一些引理

引理1［3］當V(x)≥0時，存在檢驗函數φ0(x)，φ1(x)∈C2(Ωc)滿足

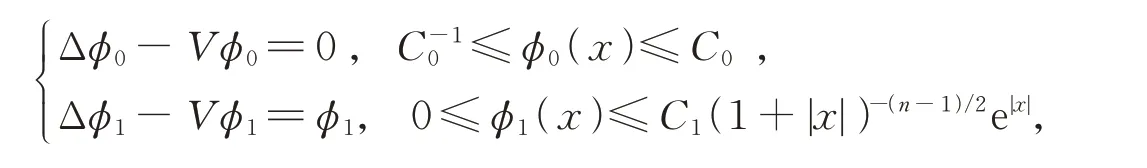
其中C0，C1為正常數。特別地，當V(x)=0時，有

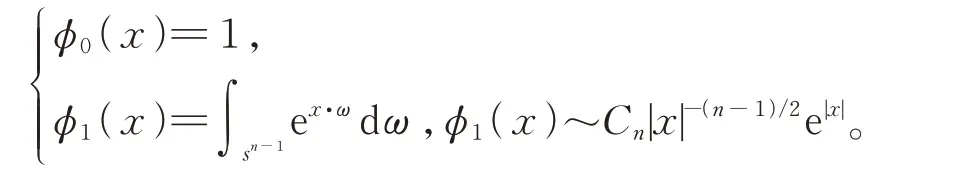
現記ψ(x，t)=e-tφ1(x)，其中φ1(x)如引理1中所述。

引理2［2］設p＞1，φ0(x)與φ1(x)滿足引理1中的條件。則?t≥0，有

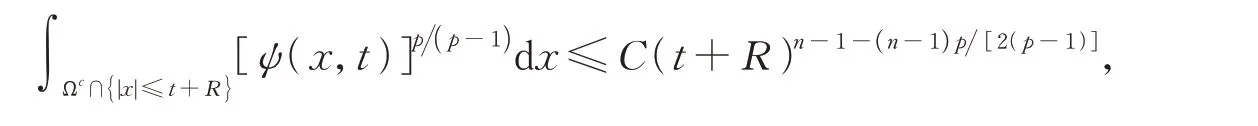
其中C為正常數。

令m(t)=exp(μ(1+t)1-β(1-β)，則有m(0)≤m(t)≤1。

引理3［7］設ψ(x，t)滿足引理，u是問題（1）在[0，T)上的弱解。記

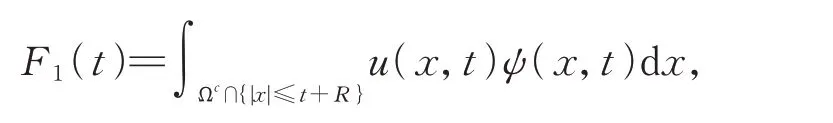
則對?t≥0，有

引理4［2］設φ0(x)，φ1(x)滿足引理1中的條件，并且

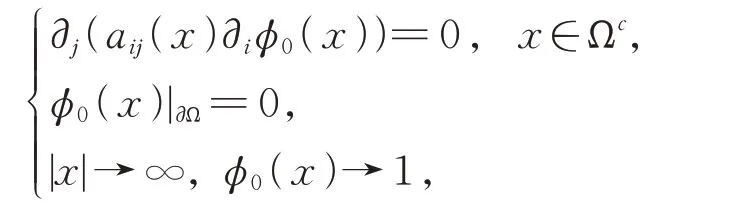
其中φ0(x)滿足x∈Ωc，0＜φ0(x)＜1。

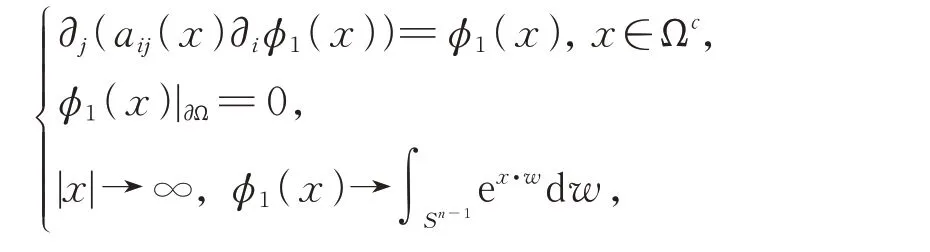
并且存在常數C1＞0，使得0＜φ1(x)≤C1(1+|x|)-(n-1)2e|x|，?x∈Ωc。

引理5［7］設ψ(x，t)滿足引理1所述，u是問題（1）在[0，T)上的弱解。記

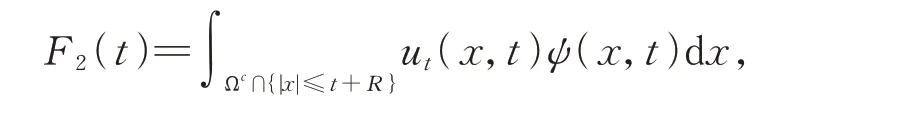
則對?t≥0，有

首先，給出問題（1）的弱解的定義。

定義1當V(x)＞0，aij=δij時，問題（1）的弱解滿足

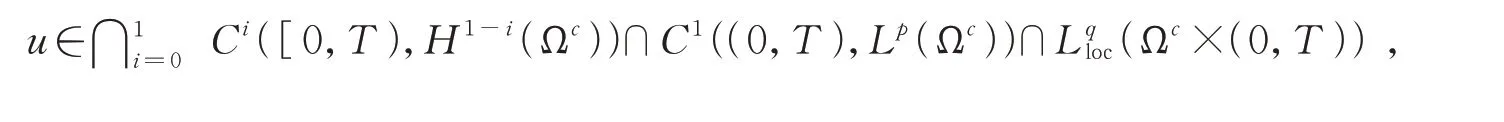
并且

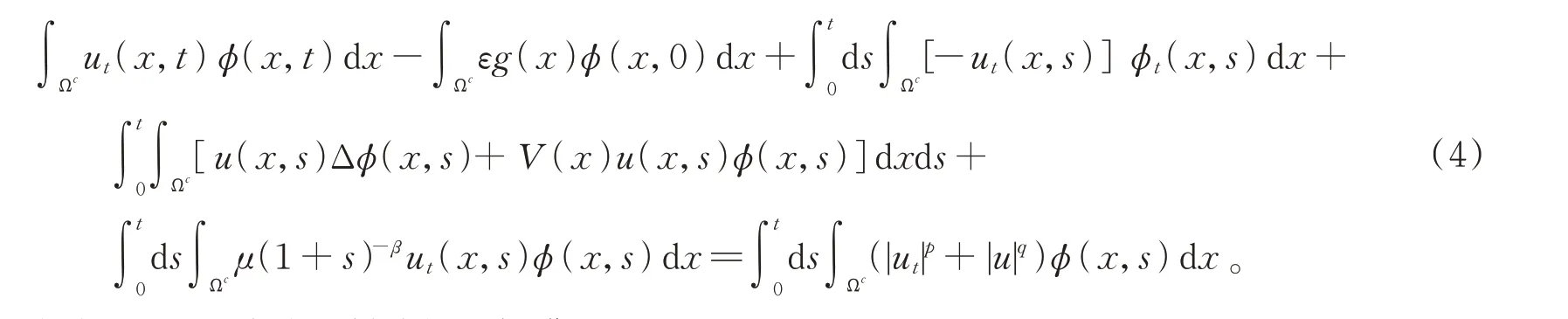
定義2當V(x)≤-K0時，問題（1）的弱解滿足

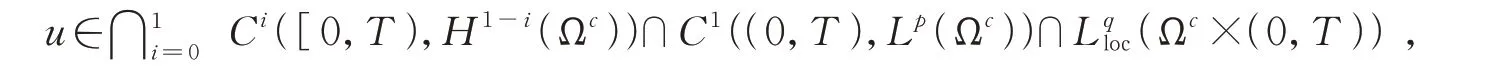
并且

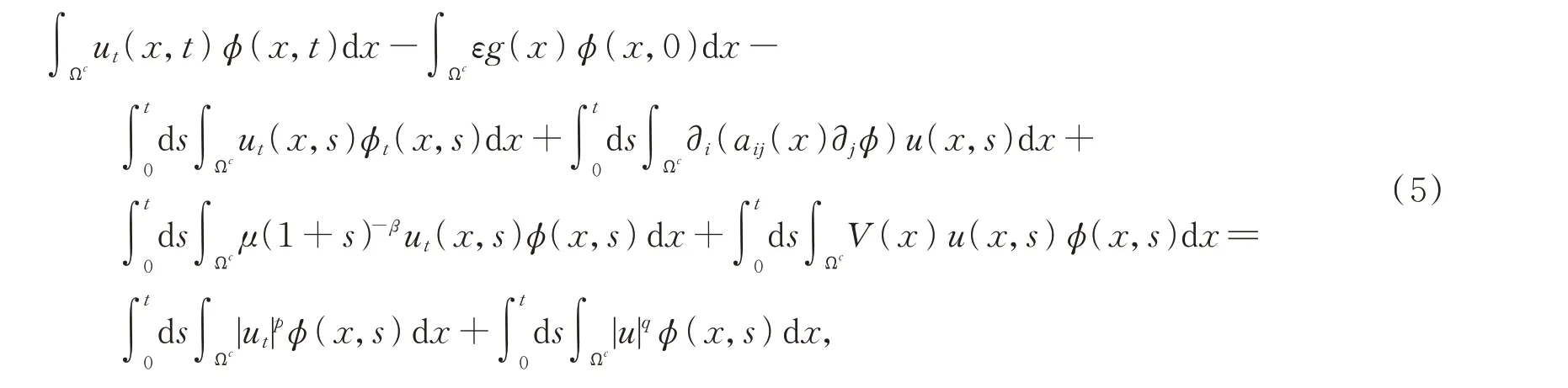
其中φ∈C∞0(Ωc×[0，T))，t∈[0，T)。

2 定理1的證明

引入如下函數

其中u是問題（1）在[0，T)上的解，φ1(x)如引理1所述，ψ(x，t)=φ1(x)e-t。

當V(x)＞0時，利用aij(x)=δij，在式（1）兩邊同乘以φ0(x)，并積分計算可知

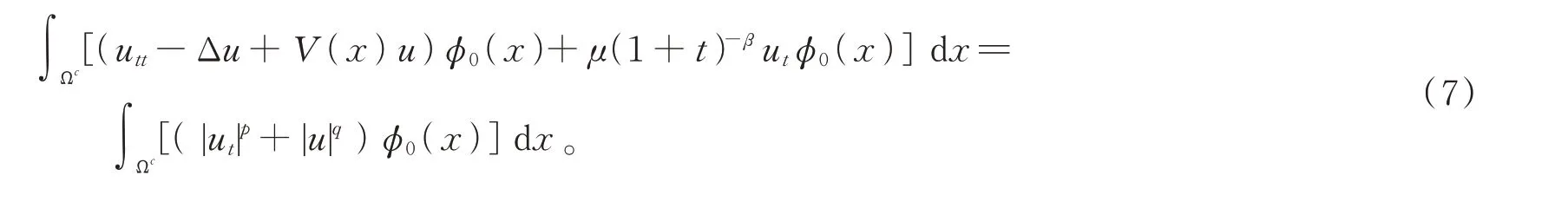
由引理1可得

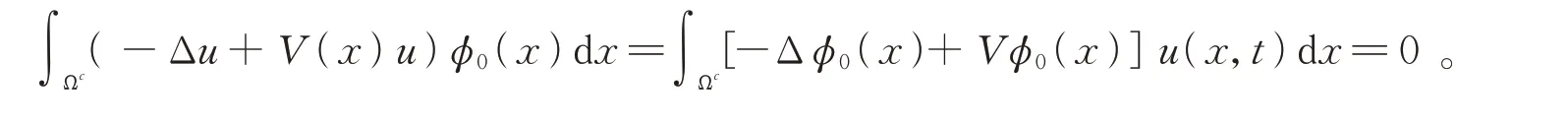
從而

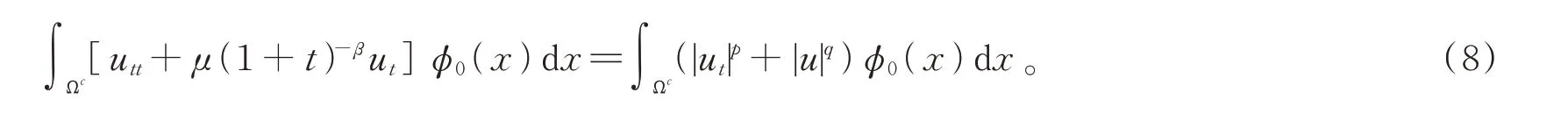
下面建立F0(t)的估計。

在式（4）中令φ(x，s)=φ0(x)，其中|x|≤s+R，結合引理1和式（8），得到

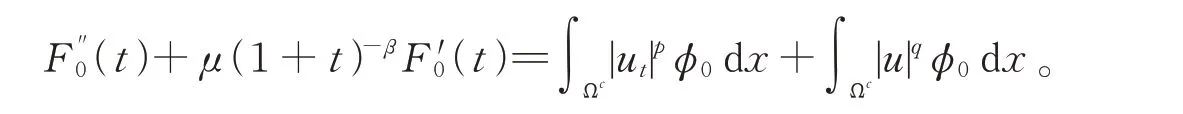
兩邊同乘以m(t)，利用F0(0)＞0，F′0(0)≥0，m(0)≤m(t)≤1，則?t≥0，計算可得

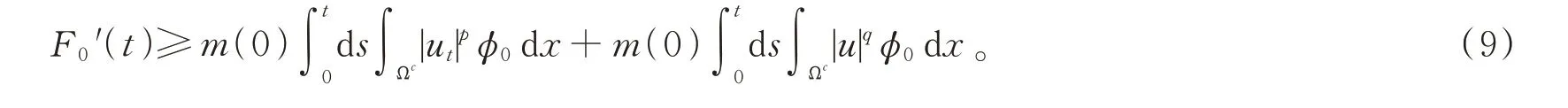
類似于文獻［7］中的計算，可知F1(t)的估計滿足引理3中的式（2）。

下面建立F2(t)的估計。

由引理2，引理5以及H?lder不等式得

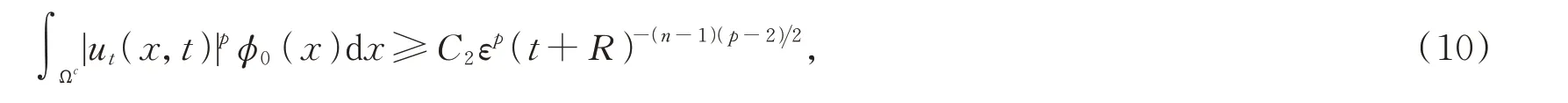
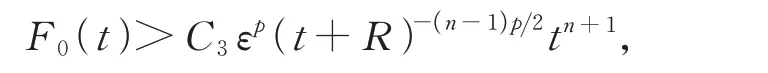
其中C3=m(0)C2[n(n+1)]。利用H?lder不等式可知

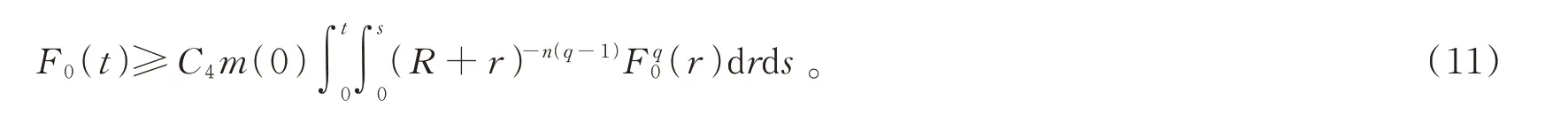
下面利用迭代方法建立問題（1）解的生命跨度T(ε)的上界估計。假設F0(t)滿足

且D1=C3εp，a1=(n-1)p2，b1=n+1。將式（12）代入式（11）得到

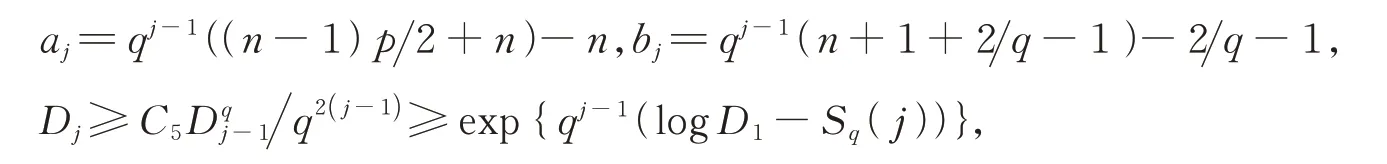
當t≥1時，J(t)≥log(D1t1+2(q-1)-(n-1)p2)-C6，C6=((n-1)p2+n)log 2+Sq(∞)。所以若t≥，則有J(t)≥1。在式（14）中令j→∞，可知F0(t)→∞，從而得到定理1中生命跨度的上界估計。定理1證畢。

3 定理2-3的證明

定理2的證明根據式（9）可得

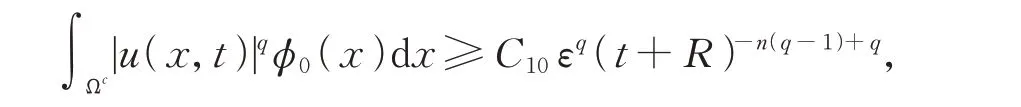
利用1＜q＜(n+1)(n-1)，可得定理2中生命跨度的上界估計。定理2證畢。

定理3的證明結合文獻［6］和定理1的證明，令

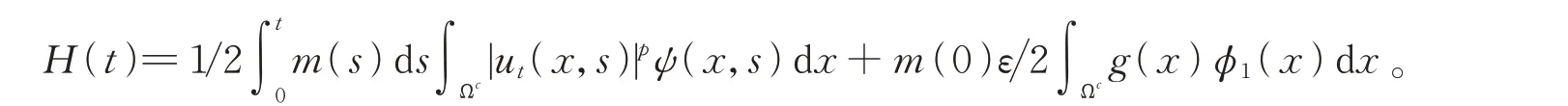
根據m(0)≤m(t)≤1可知，m1-p(t)≥1。利用引理2，結合G(t)＞0，得到

其中H(0)=(m(0)C0，g2)ε＞0。通過求解常微分不等式（17），即得定理3中的生命跨度估計。定理3證畢。

4 定理4的證明

首先建立F0(t)的估計。當V(x)≤-K0時，在式（5）中令φ(x，s)=φ0(x)，由引理4得到

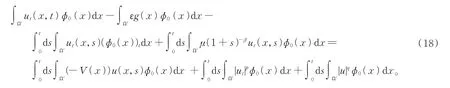
利用V(x)≤-K0，在式（18）兩邊關于t求導，計算得到

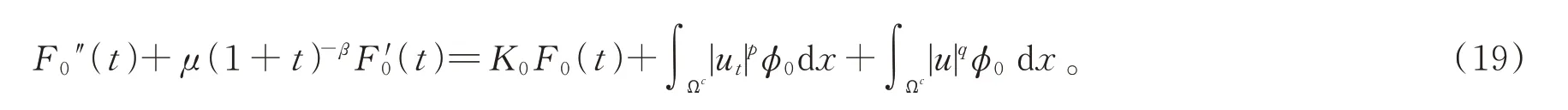
在式（19）兩邊同乘以m(t)，并在[0，t]上積分可得

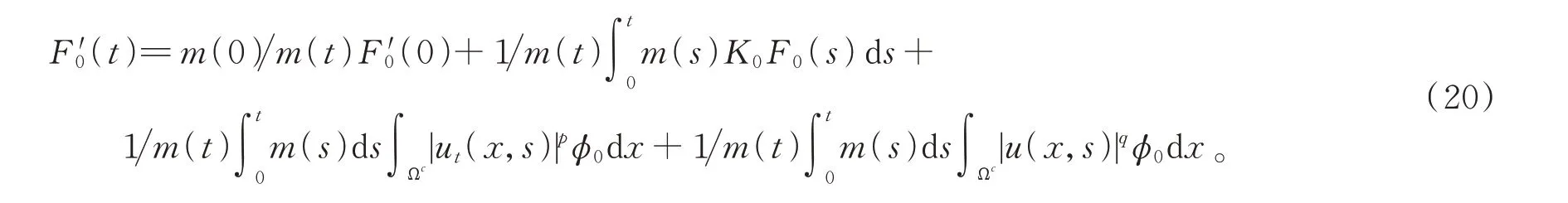
類似于文獻［12］中的分析，可得F0(t)＞0，進而得到F′0(t)≥0。

下面建立F1(t)的估計。對式（5）求導并且兩邊同乘以m(t)并在[0，t]上積分，可知

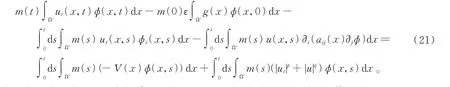
在式（21）中令φ(x，t)=ψ(x，t)=e-tφ1(t)，則φt=-φ，φtt=?i(aij(x)?jφ(x，s))。于是

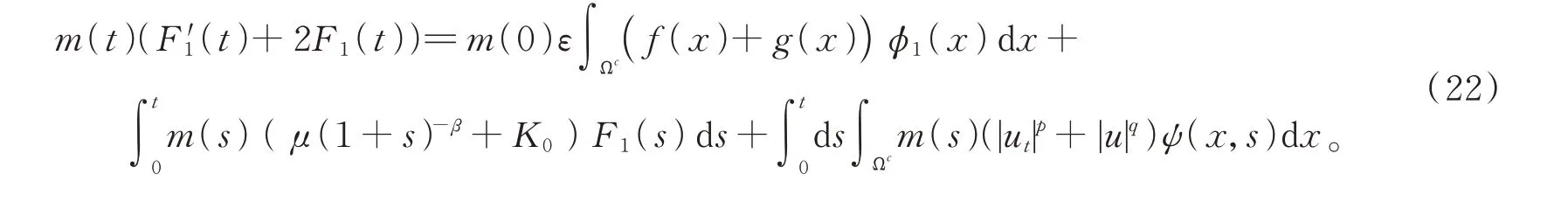
計算得到

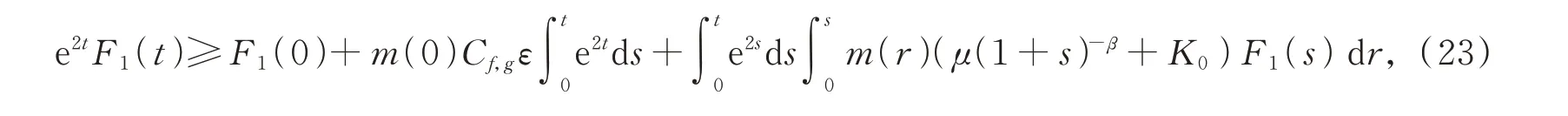
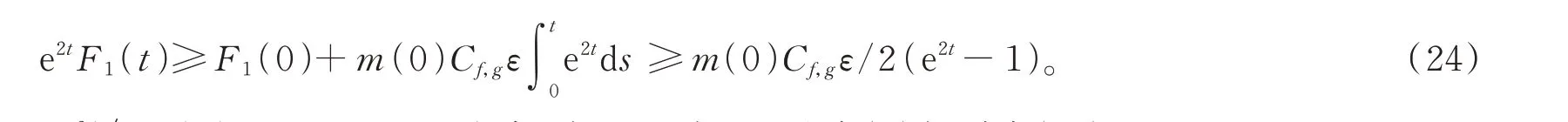
從而F1(t)＞(1-e-2)2m(0)Cf，0ε，t≥1。根據引理2，引理5及式（9）得到式（11）。

類似于利用迭代方法證明定理1的過程，即可得到定理4中解的生命跨度估計，此處略之。定理4證畢。