遺傳算法與LuGre摩擦模型的非線性摩擦力觀測器設計

黃智鵬，徐悅鵬，曹瑞康，付承偉，任 旺，孔祥東，李文鋒

(燕山大學 機械工程學院，河北 秦皇島 066004)

引言

摩擦現象廣泛存在于機械系統中，特別是對控制品質要求較高的伺服控制系統，摩擦的出現會降低其跟蹤精度，產生控制極限環以及不必要的爬行現象。特別當系統處于低速運動時，摩擦現象會表現出復雜的強非線性特性，無法找到準確描述這些現象的非線性函數[1]；而且摩擦非線性是摩擦因素中最影響伺服進給系統精度的摩擦現象[2]，對系統的低速伺服性能影響尤為顯著[3-5]。

為此，諸多學者對于非線性系統的控制技術進行了廣泛的研究。李淵等[6]對電液伺服泵控系統中的非線性理論進行了研究，提出了廣義排量的壓力控制策略，通過試驗和仿真驗證了對系統控制的效果。趙爽等[7]針對閥控液壓馬達系統受到的非線性擾動問題，提出了一種三階線性控制器，采用跟蹤誤差前饋與擴張狀態觀測器相分離的辦法，增強了液壓伺服系統的抗干擾能力。范珂等[8]針對不確定性及外部干擾下主動升沉補償系統的非線性控制問題，提出一種基于擴展干擾觀測器自適應魯棒控制器，通過李雅普諾夫函數證明整個閉環系統的穩定性。馮浩等[9]針對挖掘機器人伺服系統存在高度非線性、參數不確定和未建模動態等諸多不利因素，提出了一種結合徑向基函數神經網絡的非線性滑模控制器，提高了系統的控制精度和魯班性。謝宜含等[10]針對機電伺服系統存在較多不確定性的現象，設計了一種自適應非線性控制策略，不僅有效補償了系統不確定性，而且實現了非線性控制器與線性頻寬參數的一體化設計。何耀濱等[11]針對大行程直線運動平臺復雜的非線性時變系統的不確定因素，將系統的速度、位移作為狀態變量，設計一個線性自抗擾控制器，通過與PID控制算法進行比較，提升了運動平臺的響應速度和精度。

采用基于摩擦模型的摩擦補償控制可以有效地對摩擦進行一定程度上的預測，提高控制精度。因此，本研究在系統控制策略設計中，將摩擦現象進行模型化分析并納入系統特性，并通過遺傳算法完成系統摩擦參數的辨識，提高系統控制精度。

1 摩擦現象數學模型

摩擦現象的數學模型可根據是否由微分方程描述大致分為兩類：靜態摩擦模型和動態摩擦模型。常見靜態摩擦模型有庫倫摩擦模型、黏性摩擦模型、Stribeck摩擦模型、Karnopp模型、Armstrong模型。常見的動態模型有Dahl摩擦模型、鬃毛摩擦模型、LuGre摩擦模型[12]。采用基于摩擦模型的摩擦補償控制可以有效地對摩擦進行一定程度上的預測，提高控制精度。

1.1 靜態摩擦模型

一般的線性系統數學模型所采用的摩擦模型為靜態摩擦模型，多為庫倫摩擦、靜摩擦、黏滯摩擦和Stribeck摩擦等幾種特性的組合。通過摩擦力與物體相對運動速度的關系揭示的各個摩擦特性的主要特點如圖1所示。

圖1 經典摩擦特性示意圖

經典常見的摩擦模型由庫倫摩擦特性、黏性摩擦特性和靜摩擦特性三者共同描述。庫倫摩擦揭示了當物體間相對運動速度不為0時，相對運動方向與摩擦力方向相反的現象；黏性摩擦體現了黏性力對物體運動的影響；靜摩擦則補充了當物體間相對運動速度為0時摩擦力的變化特性。

靜摩擦摩擦模型如下：

(1)

式中,Ft——外力，N

Fs——最大靜摩擦力，N

v——相對滑動速度，mm/s

庫侖摩擦模型結合黏性摩擦模型如下：

Ff=Fcsgn(v)+Bv

(2)

式中，Fc——庫倫摩擦力，N

B——黏性摩擦系數，N·s/m

上述模型對物體間最大靜摩擦力到滑動摩擦力過渡的數學描述是突變的，然而Stribeck摩擦現象表明，物體間相對運動速度在較低時摩擦力的變化是呈現負斜率特性的。Karnopp模型結合了對Stribeck摩擦現象的數學描述，并通過設定零速度區間對相對運動速度進行劃分，即當相對速度值位于該區時，速度被等效為0，視為靜摩擦。但是零速區間的選取存在一定困難，無法真實反映零速附近摩擦力的變化情況，公式如下所示：

(3)

F(v)=[Fs+(Fs-Fc)e-(v/vs)δ]sgn(v)+Bv

(4)

式中F(v)——對Stribeck摩擦現象以及黏性摩擦的數學描述

δ——經驗常數，取值通常為2

DV——所選擇的零速區間

靜態摩擦模型從宏觀方面體現了物體間相對運動速度穩定時摩擦力所表現的靜態特性，但是當速度發生變化，諸如預滑移、可變靜摩擦力、摩擦滯后等摩擦微觀非線性動態特性無法從中得以體現。因此，采用單一的靜態摩擦模型進行補償控制并不能取得較為理想的控制效果。

1.2 動態摩擦模型

通過一階微分方程對摩擦現象的動態微觀行為描述，逐漸形成了動態摩擦模型。其中被普遍應用的動態摩擦模型為Dahl摩擦模型、復位積分摩擦模型、鬃毛摩擦模型以及LuGre摩擦模型。相較于其他模型，LuGre模型，結合了Dahl模型的鬃毛摩擦思想，同時引入對摩擦預滑動位移特性的描述，能夠以較為精確的數學語言同時描述摩擦力的動態特性和靜態特性。圖2為LuGre摩擦模型的基本原理圖。

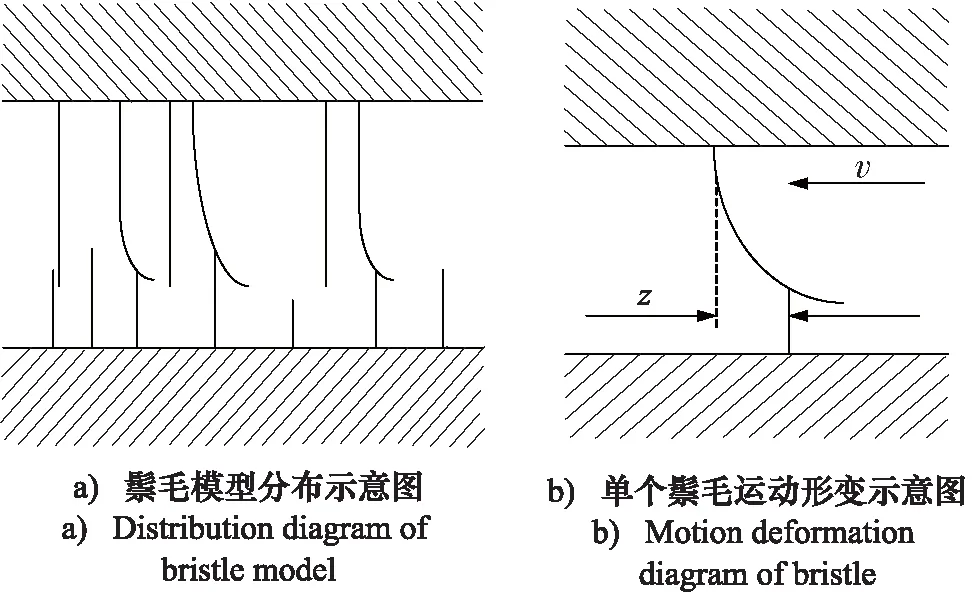
圖2 LuGre摩擦模型原理圖

如圖2所示，LuGre摩擦模型關注運動物體接觸面間的相對微觀運動。該模型假設物體之間通過無數具有彈性形變特性的鬃毛接觸，當有切向力施加于鬃毛時，鬃毛會像彈簧一樣產生形變并發生預滑移，從而由此產生靜摩擦力，此時鬃毛的彈性形變量約等于滑動位移。當切向力變得足夠大，其中一部分鬃毛發生過度偏移后便會彼此滑脫，物體間相對運動由此產生，同時形成滑動摩擦力，此時鬃毛的彈性形變量由物體間的相對運動速度決定。實際運動中，由于接觸面形狀不規則，鬃毛彼此間的接觸形態被認為是高度隨機的。因此LuGre模型研究的是鬃毛的平均運動行為，其表達公式如下：

(5)

g(v)=σ0[Fc+(Fs-Fc)e-(v/vs)2]

(6)

(7)

式中,Fc,Fs——靜摩擦力參數，N

z——鬃毛平均彈性形量，mm

g(v)——取決于物體材料、潤滑、溫度等因素的正函數

σ0——剛度系數，N/m

σ1——阻尼系數，N·s/m

σ2——黏性摩擦系數，N·s/m

vs——Stribeck速度，mm/s

下面對LuGre摩擦模型的穩定性和可行性進行證明。假設物體間的相對運動速度v是分段函數，連續且有界，函數g除零點外有界，由此可得：

≤L|z1-z2|

(8)

由于v是有界的，且g>ε>0，該利普希茨連續條件保證了摩擦模型解的存在性和唯一性。

假設00時，那么|z(t)|≤a。

取李雅普諾夫函數V(t)=z2/2，當z(t)≠0時，顯然V(t)>0是恒成立的，那么：

(9)

當|z|>g(v)時，由于函數g嚴格為正且有界，那么集合Ω={z:|z|≤a}是式(9)解的不變集，因此所有z(t)解的軌線始于Ω并保留于其中。從物理學角度而言，物理系統的耗散特性與能量有關。對于控制系統上的數學描述，亦可借用該原理描述反饋系統的穩定性。系統的數學模型可以被定義為能夠將輸入映射到輸出的算子，式(9)可被認為是輸入-輸出映射算子，由此可證明該映射關系是耗散的。

(10)

對兩邊同時取積分，可得:

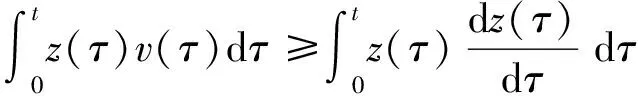
≥V[z(t)]-V[z(0)]

(11)

顯然，式(11)是自然耗散的。

由上述公式可以看出，LuGre摩擦模型清晰簡潔，與其他模型相比，該模型能夠平滑地從當前摩擦狀態過渡到另一摩擦狀態，在一定程度上具有良好的連續性。此外，該模型可以將庫倫摩擦、黏性摩擦、摩擦滯后、Stribeck效應和摩擦記憶等復雜的非線性摩擦特性較為準確地表達出來。而其中的未知參數可采用參數辨識方法獲得，為多種摩擦補償算法的設計與應用提供了可能性。

2 基于遺傳算法的Lugre摩擦模型參數辨識

2.1 模型參數辨識機理

遺傳算法是一種基于自然界中生物間“物競天擇，適者生存”的演化法則的算法。相較于傳統算法，其求解方案起始于群體數據，并非單個點。其良好的全局搜索能力可以快速地得到解空間的全體解并同時避免陷入局部最優解的快速下降陷阱。此外，該算法的內在并行特質提供了具有更快求解速度的分布式計算。就其本質而言，遺傳算法是一種高效、并行、全局搜索的方法。

圖3展示了遺傳算法基本流程圖。首先，遺傳算法在進行搜索前會將解空間的數據進行編碼，形成基因串型結構數據，并同時隨機生成n個初始串數據結構，作為初始種群；然后，根據需要求解或優化目標函數，計算群體中每個個體的目標函數值，并通過給定的適應度函數對相關個體作出評價；隨后，按照個體的適應度和一定的選擇函數對父代種群進行擇優選擇，同時基于預設概率對選定的個體進行交叉、變異等操作，從而產生子代種群；接下來，算法會對子代種群重復執行上述操作，直至輸出滿足終止條件的最優結果。

圖3 遺傳算法辨識流程圖

通過遺傳算法分別對LuGre模型中的靜態摩擦參數和動態摩擦參數[19]進行辨識，從而為摩擦補償提供較為準確的模型以獲取更優的控制效果。

2.2 靜態摩擦參數辨識

F=σ0z+σ2v

=[Fc+(Fs-Fc)e-(v/vs)2]sgn(v)+σ2v

(12)

根據上述公式可知，待辨識參數向量設定如下:

(13)

那么參數辨識誤差為:

e(x,vi)=ui-F(x,vi)

(14)

其中：

(15)

取誤差函數的平方和作為目標函數:

(16)

取適應度函數為:

(17)

遺傳算法中需要設定的相關參數將在后面的仿真小節中給出，結合上述推導出的供述，便可獲得LuGre摩擦模型的靜態摩擦參數。

2.3 動態摩擦參數辨識

將2.2節中靜態摩擦參數辨識得到的最優結果將作為動態摩擦參數辨識的基礎。利用系統輸出的加速度以及系統輸出的控制力即可進行動態摩擦參數辨識。待辨識參數向量設定如下:

(18)

聯立LuGre摩擦模型公式，有:

(19)

(20)

通過系統辨識可得到的控制力為：

(21)

參數辨識誤差為：

e(xd,ti)=u(ti)-u(xd,ti)

(22)

其中，u(ti)為系統輸出的控制力。

取誤差函數的平方和作為目標函數：

(23)

取適應度函數：

(24)

遺傳算法中需要設定的相關參數將在后面的仿真小節中給出，結合上述公式，便可獲得LuGre摩擦模型的動態摩擦參數。

2.4 摩擦補償復合控制

根據LuGre摩擦模型的結構，雖然已由參數辨識獲知模型大部分參數，可不難發現，鬃毛的平均彈性形變量是一階微分方程的未知數，因此該數值是無法直接獲得的。針對鬃毛彈性形變量z設計摩擦力狀態觀測器，從而能夠完整地實現基于模型的摩擦補償控制策略。

摩擦力觀測器數學模型表達如下：

(25)

(26)

(27)

那么：

(28)

對上式兩邊同時積分，有:

(29)

由此可知，式(27)是耗散的。

下面將設計摩擦補償復合控制算法。圖4是泵控缸的簡化傳遞框圖。

圖4 泵控缸傳遞框圖

其中：

G4(s)=βeCts+V0s/[V0mts3+(Ctsβemt+V0Bp)s2+

(30)

令控制器傳遞函數為G1(s)，對伺服電機傳遞函數進行一定程度的簡化，設為G2(s)。令G3(s)=βeDpAp/(Ctsβe+V0s)，圖5為油壓機泵控缸系統摩擦補償位置控制傳遞控制框圖。

圖5 泵控缸摩擦補償位置控制傳遞框圖

根據圖5可得：

(31)

(32)

(33)

聯立上述公式，可得：

(34)

其中，控制器G1(s)選擇常規的PID控制器，通過選取合適的控制器參數，使得G(s)嚴格正實。設G(s)的狀態空間表達式如下：

(35)

e=Cζ

(36)

由于G(s)是嚴格正實的，根據Kalman-Yakubovitvh引理，一定存在矩陣P=PT>0和Q=QT>0，使得：

ATP+PA=-Q

(37)

PB=CT

(38)

≤-ζTQζ

(39)

根據LaSalle定理，可知觀測器誤差和位置誤差會漸進收斂到0，因此該摩擦力觀測器是可行的。

3 摩擦力觀測器的仿真驗證

3.1 靜態摩擦參數

真正的摩擦參數辨識需要由試驗測得的摩擦力與速度的數據進行辨識。首先選取一組較為符合實際工況的摩擦參數，利用MATLAB/Simulink搭建出LuGre靜態摩擦模型，代入一組等時間間隔的速度值，以此求出的摩擦力作為實際摩擦力，從而獲得參數辨識的基礎數據。圖6是MATLAB/Simulink下LuGre靜態摩擦仿真模型，其參數取值如下：

圖6 MATLAB/Simulink LuGre靜態摩擦模型

x1=[Fc,Fs，σ2,Vs]T=[800,1200,20,1.5]T

根據前述辨識手段，對于靜態摩擦模型可以取辨識所需的穩定速度值為從0 mm/s開始，間隔為0.2 mm/s 的等差數列，終止于10 mm/s。除去零點，共50個數值。將相應數值代入摩擦模型，所獲得的仿真理論摩擦力如圖7所示，遺傳代數為n。

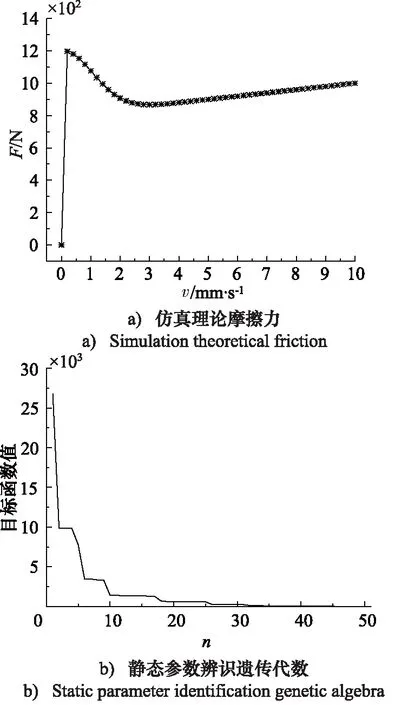
圖7 仿真理論靜態摩擦力與遺傳辨識進化代數

圖8 辨識與理論摩擦力對比

圖9 仿真理論遺傳辨識誤差

3.2 動態摩擦參數

對LuGre摩擦模型進行動態參數的辨識，需要以通過遺傳算法辨識得到的靜態摩擦參數作為整個數學模型的部分參數基礎。模型輸入的速度值取自位速度為y=0.1 sin(0.5πt)正弦曲線，將該組速度值代入圖6所示的MATLAB/Simulink的仿真模型，生成供遺傳算法辨識的理論摩擦力。其中，LuGre動態摩擦模型參數取值如下：

x2=[σ0,σ1]T=[100000,316.2]T

將相應數值代入摩擦模型，所獲得的仿真理論摩擦力如圖10所示。

圖10a和圖10b分別展示了LuGre摩擦模型對滯環摩擦力的準確描述和該模型的鬃毛變化，可以看出LuGre摩擦模型可以較為精確地對摩擦力的復雜特性進行復現。

圖10 仿真理論動態摩擦力

種群及其演化的相關參數設置如下。最大遺傳代數為500，種群個體數目為100，變量數目為4，代溝為0.95，交叉概率和變異概率分別是0.85和0.01。種群生成方式為隨機生成。

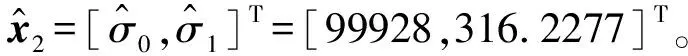
圖11 動態參數辨識遺傳代數

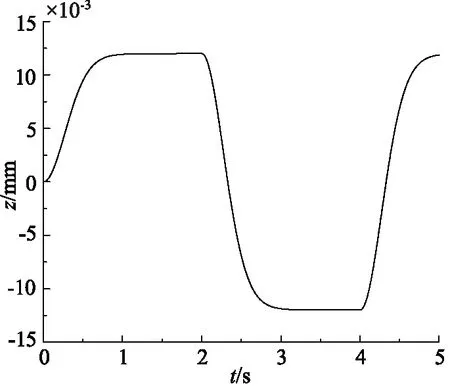
圖12 鬃毛微位移

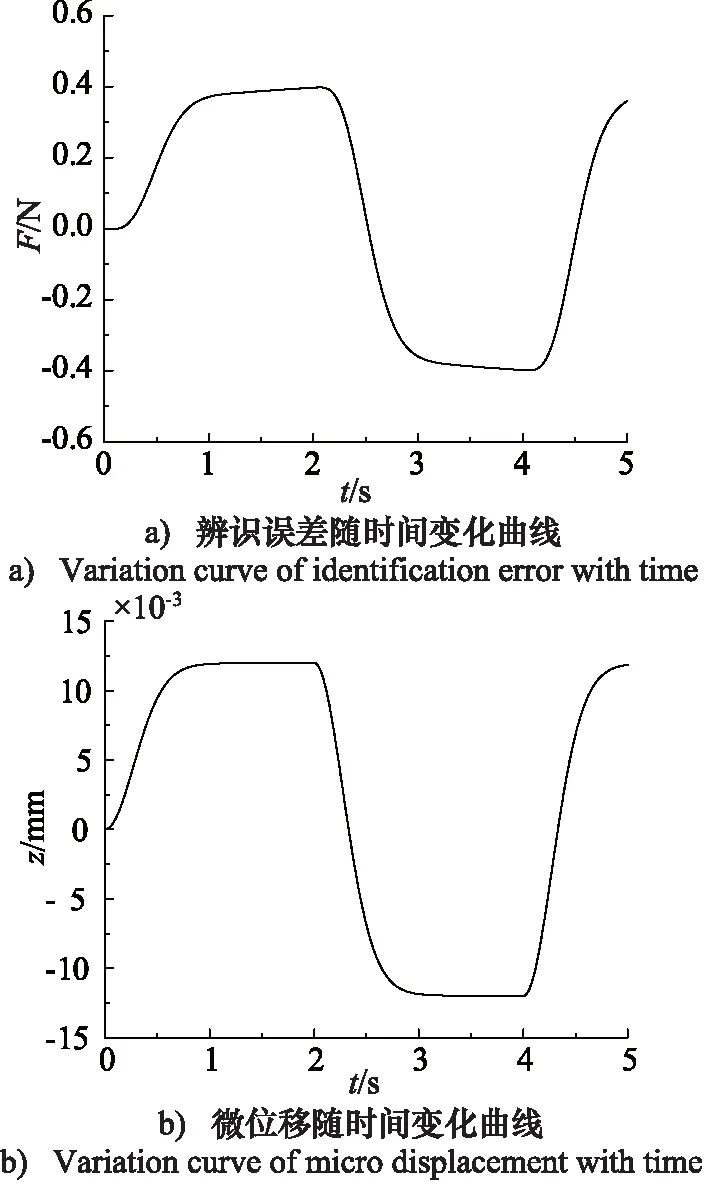
圖13 動態參數辨識誤差

由于實際系統的真實的LuGre摩擦模型的參數未知，本研究通過試驗將遺傳算法辨識得到的實際泵控液壓機位置控制系統的參數對所設計的摩擦力觀測器的效果進行驗證。

4 摩擦力觀測器的試驗驗證

為了驗證設計的摩擦力觀測器的效果，搭建了工業用開式泵控液壓機電液伺服位置控制試驗測試平臺，通過遺傳算法對適用于該測試平臺的LuGre摩擦模型的參數進行辨識。圖15是以圖14為原理圖制成的工業用開式泵控液壓機電液伺服位置控制系統。

1.粗濾油器 2.伺服電機 3.液壓泵 4.伺服驅動器 5.旋轉編碼器 6.單向閥 7.精濾油器 8.溢流閥 9.液壓控制器 10.電磁換向閥 11.平衡閥 12.充液閥 13.壓力傳感器 14.液壓缸(套缸) 15.位移傳感器

圖15 開式泵控液壓機電液伺服位置控制系統

液壓機系統采用某公司研制的HPM01泵控液壓機數控系統。該液壓機數控系統通過Visual Basic編輯用戶界面，并將相關程序內置于觸摸屏。

圖16是試驗測試系統上位機的控制界面，用于辨識靜態摩擦力的參數設置如下：最大遺傳代數為500，種群個體數目為400, 變量數目為4，代溝為0.6，交叉概率和變異概率分別是0.8和0.05。種群生成方式為隨機生成，選擇算子為輪賭盤算子。參數搜索范圍Fc∈[0,1500]，Fs∈[0,1500]，σ2∈[0,100]，Vs∈[0,10]。經過遺傳算法辨識后，LuGre摩擦模型的靜態參數為：

圖16 試驗測試系統上位機界面

x1=[Fc,Fs,σ2,Vs]T=[654.6,1347.6,13.4,1.76]T

圖17a是系統的實際測得的靜態摩擦力和經由遺傳算法辨識得到的模型參數擬合后的靜態摩擦力，圖17b是摩擦力辨識的誤差。

圖17 靜態摩擦力辨識

用于辨識動態摩擦力的參數設置如下，最大遺傳代數為500，種群個體數目為400，變量數目為4，代溝為0.6，交叉概率和變異概率分別是0.8和0.05。種群生成方式為隨機生成。選擇算子為輪賭盤算子。參數搜索范圍Fc∈[0，1500]，Fs∈[0,1500]，σ2∈[0,100]，Vs∈[0,10]。經過遺傳算法辨識后，LuGre摩擦模型的動態參數為：

x2=[σ0,σ1]T=[112610,322.2]T

圖18a是系統的實際測得的動態摩擦力和經由遺傳算法辨識得到的模型參數擬合后的動態摩擦力，圖18b是摩擦力辨識的誤差。

圖18 動態摩擦力辨識

本研究所使用的泵控液壓機電液伺服位置控制系統將液壓缸的行程根據工藝要求劃分為快下運動階段和慢下運動階段，系統的每一運動階段均采用7段S形加減速位移算法。運動行程數值和速度數值可以通過上位機軟件進行設定，加速度數值系統默認與速度值相等。表1所示是系統試驗時的運動軌跡運動表。

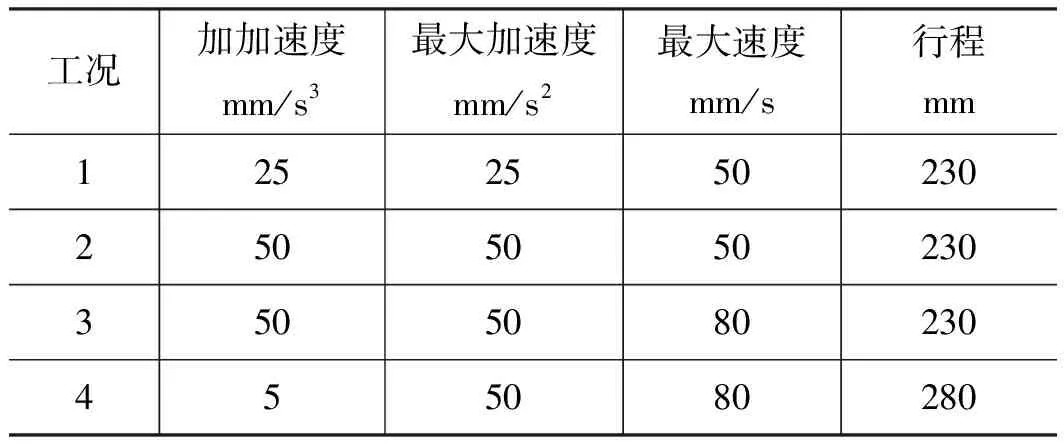
表1 運動軌跡規劃參數表

快下運動階段的控制策略采用PID和基于摩擦力的前饋補償復合控制算法，借助提出的非線性摩擦力觀測器，由此可解決低速階段摩擦力引起的滯后現象并同時提高快下階段的位置跟蹤精度。圖19～圖22所示為系統經過摩擦補償后與常規PID算法下的位置控制性能表現。

圖19 工況1下系統位移及偏差曲線

圖20 工況2下系統位移及偏差曲線

圖21 工況3下系統位移及偏差曲線

圖22 工況4下系統位移及偏差曲線

由圖19～圖22可以看出，采用PID和基于摩擦力的前饋補償復合控制算法后的控制系統在液壓缸快下運動階段的滯后現象得到一定改善，相比未經過補償的快下階段，最大滯后量減少了約40%。后續的運動階段，得到了摩擦補償的系統表現出了良好的位置跟蹤性能，當系統到達目標位置時，超程現象也得到了顯著改善。隨著工況的變化，加加速度、加速度和最大速度提高，系統快下運動階段的位置跟蹤性能依然表現得較為理想。由此可見，泵控液壓機電液伺服位置控制系統快下階段的控制精度經摩擦前饋補償后得到了明顯的提高，證明了辨識出的LuGre摩擦模型對摩擦補償控制的有效性。

5 結論

對廣泛存在于機械系統中的摩擦現象進行了數學模型化分析，討論并分析了摩擦模型的數學特性。以能夠較為全面描述摩擦現象豐富特性的LuGre摩擦模型為基礎，通過遺傳算法對模型的6個未知參數進行識別，于此基礎上提出了一種非線性摩擦力觀測器，并對遺傳算法的有效性和LuGre摩擦模型的效果進行了驗證。仿真結果表明，遺傳算法下的LuGre摩擦模型中，靜態摩擦力的辨識值十分接近理論靜摩擦力數值，動態摩擦力的復雜特性得到了較為精確的復現；試驗結果也證明了參數辨識的有效性與非線性摩擦力觀測器的效果。