閉式泵控新型液壓-機械執行器位置控制特性

倪 豪，葛 磊，權 龍，趙 斌

(太原理工大學 機械與運載工程學院，山西 太原 030024)

引言

傳統的液壓系統以閥控系統為主，但閥控系統存在節流損失和溢流損失，其效率低下，另外還存在容易受到油液污染等缺點[1]。在提倡節能減排的社會背景下，國內外學者就如何提高液壓系統的效率、發展綠色節能的新技術做了大量研究[2-3]。

王棟梁等[4]提出了非對稱閥控非對稱缸的概念，并對其動靜態特性進行了分析，但非對稱閥控系統的控制理論發展的并不完善，控制過程相對復雜。另外許多學者提出采用閉式泵控系統取代閥控系統，其中閉式泵控非對稱液壓缸存在流量不匹配的問題，權龍教授[5-9]設計了多配油窗口的非對稱軸向柱塞泵，通過改變配油盤的配油比來平衡不對稱的流量，節能效果明顯。馬艷斌等[10]提出一種變轉速定量泵-變量泵結合的閉式泵控系統，通過控制變量泵的排量來匹配單出桿液壓缸兩腔的不對稱流量。吳曉明教授[11]提出了四腔液壓缸的原理，通過將活塞桿做成空腔兼做另一缸體的形式，把普通的兩腔室液壓缸做成具有4個腔室的液壓缸，總結出四腔液壓缸具有節省空間、有效降低系統的壓力波動、提高工作效率、改善工作環境等優點。KUMAR H等[12]自主設計了一種帶有電液補償器的軸向柱塞泵，顯著提高了系統的效率。

上述研究主要是針對液壓系統自身進行的優化與創新，還有一種研究趨勢是采用電驅系統或電液混合驅動系統代替傳統的液壓系統[13-15]。其中，電動缸憑借其體積小、效率高、定位精度高、節能環保無污染等優點，近年來在一些輕載場合已經逐漸取代了液壓缸系統[16-17]。權龍教授團隊[18]提出以電動缸為主、液壓缸-蓄能器組合為輔的液電混合動臂驅動方案，該方案顯著提高了挖掘機舉升系統的能量利用效率。孟平等[19]將電動缸應用于電鏟登機梯升降系統，極大減小了系統故障發生的頻率。鄧琦[20]指出行星滾珠絲杠電動缸具有大承載、耐沖擊等優點，將來會在航空航天、武器裝備等領域獲得廣泛的關注。

電動缸技術固然發展較快，但是其依然存在功重比低于液壓系統的問題，因此電動缸在低速重載場合的應用受到了一定限制。為解決上述問題，充分發揮液壓系統與電動缸系統的優勢，提出采用閉式泵控液壓馬達代替電動機驅動滾珠絲杠的方案，并對其位置控制特性進行了仿真研究。

1 系統的工作原理

系統主要由電液比例變量機構、變量泵-定量馬達系統、減速器裝置以及滾珠絲杠組成，圖1為閉式泵控新型液壓-機械執行器系統原理圖。

1.變量泵 2.單向閥 3.蓄能器 4.溢流閥 5.定量馬達 6.絕對值編碼器 7.同步帶式減速器 8.螺母 9.滾珠 10.絲杠 11.活塞桿 12.變量缸 13.比例換向閥

該系統通過比例換向閥13來控制變量缸12，變量缸12的活塞桿控制變量泵1斜盤傾角來改變排量，進而控制定量馬達5的轉速，改變變量泵1斜盤傾角的方向便可以改變定量馬達5的旋轉方向。以活塞桿阻抗伸出工況為例，定量馬達5通過同步帶式減速器7將轉矩傳遞給絲杠10，由于絲杠10被固定，所以其只能繞軸線方向做旋轉運動，而不能向右移動。這樣，滾珠9會沿著絲杠10的螺紋向前運動，進而帶動螺母8向右做直線運動，從而達到使活塞桿伸出的目的，滾珠絲杠的內部結構如圖2所示。絕對值編碼器6安裝在減速器的高速軸上，可以實時檢測馬達的轉角以及轉速。

圖2 滾珠絲杠內部結構圖

2 系統的數學模型

以電信號為輸入，比例方向閥位移為輸出的傳遞函數為：

(1)

式中，xv——比例方向閥閥芯位移

I——比例方向閥輸入電流

Kbv——閥芯位移增益系數

ωbv——液壓固有頻率

ξbv——閥的阻尼比

以閥芯位移為輸入，變量缸的活塞桿位移為輸出的傳遞函數為：

(2)

式中，xp——變量缸活塞桿的位移

ωp——缸的液壓固有頻率

ξp——缸的阻尼比

Kq——閥的流量增益

Ac——液壓缸有效面積

變量泵斜盤傾角與變量缸活塞桿位移的關系為：

xp=L·γ

(3)

式中，L——變量活塞油缸施力點與斜盤鉸接點間的距離

γ——斜盤傾角，因為γ很小，故sinγ≈γ

則從液壓缸活塞位移到泵的斜盤傾角之間的傳遞函數為：

(4)

式中，Kφ——變量泵斜盤傾角系數

變量泵的排量方程為：

Vp=Kpγ

(5)

式中，Vp——變量泵的排量

Kp——變量泵的排量梯度

變量泵流量Qp連續性方程：

Qp=Vpωpn-Cip(ph-pr)-Cepph

(6)

式中，ωpn——變量泵的輸出角速度

Cip——變量泵的內泄漏系數

Cep——變量泵的外泄漏系數

ph——變量泵高壓側壓力

pr——變量泵低壓側壓力

變量泵低壓側的流量即系統的補油流量，通常視為常數，將式(5)代入式(6)，對其進行拉氏變換可得：

Qp(s)=Kqpγ(s)-Ctpph(s)

(7)

式中，Kqp——泵的流量增益，Kqp=Kpωp

Ctp——泵的總泄漏系數，Ctp=Cip+Cep

液壓馬達的高壓側流量Qm連續性方程：

(8)

式中，Cim——液壓馬達的內泄漏系數

Cem——液壓馬達的外泄漏系數

Vm——液壓馬達的排量

θm——液壓馬達的轉角

V0——變量泵和液壓馬達工作腔及連接管道的總容積

βe——油液有效體積的彈性模量

將式(8)拉氏變換可得：

(9)

式中，Ctm為馬達的總泄漏系數，Ctm=Cim+Cem。

滾珠絲杠折算到液壓馬達輸出軸上的的轉動慣量Js：

(10)

式中，Lb——絲杠的導程

ρ——絲杠的密度

r——絲杠的半徑

大帶輪折算到馬達輸出軸上的轉動慣量J1：

(11)

式中，m1——大帶輪質量

D1——大帶輪外徑

d1——大帶輪內徑

i——速器傳動比

同步帶小帶輪的轉動慣量J2：

(12)

式中，m2——小帶輪質量

D2——小帶輪外徑

d2——小帶輪內徑

活塞桿軸向力在馬達的輸出軸上產生的轉矩TL為：

(13)

式中，F——活塞桿推力

η——滾珠絲杠副的傳遞效率

μ0——預壓螺母內部的摩擦系數

F0——滾珠螺母預壓載荷

Pb——絲杠導程

液壓馬達輸出軸上的力矩平衡方程：

(14)

式中，p1——馬達高壓側壓力

p2——馬達低壓側壓力

Jm——液壓馬達的轉動慣量

Bm——絲杠、負載、馬達等折算到液壓馬達輸出軸上的總黏性系數

G——系統各部分折算到馬達軸輸出軸上的總剛度

對式(14)進行拉氏變換可得：

Vmph(s)=(Js2+Bms+G)θm(s)+TL

(15)

式中，J——系統折算到馬達軸上的總轉動慣量

J=Jm+J1+J2+Js

活塞桿的位移x與馬達轉速的關系方程：

(16)

式中，Kbh為絲杠位移增益，Kbh=Pb/(2πi)，對上式進行拉氏變換可得：

x(s)=Kbhθm(s)

(17)

聯立式(7)、式(9)、式(15)以及式(17)，阻尼系數等于Vm/Ct，Ct為泵和馬達的總泄漏系數，因阻尼系數通常比Bm大的多，故不考慮Bm，并忽略剛度的影響，即G=0，則消除中間變量可得：

(18)

圖3為系統完整的閉環傳遞函數框圖。

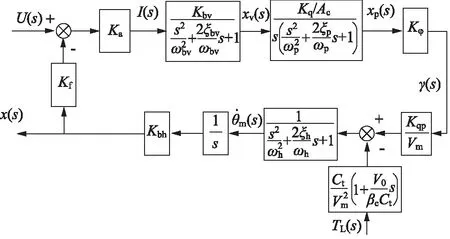
圖3 系統的閉環傳遞函數框圖

圖3中，Ka為比例方向閥電流增益，Kf為反饋系數。對整個系統而言,電液比例部分的諧振頻率遠高于后續環節,故可將該部分的傳遞函數簡化為比例環節，從而可以得到以電信號為輸入，活塞桿位移為輸出的系統閉環傳遞函數為：

(19)

3 系統的閉環位置控制特性動態仿真

系統的閉環控制原理圖如圖4所示。絕對值編碼器用來檢測馬達轉過的角度，馬達的轉角對應著活塞桿的不同位置，將其與目標位置對比，便可得到偏差信號。偏差信號經PID處理以后作用于系統。

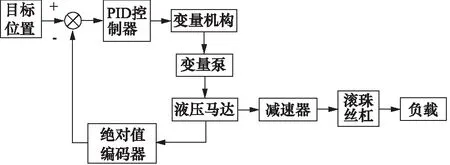
圖4 系統控制原理圖

為了驗證閉式泵控新型液壓-機械執行器系統的動態位置控制特性，在SimulationX里建立了該系統的仿真模型，其中，電液比例變量機構用其簡化后的傳遞函數代替物理模型，仿真模型如圖5所示，仿真過程中系統的主要參數見表1。

表1 仿真模型參數表

圖5 系統仿真模型

仿真時系統的外負載力為阻力，大小為20 kN，其方向不發生改變，為常值載荷。變量泵與定量馬達的機械效率、容積效率均為0.9。系統在上述參數下運行仿真，結果如下。

3.1 系統的時域分析

(1)輸入信號為階躍信號，1 s時目標位置上升到100 mm，PID控制器的參數如下：Kp=20，Ti=200，Td=0.052，活塞桿的位置仿真曲線如圖6所示。

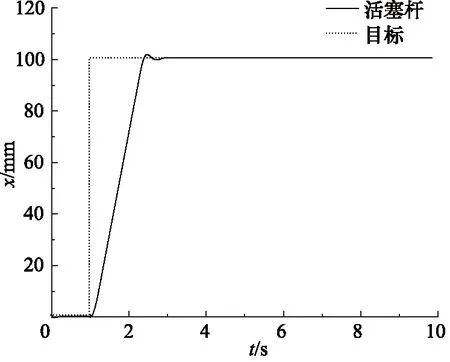
圖6 階躍信號下活塞桿的位置響應曲線

從圖6中可以看出，系統響應迅速、平穩，上升時間大約為1.4 s，系統在經歷了短暫振蕩以后立即恢復穩定狀態；系統的超調量較小，最大超調為1.28 mm，約為穩態值的1.3%；穩態誤差幾乎為0。

(2)比例系數Kp和微分常數Td等其他參數不變，積分時間常數Ti分別取0，10，50，200時，系統的階躍響應曲線及誤差曲線的局部放大圖分別如圖7、圖8所示。

圖7 不同積分時間常數下的階躍響應曲線

圖8 不同積分時間常數下的誤差曲線

仿真曲線表明，系統在負載的作用下僅通過PD控制無法消除穩態誤差，PID控制器的積分項有利于消除穩態誤差，但是對于該系統而言，積分時間常數過小及積分作用過強，會增大系統的超調量，延長系統的調整時間。適當增大積分時間常數能夠降低超調量，減小穩態誤差，提高系統的穩態精度。

(3)輸入信號更改為正弦信號，PID的參數與(1)中一致(下同)，其頻率設置為0.1 Hz，幅值為50 mm，系統的位置響應曲線如圖9所示。

圖9 正弦信號頻率為0.1 Hz時活塞桿的位置響應曲線

從圖9中可看出，系統響應平穩，活塞桿的位置曲線變化平緩，幾乎無超調，能夠很好地跟蹤正弦信號的變化。

3.2 系統的頻域分析

為了得到系統的頻域特性，使用50個不同頻率的正弦信號對系統進行激勵。將輸入正弦信號的幅值設置為50 mm，頻率從0.02 Hz均勻增加到1 Hz，依次將SimulationX中的仿真結果進行數據保存，由于SimulationX仿真環境在針對系統動力學方程進行求解時，為提高求解效率使用變步長的數值解法，采樣時間不滿足線性增加的要求，故需要對信號進行均勻化處理，方法是利用SimulationX中的cruve set模塊，將保存后的數據導入該模塊中，修改SimulationX軟件的計算步長，將其最大步長設為定值，運行仿真，將處理后的數據導入MATLAB并采用FFT頻譜分析法，然后求得的系統位置閉環伯德圖如圖10所示。

圖10 系統位置閉環伯德圖

將系統的最大跟蹤頻率定義為幅值衰減3 dB或系統的相位滯后90°。從圖10中可以看出，隨著正弦信號頻率的增加，系統的幅值衰減速度要快于相位滯后速度，因而該系統的最大跟蹤頻率由幅頻特性決定，約為0.52 Hz，此時信號衰減3 dB，即系統帶寬約為0.52 Hz。

3.3 系統抗負載干擾能力分析

輸入信號仍然為階躍信號，此時加入圖11所示的隨機性負載干擾，在面對隨機性負載干擾的情況下，活塞桿的位置仿真曲線如圖12、圖13所示。

圖11 隨機性負載干擾曲線

由圖12可以看出，當輸入信號為100 mm的階躍信號時，系統的上升時間幾乎不受隨機性負載干擾的影響，大約為1.4 s；活塞桿到達目標位置后，在負載的擾動下，系統會在目標位置附近振動，但振幅不超過2 mm。當系統的輸入信號為正弦信號時，系統的閉環位置響應曲線與目標位置曲線較為吻合，振幅較小，如圖13所示。

圖12 階躍信號下系統的抗負載干擾特性曲線

圖13 正弦信號下系統的抗負載干擾特性曲線

上述仿真結果表明，閉式泵控新型液壓-機械執行器系統的閉環位置控制特性受負載干擾的影響較小，系統穩定時，面對負載的隨機變化，表現出了良好的抗負載干擾能力。

4 結論

提出了閉式泵控新型液壓-機械執行器系統，并推導了其數學模型，通過數學模型與仿真實驗，研究了該系統的閉環位置控制特性，結論如下：

(1)新系統響應迅速、平穩，系統在100 mm的階躍信號下，經歷約1.4 s的時間上升到穩態位置，超調量為1.28 mm；系統在經歷短暫振蕩后立即恢復穩定狀態，通過調整PID的參數可以幾乎完全消除穩態誤差;

(2)系統的頻域分析結果表明，該系統在正弦信號頻率增大時，幅值的衰減速度快于相位滯后速度。當輸入正弦信號的幅值為50 mm時，系統的帶寬為0.52 Hz；

(3)在隨機性負載干擾的作用下，系統響應平穩、振蕩較小，振幅不超過2 mm，這表明系統具備良好的抗負載干擾能力。