高中數學復習課六環節教學模式及實施策略

河北省唐山市遷安市第四高級中學（遷安市第一中學西校區）黑麗麗

復習課是高中數學課的主要課型之一，是夯實雙基，拓展知識，總結規律，培養解題能力的主戰場。如何上好復習課，下面我從六環節教學模式解讀利用向量解決三角形問題。在高考中，解三角形是重要題型，通常要和向量結合考查，今天我們就是要探索在我校推動的六環節教學模式下如何利用向量法探究三角形的中線、角平分線問題，抓住三角形“三線”及“四心”，能巧妙解決問題，并形成數學建模思想展開教學的。

一、導（情境導入）

復習課的導入要切入點準確，啟發性強，“一針”即入本節課重點，迅速喚醒學生的思維，有情有境，情，就是利用老師的激情和對于問題深入理解和參悟去喚醒和激發學生的學習激情。境，就是教師要設計合理的境況，引發學生的思考，比如利用合理的考題或者是課本的習題設計情景，讓學生感受到自己知識的不足，利用自己已經學過或掌握的知識不能很好的解決考題中的涉及本節課內容的問題，需要對知識進行再理解再認識才能解決問題，激發學生的學習興趣和動力。然后才能高效的完成一節課的學習。

本節情景導入：在大屏幕上提出問題：三角形的“中線、角平分線”的向量表示是什么？

在三角形中，中線：

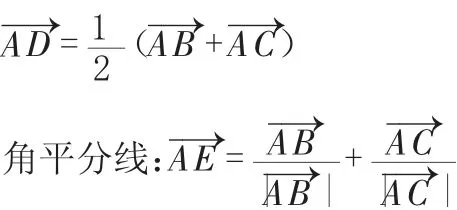
緊抓符號與圖形，讓學生深刻理解三角形的中線與角平分線的向量法表示。

二、標（目標展示）

即通過本節課學習一定要完成的任務和達到的要求。這個環節應該在情境導入的環節之后馬上給出，使學生清楚地知道學習重點、難點，為下面幾個環節確定好方向，增強教學的目的性，有的放矢。這個目標可以設計在課件和學生的預習案上，比如本節課復習的內容應當掌握的程度，學生應當掌握的技能與方法，寥寥幾筆就可說明，不宜過長。

本節目標為：

1.通過向量法研究三角形的性質。

2.以三角形為研究對象，從向量角度對其性質再研究。

三、自（自學感知）

是在教師的指導下，學生帶著問題，進行分析、理解、尋找重點、難點和發現其他問題的過程，是課堂教學“動靜結合”中靜的體現，是自主學習的環節，更是學生獨立認知、思考的過程。這個環節依據復習內容的特點應該有這樣幾種處理方式：如果基礎知識比較多，就可以設計一個預習案，將基礎知識以填空的形式或問題的形式先發給學生，讓學生課前預習，課前預習的預習案最好能收上來查看一遍，看學生的填寫情況或回答情況，課上做到有針對性的講解；如果基礎知識比較少，就可以以填空或小問題的形式出現在學案，利用課上的時間進行自學，然后教師展示答案，學生進行對照，對不能明白的共性問題教師加以點撥。

本節自學感知：

問題探究：已知O是平面內一定點，A、B、C是平面上的不共線的三個點，動點P滿足，且λ∈[0，+∞），則點P的軌跡一定通過△ABC的（）。

A.內心B.外心C.重心D.垂心

變式：已知O是平面內一定點，A、B、C是平面上的不共線的三個點，動點P滿足，且λ∈[0，+∞），則點P的軌跡一定通過△ABC的（）。

A.內心B.外心C.重心D.垂心

此變式題恰巧就是對三角形角平分線的考查，角平分線的交點即為三角形的內心。

四、合（合作展評）

是學生之間釋疑解惑的過程，是學習團隊精神的體現，是學生在平等的基礎上，互補、幫扶學習的有效途徑。這個步驟除了生生合作，還要有師生合作，教師及時地對討論的疑難問題進行啟發、點撥，對各小組展示中存在的問題給予糾正，對發散思維的訓練給予誘導、啟發。這一環節是教學的中心環節，也是新課改理念的體現之處。在這里學生之間會有思想碰撞，教師和學生之間也會有思想碰撞。這里的展評，就可以小組展示并講解，其他小組給予評價與補充。也可以是教師的講解，最后師生達成共識，使知識得以升華。這樣學生得到的知識才是自己的知識。這里最害怕的是走過場，不是真合作不是真探究。當然可以根據課的特點，有可探究的問題就探究合作，沒有合適的問題就可以采用更合理的方式進行代替，不能千篇一律，最終的目標是為了讓學生形成知識體系。

本節合作展評

例1在△ABC中，a，b，c分別是內角A、B、C所對的邊，且滿足

（1）求角B的值；

（2）學生會有不同做法，讓學生展開思路，對比優劣。

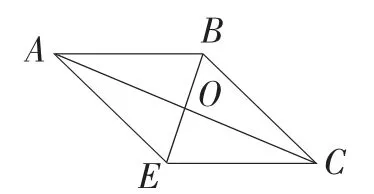
法一：補成平行四邊形（中線）延長BO到E，使BO=OE，則四邊形ABCE為平行四邊形。

得a=1.

這是一種很不錯的方法，緊抓向量加法的平行四邊形法則。

法二：利用向量法表達三角形中線，即中線定理。

∴a2-2a+1=0，∴a=1.

法三：由下圖在△BOC中和△BOA中分別利用余弦定理解三角形，再由∠BOC+∠BOA=π，則cos∠BOC=-cos∠BOA，即可解出來，但計算量大，較麻煩。此方法學生想出來的較多，但大部分學生算不出來。教師要針對這種情況做出指導，指出這是一種重要方法，有時做題必須用這種思想。

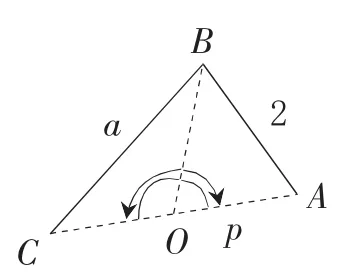
練習1：△ABC內接于半徑為R的圓，a，b，c分別是內角A、B、C所對的邊，且2R（sin2B-sin2A）=（b-c）sinC，c=3.

（1）求∠A的值；

五、歸（歸納拓展）

是對本節課的重點、難點問題的解決方法或易錯、易混淆的地方歸納、總結、強調，而且通過強化訓練對所學的知識、方法加以鞏固。這個部分最好采用例題的方式進行完成，選定符合本節知識的例題進行知識點的總結和分析問題解決問題方法的升華。例題的選擇一定要典型性和代表性，可以是模擬試題也可以是高考試題，最好是經過加工或改編的試題，功能性要強，一般是2~3個選擇題或一個大題。主要是通過例題歸納分析問題的思路和解決問題的方法，目標是形成方法體系，把知識講明白，讓學生領悟透。

本節歸納拓展設置為：

例2已知在△ABC中，a，b，c分別是內角A、B、C所對的邊，sinA=2sinC，2b=3c。

（1）求cosC；

分析：（1）由正弦定理和余弦定理易得出。（2）由角平分線性質：=2.

這類問題重點指導學生緊抓三角形角平分線的性質結合向量的模表達出來，使解題更加輕松。

六、測（達標檢測）

是對本節課的學習內容進行測試，是檢驗課堂效率高低的重要一環，試題內容緊扣學習目標，要具有針對性、科學性，為評價的準確提供保證。這部分根據以上幾個環節的時間來確定，如果以上都能在規定的時間完成的話，可以幾個選擇題或一個大題讓學生體會學過的知識和方法，特別是例題所體現的方法的應用，讓學生體會到學習方法前后解題的速度變化，體會到學習方法是有用的，學生才愿意學，才能達到教學的最佳境界。

本節達標檢測設計為：

A.三邊均不相等的三角形

B.直角三角形

C.等腰非等邊三角形

D.等邊三角形

2.在△ABC中，a，b，c分別是內角A、B、C所對的邊，且滿足2sinBcosA=sinA cosC+cosAsinC。

（1）求∠A的值；

（2）若b=2，c=1，D為BC的中點，求AD的長。

3.在△ABC中，D為BC上的點，AD平分∠BAC，△ABD面積是△ADC的2倍。

以上，以實例論述了六環節教學模式在數學復習課課堂上的具體應用及原理的剖析，教學環節為：導（情境導入）—標（目標展示）—自（自學感知）—合（合作展評）—歸（歸納拓展）—測（達標檢測），在實踐中取得了良好的效果。總之，不同的教學策略會從不同角度來激發學生的學習欲望，使學生的學習潛能得到充分的挖掘，促進學生主動在課堂上分析問題、解決問題，實現學生學習能力的提高和個性的發展，進而實現有效學習和高效課堂。