基于GWO-SPA和MSE的往復壓縮機氣閥故障特征提取方法

潘云杰，李穎，吳仕虎，陳佳文

(沈陽理工大學機械工程學院，遼寧沈陽 110159)

0 前言

往復壓縮機作為石油、化工等領域的重要大型設備，其結構復雜，零件眾多，致使往復壓縮機檢修極其困難；同時，往復壓縮機一旦發生故障，將會導致工業生產的停止，降低生產效益，因此，對往復壓縮機故障進行研究具有重要的實際意義。通過查閱往復壓縮機相關資料及對實際的往復壓縮機進行研究發現，往復壓縮機的氣閥故障是造成往復壓縮機不能正常運行的重要因素之一。

往復壓縮機氣閥在工作中會受到周圍環境及摩擦、沖擊等因素的干擾，導致其振動信號具有強烈的非線性、非平穩性特征。為此，首先對氣閥振動信號進行自適應分解，消除振動信號中所摻雜的其他因素的影響，以提取出氣閥振動信號中能反映氣閥工作狀態的特征信號。往復壓縮機氣閥振動信號的非線性特征，導致傳統的線性信號分析方法不再適用。近年來，許多非線性信號分析方法得到了迅速發展，其中較為典型的有小波分析、EMD、LMD、VMD等。雖然這些方法均得到了有效的應用，但是以上方法均會受到多個參數和分解的分量個數的影響，分量選取過多容易產生過擬合，分量選取過少不能完整地概括信號的所有特征。針對上述問題，本文作者采用SPA方法對往復壓縮機氣閥振動信號進行自適應分解，該方法的優點在于算法簡單高效，且由于將信號分解為趨勢項和去趨勢項兩項，因此可以避免因分量選取問題對分解結果的影響，同時因為影響SPA分解好壞因素僅有正則化參數，所以只需要一個參數就可以對信號進行有效的自適應分解。

對信號進行自適應分解后，再對其進行定量分析以提取信號中的特征。熵能反映信號的復雜性及隨機性，深層次地提取隱藏在信號中的動態特征，因此被廣泛應用于故障診斷領域。目前較為常用的有近似熵、樣本熵、排列熵等。單一尺度的熵值有時不能完全反映信號的特征，因此又提出多尺度熵的方法，如多尺度排列熵、多尺度樣本熵等。

基于以上分析，本文作者提出一種新的基于灰狼算法優化平滑先驗分析、結合多尺度樣本熵的往復壓縮機氣閥故障特征提取方法。利用灰狼算法對SPA的參數進行尋優，將尋優后的參數代入SPA中對往復壓縮機氣閥處振動加速度信號進行自適應分解，得到信號的趨勢項和去趨勢項，然后分別求取去趨勢項數據的多尺度樣本熵均值和偏度的平方，結合多尺度樣本熵的均值和偏度的平方作為往復壓縮機氣閥信號的特征向量輸入支持向量機中進行訓練與測試。通過實驗分析可知，文中提出的方法可以有效提取往復壓縮機氣閥的故障特征，并實現故障類型的準確區分。

1 灰狼-平滑先驗分析(GWO-SPA)

1.1 SPA方法

平滑先驗分析(SPA)方法由KARJALAINEN博士提出，可以有效地分解出信號的去趨勢項和趨勢項。相較于傳統的最小二乘估計，SPA方法采用了一種更為通用的參數估計方法：正則化最小二乘法。SPA算法具體原理如下：

原信號設為，趨勢項設為，搭建趨勢項的線性觀測模型。

=+

(1)

式中:為觀測矩陣；為回歸參數;為觀測誤差。

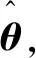
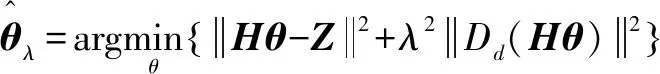
(2)

式中:為正則化參數;為第階微分算子的離散形式表達。

設有個局部極值點

=[,,…,]

(3)

推導得式(3)中任意階趨勢為

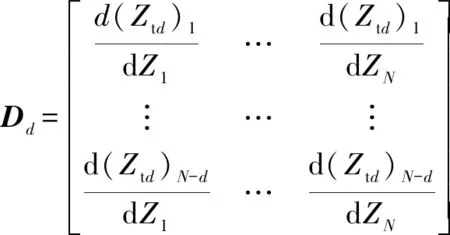
(4)

使微分項()趨于0，則式(2)可表示為

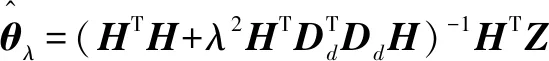
(5)

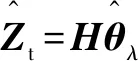
(6)

為簡化趨勢項的計算，設為單位矩陣。同時設置為2階，如式(7)所示:

(7)

去除原信號的趨勢項后，得到去趨勢項如式(8)所示:

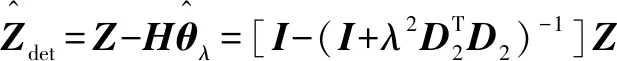
(8)

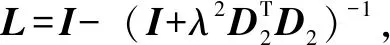
1.2 GWO-SPA

通過上述分析可知，影響SPA分解好壞的因素只有正則化參數，因此，有必要對參數進行優化分析，選擇合理的數值。灰狼(Grey Wolf Optimization，GWO)算法于2014年首次被提出，該算法有較強的收斂能力和全局搜索能力，同時具有參數少和易于實現的優點。故文中引入GWO算法對SPA方法的參數進行尋優處理，具體步驟如下：

(1)確立需要優化的參數及參數取值范圍，文中參數為SPA方法中的正則化參數，取值范圍1≤≤20；

(2)初始化灰狼種群及3只頭狼的位置；

(3)對輸入的信號序列進行SPA分解；

(4)確立適應度函數，文中為多尺度樣本熵的均值和偏度的平方，取適應度函數的最小錯誤率為優化目標；

(5)對SPA分解后的信號計算適應度函數值，并判斷是否達到優化目標。若達到，輸出參數的最優解；若沒有達到，更新灰狼的個體適應度及灰狼的位置，并重復步驟(3)、(4)，直到達到優化目標為止。

將尋優后的參數代入SPA中對往復壓縮機氣閥振動加速度信號進行自適應分解。

1.3 仿真分析

為驗證文中所提方法能夠有效提取出氣閥振動信號的特征信號，構造仿真信號進行分析。仿真信號如式(9)所示：

=sin(2π/30)+2sin(2π/50)++

(9)

其中：為隨機噪聲；為高斯白噪聲。采集5 000個數據點進行分析，仿真信號時域圖如圖1所示。

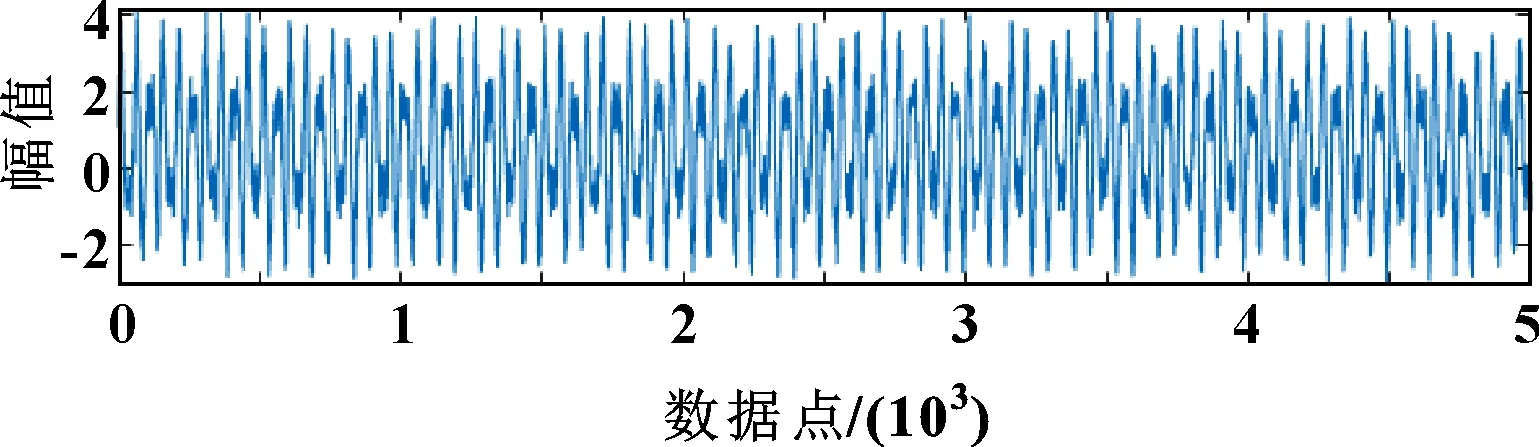
圖1 仿真信號

對仿真信號進行SPA分解，分解結果如圖2所示。

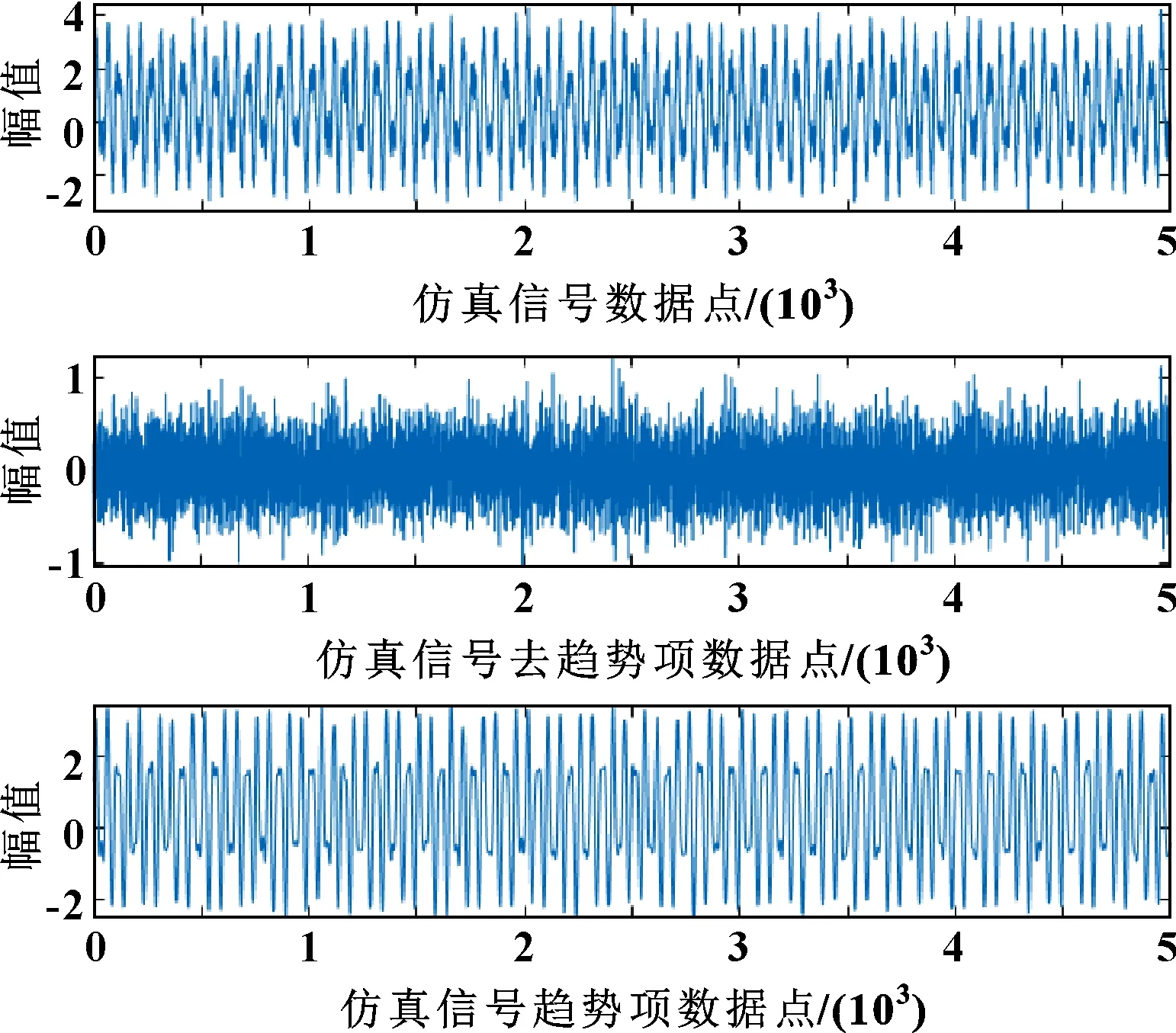
圖2 SPA分解結果

由圖2可以看出：利用SPA對仿真信號進行自適應分解后，趨勢項和去趨勢項有明顯的區分,趨勢項保留了原始信號序列的物理性質，去趨勢項數據保留了噪聲、故障等信息成分,證明了文中所提方法的有效性。氣閥在工作時測得的原始信號的物理性質即為往復壓縮機運行時由于內外壓力不同而傳給氣閥的振動信號，不同狀態氣閥的信號其物理性質幾乎相同。氣閥在發生故障時，其振動信號的改變主要體現在去趨勢項數據所反映的沖擊特性上，故利用去趨勢項數據來判斷氣閥是否存在故障以及故障類型。

2 多尺度樣本熵(MSE)基本原理

熵通過反映信號的復雜性及隨機性而提取出信號的特征，但有時單一尺度的熵并不能完全提取信號的特征，因此文中引入多尺度樣本熵對往復壓縮機氣閥信號進行分析。

2.1 樣本熵

針對時間序列()(=1,2,3，…，)，樣本熵計算步驟如下：

(1)利用嵌入維數對時間序列構建維矢量:

()=[(),(+1),…,(+-1)]

(10)

式中:=1,2,…,-+1。

(2)定義()和()之間對應元素最大距離為

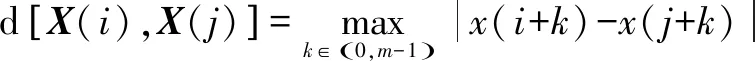
(11)

式中:=1,2,3,…,，且≠。

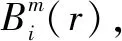
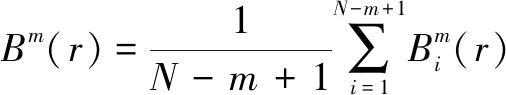
(12)

(4)在維數+1下，重復步驟(1)(2)(3)得到+1()。

(5)定義樣本熵為

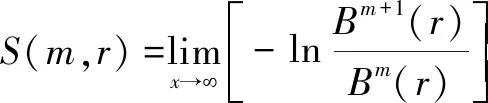
(13)

(6)當時間序列為有限值時，則樣本熵估計值為

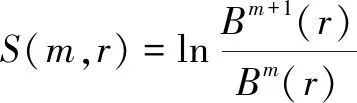
(14)

2.2 多尺度樣本熵(MSE)算法

根據樣本熵原理，多尺度樣本熵的計算步驟如下：

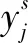
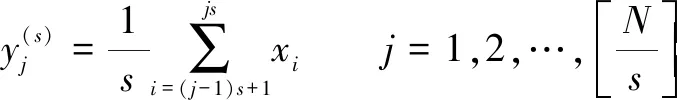
(15)

式中：代表尺度因子。

(2)對每個粗粒化序列求解樣本熵值，將樣本熵值進行歸一化處理即得到多尺度樣本熵。

根據上述分析可知，影響多尺度樣本熵的參數主要有尺度因子、相似容限、嵌入維數三個參數。相似容限通常選擇=0.1～0.25，其中為時間序列的標準差。由于對信號求解結果影響不大，故在文中，選擇為0.15，同時選擇合理的區間，分別求取氣閥不同狀態去趨勢數據信號在不同嵌入維數和尺度因子下的MSE熵值的均值，來確定和的取值。

3 基于GWO-SPA和MSE的往復壓縮機氣閥故障特征提取方法

3.1 方法步驟

綜上所述，文中提出的基于GWO-SPA和MSE的故障特征提取方法，具體步驟如下：

步驟一，利用實驗室往復壓縮機實驗平臺分別模擬氣閥正常運行、閥片斷裂、閥有缺口、閥少彈簧時的運行狀態，搭建信號采集系統，采集往復壓縮機氣閥4種狀態下的振動加速度信號。

步驟二，以多尺度樣本熵均值和偏度的平方作為適應度函數，利用灰狼算法對SPA的參數進行尋優，將尋優后的參數代入SPA中對往復壓縮機氣閥處振動加速度信號進行自適應分解。

步驟三,選擇合適的嵌入維數以及尺度因子的區間，利用尺度因子對往復壓縮機氣閥振動加速度信號分解后得到的去趨勢項數據進行粗粒化處理，然后對不同尺度下的粗粒化序列求解樣本熵值，并將樣本熵值進行歸一化處理，即得到往復壓縮機氣閥去趨勢項數據的多尺度樣本熵。

步驟四,分別求解往復壓縮機氣閥4種狀態下去趨勢項數據的多尺度樣本熵的均值MSE和偏度的平方MSE，結合構成往復壓縮機氣閥的特征向量=(MSE,MSE)。

步驟五，分別將往復壓縮機氣閥4種狀態下的特征向量及對應的標簽輸入至SVM，進行故障的識別。流程圖如圖3所示。

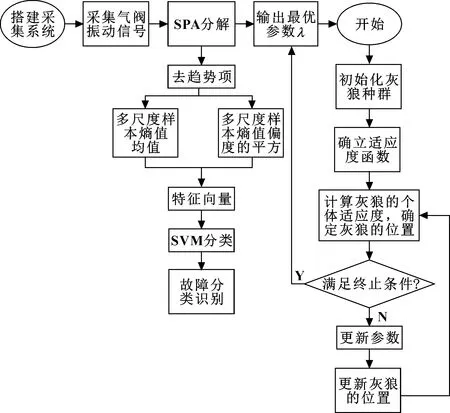
圖3 基于GWO-SPA和MSE的故障特征提取方法流程

3.2 往復壓縮機氣閥故障特征提取

文中壓縮機選用實驗室現有的2D-90MG往復壓縮機，生產能力排氣量為90 m/min，排氣壓力為0.15 MPa，設置采樣頻率為50 kHz，采集時間為4 s。往復壓縮機實驗平臺如圖4所示。

圖4 往復壓縮機實驗平臺

信號采集系統使用實驗室現有的東華振動加速度傳感器和NI9231振動信號采集卡，結合LabVIEW軟件進行搭建。搭建的LabVIEW軟件信號采集系統后面板如圖5所示。

圖5 信號采集系統后面板

分別模擬氣閥正常運行、閥片斷裂、閥有缺口、閥少彈簧時的運行狀態，其中閥有缺口為中間閥片有2個缺口；閥少彈簧狀態為在正常狀態(6個彈簧)下拿走2個彈簧；閥片斷裂為閥片從中間斷裂。取往復壓縮機氣閥4種狀態下的樣本各40 組，每組點數6 048個點，總計160組數據。往復壓縮機氣閥4種狀態下的振動加速度信號如圖6所示。

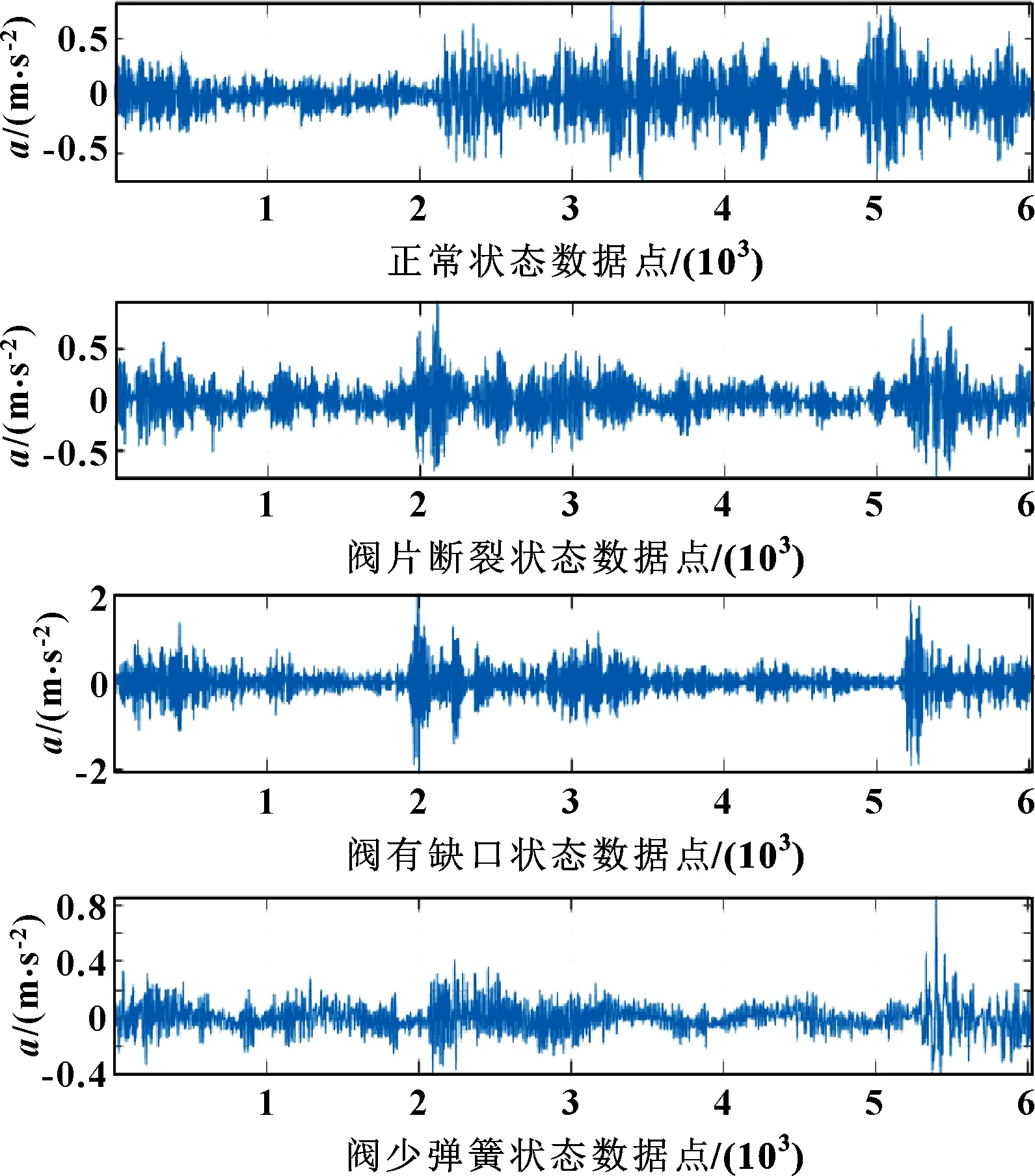
圖6 往復壓縮機氣閥各種狀態下的數據

正則化參數是影響SPA分解結果的唯一參數，因此，的選取極其重要。目前，都是根據經驗選取，因此不具有普適性，且嚴重影響SPA分解的結果。基于此，文中以多尺度樣本熵均值和偏度的平方作為適應度函數，結合GWO算法對參數進行尋優。尋優結果如表1所示。

表1 參數λ尋優結果

將尋優后的參數代入SPA中分別對往復壓縮機氣閥的4種狀態振動信號進行分析。以閥少彈簧狀態信號數據為例，經優化后的SPA方法分解后的振動信號如圖7所示。

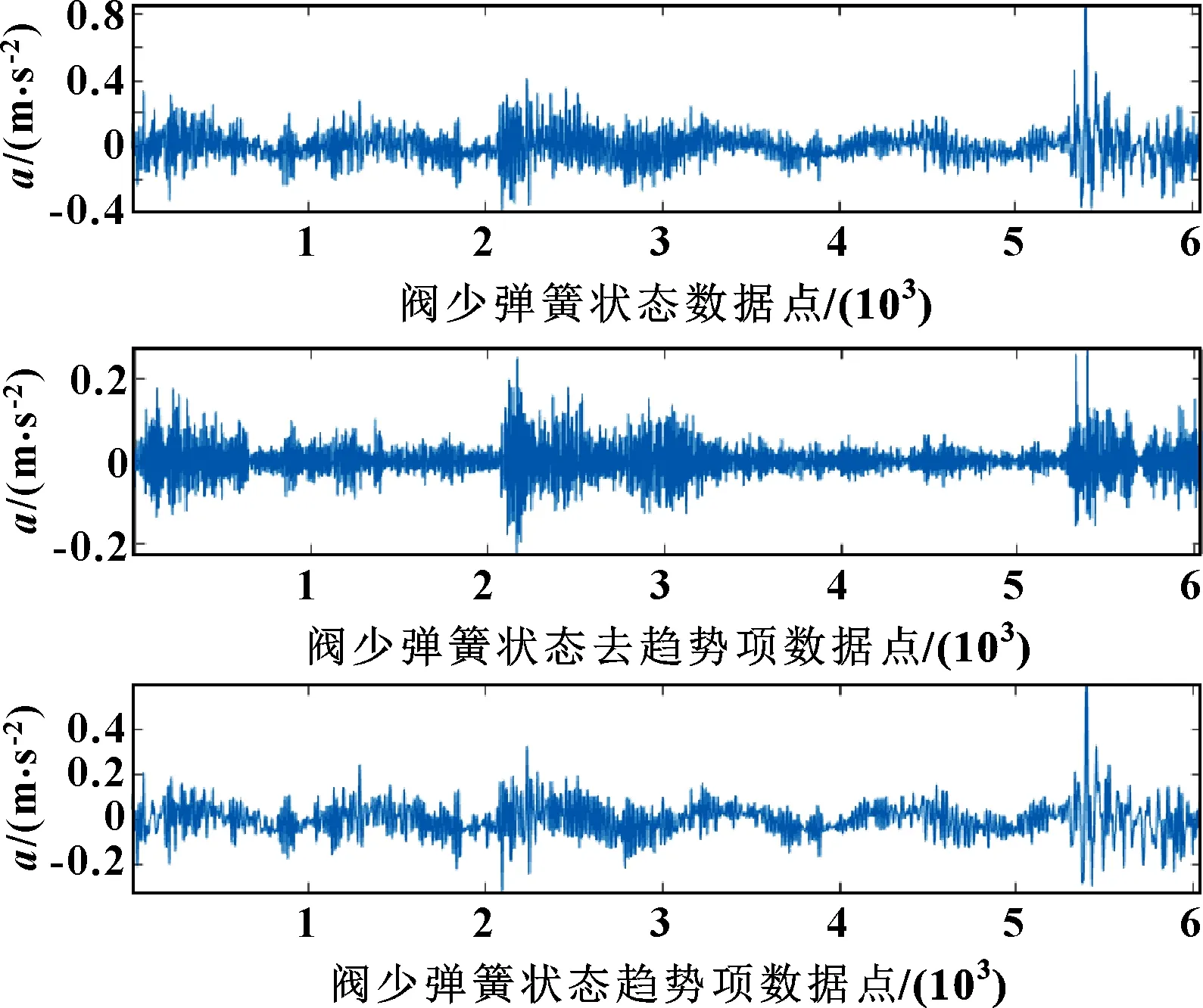
圖7 GWO-SPA分解結果

由圖7可知：信號在經過GWO-SPA分解后，可分解為趨勢項和去趨勢項兩項，因此避免了因分量選取問題對分解結果的影響。同時可以看出分解后得到的2個分量信號有明顯的區分。基于上述分析，文中研究氣閥故障時選取去趨勢項數據進行分析。

對氣閥4種狀態下分解后的去趨勢項數據分別求解MSE熵值的均值以及MSE熵值偏度的平方，MSE熵值主要受到嵌入維數和尺度因子的影響，需要選擇合理的區間，分別求取氣閥4種狀態信號下各一組數據在不同嵌入維數和尺度因子下的MSE熵值的均值，來確定和的取值，結果如圖8和圖9所示。

由圖8可以看出：嵌入維數在1—3之間氣閥的4種狀態有較為穩定且明顯的區分，因此文中嵌入維數選擇2；同時，從圖9可以看出：尺度因子大于10時氣閥4種狀態有明顯且穩定的區分，尤其在為12時，區分最為明顯，因此文中選擇為12。

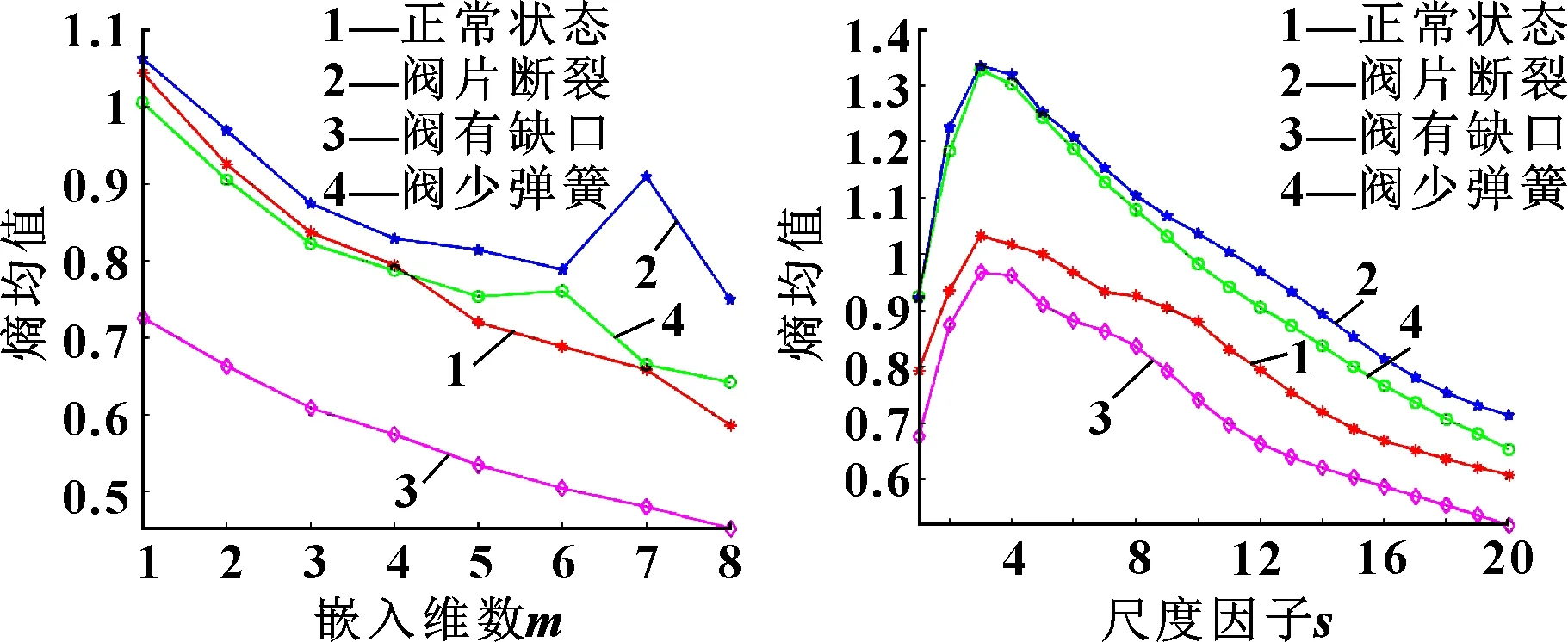
圖8 不同嵌入維數下的MSE熵值均值 圖9 不同尺度因子下的MSE熵值均值

利用上述選擇的嵌入維數和尺度因子分別對氣閥4種狀態下的去趨勢項數據求解MSE熵值均值和偏度的平方，求解結果如圖10和圖11所示。

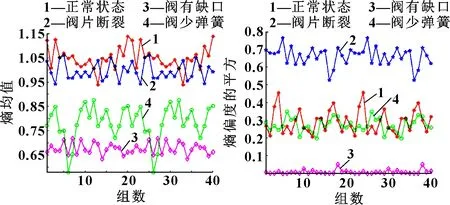
圖10 去趨勢項的MSE熵值的均值 圖11 去趨勢項的MSE熵值偏度的平方

由圖10可以看出：對往復壓縮機氣閥4種狀態的信號去趨勢項數據分別求解MSE熵值均值后，閥有缺口狀態的MSE熵值均值和閥少彈簧狀態的MSE熵值均值有稍微重合折疊現象，正常狀態MSE熵值均值和閥片斷裂狀態MSE熵值均值有嚴重重合現象。由圖11可以看出：對往復壓縮機氣閥4種狀態的信號去趨勢項數據分別求解MSE熵值偏度的平方后，除正常狀態和閥少彈簧狀態MSE熵值偏度的平方有重合現象之外，4種狀態下的MSE熵值偏度的平方有明顯的區分。因此，將MSE熵值均值作為特征向量1，記為MSE,同時將MSE熵值偏度的平方作為特征向量2，記為MSE，將MSE和MSE組合構成往復壓縮機氣閥信號的特征向量。同時設置標簽1[(MSE,MSE)]對應往復壓縮機氣閥正常狀態,標簽2[(MSE,MSE)]對應往復壓縮機氣閥閥片斷裂故障狀態，標簽3[(MSE,MSE)]對應往復壓縮機氣閥閥有缺口故障狀態，標簽4[(MSE,MSE)]對應往復壓縮機氣閥閥少彈簧故障狀態。將特征向量及標簽輸入SVM中進行分類。

在故障診斷分類中，選取往復壓縮機氣閥4種狀態下各40組數據中的24組作為訓練數據集(60%)，另外16組作為測試數據集(40%)。選擇4種狀態各8組數據組成含有32組數據的測試集，來驗證文中所提出的故障特征提取方法的有效性。其中圖12為基于SPA-MSE方法SVM診斷結果，圖13為基于GWO-SPA-MSE方法的SVM診斷結果，并將基于SPA-MSE方法和基于GWO-SPA-MSE方法的SVM診斷結果列于表2中進行對比分析。

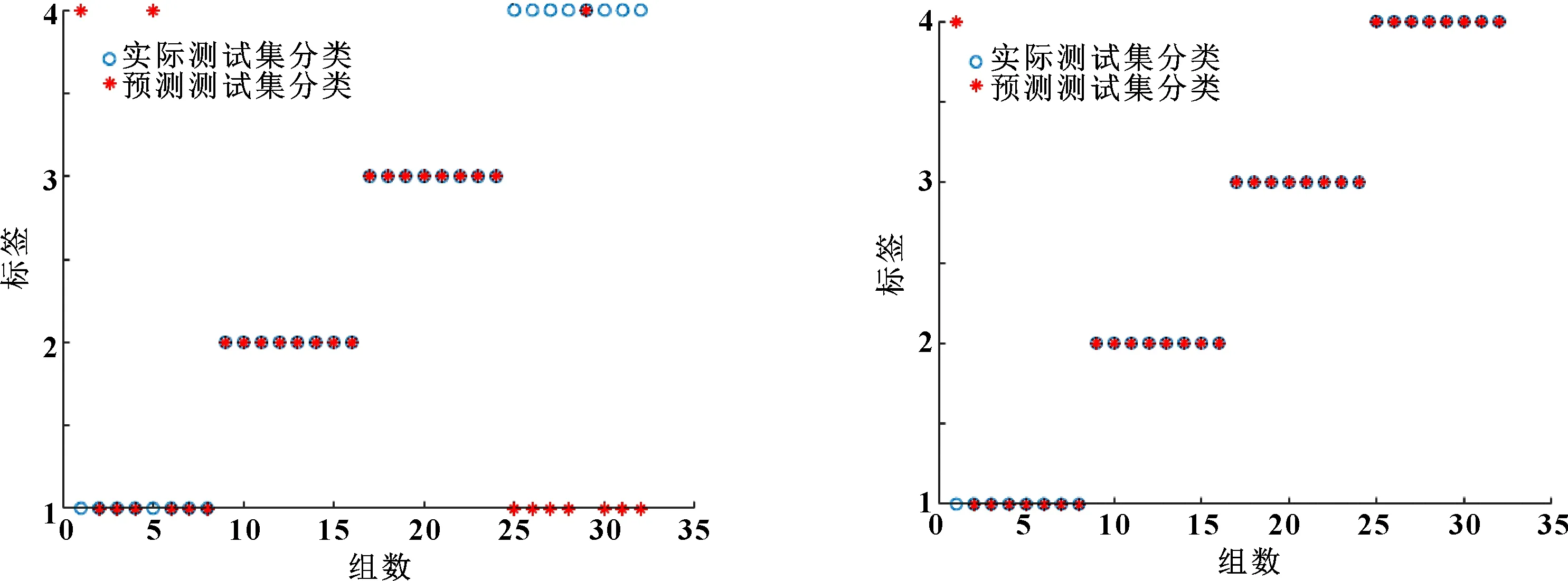
圖12 基于SPA-MSE方法SVM診斷結果 圖13 基于GWO-SPA-MSE方法SVM診斷結果

根據圖12和圖13可以看出：未對SPA進行優化前，氣閥正常狀態(標簽1)和氣閥閥少彈簧狀態(標簽4)的數據信號出現嚴重混合現象，2種狀態不能得到有效區分；對SPA進行優化后，除氣閥正常狀態有1組數據被錯誤地識別為氣閥閥少彈簧外，氣閥4種狀態信號均得到了準確的識別。從表2中可以看出：未對SPA進行優化前，盡管閥片斷裂和閥有缺口狀態數據點達到100%識別率，但正常狀態數據點只有75%識別率，閥少彈簧狀態數據點更是只有12.5%的識別率，導致SVM分類總的診斷識別率只有71.875%；對SPA方法進行優化后，正常狀態數據點識別率達到了87.5%，氣閥其他3種狀態識別率均達到了100%，總診斷識別率達到了96.875%，證明了文中所提方法的有效性和準確性。

表2 氣閥狀態診斷識別結果

4 結論

文中所提出的基于GWO-SPA和MSE的往復壓縮機氣閥故障特征提取方法，經實驗研究，可以得出以下結論：

(1)針對SPA參數選取的問題，文中對SPA方法進行了改進，提出基于GWO-SPA的信號分解方法，并成功應用于往復壓縮機氣閥信號特征提取中。

(2)對優化后的SPA分解得到的去趨勢項數據分別求解MSE熵值的均值和偏度的平方，并將其結合構成往復壓縮機氣閥特征向量，可以全面且定量地反映出氣閥振動信號的特征，從而對往復壓縮機氣閥不同狀態下的信號特征進行有效的提取。

(3)通過實驗分析及與未優化之前的SPA-MSE方法進行對比可知，文中所提出的故障特征提取方法，對往復壓縮機氣閥信號總故障識別率達到96.875%，驗證了文中所提方法的有效性和準確性。