小物和小理的物理對話錄(98)
——圖像問題分析

黃碧涵 何 龍 孟衛東(正高級教師)

(清華大學附屬中學永豐學校)

前言:小物和小理是2名普通的高中生,他們酷愛物理,在學習物理的過程中,小物經常向小理提出許多刁鉆而有趣的物理問題,了解他們的故事也能讓你的物理達到新的高度.

1 對話錄

小物:小理,可算找到你了!

小理:怎么了? 什么事兒這么著急?

小物:小理,最近我們學到運動學部分內容,常常涉及圖像,我總是分析得不對.

小理:我覺得圖像題并不難呀! 厘清各物理量間的關系和圖像斜率、截距等代表的物理意義就能順利解題了.

小物:解答物理問題難道還要畫圖,求斜率,求截距?

小理:那我得批評一下你的態度了,我們學習的目的就是解釋我們看到的現象,在研究問題時,不同的學科知識都要利用起來.

小物:你說得對……

小理:高中物理應該用邏輯思維去分析問題,我們剛剛學完運動學的基本概念,可以基于這些基本的物理概念來分析問題.高中物理中的速度、加速度、位移等都具有矢量性,都涉及方向.我們就剛學習的勻變速直線運動的相關知識點,從圖像的角度一起來討論一下吧!

2 小理的解釋

2.1 速度與加速度矢量分析

針對圖1的勻變速直線運動圖像,我們建立一維的物理模型.

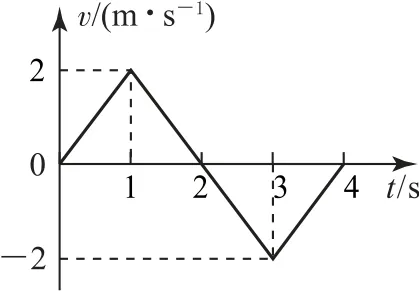
圖1 勻變速直線運動圖像

汽車從靜止開始啟動,設向右為正方向,從圖像可以看出,在0～2s時間內,速度始終為正,也就是說這段時間速度的方向始終與規定的正方向相同.

而2～4s時間內速度始終為負,說明速度方向與規定的正方向相反,方向向左.

我們再來看汽車在0～1s時間內的加速度特點,根據圖線趨勢,結合數學中的一元一次方程y＝kx＋b,可知k＞0,b＝0;而我們知道速度—時間圖像的斜率表示加速度,因而加速度a＝k＞0,為正值,方向向右.同樣地,在1～2s時間內,根據圖線趨勢,結合數學中的一元一次方程y＝kx＋b,知k＜0;說明這段時間加速度a＝k＜0,為負值,方向向左.同理可分析出,2～3s時間內的加速度a＜0,方向向左;3～4s時間內的加速度a＞0,方向向右.通過圖像可進一步求出加速度的大小始終為

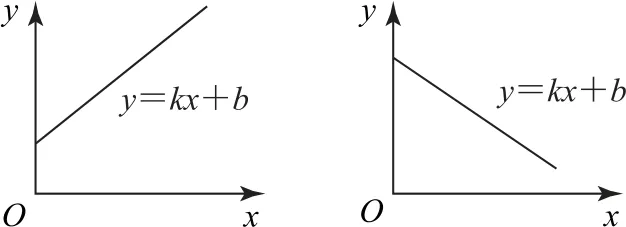
圖2 數學中的一元一次方程圖像

當加速度方向與速度方向相同時,汽車做加速運動;當加速度方向與速度方向相反時,汽車做減速運動.因而汽車在0～2s時間內的運動規律為:從靜止開始,在0～1s時間內做向右的勻加速直線運動,加速度大小為2m·s－2,1s的末速度為2 m·s－1;汽車在1～2s時間內做向右的勻減速直線運動,加速度大小為2m·s－2,速度最終減為0.汽車在2～4s時間內的運動規律為:汽車從初速度為0開始,在2～3s時間內做向左的勻加速直線運動,加速度大小為2 m·s－2,3s的末速度為2m·s－1;汽車在3～4s時間內做向左的勻減速直線運動,加速度大小為2m·s－2,速度最終減為0.速度和加速度的方向如表1所示.

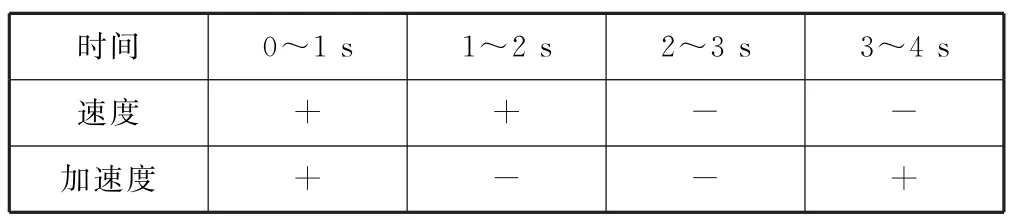
表1 速度和加速度的方向

汽車的運動方向,也就是速度方向發生改變的時刻是在2s末.從圖像上看,隨著時間的變化,對于0～2s和2～4s兩段時間,物體的運動過程具有對稱性,速度和加速度的變化規律是一致的.因而,在運動學問題中,我們可用速度—時間二維圖像來描述物體一維運動的矢量性運動特征,正負號就表示矢量的特征.對于物體的二維及三維運動,我們也可以用圖像進行描述.

2.2 “降維”分析復雜運動

物體的直線運動是在一維層面上,而物體的曲線運動要從二維層面,即在平面直角坐標系中進行研究.我們知道物體做曲線運動的條件是合力(加速度)與速度方向不在同一條直線上,比如平拋運動.研究平拋運動時,常利用化曲為直的思想,把復雜的二維運動轉化為一維運動,即把平拋運動分解成水平方向的勻速直線運動和豎直方向的勻加速直線運動.根據上文對物體一維運動的圖像分析思路,這里可將圖3合成后的二維曲線運動分解為物體在水平方向上的初速度為0、加速度大小為1 m·s－2的勻加速直線運動,以及豎直方向上的速度為2 m·s－1的勻速直線運動.

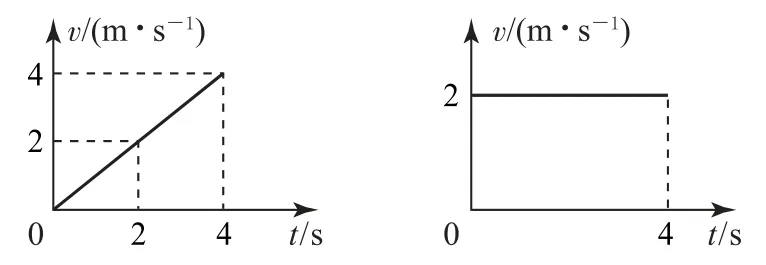
圖3

同樣,曲線運動中的圓周運動也是二維運動.研究勻速圓周運動時通常是將其分解成沿半徑方向和沿切線方向的兩個一維運動:沿切線方向為勻速運動,而沿半徑方向存在加速度大小不變的且始終指向圓心的運動;對于變速圓周運動可以分解為:沿切線方向的加速或減速運動,沿半徑方向為指向圓心的加速運動.電學中,沿垂直電場方向射入且初速度為v0的帶電粒子(重力不計)在電場中做類平拋運動,可分解為垂直電場方向的勻速直線運動(vx＝v0)和沿電場方向的勻加速直線運動.上述二維運動的一維分運動均可用速度—時間圖像來表示.

更進一步,對于空間中的三維運動,如圖4所示,垂直于Oxz平面且軌跡像螺紋一樣勻速旋轉前進的物體,可將其運動分解為沿z軸方向的一維直線運動及沿Oxy面的二維平面圓周運動,如帶電粒子在復合場中,在洛倫茲力的作用下粒子做勻速圓周運動,而在電場中粒子可做v0＝0的勻加速直線運動.

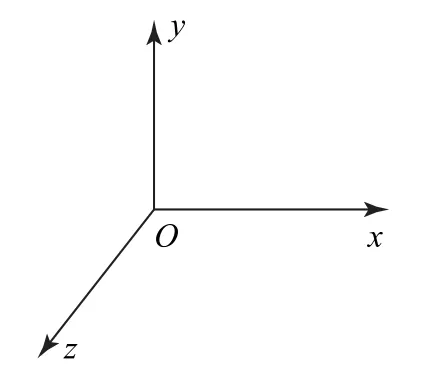
圖4

因此,在描述物體的運動過程時,物體的速度、加速度、位移等物理量都是矢量,和力一樣,都可以進行矢量分解,遵循平行四邊形定則.在處理較為復雜的運動學問題時,都可以利用“降維”的物理方法去分析,實現化復雜為簡單的目標.

3 小物的感悟

聽你講完,我發現原來運動學中的圖像問題并不難,即使是研究較為復雜的二維或三維運動問題時,圖像也可以起到化繁為簡的作用.在以后的物理學習中我會多總結物理思想和方法,深入思考物理知識背后的物理規律,相信在未來的物理學習中一定會取得更大的進步.

(完)