基于季節-WNN組合模型的煤礦事故預測

郭進平，周國悅，晏承園

(西安建筑科技大學資源工程學院，陜西 西安 710055)

實現經濟增長與保證安全生產是我國國民經濟建設面臨的兩大根本性問題[1]。通過現有安全狀況預測未來安全演化趨勢，在預測結果的基礎上合理有效加強各方面建設，提高本質安全水平，是實現安全生產的有效途徑[2-3]。很多學者在安全預測方面已做了大量研究，原始時間序列的安全預測模型方面，一些學者提出了基于偏最小二乘回歸法、灰色系統法、馬爾可夫鏈法、貝葉斯法等傳統的預測模型及其組合模型[4-8]，以挖掘導致事故的高頻因素組合及事故突出程度與因素之間的關系。但傳統預測模型難以找出系統多元因素與生產事故的非線性交互關系，不能提取對安全預測有利的因素，預測效果不佳。為了提高安全預測精度，有學者提出基于數據分解技術的安全組合預測模型。范忠洲等[9]以全國水上交通事故數據作為樣本，建立了灰色BP神經網絡組合預測模型，提高了水上交通事故數的預測精度。WU等[10]利用經驗模態分解法(EMD)將非平穩原始時間序列分解為高頻信號和低頻信號，用GM模型預測高頻信號序列，用ARMA模型預測低頻信號序列，通過疊加各子序列的預測結果，構建了EMD-GM-ARMA模型，為礦山安全生產狀況提供高精度、高穩定性的預測。梁文娟等[11]通過建立差分自回歸移動平均模型(ARIMA)、最小二乘支持向量機模型(LS-SVM)和BP神經網絡模型(BPNN)的組合模型，對某航空公司運輸的月度飛行事故進行了預測分析。這類組合預測的方法雖在一定程度上解決了安全時間序列高復雜度的問題，提高了預測精度，但這類方法較多考慮了安全事故發生的離散性和偶然性[12]。事實上，生產領域安全狀況受復雜的自然因素和社會因素共同作用影響，存在明顯的季節性特征。韓國旭等[13]通過收集陜西省生產安全月度死亡人數數據，發現其具有明顯的季節性特征，建立了基于季節性因素的灰色時序模型。袁婧[14]分析施工中存在季節性因素，提出應對特殊情況的應急準備，并展開有效分析，從而為保障工程施工安全和質量提供依據。目前，季節性事故逐漸呈多發趨勢，表現出概率高、突發性強、預防難度大的特點，但目前對于這方面的研究并不深入。

本文以我國2015—2020年的煤礦事故死亡人數的月度數據為樣本，考慮安全生產過程中的季節效應，通過X-12-ARIMA模型進行季節調整，將事故死亡人數的時間序列分解為平穩時間序列和季節因子序列，季節因子序列每年呈現相同規律，基于小波神經網絡(wavelet neural network，WNN)模型對平穩時間序列進行預測。并對比分析當前幾種比較典型的預測模型的預測結果，驗證季節-WNN組合預測模型的預測精度，以此反映出煤礦生產事故發生的季節性特征，達到良好的預測效果，從而為我國煤礦生產事故的預測提供一種思路。

1 季節-WNN組合模型

1.1 季節調整

季節調整是指對原始月度或季度時間序列中隱含的季節性因素影響進行修正或消除的過程[15]，季節調整可以通過X-12-ARIMA模型來實現，采用Eviews軟件實現編制程序對時間序列進行季節調整，其過程可分為建模、季節調整和診斷三個階段[16]，如圖1所示。

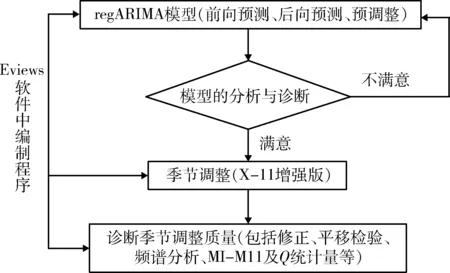
圖1 X-12-ARIMA模型結構圖Fig.1 Structure drawing of X-12-ARIMA model

1.2 小波神經網絡

小波神經網絡(WNN)模型的結合方式一般有兩種：一種是輔助型結合，另一種是緊密型結合[17-18]。 本文采用緊密型WNN模型，其學習算法為梯度下降法，共有三層，分別為輸入層、隱含層和輸出層。 拓撲結構如圖2所示，其中，X1，X2，…，Xt為WNN模型的輸入參數，H1，H2，…，Hj為隱含層傳遞函數，Y1，Y2，…，Yk為輸入值經網絡傳輸后的相應輸出值，wij和wjk為網絡各層之間的連接權值。

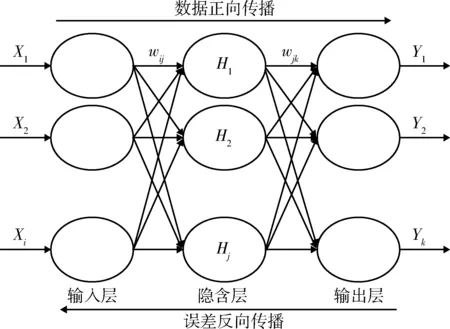
圖2 WNN模型結構圖Fig.2 Structure diagram of WNN model

1.3 季節-WNN組合模型原理

運用組合預測法[19]將X-12-ARIMA模型與WNN模型進行綜合，組建出一種季節-WNN組合模型，其建模步驟如圖3所示。

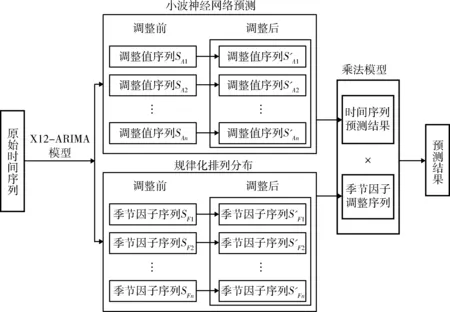
圖3 季節-WNN組合預測建模原理Fig.3 Modeling principle of seasonal-WNN combined prediction

1) 將原始數據的時間序列按時間順序排列成一組隨機變量，記為{Xt,t=1,2,…,N}，N代表時間的集合。用X-12-ARIMA模型進行分解，得到一個季節調整值序列SA和一個季節因子序列SF，關系式見式(1)和式(2)。

SA=TtIR

(1)

式中:Tt為長期趨勢序列；IR為不規則變動因素序列。

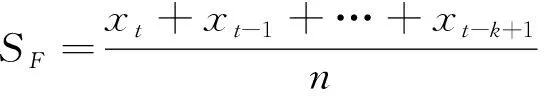
(2)

式中：n為時間序列的滑動平均項數；k為季節周期，若k=4，則表示時間序列為季度數據，若k=12，則表示時間序列為月度數據[20]。

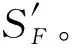
3) WNN模型參數權值修正及訓練步驟如下所述。

步驟1：設置輸入層與隱含層的連接權重值wij，得到隱含層輸入參數hj，見式(3)。

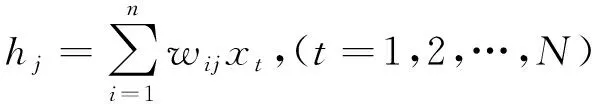
(3)

長期趨勢序列Tt與時間t的關系式見式(4)。

Tt=a+bt

(4)

式中：a為平移因子；b為伸縮因子。

由此，調整小波基函數的平移因子a與伸縮因子b，得到隱含層輸出參數Hj見式(5)。

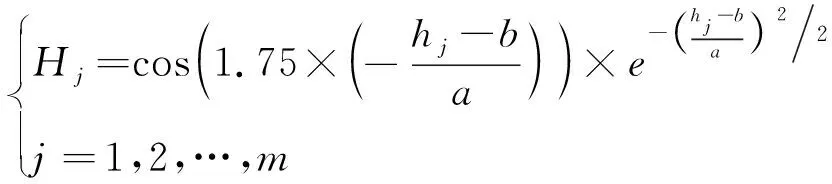
(5)

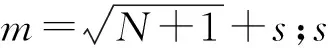
步驟2：設置隱含層與輸出層的連接權重值wjk，得到最終的輸出層輸出參數Yk表達式見式(6)。

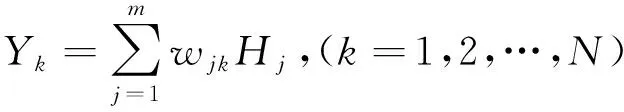
(6)

在控制過程中，實時以WNN模型輸出預測值與真實值的差值為依據對WNN模型進行誤差分析。通過使預測輸出不斷接近實際數值，提高預測精度來進行權值修正。 相應的誤差函數E見式(7)。

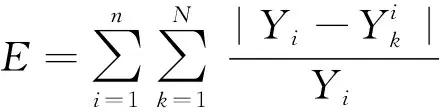
(7)

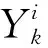
根據得到的誤差E來修正網絡連接權重值wij、wjk及平移因子a與伸縮因子b。參數修正公式見式(8)～式(11)。

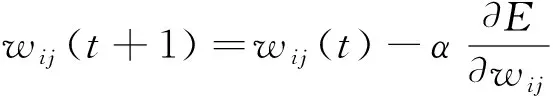
(8)

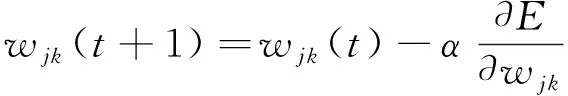
(9)

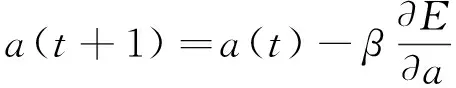
(10)

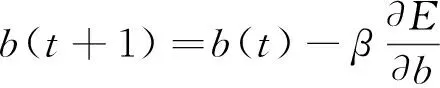
(11)

式中，α和β分別為wij、wjk和a、b的學習速率。

4) 對WNN模型參數權值修正及訓練步驟進行判斷，誤差達到最小時則結束預測，否則返回重新計算，直到達到預測精度為止。

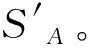
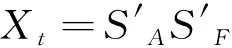
(12)

經過X-12-ARIMA模型進行季節優化調整，再通過WNN預測模型研究，比較各分量的周期變化規律，可以充分揭示出時間序列的結構，掌握其主要的波動特征，以此分析季節因素對安全事故的影響。而且，建立的季節-WNN組合預測模型在研究這種季節因素影響下時間序列的周期波動方面，可有效對數據中的噪聲擾動進行排除，具有單一時序方法所無法企及的優勢[21]。

2 實例應用

2.1 樣本數據來源

本文研究數據來源于國家統計局每年公布的我國煤礦事故死亡人數。由于季節調整模型要求數據必須為月度數據或季度數據，為保證分析結果的準確性和時效性，以2015—2020年每個月的死亡人數作為原始數據樣本。將原數據分為兩部分：2015年1月—2019年12月的數據用作訓練集以構建模型；2020年1月—2020年12月的數據作為測試集來驗證模型的預測精度。

表1為2015年1月—2020年12月我國煤礦事故死亡人數的月度數據。由表1可知，事故頻發時段多在秋季，死亡人數最多的月份在每年11月；冬季12月份較多，死亡人數最少的月份在每年2月；春季在3月—4月返工時期，事故頻發；夏季整體事故數量偏少，月平均死亡人數低于30人，煤礦事故死亡人數整體呈現較為明顯的季節性特征。需要注意的是，2020年1月—5月受新冠疫情影響，大多數煤礦企業相繼停工停產，煤礦事故每月死亡人數明顯低于以往年份。隨著疫情得到控制，從2020年6月起煤礦逐漸恢復生產，死亡人數又逐漸增多，繼而呈現出與以往相同的季節性特征。

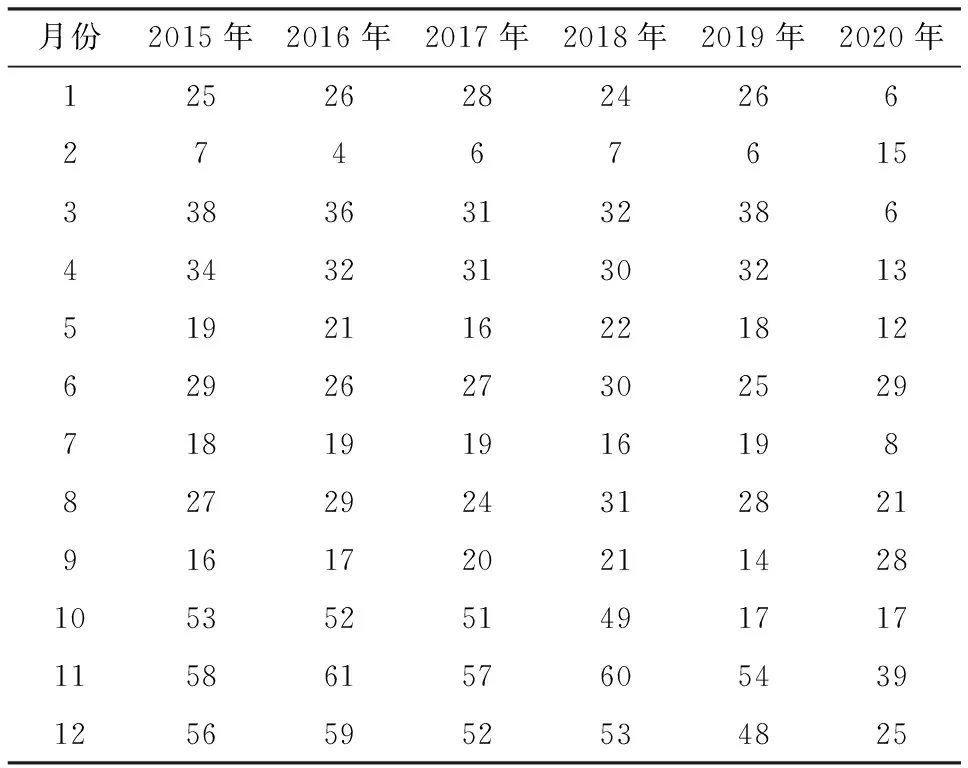
表1 2015—2020年全國煤礦事故死亡人數月度數據Table 1 Monthly coal mine fatalities from 2015 to 2020 單位：人

2.2 季節性校驗

根據煤礦事故死亡人數的季節性特征，對其原始數據進行識別，得到全國煤礦事故死亡人數的原始時間序列，如圖4所示，其中，橫坐標代表時間軸，縱坐標代表死亡人數波動情況。

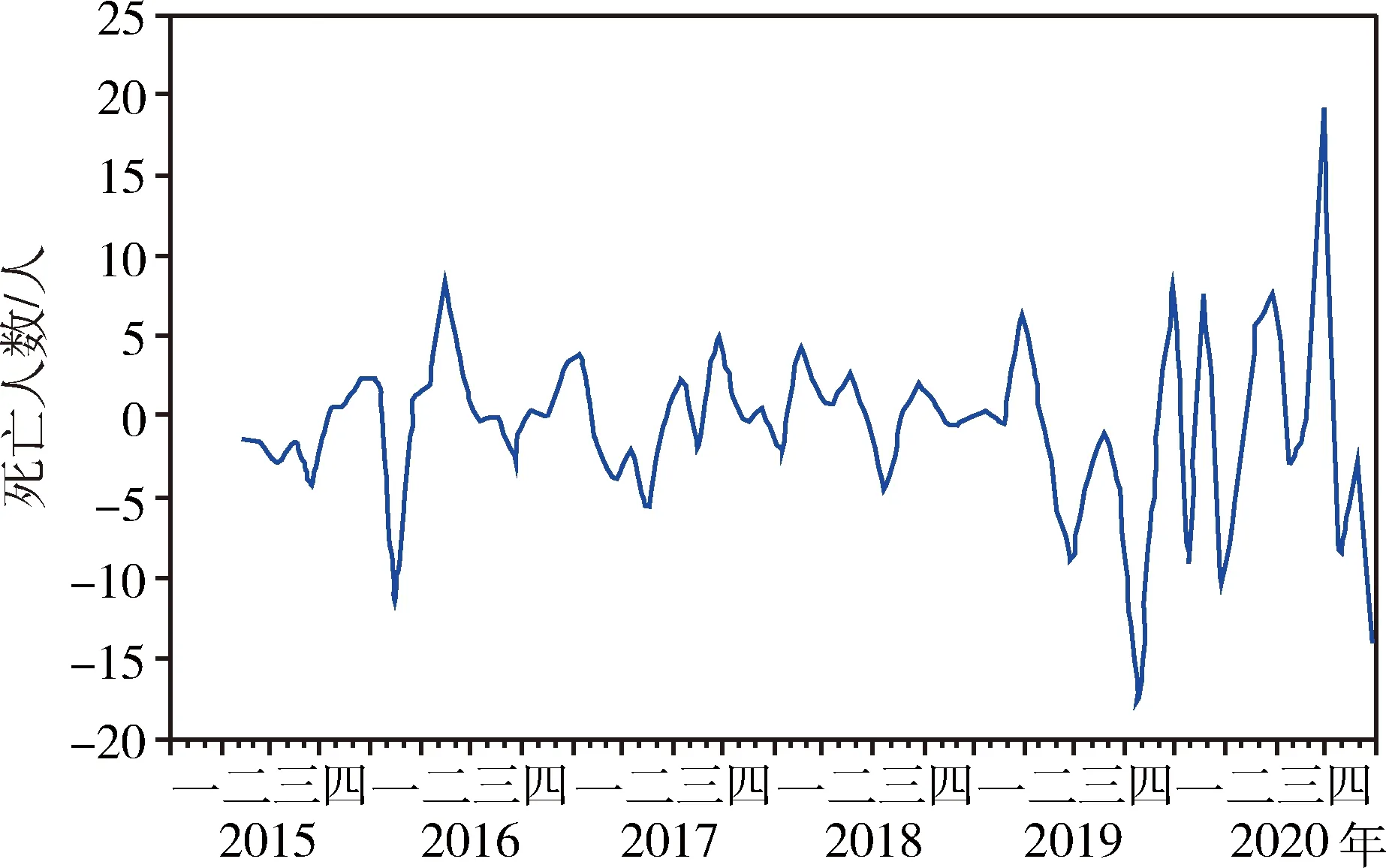
圖4 2015—2020年全國煤礦事故死亡人數原始時間序列圖Fig.4 Raw time series chart of coal mine fatalitiesin China from 2015 to 2020

對2015—2020年全國煤礦事故死亡人數時間序列進行自相關分析，結果見圖5。由圖5可知，顯著性水平(Prob)小于0.05，這說明煤礦事故死亡人數時間序列與季節性因素顯著相關，即存在明顯的季節性特征。

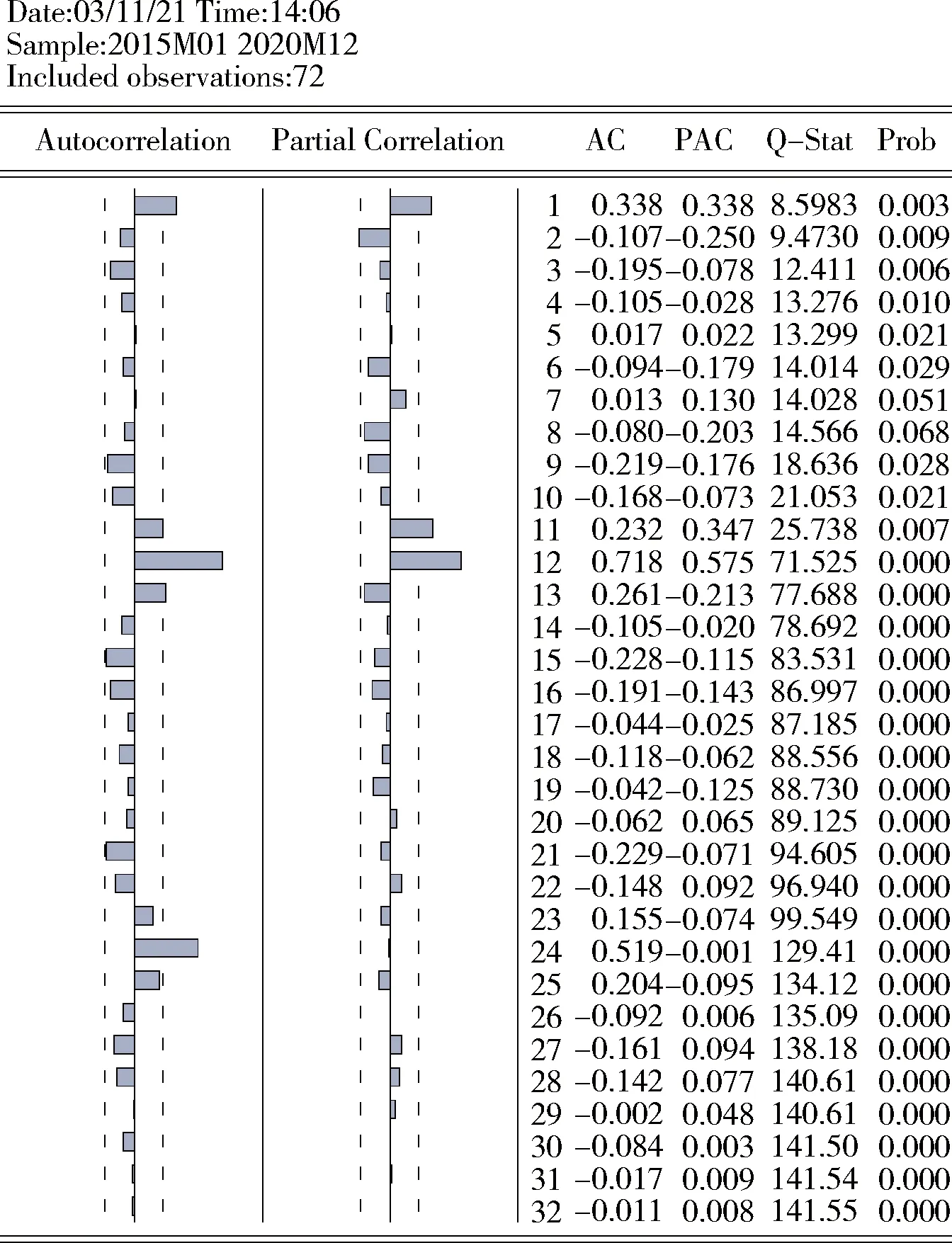
圖5 月度死亡人數時間序列自相關檢驗圖Fig.5 Auto-correlation test chart of time seriesof monthly deaths

運用X-12-ARIMA模型對煤礦事故死亡人數時間序列進行季節調整，得到季節調整時間序列圖(圖6)。由圖6(a)可知，季節因子存在周期性變動，每年的第一季度為事故發生最低峰，第四季度為事故發生最高峰。這可能是由于季節變換致使作業環境變化或受春節前后產能調整的影響，員工心理或生理發生微妙變化，容易引起安全事故，導致每年的第四季度事故頻發，并以此為時間節點引起季節性周期波動。由圖6(b)可知，不規則變動影響因素呈現一種無規律可循的變動，可能包括心理生理影響、氣候變化等偶然性因素。由圖6(c)可知，剔除季節因素后的時間序列呈現波動特征，此過程時間序列仍處于非平穩狀態，還無法進行控制及預測。由圖6(d)可知，煤礦事故死亡人數長期波動情況總體呈現非線性降低趨勢。

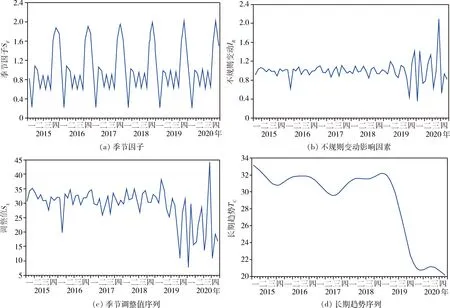
圖6 季節調整時間序列圖Fig.6 Seasonal adjusted time series diagram

在完成季節調整后，對季節調整值SA進行假設檢驗。圖7為季節調整值SA的假設檢驗結果，可以看出t-Statistic等于-8.989 022，均小于1%、5%、10%水平下t-Statistic的值，拒絕原假設，認為SA沒有單位根，且顯著性水平(Prob)小于0.001，說明被調整后的季節調整值時間序列是平穩的。

圖7 季節調整值SA檢驗結果Fig.7 Test results of seasonal adjusted values SA

2.3 季節-WNN組合預測模型可靠性分析

將季節調整值序列小波預測后，按乘法模型與季節因子序列組合得到新的預測時間序列，獲取煤礦事故死亡人數的預測結果如圖8所示。

由圖8可知，單一的WNN模型的預測值與煤礦事故死亡人數真實值相差較大，平均相對誤差約為19.62%。 進行季節調整之后，結合WNN模型建立的組合預測模型，通過對2015年1月—2019年12月之間全國煤礦事故死亡人數進行學習訓練，發現其訓練值與真實值基本一致，均方誤差僅為1.86%。對2020年煤礦月度死亡人數進行預測，發現季節-WNN組合模型的預測值與真實值基本吻合，平均相對誤差也只有1.11%，說明在考慮安全生產的季節效應后可有效提高安全預測的精度，達到良好的預測效果。

圖8 季節-WNN組合預測模型趨勢圖Fig.8 Trend chart of seasonal-WNN combinedprediction model

2.4 多種預測模型對比分析

選用灰色系統模型、BP神經網絡模型等對2019—2020年數據進行預測分析，通過對各個預測模型的誤差和穩定性進行分析，分別計算出預測模型相應的平均絕對差值(MAD)、平均相對誤差(MAPE)、均方誤差(MAE)、均方根誤差(RMSE)，結果見表2。

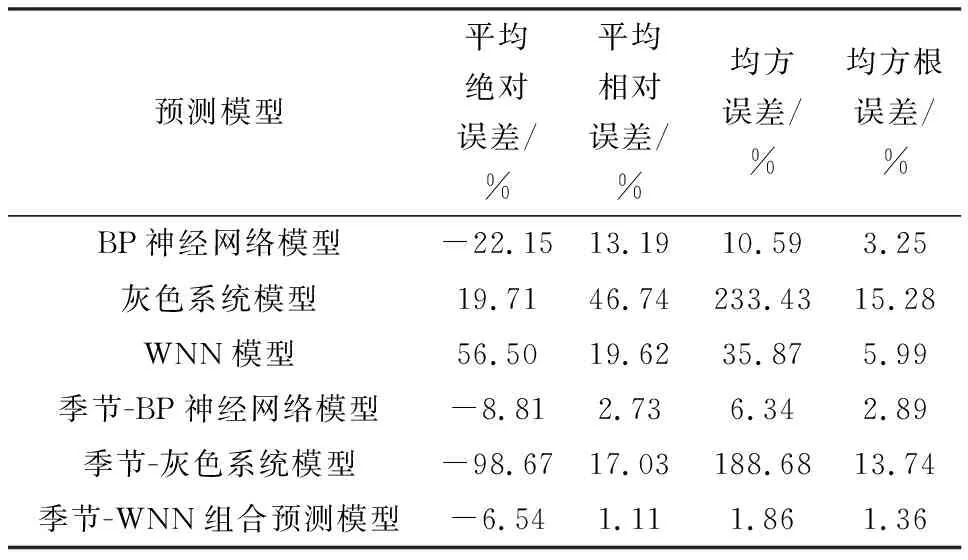
表2 各模型預測精度檢驗結果Table 2 Test results of prediction accuracy of each model

為了更形象直觀地突顯預測模型的預測效果，圖9和圖10分別為灰色系統模型和BP神經網絡模型與季節調整相結合的構建組合，對其預測結果進行對比分析。

圖9為灰色系統模型與季節-灰色系統組合預測模型預測圖。其中，煤礦事故死亡人數的真實值呈現波動變化；單一灰色系統模型進行預測的預測值與真實值相差甚遠，平均相對誤差為46.74%，均方誤差高達233.43%，未達到預測效果；季節調整后的灰色系統模型預測值，雖未達到預測目的，但平均相對誤差下降29.71%，均方誤差下降44.75%，精度有所提升。但相比季節-WNN組合模型，灰色系統模型與季節-灰色系統組合預測模型預測精度較低，不適合對煤礦事故死亡人數進行安全預測。

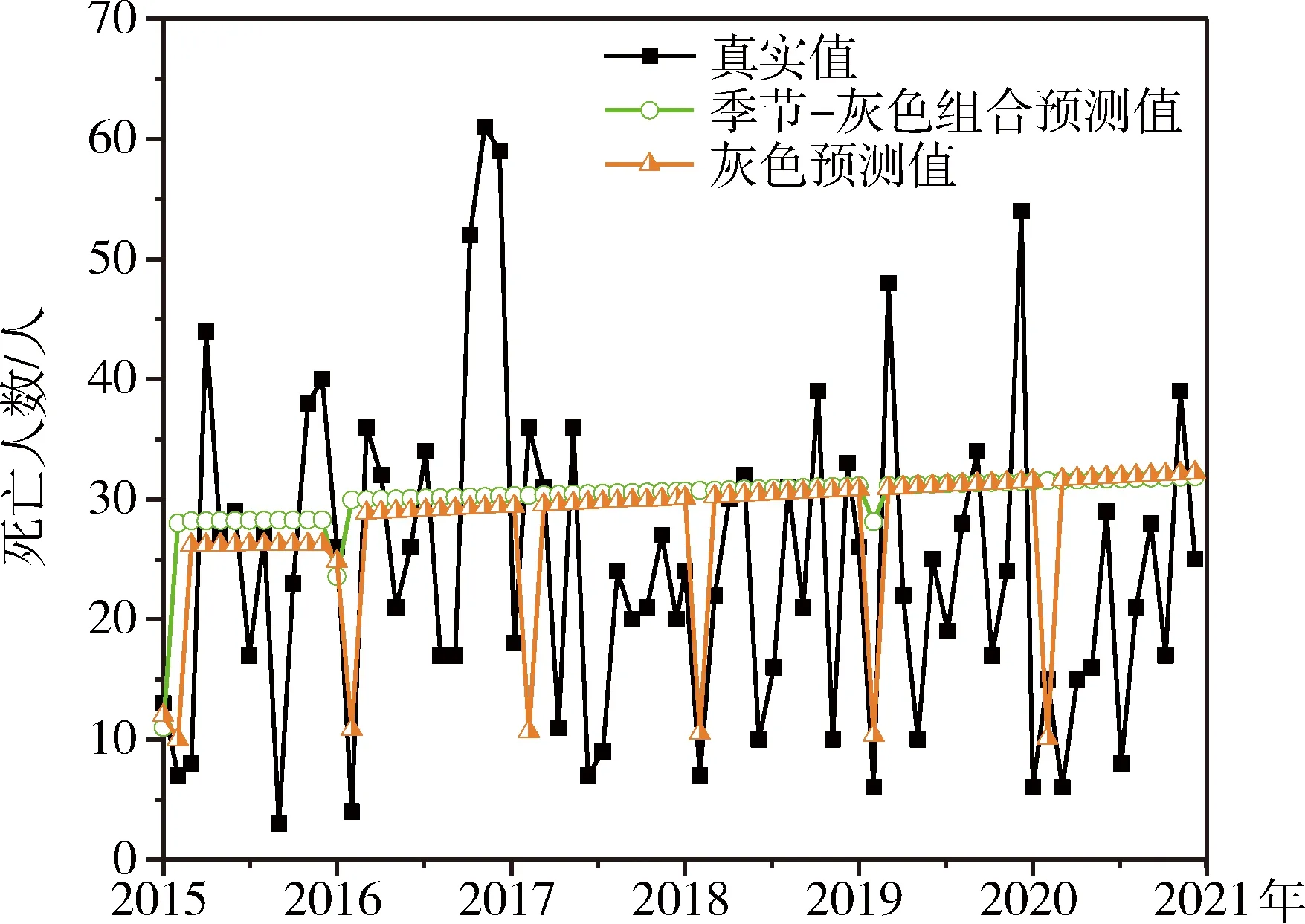
圖9 灰色系統模型與季節-灰色系統組合模型預測趨勢圖Fig.9 Forecast trend chart of grey system model andseasonal-grey system combination model

圖10為BP神經網絡模型與季節-BP神經網絡組合模型預測趨勢圖。 由圖10可知，BP神經網絡模型預測值波動幅度較大，平均相對誤差為13.19%，

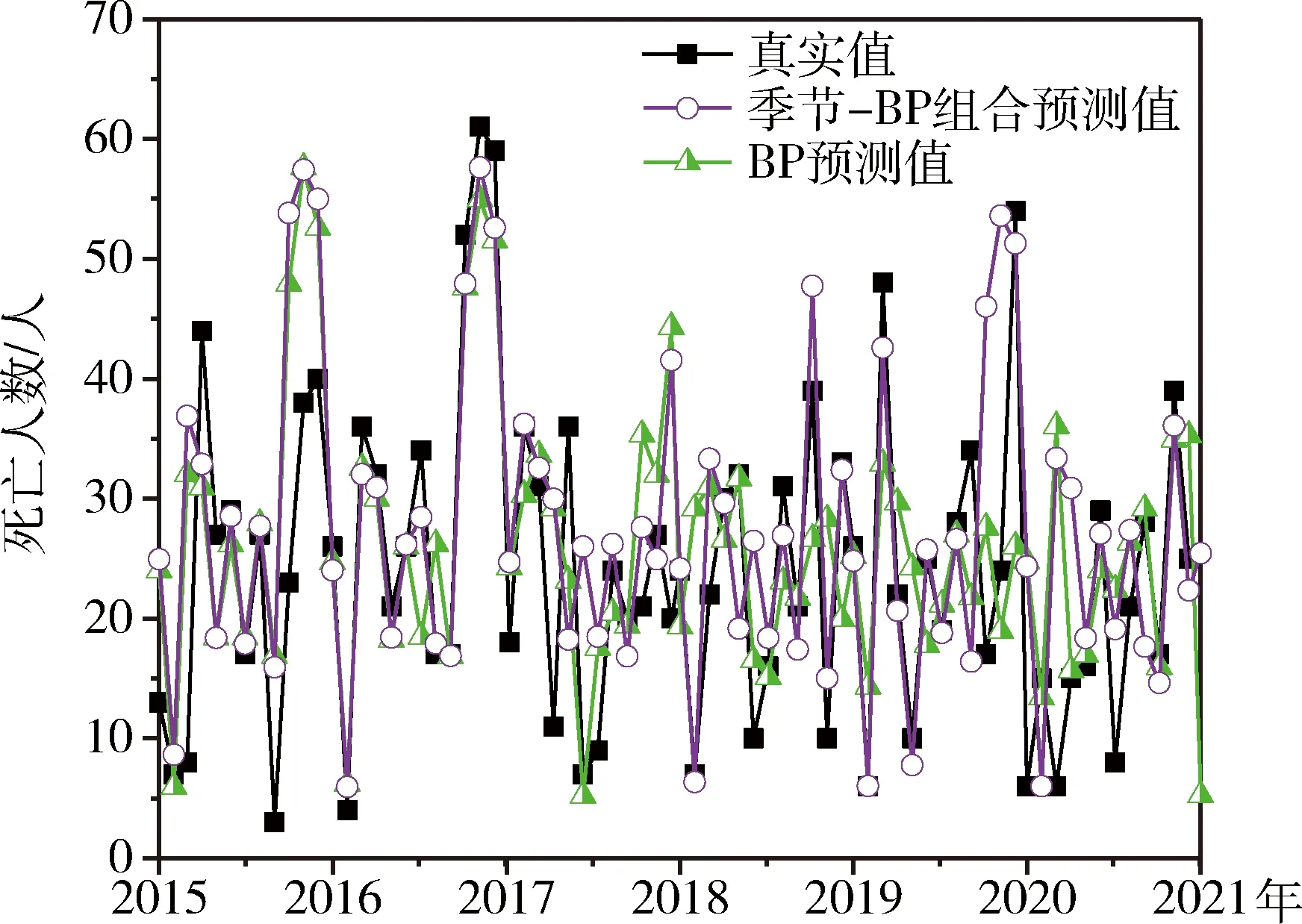
圖10 BP神經網絡模型與季節-BP神經網絡組合模型預測趨勢圖Fig.10 Prediction trend chart of BP neural network modeland seasonal-BP neural network combination model

均方誤差在10%以上，大部分預測值與真實值相差較大，預測效果較差；結合季節調整后的BP神經網絡預測模型預測值，平均相對誤差降至2.73%，均方誤差也只有6.34%，只有小部分預測值與真實值相差較大，預測結果明顯較單一，BP神經網絡模型預測更為精確。季節-BP神經網絡組合預測模型也適合對煤礦事故死亡人數進行安全預測。但相比季節-WNN組合模型，其預測精度仍有待提高。

單一的預測模型由于未排除季節波動的影響，事故死亡人數往往可能存在偶然性，且數據基數較小，因此比季節調整后的預測模型的預測誤差更大。而在經過季節調整后，這些單一的預測模型預測精度明顯都大幅提升，其中季節-WNN組合模型的整體誤差和實際偏差均比其他預測模型的精度更高。季節-WNN組合模型較好地結合了小波變換和時間序列模型的優勢，利用X-12-ARIMA模型進行季節調整得到的季節性因素和周期性特征，使得該模型對于時間序列的發展變化趨勢刻畫較為精確。此外，在季節-WNN組合模型應用過程中還發現，該組合預測模型從小樣本數據著手，進行短期預測，使得建模較為簡便，短期預測方面表現良好，能夠削減因為死亡人數隨機性和波動性引起的精度降低等問題，有著很好的應用前景。

3 結 論

1) 通過收集數據分析發現，我國煤礦事故受季節因素的影響較為明顯，將安全事故視為按時間次序排列的隨機變量序列，而任何時間序列均可通過合理的函數變換后，形成趨勢變換和季節周期變換。采用X-12-ARIMA模型對煤礦事故的原始時間序列進行季節調整，運用WNN模型進行函數變換，并將兩者相結合進行預測分析，這對于考慮安全生產的季節效應進行安全預測提供了一個新的途徑。

2) 本文所建立的季節-WNN組合模型，平均相對誤差為1.11%，均方誤差為1.86%，說明該組合預測模型預測穩定性較好，預測精度較高，且季節-WNN組合模型從小樣本數據著手，建模更為簡便，短期預測效果良好，可為煤礦安全決策提供相關理論依據。

3) 通過對我國煤礦事故死亡人數近五年的月度數據組建多模型進行預測分析，運用X-12-ARIMA模型排除季節因素對時間序列的影響，再結合不同預測模型預測的效果好于未經過季節調整的單一預測模型的預測效果。季節-WNN組合模型的預測結果比其他幾種預測模型的平均相對誤差及均方誤差更低，說明其預測精度更高，能較好地反映安全生產過程中受季節因素影響所呈現的規律性變化，有效預測復雜事故系統的發展趨勢變化。雖然該組合預測模型短期預測效果顯著，但中長期預測精度仍需深入研究。